Journal of Applied Mathematics and Physics
Vol.04 No.07(2016), Article ID:69243,10 pages
10.4236/jamp.2016.47144
Two Scenarios on the Relativistic Quantum Heat Engine
Agus Purwanto, Heru Sukamto, Bintoro Anang Subagyo, Muhammad Taufiqi
Laboratorium Fisika Teoridan Filsafat Alam, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2016; accepted 25 July 2016; published 28 July 2016
ABSTRACT
We compare two different scenarios at relativistic quantum heat engine by considering three-level energy, and two non-interacting fermion in one-dimensional potential well. The difference between the scenarios is about mechanism to get into excited state by two fermions. We apply iso-energetic cycle that consists of two iso-energetic and two iso-entropic processes, and then compute and compare the efficiency at both scenarios. We also compare it with non-relativistic case. The result is that one scenario has larger efficiency than the other that does not happen at non-relativistic case.
Keywords:
Quantum Heat Engine, Relativistic, Scenario

1. Introduction
In principle, the classic heat engine works by taking the heat from the hot reservoir and converting it into mechanical work, and throws some heat to a cold reservoir. Thus, not all the absorbed heat can be converted into mechanical work, as said by Kelvin Plank. However, we can still strive to design cycle that can convert heat energy as much as possible. In thermodynamics, there is no cycle having the efficiency greater than Carnot cycle.
Therefore, it is interesting to review the Carnot cycle in view of the quantum. The concept of quantum heat engine was introduced first by Scovil and Schultz-Dubois [1] and had grown into many types of research, with some kind of system, and working substance, such as particle in potential well [2] - [7] , harmonic oscillator [8] , and the other various systems [9] - [15] . There have been investigated the effect of minimal length on the efficiency of engine [16] . There also have been evaluated quantum heat engine with relativistic particle as working substance [17] [18] .
In this work, we used a one-dimensional box trap with three levels of energy as a system, with two Dirac Fermions as the working substance. The purpose of this study is to investigate how internal processes effect on the efficiency at relativistic quantum heat engine. The nature of this Carnot engine will be investigated in the next section, which in general is as follows. Section 2 will discuss one-dimensional box trap as the system; then Section 3 will discuss the iso-energetic cycle of the engine that limits only three energy levels there using two fermions, as well as discuss two scenarios as the possible internal processes that can happen in this cycle. At the end of the section, we compute the efficiency the system. In Section 4, we compare the previous result with non- relativistic case, and Section 5 presents the discussions and conclusions.
2. Dirac Particle in the One-Dimensional Potential Well
Consider a single particle confined to one-dimensional potential well of the form
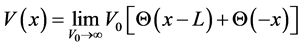 (1)
(1)
with 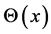 is step function. Then, Dirac equation at one dimension given by
is step function. Then, Dirac equation at one dimension given by
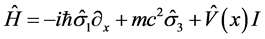 (2)
(2)
the eigenfunction as the solution of equation be expressed by
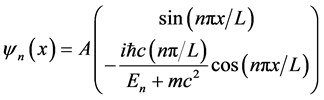 (3)
(3)
with associated energy eigenvalues
 (4)
(4)
Here,  are quantum numbers of the wave function, with
are quantum numbers of the wave function, with  is the Compton wavelength. We will not use all of the energy levels, but we only use the first three energy levels, in the meaning of simplicity, as we well show it later.
is the Compton wavelength. We will not use all of the energy levels, but we only use the first three energy levels, in the meaning of simplicity, as we well show it later.
3. Iso-Energetic Cycle of Relativistic Heat Engine
We use [2] as main reference for our quantum thermodynamics engine. It has been explained that total energy of the system analogous to internal energy and the work can be done by expanding the potential width. The isothermal and adiabatic processes at classical thermodynamics mean the same as iso-energetic and iso-entropic processes at quantum thermodynamics. We can calculate the efficiency at quantum heat engine by using the same formula as classical heat engine.
In this paper, we choose iso-energetic cycle that consists of two eno-energetic and iso-entropic process. By using two particles in a 1D box trap and three energy levels as the working substance, we get the cycle like Figure 1. We take particles at first and second level energy as the initial state A. The internal energy or total energy is given by
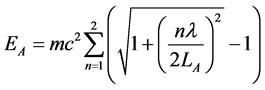 (5)
(5)
The first process is iso-energetic process. We choose the final of this process is the excited state that two particles occupying the second and third level energy. The excited state energy given by
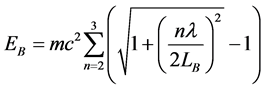 (6)
(6)
During the iso-energetic process, the internal energy is fixed. By using (5) and (6), we get relation
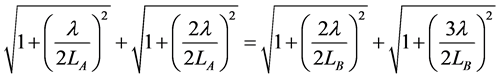 (7)
(7)
We denote 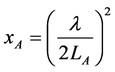 and
and , and by using a little calculation, we obtain
, and by using a little calculation, we obtain
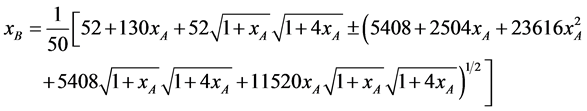 (8)
(8)
Here we obtain the width of potential well that should be fulfilled to get full excited state. But, it would be interesting if we observed this process in detail. Therefore, let us consider those fermions as distinguishable particle. At the initial state, the first particle at first level energy, and second particle at second level energy as Figure 2. We
Figure 1. Iso-energetic cycle using 2 particle at three level energy state.
Figure 2. (a) The first scenario S1, (b) the second scenario S2.
take probability for the first particle at nth-level energy as


The value of probability at initial state is given by

Then we find something interesting when we try to assign the excited state. Here we have two choices. The first choice is the first particle climbs to 2-level energy, and the second particle climbs to 3-level energy. The second choice is the first particle climbs to 3-level energy, but the second particle remains at 2-level energy. The first include both particles, the second only includes one particle. We take them as two different scenarios, S1 and S2.
3.1. The First Scenario, S1
At first scenario, probability of excitation state given by

Both particles climb to upper state. During iso-energetic process, all incoming heat becomes work. While the internal energy remain constant and satisfy

The calculation becomes simple if we calculate the change per particle separately. Therefore, we get probability relation during the process as

We also have total energy relation as

Using Equation (11), (13), (14), we get probability per particle as

As Reference [2] , probability at each level energy and quantum number change during iso-energetic process. Then, the incoming heat can be calculated as follows

The first term is for first particle, and the second term for second particle. Using (15), with a little effort we obtain

Using the result (8), we obtain the incoming heat. Then, this value turn to be work for the system

3.2. The Second Scenario, S2
Only the first particle changes its quantum number. Then the probability of excitation state given by

Probability of first particle given by

While the probability of second remains constant. The total energy given by

Then we obtain

Then, the heat exchange can be calculated as

Using (21), and little calculation, we obtain

Of course, the work during the process can be obtain by

with

The next step is iso-energetic process CD. Here we come with different scenarios again. The first scenario is both particles down to a lower energy state, first particle at second energy level move to the first energy level, and the second particle at third energy level move to second energy level. And the second scenario is the only second particle at third energy level move to the first energy level. By using (16), we obtain the heat that out of the system at first scenario, S1 by
(25)
At second scenario, S2 we obtain

The next is second iso-entropic process. As the first iso-entropic process, the work can be calculated as

After this, we calculated total work throughout a full cycle. The values of the work for both iso-entropic processes cancel each other. Then, the efficiency of the engine can be calculated for both scenarios using

It would better if the result be displayed as Figure 2.
According to Figure 3, there are difference results between S1 and S2. At S1, the efficiency increases along the increasing of the potential width. On the contrary, the efficiency at S2 decreases. While, the dependence of the efficiency with the expansion parameter can be illustrated by Figure 4 as follows.
The efficiency at S2 is lower than the efficiency at S1, and doesn’t reach unit maximum value at
4. Comparison with Non-Relativistic Case
The quantized energy at non-relativistic state given by
Figure 3. The efficiency of the engine versus the initial potential width at the first scenario S1 and second scenario S2 at
Figure 4. The efficiency of the engine versus expansion parameter first scenario S1 and second scenario S2 at

Therefore, total energy at initial condition given by

First we calculate the incoming heat at the first iso-energetic process for S1. During the process, the probability and the width of potential can be related by

Using relation (11), (15), and (16), we get the incoming heat at first scenario S1 as

Using same assumption, we can calculate the incoming heat at S2. Using relation (18), (21), and (22), we obtain

At both scenario, we got the same value,
5. Discussions and Conclusions
The differentiation of efficiency of the engine between both scenarios rises in relativistic case. This can be explained by examining the transfer energy mechanism. At first iso-energetic process, the incoming heat turns to be the work that extends the potential width as the total energy is fixed. As the consequence, the particle is excited to the upper state. At S1, both particles move to upper state to compensate the potential width extension. At S2, only particle at first energy level rises up. The particle at second energy level stays at its state while the potential width extends. This particle adsorbs the incoming heat without raising its energy level. At non-relativistic case, the value of the incoming heat has the same value at both scenarios. That means the rising of single particle at S2 can compensate the rising of two particles at S1. Both this is not happen at relativistic case. This can be explained by series expansion of relativistic energy of (4) as follows

The second term and the third term can be neglected at non-relativistic case. Whereas, at relativistic case, those terms have affected to the engine, particularly at small dimension. This can be shown by Figure 3 that at small size of initial potential width, the efficiency becomes large in S2 even still smaller than at S1.
Cite this paper
Agus Purwanto,Heru Sukamto,Bintoro Anang Subagyo,Muhammad Taufiqi, (2016) Two Scenarios on the Relativistic Quantum Heat Engine. Journal of Applied Mathematics and Physics,04,1344-1353. doi: 10.4236/jamp.2016.47144
References
- 1. Scovil, H.E.D. and Schulz-DuBois, E.O. (1959) Three-Level Masers as Heat Engines. Physical Review Letters, 2, 262.
http://dx.doi.org/10.1103/PhysRevLett.2.262 - 2. Bender, B.C.M., Brody, D.C. and Meister, B.K. (2000) Quantum Mechanical Carnot Engine. Journal of Physics A, 33, 4427-4436.
http://dx.doi.org/10.1088/0305-4470/33/24/302 - 3. Bender, B.C.M., Brody, D.C. and Meister, B.K. (2002) Entropy and Temperature of a Quantum Carnot Engine. Proceedings of the Royal Society A, 458, 1519
http://dx.doi.org/10.1098/rspa.2001.0928 - 4. Wang, J., He, J. and He, X. (2011) Performance Analysis of a Two-State Quantum Heat Engine Working with a Single-Mode Radiation. Physical Review E, 84, Article ID: 041127.
http://dx.doi.org/10.1103/PhysRevE.84.041127 - 5. Wang, J. and He, J. (2012) Optimization on a Three-Level Heat Engine Working with Two Noninteracting Fermions in a One-Dimensional Box trap. Journal of Applied Physics, 111, Article ID: 043505.
http://dx.doi.org/10.1063/1.3681295 - 6. Quan, H.T., Liu, Y., Sun, C.P. and Nori, F. (2007) Quantum Carnot Heat Engine Efficiency with Minimal Length. Physical Review E, 76, Article ID: 031105.
http://dx.doi.org/10.1103/PhysRevE.76.031105 - 7. Latifah, E. and Purwanto, A. (2011) Multiple-State Quantum Carnot Engine. Journal of Modern Physics, 2, 1366-1372.
http://dx.doi.org/10.4236/jmp.2011.211169 - 8. Arnaud, J., Chusseau, L. and Philippe, F. (2002) Carnot Cycle for an Oscillator. European Journal of Physics, 23, 489.
http://dx.doi.org/10.1088/0143-0807/23/5/306 - 9. Quan, H.T., Zhang, P. and Sun, C.P. (2006) Quantum-Classical Transition of Photon-Carnot Engine Induced by Quantum De-Coherence. Physical Review E, 73, Article ID: 036122.
http://dx.doi.org/10.1103/PhysRevE.73.036122 - 10. Scully, M.O., Zubairy, M.S., Agarwal, G.S. and Walther, H. (2003) Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence. Science, 299, 862-864.
http://dx.doi.org/10.1126/science.1078955 - 11. Scully, M.O., Chapin, K.R., Dorfman, K.E., Kim, M.B. and Svidzinsky, A. (2011) Quantum Heat Engine Power Can Be Increased by Noise-Induced Coherence. Proceedings of the National Academy of Sciences of the United States of America, 108, 15097-15100.
http://dx.doi.org/10.1073/pnas.1110234108 - 12. Quan, H.T., Zhang, P. and Sun, C.P. (2005) Quantum Heat Engine with Multilevel Quantum Systems. Physical Review E, 72, Article ID: 056110.
http://dx.doi.org/10.1103/PhysRevE.72.056110 - 13. Quan, H.T. (2009) Quantum Thermodynamic Cycles and Quantum Heat Engines. II. Physical Review E, 79, Article ID: 041129.
http://dx.doi.org/10.1103/PhysRevE.79.041129 - 14. Scully, M.O. (2002) Quantum Afterburner: Improving the Efficiency of an Ideal Heat Engine. Physical Review Letters, 88, Article ID: 050602.
http://dx.doi.org/10.1103/PhysRevLett.88.050602 - 15. Dillenschneider, R. and Lutz, E. (2008) arXiv: 0803.4067v1.
- 16. Purwanto, A., Sukamto, H. and Subagyo, B.A. (2015) Quantum Carnot Heat Engine Efficiency with Minimal Length. Journal of Modern Physics, 6, 2297-2302.
http://dx.doi.org/10.4236/jmp.2015.615234 - 17. Munoz, E. and Pena, F.J. (2012) Quantum Heat Engine in the Relativistic Limit: The Case of a Dirac Particle. Physical Review E, 86, Article ID: 061108.
http://dx.doi.org/10.1103/PhysRevE.86.061108 - 18. Ferre, M., Orellana, P.A., Pena, F.J., Rojas, R.G. and Vargas, P. (2016) arXiv: 1603.04084v1.






