Received 1 April 2016; accepted 21 May 2016; published 24 May 2016

ABSTRACT

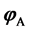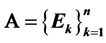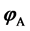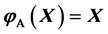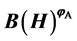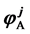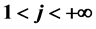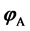Let be a normal completely positive map with Kraus operators. An operator X is said to be a fixed point of, if. Let be the fixed points set of. In this paper, fixed points of are considered for, where means j-power of. We obtain that 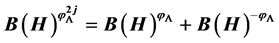and 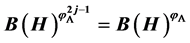for integral 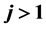when A is self-adjoint and commutable. Moreover, 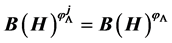holds under certain condition.

Keywords:

Fixed Point, Power, Completely Positive Map

1. Introduction

Completely positive maps are founded to be very important in operator algebras and quantum information. Especially recent years, it has a great development since a quantum channel can be represented by a trace preserving completely positive map. Fixed points of completely positive map are useful in theory of quantum error correction and quantum measurement theory and have been studied in several papers from different aspects, many interesting results have been obtained (see [1] - [12] ).

For the convenience of description, let H be a separable complex Hilbert space and 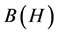be the set of all bounded linear operators on H. Let on be a contractive map. As we know, every contractive and normal (or weak continuous) completely positive map on is determined by a row contraction on H in the sense that

where if, the convergence is in the weak * topology (see [13] and [14] ) and then denoting, we call a completely positive map associated with A.

Let be an at most countable subset of with, where the series is convergent in the strong operator topology. In this case, A is called a row contraction. Then is well defined on and also a normal completely positive map. Moreover, we denote j-power for by, that is. In addition, For a row contraction, we say that the operator sequence A is unital if is commutative, if for all is normal, if each is normal and positive, and if every is positive. If A is unital (resp. commutative) then we say that is unital (resp. commutative). Moreover, or A is called trace preserving if. For a subset, we denote the commutant of S in by. We say that an is a fixed point of or a fixed point associated to the row contraction A if. Let be the set of fixed points of. Some authors compared the commutant of, where, and some conditions for which are given (as in [1] , [10] ).

For a trace preserving quantum operation, it was proved that if

in [1] . And, if Kraus operators A is a spherical unitary [10] . On the other hand, the authors [12] consider some conditions for a unital and commuting row contraction A to be normal and therefore in those cases. Moreover, the fixed points set of is represented when A is a commuting and trace preserving row contraction [15] .

The purpose of this paper is to investigate fixed points of j-power of the completely positive map for

. It is obtained that and when A is self-adjoint and commutable. Furthermore, holds under certain condition.

2. Main Results

In this section, let A be a normal and commuting row contraction. To give main results, we begin with some notations and lemmas. Let be the strong operator topology limit of.

Lemma 1 ( [10] ) Let be a unital and normal commuting row contractions. Then.

Lemma 2 ( [10] ) Let be a commuting row contraction. If, then there exists a triple where K is a Hilbert space, is a bounded operator from K to H and is a spherical unitary on K satisfying the following properties:

1);

2) for all k;

3) K is the smallest reducing subspace for containing;

4) The mapping

defined by

is a complete isometry from the commutant of onto the space;

5) There exists a *-homomorphism such that

.

Lemma 3 ( [16] ) (Fuglede-Putnam Theorem) Let, if A and B are normal, then implies.

In general, there is no concrete relation between and for different positive integers k and j.

Example 4 Let and, then is well defined and . However, by a direct computation, and. Hence,.

But if A is self-adjoint and commutable, the following result holds.

Theorem 5 If A is unital, self-adjoint and commutable, then and for any.

Proof. For any, we first prove. For any, then. So for any j. It is only to prove. According to A is unital, self- adjoint and commutable, then is so. For any operator, then A and are commutable for any k by lemma 1. By the function calculus, A and are commutable

since is self-adjoint, and so. Therefore,

.

Next, we prove. For any, then

, for any.

So since, thus. It follows that

and. So. Conversely, for any,, then. So for any j. Therefore. So and . Therefore, the result holds. This completes the proof.

Corollary 6 Let be unital, self-adjoint and commutable, then

,

where

Proof. From Theorem 5 and Lemma 1, it is only to prove that. Let and, for any operator, then.

From Lemma 1, we have

.

It follows that for any k and then. This completes the proof.

Theorem 7 Let be unital and commutable. Supposing that there is an such that is positive and invertible, then, where.

Proof. From Lemma 2, there exists a triple where K is a Hilbert space, is abounded operator and is a normal unital and commuting operator sequence on K having the properties 1); 2); 3) K is the smallest reducing subspace for containing; 4) The mapping defined by and is a complete isometry from the commutant of onto the space; also it is obtained that for any k, where is a unital *-homomorphism. Then is positive and invertible since is positive and invertible. Next, we write and for any. In fact, if and only if for any. On one hand, if; on the other hand, if, then and so by the function calculus. Moreover, , thus since is invertible. That is to say, and have the same reducing subspace. It follows that K is also the smallest reducing subspace for the unital, normal and commuting operator sequence containing. Thus is also a complete isometry from the commutant of onto the space. Combining with, it is easy to get. The proof is completed.

Acknowledgements

This research was supported by the Natural Science Basic Research Plan of Henan Province (No. 14 B110010 and No. 1523000410221).

Cite this paper

Haiyan Zhang,Hongying Si, (2016) Fixed Points Associated to Power of Normal Completely Positive Maps*. Journal of Applied Mathematics and Physics,04,925-929. doi: 10.4236/jamp.2016.45101

References

NOTES

^*Fixed points of completely positive maps.