Journal of Applied Mathematics and Physics
Vol.04 No.03(2016), Article ID:65208,7 pages
10.4236/jamp.2016.43062
On Two Extension Formulas for Lauricella’s Function of the Second Kind of Several Variables
Ahmed Ali Atash1, Ahmed Ali Al-Gonah2
1Department of Mathematics, Faculty of Education-Shabwah, Aden University, Aden, Yemen
2Department of Mathematics, Faculty of Education-Aden, Aden University, Aden, Yemen

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 February 2016; accepted 27 March 2016; published 30 March 2016
ABSTRACT
The aim of this research paper is to derive two extension formulas for Lauricella’s function of the second kind of several variables with the help of generalized Dixon’s theorem on the sum of the series 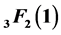 obtained by Lavoie et al. [1] . Some special cases of these formulas are also deduced.
obtained by Lavoie et al. [1] . Some special cases of these formulas are also deduced.
Keywords:
Extension Formulas, Lauricella’s Function, Dixon’s Theorem, Hypergeometric Functions

1. Introduction
The Lauricella’s function 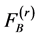 is defined and represented as follows [2]
is defined and represented as follows [2]
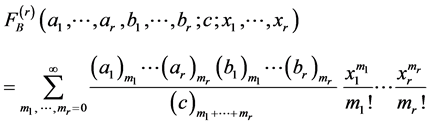 (1.1)
(1.1)
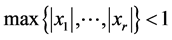 ;
;
where 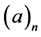 denotes the Pochhammer’s symbol defined by
denotes the Pochhammer’s symbol defined by
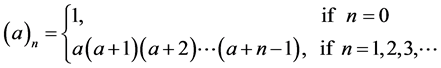 (1.2)
(1.2)
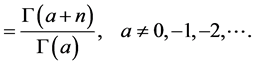 (1.3)
(1.3)
Also, we note that
 (1.4)
(1.4)
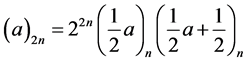 (1.5)
(1.5)
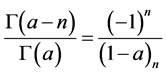 (1.6)
(1.6)
 (1.7)
(1.7)
The generalized Lauricella’s function of several variables is defined as follows [2]
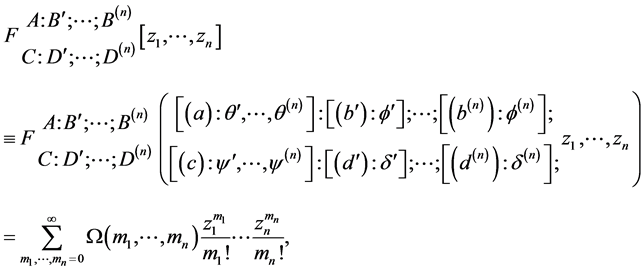 (1.8)
(1.8)
where
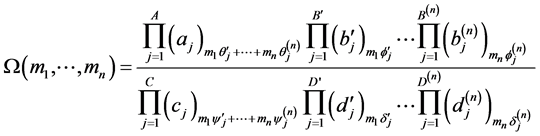 (1.9)
(1.9)
the coefficients 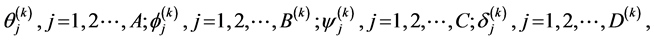 for all
for all
 are real and positive;
are real and positive; 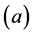
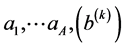
the array of 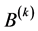
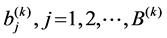
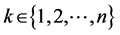
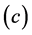
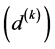
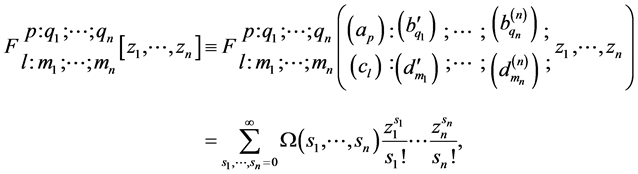
where
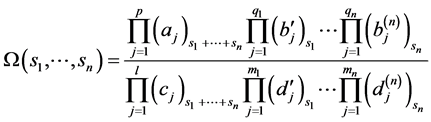
In the theory of hypergeometric series, classical summation theorems such as Dixon, Watson and Whipple for the series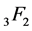
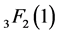
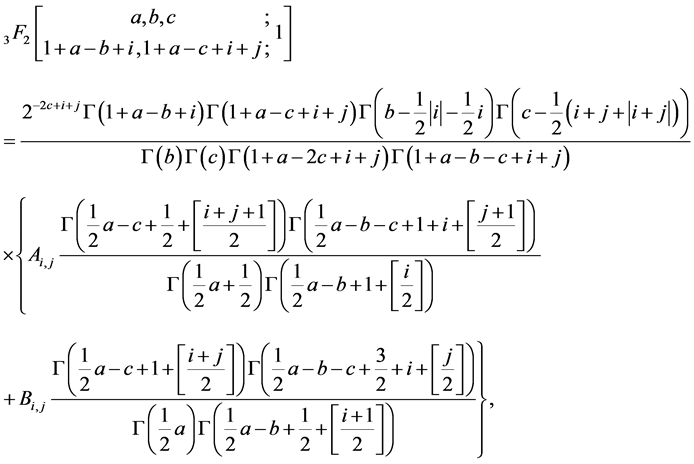
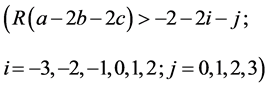
where 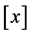
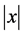
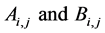
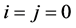
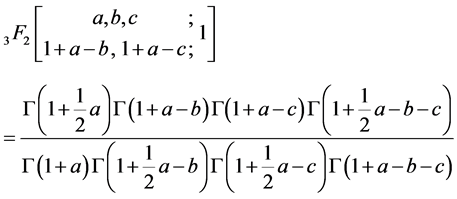
2. Extension Formulas
In this section, the following two extension formulas for Lauricella’s function of the second kind of several variables will be established:

and

where
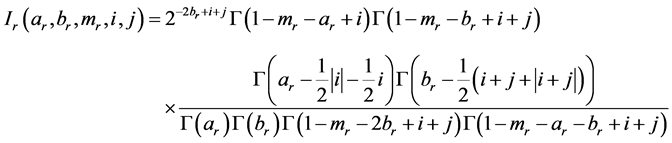
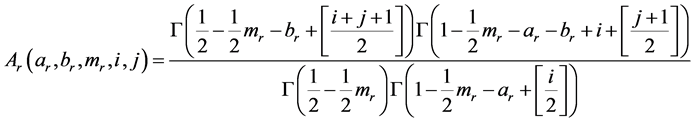
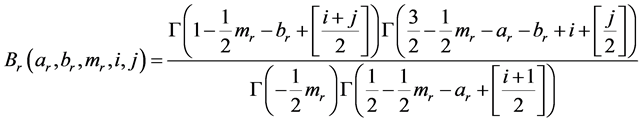
for
The coefficients 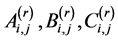
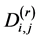
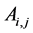
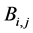
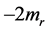
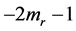
Proof of (2.1): Denoting the left hand side of (2.1) by S, expanding 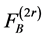
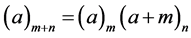
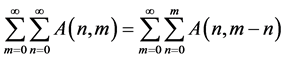
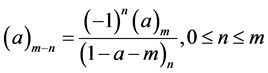
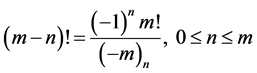
we get
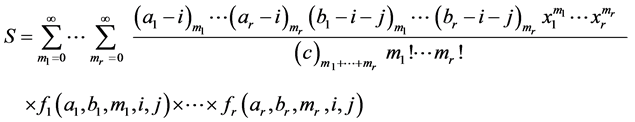
where
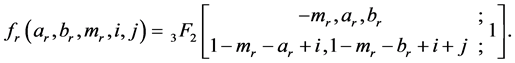
Separating (2.9) into its even and odd terms, we have

Finally, in (2.11) if we use the result (1.12), then we obtain the right hand side of (2.1). This completes the proof of (2.1). The result (2.2) can be proved by the similar manner.
3. Special Cases
1) In (2.1), if we take 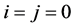
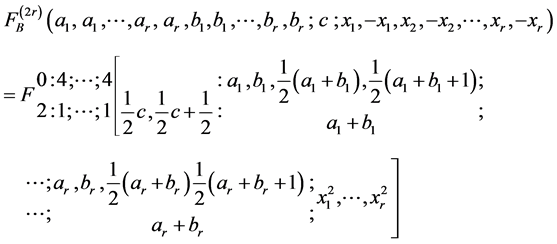
which for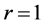
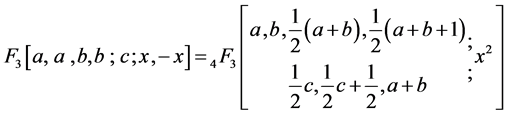
where 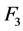
2) Similarly, in (2.2) if we take 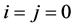
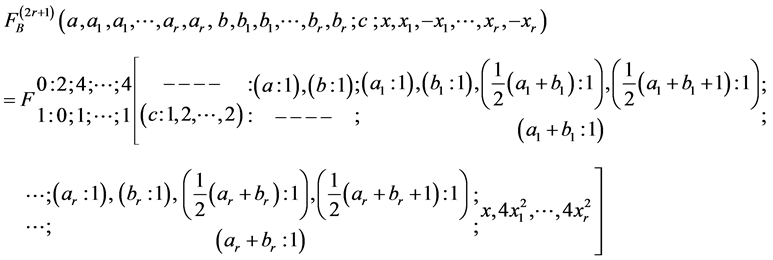
3) In (2.2) if we take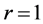
riables 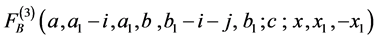
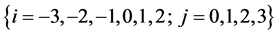
Cite this paper
Ahmed Ali Atash,Ahmed Ali Al-Gonah, (2016) On Two Extension Formulas for Lauricella’s Function of the Second Kind of Several Variables. Journal of Applied Mathematics and Physics,04,571-577. doi: 10.4236/jamp.2016.43062
References
- 1. Lavoie, J.L., Grondin, F., Rathie, A.K. and Arora, K. (1994) Generalizations of Dixon’s Theorem on the Sum of a . Mathematics of Computation, 62, 267-276.
- 2. Srivastava, H.M. and Manocha, H.L. (1984) A Treatise on Generating Functions. Hasted Press, New York.
- 3. Bailey, W.N. (1935) Generalized Hypergeometric Series. Cambridge University Press, Cambridge.
- 4. Lavoie, J.L., Grondin, F. and Rathie, A.K. (1992) Generalizations of Watson’s Theorem on the Sum of a . Indian Journal of Mathematics, 34, 23-32.
- 5. Lavoie, J.L., Grondin, F. and Rathie, A.K. (1996) Generalizations of Whipple’s Theorem on the Sum of a . Journal of Computational and Applied Mathematics, 72, 293-300.
http://dx.doi.org/10.1016/0377-0427(95)00279-0 - 6. Rainville, E.D. (1960) Special Functions. The Macmillan Company, New York.
- 7. Bailey, W.N. (1953) On the Sum of Terminating . Quarterly Journal of Mathematics Oxford, 2, 237-240.
http://dx.doi.org/10.1093/qmath/4.1.237 - 8. Atash, A.A. (2015) An Extension Formulas of Lauricella’s Functions by Applications of Dixon’s Summation Theorem. Applications and Applied Mathematics, 10, 1007-1018.