Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63794,13 pages
10.4236/jamp.2016.42037
Unsteady Heat Transfer of Viscous Incompressible Boundary Layer Fluid Flow through a Porous Plate with Induced Magnetic Field
Ariful Islam1, Muhammad Minarul Islam2, Mahabur Rahman1, Lasker Ershad Ali1, Md. Shakhaoath Khan3
1Mathematics Discipline, Khulna University, Khulna, Bangladesh
2Bangabandhu Sheikh Mujibur Rahman Science & Technology University, Gopalgonj, Bangladesh
3Discipline of Chemical Engineering, University of Newcastle, Callaghan, Australia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 January 2016; accepted 22 February 2016; published 25 February 2016
ABSTRACT
Because of the great importance of thermal instability in nature, in chemical processes, in separation processes, in industrial applications as well as in geophysical and astrophysical engineering, the effect of thermal diffusion on the combined MHD heat transfer in an unsteady flow past a continuously moving semi-infinite vertical porous plate which is subjected to constant heat has been investigated numerically under the action of strong applied magnetic field taking into account the induced magnetic field. This study is performed for cooling problem with lighter and heavier particles. Numerical solutions for the velocity field, induced magnetic field as well as temperature distribution are obtained for associated parameters using the explicit finite difference method. The obtained results are also discussed with the help of graphs to observe effects of various parameters on the above mentioned quantities.
Keywords:
Heat Transfer, Porous Medium, Induced Magnetic Field, Finite Difference Method

1. Introduction
Magnetohydrodynamics (MHD) is currently undergoing a period of great enlargement and differentiation of subject matter. The science of magnetohydrodynamics was concerned with geophysical and astrophysical problems for a number of years. In recent years, the possible use of MHD is to affect a flow stream of an electrically conducting fluid for the purpose of thermal protection, braking, propulsion and control. From the point of applications, several investigators have made model studies on the effect of magnetic field on free convection flows. Some of them are Georgantopoulos [1] , Nanousis et al. [2] and Raptis and Singh [3] . Along with the effects of magnetic field, the effect of transpiration parameter, being an effective method of controlling the boundary layer has been considered by Kafoussias [4] and Singh [5] . Singh et al. [6] studied magnetohydrodynamics heat and mass transfer flow of a viscous incompressible fluid past an infinite vertical porous plate under oscillatory suction velocity normal to the plate. The combined boundary layer heat and mass transfer of an electrically conducting fluid in MHD natural convection adjacent to a vertical surface was analyzed by Chen [7] . The boundary layer behavior and mathematical configuration was previously discussed by Sakidas [8] [9] .
All the above works are related to the stationary vertical surface. However, the flow past a continuously moving surface has many applications in manufacturing processes such as hot rolling, metal and plastic extrusion, continuous casting, and glass fiber and paper production. The heat transfer flow past a continuous moving plate with variable temperature was investigated by Soundalgekar and RamanaMurty [10] . Al-Sanea [11] studied the steady laminar flow and heat transfer characteristics of a continuously moving vertical sheet of extruded material. An analytical study of the one dimensional steady combined heat and mass transfer by mixed convection flow of an incompressible electrically conducting viscous fluid past an electrically non-conducting continuously moving infinite vertical porous plate under the action of strong magnetic field with constant suction velocity, constant heat and mass fluxes was done by Chaudhary and Sharma [12] . The level of concentration of foreign mass was assumed very low in this study so that the thermal and mass diffusion were neglected. They used perturbation technique to obtain the solution and did not show the complete results due to some analytical restrictions. Along with these studies, the effect of thermal diffusion on MHD free convection and mass transfer flows have also been considered by many investigators due to its important role particularly in isotope separation and in mixtures between gases with very light molecular weight (H2,He,) and medium molecular weight (N2, air) (Eckert and Drake, [13] ). Considering these aspects, model studies were carried out by many investigators of who the names of Kafoussias [14] , Nanousis [15] , Sattar and Alam [16] and Alam et al. [17] are worth mentioning. Recently both Soret and Dufour effects on steady mixed convection flow past a semi-infinite vertical porous flat plate in a porous medium with variable suction was investigated by Alam and Rahman [18] . Quite recently Alam et al. [19] studied Numerical Study of the Combined Free-Forced Convection and Mass Transfer Flow Past a Vertical Porous Medium with Heat Generation and Thermal Diffusion. Very recently, a number of studies of unsteady heat transfer boundary layer flow were reported in the literature [20] - [26] . However, the effect of induced magnetic is still not getting abundant attraction to the researchers.
We investigated numerically the transient heat transfer of viscous incompressible boundary layer fluid flow through a porous plate with induced magnetic field taking into account the strong magnetic field with constant heat fluxes. In this study, the viscous dissipation and joule heating terms in the energy equation have been considered for high speed flows. The governing equations of the problem contain a system of partial differential equations which are transformed by usual transformation into a non-dimensional system of partial coupled non-linear differential equations. The obtained non-similar partial differential equations solved numerically by finite difference method [27] . The results of this study will be discussed for the different values of the well- known parameters and shown graphically.
2. Mathematical Formulations
From the basis of studying Magneto Fluid Dynamics (MFD), for a boundary layer [8] [9] heat transfer by mixed convection flow of an electrically conducting viscous fluid that approximately grossly neutral with induced magnetic field, thermal diffusion, constant heat and mass fluxes, the generalized continuity equation, momentum equation, magnetic induction equation, energy equation and species equation together with the Ohm’s law and Maxwell’s equations are as furnished below,
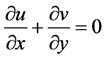 (1)
(1)
 (2)
(2)
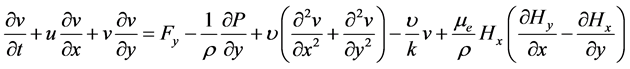 (3)
(3)
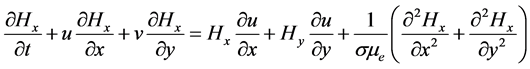 (4)
(4)
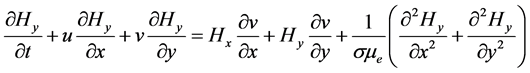 (5)
(5)
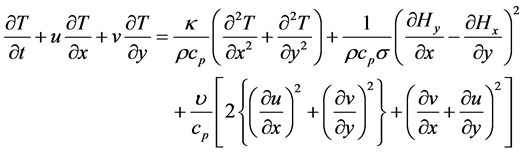 (6)
(6)
Initially we consider that the plate as well as the fluid is at the same temperature 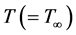 everywhere in the fluid is same. Also it is assumed that the fluid and the plate is at rest initially in its own plane and instantaneously at time
everywhere in the fluid is same. Also it is assumed that the fluid and the plate is at rest initially in its own plane and instantaneously at time , the temperature of the plate is raised to
, the temperature of the plate is raised to 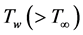 , which is there after maintained constant, where
, which is there after maintained constant, where  is the temperature at the wall and
is the temperature at the wall and  is the temperature of the species far away from the plate.
is the temperature of the species far away from the plate.
The x-component of the momentum equation reduces to the boundary layer equation if the only contribution to the body force is made by gravity, the body force per unit volume, 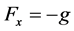 , where g is the local acceleration due to gravity. The physical model of this study is provided in Figure 1.
, where g is the local acceleration due to gravity. The physical model of this study is provided in Figure 1.
There is no body force in the y-direction i.e. 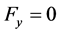 thus
thus 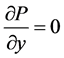 which implies that
which implies that . Hence the x-component pressure gradient at any point in the boundary layer must equal to the pressure gradient in the quiescent region outside the boundary layer. However, in this region,
. Hence the x-component pressure gradient at any point in the boundary layer must equal to the pressure gradient in the quiescent region outside the boundary layer. However, in this region,




With the help of the Equation (7), the momentum Equations (2) and (3) become
Figure 1. Physical configuration and coordinate system.


The magnetic Reynolds number of the flow is not taken to the small enough so that the induced magnetic field 










By neglecting the small order terms from the Equations (10) to (15) we get
Continuity equation

Momentum equation

Magnetic induction equation

Energy equation

and the corresponding initial and boundary conditions for the problem are everywhere





where x, y are Cartesian coordinate system; u, v are x, y component of flow velocity respectively; g is the local acceleration due to gravity; 









Since the solutions of the governing Equations (16) to (19) under the initial (20) and boundary (21) conditions will be based on the finite difference method it is required to make the said equations dimensionless [27] . After introducing the dimensionless quantities and proper simplifications we obtain the following nonlinear coupled partial differential equations in terms of dimensionless variables,




Also the associated initial (20) and boundary (21) conditions becomes





3. Important Physical Parameters






4. Numerical Solutions
Now we attempt to solve the governing second order nonlinear coupled dimensionless partial differential equations with the associated initial and boundary conditions. For solving a transient free convection flow with mass transfer past a semi-infinite plate, Carnahan et al. [25] used the explicit finite difference method which is conditionally stable. On the contrary, the same problem was studied by Soundalgekar and Ramana Murty [10] by an implicit finite difference method which is unconditionally stable. The only difference between the two methods is that the implicit method being unconditionally stable is less expansive from the point of view of computer time. However, these two methods respectively employed by Carnahan et al. [27] and Soundalgekar and RamanaMurty [10] produced the same results.
From the concept of the above discussion, for simplicity the explicit finite difference method has been used to solve Equations (22) to (25) subject to the conditions given by (26) and (27). To obtain the difference equations the region of the flow is divided into a grid or mesh of lines parallel to X and Y axes where X-axis is taken along the plate and Y-axis is normal to the plate.
Let









Also the related boundary conditions are




Here the subscripts i and j designate the grid points with x and y coordinates respectively and the superscript n represents a value of time, 






tions (29) to (31) are treated as constants. Then at the end of any time-step



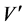


5. Results and Discussion
For the purpose of discussing the results of the problem, the approximate solutions are obtained for various parameters with small values of Eckert number. In order to analyze the physical situation of the model, we have
computed the steady state numerical values of the non-dimensional velocity U, induced magnetic field 





Figure 2. Velocity profiles for different values of 





Figure 3. Velocity profiles for different values of 





Figure 4. Velocity profiles for different values of 





Figure 5. Velocity profiles for different values of 





Figure 6. Induced magnetic fields for different values of 





Figure 7. Induced magnetic fields for different values of 





Figure 8. Induced magnetic fields for different values of 





Figure 9. Induced magnetic fields for different values of 





Figure 10. Temperature profiles for different values of 





Figure 11. Temperature profiles for different values of 


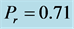


Figure 12. Temperature profiles for different values of 





Figure 13. Temperature profiles for different values of 





To get the steady state solutions, the computations have been carried out up to


Because of the special importance of cooling problem in nuclear engineering in connection with the cooling of reactors, the value of the Grashof number for heat transfer is taken to be positive 



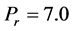





Along with the obtained steady state solutions, the flow behaviors in case of cooling problem are discussed graphically. The profiles of the transient velocity, induced magnetic field and temperature versus Y are illustrated in Figures 2-13.
The velocity profiles are shown on Figures 2-5. From these Figures, we see that, as the values of Grashof number (
From the Figures 6-9 it is observed that the induced magnetic field decreases as the value of the Grashof number (
Finally the influence of Grashof number (



6. Conclusions
An unsteady heat transfer flow through an electrically conducting incompressible viscous fluid past an electrically non-conducting continuously moving semi-infinite vertical plate under the action of strong magnetic field taking into account the induced magnetic field constant heat is investigated in this work. The resulting governing system of dimensionless coupled non-linear partial differential equations is numerically solved by an explicit finite difference method. The results are discussed for different values of important parameters as Magnetic Force Number, Magnetic diffusivity numbers, Grashof number, Prandtl number and Eckert number. Some of the important findings obtained from the graphical representation of the results are listed herewith;
The velocity & temperature profiles increases, when the value of 
The magnetic induction decreases with the increases of
As the basis for many scientific and engineering applications for studying more complex vertical problems involving the flow of electrically conducting fluids, it is hoped that the present investigation of the study of applied physics of flow over a vertical surface can be utilized. In the migration of underground water or oil as well as in the filtration and water purification processes, the findings may be useful for study of movement of oil or gas and water through the reservoir of an oil or gas field. The results of the problem are also of great interest in geophysics and astrophysics in the study of interaction of the geomagnetic field with the fluid in geothermal region.
Acknowledgements
We are extremely thankful to Khulna University for giving a lot of support during this research work at the Mathematics Laboratory, Mathematics Discipline, Science Engineering & Technology School, Khulna University, Khulna, Bangladesh.
Cite this paper
ArifulIslam,Muhammad MinarulIslam,MahaburRahman,Lasker ErshadAli,Md. ShakhaoathKhan, (2016) Unsteady Heat Transfer of Viscous Incompressible Boundary Layer Fluid Flow through a Porous Plate with Induced Magnetic Field. Journal of Applied Mathematics and Physics,04,294-306. doi: 10.4236/jamp.2016.42037
References
- 1. Georgantopoulos, G.A. (1979) Effects of Free Convection on the Hydromagnetic Accelerated Flow past a Vertical Porous Limiting Surface. Astrophysics and Space Science, 65, 433-441.
http://dx.doi.org/10.1007/BF00648508 - 2. Nanousis, N., Georgantopoulos, G.A. and Papaioannou, A. (1980) Hydromagnetic Free Convection Flow in the Stokes Problem for a Porous Vertical Limiting Surface with Constant Suction. Astrophysics and Space Science, 70, 377-383.
http://dx.doi.org/10.1007/BF00639561 - 3. Raptis, A. and Singh, A.K. (1983) MHD Free Convection Flow past an Accelerated Vertical Plate. International Communications in Heat and Mass Transfer, 10, 313-321.
http://dx.doi.org/10.1016/0735-1933(83)90016-7 - 4. Kafoussias, N.G., Nanousis, N. and Georgantopoulos, G.A. (1979) Free Convection Effects on the Stokes Problem for an Infinite Vertical Limiting Surface with Constant Suction. Astrophysics and Space Science, 64, 391-399.
http://dx.doi.org/10.1007/BF00639516 - 5. Singh, A.K. (1982) MHD Free Convection Flow in the Stokes Problem for a Porous Vertical Plate. Astrophysics and Space Science, 87, 455-461.
http://dx.doi.org/10.1007/BF00648936 - 6. Singh, A.K., Singh, Aj.K. and Singh, N.P. (2003) Heat and Mass Transfer in a MHD Flow of a Viscous Fluid past Vertical Plate under Oscillatory Suction Velocity. Indian Journal of Pure and Applied Mathematics, 34, 429-442.
- 7. Chen, C.H. (2004) Combined Heat and Mass Transfer in MHD Free Convection from a Vertical Surface with Ohmic Heating and Viscous Dissipation. International Journal of Engineering Science, 42, 699-713.
http://dx.doi.org/10.1016/j.ijengsci.2003.09.002 - 8. Sakiadis, B.C. (1961) Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for Two-Dimensional and Axisymmetric Flow. American Institute of Chemical Engineer, 7, 26-28.
http://dx.doi.org/10.1002/aic.690070108 - 9. Sakiadis, B.C. (1961) Boundary-Layer Behavior on Continuous Solid Surfaces: II. The Boundary Layer on a Continuous at Surface. American Institute of Chemical Engineer, 7, 221-225.
http://dx.doi.org/10.1002/aic.690070211 - 10. Soundalgekar, V.M. and RamanaMurty, T.V. (1980) Heat Transfer Flow past a Continuous Moving Plate with Variable Temperature. Warme-Und Stoffubertrag, 14, 91-93.
http://dx.doi.org/10.1007/BF01806474 - 11. Al-Sanea, S.A. (2004) Mixed Convection Heat Transfer along a Continuously Moving Heated Vertical Plate with Suction or Injection. International Journal of Heat and Mass Transfer, 47, 1445-1465.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2003.09.016 - 12. Chaudhary, R.C. and Sharma, B.K. (2006) Combined Heat and Mass Transfer by Laminar Mixed Convection Flow from a Vertical Surface with Induced Magnetic Field. Journal of Applied Physics, 99, Article ID: 034901.
http://dx.doi.org/10.1063/1.2161817 - 13. Eckert, E.R.G. and Drake, R.M. (1972) Analysis of Heat and Mass Transfer. McGraw-Hill Book Co., New York.
- 14. Kafoussias, N.G. (1992) MHD Thermal-Diffusion Effects on Free-Convective and Mass-Transfer Flow over an Infinite Vertical Moving Plate. Astrophysics and Space Science, 192, 11-19.
http://dx.doi.org/10.1007/BF00653255 - 15. Nanousis, N. (1992) Thermal-Diffusion Effects on MHD Free Convective and Mass Transfer Flow past a Moving Infinite Vertical Plate in a Rotating System. Astrophysics and Space Science, 191, 313-322.
http://dx.doi.org/10.1007/BF00644779 - 16. Sattar, M.A. and Alam, M.M. (1994) Thermal-Diffusion as Well as Transpiration Effects on MHD Free Convection and Mass Transfer Flow past an Accelerated Vertical Porous Plate. Indian Journal of Pure and Applied Mathematics, 25, 679-688.
- 17. Alam, M.S., Rahman, M.M. and Samad, M.A. (2006) Dufour and Soret Effects on Unsteady MHD Free Convection and Mass Transfer Flow past a Vertical Porous Medium. Nonlinear Analysis: Modelling and Control, 11, 217-226.
- 18. Alam, M.S. and Rahman, M.M. (2006) Dufour and Soret Effects on Mixed Convection Flow past a Vertical Porous Flat Plate with Variable Suction. Nonlinear Analysis: Modelling and Control, 11, 3-12.
- 19. Alam, M.S., Rahman, M.M. and Samad, M.A. (2006) Numerical Study of the Combined Free-Forced Convection and Mass Transfer Flow past a Vertical Porous Medium with Heat Generation and Thermal Diffusion. Nonlinear Analysis: Modelling and Control, 11, 331-343.
- 20. Ferdows, M., Khan, M.S., Bég, O.A. and Alam, M.M. (2013) Numerical Study of Transient Magnetohydrodynamic Radiative Free Convection Nanofluid Flow from a Stretching Permeable Surface. Journal of Process Mechanical Engineering, 228, 181-196.
http://dx.doi.org/10.1177/0954408913493406 - 21. Khan, M.S., Karim, I., Ali, L.E. and Islam, A. (2012) MHD Free Convection Boundary Layer Unsteady Flow of a Nanofluid along a Stretching Sheet with Thermal Radiation and Viscous Dissipation Effects. International Nano Letters, 2, 1-9.
http://dx.doi.org/10.1186/2228-5326-2-24 - 22. Beg, O.A., Khan, M.S., Karim, I., Alam, M.M. and Ferdows, M. (2013) Explicit Numerical Study of Unsteady Hydromagnetic Mixed Convective Nanofluid Flow from an Exponential Stretching Sheet in Porous Media. Applied Nanoscience, 4, 943-957.
http://dx.doi.org/10.1007/s13204-013-0275-0 - 23. Khan, M.S., Wahiduzzaman, M., Karim, I., Islam, M.S. and Alam, M.M. (2014) Heat Generation Effects on Unsteady Mixed Convection Flow from a Vertical Porous Plate with Induced Magnetic Field. Procedia Engineering, 90, 238-244.
http://dx.doi.org/10.1016/j.proeng.2014.11.843 - 24. Khan, M.S., Karim, I. and Biswas, M.H.A. (2012) Heat Generation, Thermal Radiation and Chemical Reaction Effects on MHD Mixed Convection Flow over an Unsteady Stretching Permeable Surface. International Journal of Basic and Applied Science, 1, 363-377.
- 25. Islam, M., Akter, F. and Islam, A. (2015) Mass Transfer Flow through an Inclined Plate with Porous Medium. American Journal of Applied Mathematics, 3, 215-220.
http://dx.doi.org/10.11648/j.ajam.20150305.12 - 26. Ali, L.E., Islam, A. and Islam, N. (2015) Investigate Micropolar Fluid Behavior on MHD Free Convection and Mass Transfer Flow with Constant Heat and Mass Fluxes by Finite Difference Method. American Journal of Applied Mathematics, 3, 157-168.
http://dx.doi.org/10.11648/j.ajam.20150303.23 - 27. Carnahan, B., Luther, H.A. and Wilkes, J.O. (1969) Applied Numerical Methods. Wiley, New York.
Nomenclature




















