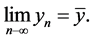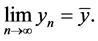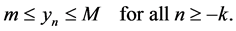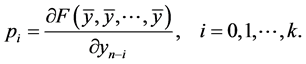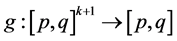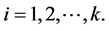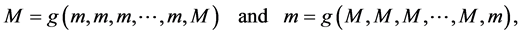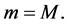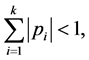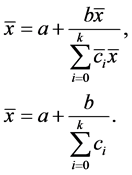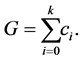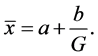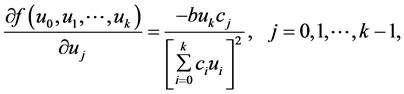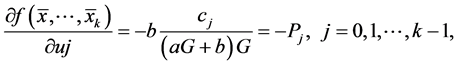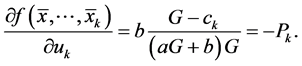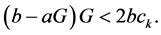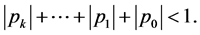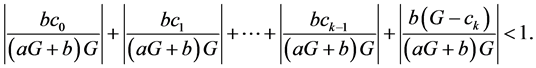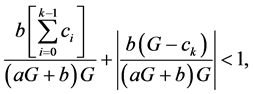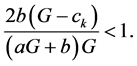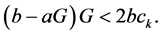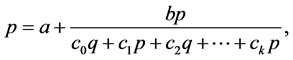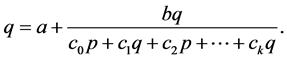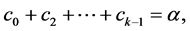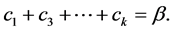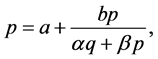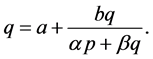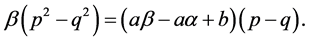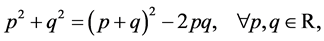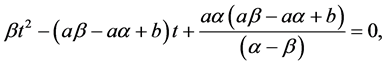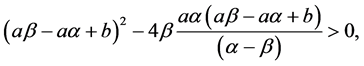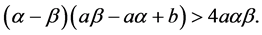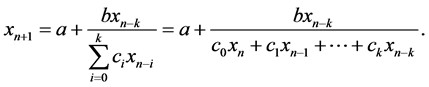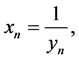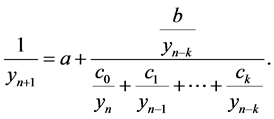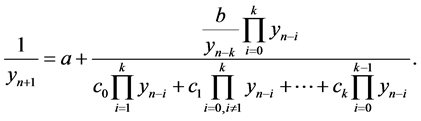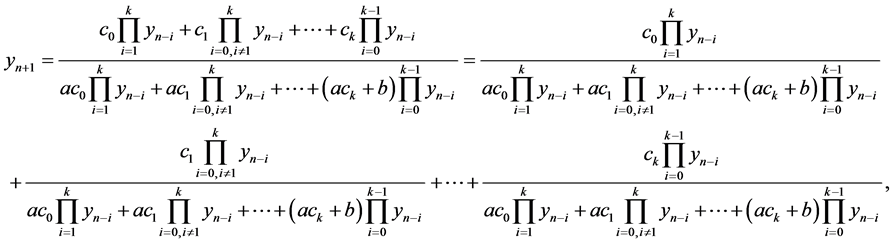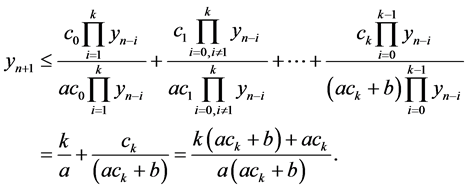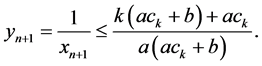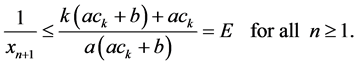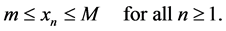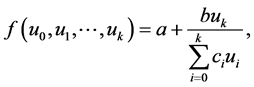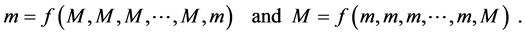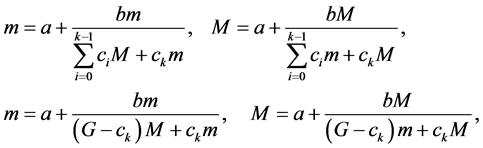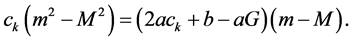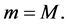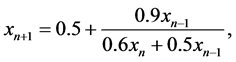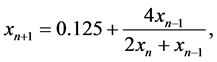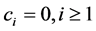Journal of Applied Mathematics and Physics
Vol.04 No.01(2016), Article ID:63049,10 pages
10.4236/jamp.2016.41014
On the Nonlinear Difference Equation
Elmetwally M. Elabbasy, Abdulmuhaemn A. El-Biaty Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 November 2015; accepted 22 January 2016; published 26 January 2016
ABSTRACT
In this paper, we investigate some qualitative behavior of the solutions of the difference equation 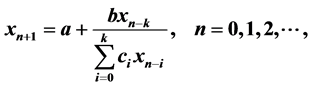 where the coefficients a, b and
where the coefficients a, b and 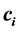 are positive real numbers,
are positive real numbers, 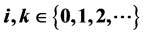 and where the initial conditions
and where the initial conditions 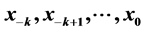 are arbitrary positive real numbers.
are arbitrary positive real numbers.
Keywords:
Difference Equation, Stability, Periodicity, Boundedness, Global Stability

1. Introduction
Our aim in this paper is to study with some properties of the solutions of the difference equation
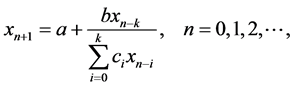 (1.1)
(1.1)
where the coefficients 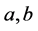 and
and 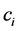 are positive real numbers,
are positive real numbers, 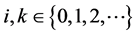 and where the initial conditions
and where the initial conditions 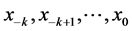 are arbitrary positive real numbers. There is a class of nonlinear difference equations, known as the rational difference equations, each of which consists of the ratio of two polynomials in the sequence terms in the same form. There has been a lot of work concerning the global asymptotics of solutions of rational difference equations [1] -[8] .
are arbitrary positive real numbers. There is a class of nonlinear difference equations, known as the rational difference equations, each of which consists of the ratio of two polynomials in the sequence terms in the same form. There has been a lot of work concerning the global asymptotics of solutions of rational difference equations [1] -[8] .
Many researchers have investigated the behavior of the solution of difference equation. For example:
Amleh et al. [9] has studied the global stability, boundedness and the periodic character of solutions of the equation
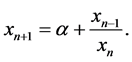
Our aim in this paper is to extend and generalize the work in [9] , [10] and [11] . That is, we will investigate the global behavior of (1.1) including the asymptotical stability of equilibrium points, the existence of bounded solution, the existence of period two solution of the recursive sequence of Equation (1).
Now we recall some well-known results, which will be useful in the investigation of (1.1) and which are given in [12] .
Let I be an interval of real numbers and let
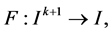
where F is a continuous function. Consider the difference equation
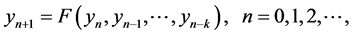 (1.2)
(1.2)
with the initial condition 
Definition 1. (Equilibrium Point)
A point 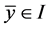 is called an equilibrium point of Equation (1.2) if
is called an equilibrium point of Equation (1.2) if
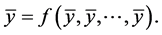
That is, 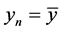
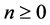
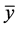
Definition 2. (Stability)
Let 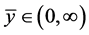
1) An equilibrium point 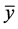
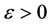
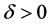
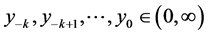
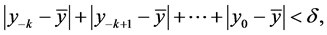
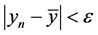
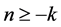
2) An equilibrium point 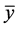
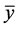
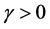
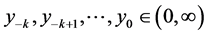
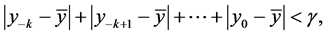
3) An equilibrium point 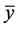
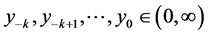
4) An equilibrium point 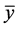
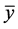
5) An equilibrium point 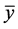
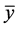
Definition 3. (Permanence)
Equation (1.2) is called permanent if there exists numbers m and M with 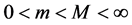
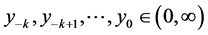
Definition 4. (Periodicity)
A sequence 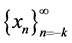
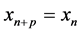
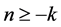
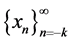
The linearized equation of Equation (1.2) about the equilibrium point 
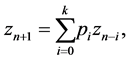
where
The characteristic equation associated with Equation (1.3) is
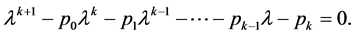
Theorem 1.1. [13] Let 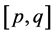
is a continuous function satisfying the following properties:
(a) 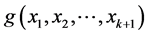
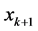
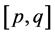
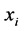
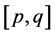
(b) If 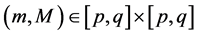
implies
Theorem 1.2. [12] Assume that F is a 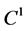
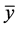
1) If all roots of Equation (1.4) lie in the open unit disk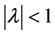
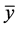
2) If at least one root of Equation (1.4) has absolute value greater than one, then the equilibrium point 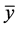
3) If all roots of Equation (1.4) have absolute value greater than one, then the equilibrium point 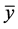
Theorem 1.3. [14] Assume that 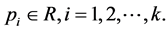
is a sufficient condition for the asymptotically stable of Equation (1.5)

2. Local Stability of Equation (1.1)
In this section we investigate the local stability character of the solutions of Equation (1.1). Equation (1.1) has a unique nonzero equilibrium point
Let
Then, we get
Let 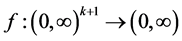
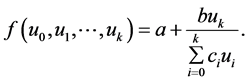
Therefore it follows that
and
Then we see that
and
Then the linearized equation of (1.1) about 
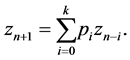
Theorem 2.1. Assume that
Then the equilibrium point of Equation (1.1) is locally stable.
Proof. It is follows by Theorem (1.3) that, Equation (2.2) is locally stable if
That is
This implies that
then
Thus
Hence, the proof is completed.
3. Periodic Solutions
In this section we investigate the periodic character of the positive solutions of Equation (1.1).
Theorem 3.1. Equation (1.1) has positive prime period-two solution only if
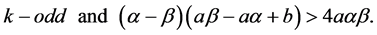
Proof. Assume that there exists a prime period-two solution
of (1.1). Let 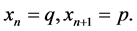
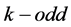
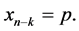
and
Let
and
Then
and
Then
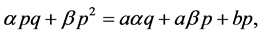
and
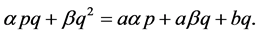
Subtracting (3.2) from (3.3) gives
Since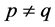
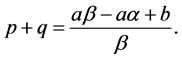
Also, since p and q are positive, 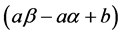
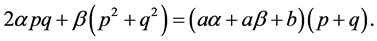
It follows by (3.4), (3.5) and the relation
that
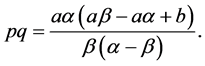
Assume that p and q are two distinct real roots of the quadratic equation
and so
which is equivalent to
Thus, the proof is completed.
4. Bounded Solution
Our aim in this section we investigate the boundedness of the positive solutions of Equation (1.1).
Theorem 4.1. The solutions 
Proof. Let 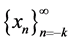
Then
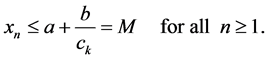
On the other hand, we see that the change of variables
transforms Equation (1.1) to the following form:
Hence, we obtain
Thus
and so,
It follows that
Thus we obtain
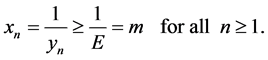
From (4.1) and (4.2) we see that
Therefore every solution of Equation (1.1) is bounded.
5. Global Stability of Equation (1.1)
Our aim in this section we investigate the global asymptotic stability of Equation (1.1).
Theorem 5.1. If 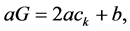
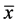
Proof. Let 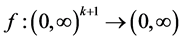
then we can see that the function 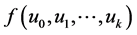
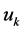
Suppose that 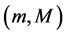
Then from Equation (2.1), we see that
then
Thus
It follows by Theorem (1.1) that 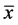
6. Numerical
For confirming the results of this section, we consider numerical examples which represent different types of solution of Equation (1.1).Example
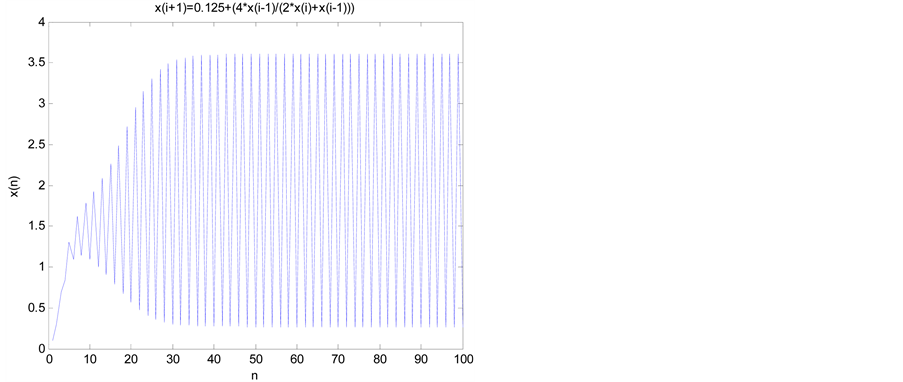
Examples 6.1. Consider the difference equation
where 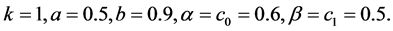
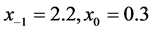
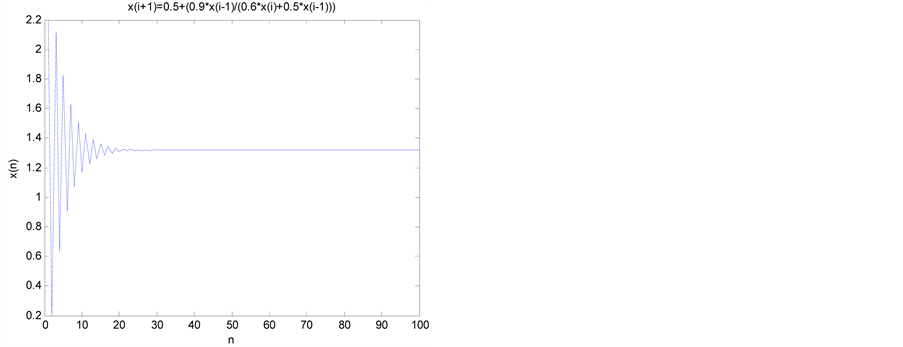
Example 6.2. Consider the difference equation
where 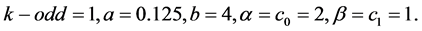
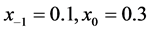
Figure 1. Ref. b1.
Table 1. The equilibrium point of Equation (1.1).
Figure 2. Ref. b4.
Table 2. The initial data satisfies condition (3.1) of Theorem (3.1).
Remark 6.1. Note that the special cases of Equation (1.1) have been studied in [9] when 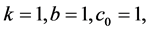
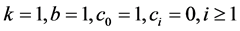
Cite this paper
Elmetwally M.Elabbasy,Abdulmuhaemn A.El-Biaty, (2016) On the Nonlinear Difference Equation. Journal of Applied Mathematics and Physics,04,100-109. doi: 10.4236/jamp.2016.41014
References
- 1. Elabbasy, E.M., El-Metwally, H. and Elsayed, E.M. (2005) On the Periodic Nature of Some Max-Type Difference Equations. International Journal of Mathematics and Mathematical Sciences, 2005, 2227-2239.
http://dx.doi.org/10.1155/IJMMS.2005.2227 - 2. Elabbasy, E.M., El-Metwally, H. and Elsayed, E.M. (2006) On the Difference Equation . Advances in Difference Equations, 1-10(2006), Article ID: 82579.
- 3. Elabbasy, E.M., El-Metwally, H. and Elsayed, E.M. (2007) Qualitative Behavior of Higher Order Difference Equation. Soochow Journal of Mathematics, 33, 861-873.
- 4. El-Moneam, M.A. and Zayed, E. (2014) Dynamics of the Rational Difference Equation
. DCDIS Series A: Mathematical Analysis, 21, 317-331. - 5. Elaydi, S.N. (1996) An Introduction to Difference Equations, Undergraduate Texts in Mathematics. Springer, New York.
http://dx.doi.org/10.1007/978-1-4757-9168-6 - 6. Kocic, V.L. and Ladas, G. (1993) Global Behavior of Nonlinear Difference Equations of Higher Order with Applications. Kluwer Academic Publishers, Dordrecht.
- 7. Stevic, S. (2005) On the Recursive Sequence . Taiwanese Journal of Mathematics, 9, 583-593.
- 8. Zayed, E. and EI-Moneam, M.A. (2010) On the Rational Recursive Sequence . Mathematica Bohemica, 135, 319-363.
- 9. Amleh, A.M., Grove, E.A., Georgiou, D.A. and Ladas, G. (1999) On the Recursive Sequence . Journal of Mathematical Analysis and Applications, 233, 790-798.
http://dx.doi.org/10.1006/jmaa.1999.6346 - 10. Hamza, A.E. (2006) On the Recursive Sequence . Journal of Mathematical Analysis and Applications, 322, 668-674.
http://dx.doi.org/10.1016/j.jmaa.2005.09.029 - 11. Saleh, M. and Aloqeili, M. (2005) On the Rational Difference Equation . Applied Mathematics and Computation, 171, 862-869.
http://dx.doi.org/10.1016/j.amc.2005.01.094 - 12. Grove, E.A. and Ladas, G. (2005) Periodicities in Nonlinear Difference Equations. Vol. 4, Chapman and Hall/CRC, Boca Raton.
- 13. Elabbasy, E.M., El-Metwally, H. and Elsayed, E.M. (2007) On the Difference Equations . Journal of Concrete and Applicable Mathematics, 5, 101-113.
- 14. Kulenovic, M.R.S. and Ladas, G. (2001) Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures. Chapman & Hall/CRC, Florida.
http://dx.doi.org/10.1201/9781420035384