Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61353,9 pages
10.4236/jamp.2015.311170
Solving Systems of Volterra Integral Equations with Cardinal Splines
Xiaoyan Liu1, Zhi Liu2, Jin Xie3
1Department of Mathematics, University of La Verne, La Verne, USA
2
3Institute of Scientific Computing,

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 24 September 2015; accepted 20 November 2015; published 23 November 2015

ABSTRACT
This work is a continuation of the earlier article [1] . We establish new numerical methods for solving systems of Volterra integral equations with cardinal splines. The unknown functions are expressed as a linear combination of horizontal translations of certain cardinal spline functions with small compact supports. Then a simple system of equations on the coefficients is acquired for the system of integral equations. It is relatively straight forward to solve the system of unknowns and an approximation of the original solution with high accuracy is achieved. Several cardinal splines are applied in the paper to enhance the accuracy. The sufficient condition for the existence of the inverse matrix is examined and the convergence rate is investigated. We demonstrated the value of the methods using several examples.
Keywords:
Spline Functions, Integral Equations, Numerical Methods

1. Introduction
Integral equations appear in many fields, including dynamic systems, mathematical applications in economics, communication theory, optimization and optimal control systems, biology and population growth, continuum and quantum mechanics, kinetic theory of gases, electricity and magnetism, potential theory, geophysics, etc. Many differential equations with boundary-value can be reformulated as integral equations. One example given in this paper is to use a system of integral equations to solve a third order differential equation. There are also some problems that can be expressed only in terms of integral equations. Scores of papers have appeared on solving integral equations, for examples, cf [2] - [4] .
2. Cardinal Splines with Small Compact Supports
Since the paper [5] by Schoenberg published in 1946, spline functions have been studied by many scholars extensively. Spline functions have excellent features and applications are endless (for examples, cf [6] ). The spline functions on uniform partitions are simple to construct and easy to employ, and are sufficient for a variety of applications.
The starting point is frequently the zero degree polynomial B-spline, an integral iteration formula could be used to construct higher order spline functions with higher degree of smoothness, i.e. let
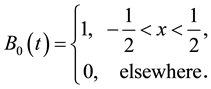
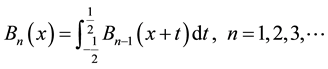 (1)
(1)
 has the global expression
has the global expression 
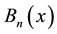 are called one dimensional B- splines, which are polynomial splines with small compact supports
are called one dimensional B- splines, which are polynomial splines with small compact supports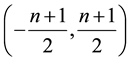 , (i.e.
, (i.e. 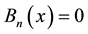 for
for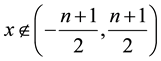 ), and excellent traits (cf [6] ). In my previous papers (cf [1] [7] - [10] ), low degree orthonormal
), and excellent traits (cf [6] ). In my previous papers (cf [1] [7] - [10] ), low degree orthonormal
spline and cardinal spline functions with small compact supports were applied in solving the second kind of linear Fredholm and Volterra integral equations.
By cardinal conditions (cf [5] ), we mean, let  be an interpolation function,
be an interpolation function, 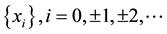 be interpolation points, then
be interpolation points, then

The lowest degree continuous cardinal spline is . To achieve higher degree of approximation, we need the cardinal spline functions with higher degree of smoothness. We employ splines that were developed in my previous papers.
. To achieve higher degree of approximation, we need the cardinal spline functions with higher degree of smoothness. We employ splines that were developed in my previous papers.
The cardinal spline  that was originally given in [11] is based on
that was originally given in [11] is based on 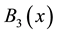 from (1) using the similar integral process. Let
from (1) using the similar integral process. Let

Then 

construction, 




To achieve higher degree of smoothness, we employ 
It is a simple calculation to check the cardinal condition is satisfied. The 



ones for


3. Numerical Methods Solving the System of Volterra Integral Equations
In this and next two sections, we are concentrating on the second kind system of linear Volterra integral equations

where
3.1. Method 1-V for Solving the System of Volterra Integral Equations
As for the Volterra system (I2), we solve it in an interval



in (I2), we get
Let

which is a simple system of 

Proposition 1. Given that







more 
where


where 
The proof is very similar to the proof of the following Proposition 3, so we skip it.
3.2. Method 2-V for Solving the Systems of Volterra Integral Equations
To achieve higher approximation rate, we plug

into (I2), where extra function values still follow the conditions (cond1) and arrive at
Let

which is still a relatively simple system of linear equations.
Remark If the integral equation (I2) has a unique solution, then the linear system (S5) is consistent. Furthermore
(where
approximates the solution of the system (I2) with a rate of
Proposition 2. Given that

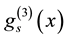




where




where 
The proof is very similar to the proof of the following Proposition 3, so we skip it.
3.3. Method 3-V for Solving the Systems of Volterra Integral Equations
To achieve higher approximation rate, we let

again we plug into (I2), where extra function values still follow the conditions (cond2) cf [9] , and we arrive at
Let

which is still a relatively simple system of linear equations.
Remark If the integral Equation (I2) has a unique solution, then the linear system (S6) is consistent. Furthermore
approximates the solution of the integral Equation (I2) with a rate of 
Proposition 3. Given that





thermore, 
where

Let 
where 
Proof. Let

where the coefficients are the solutions of above linear system (S3), and


Plug in
Therefore
4. Numerical Examples
Example 1. Consider
Let
Apply Method V-1 and solve the linear system, we obtain:
To achieve higher degree of accuracy, we apply Method V-3 and obtain :
Compare with the exact solution:
the error is 

Example 2. Given a system of linear integral equations: for
Let 



and
Since the solution is 


Example 3. Consider the third order differential equations:

with the initial condition:
Let 


Let
We apply Method V-2 and solve the linear system and arrive at the solution:
Since the exact solution is
Compare with the exact solution, the error
5. Conclusions
The system of first kind of linear Volterra integral equations has the form

where 
They can easily be transformed to the system of second kind of linear Fredholm and Volterra integral equations (cf [3] ). We can apply the similar method to solve the first and second kind Fredholm integral systems. So the proposed methods are simple and effective procedures for solving both linear system of Fredholm and Volterra integral equations.
The orthonormal and cardinal splines could also be applied to non-linear integral equations; the resulting system of coefficients will be a non-linear system, which takes more time and effort to solve. The convergence rate could be higher if we apply more complicated orthonormal or cardinal spline functions.
Acknowledgements
The work was partially funded by the National Natural Science Foundation of China under Grant no. 1471093, the Doctoral Program Foundation of the Ministry of Education of China under Grant no. 20110111120026, the Natural Science Foundation of Anhui Province of China under Grant no. 1208085MA15, the Key Project Foundation of Scientific Research, Education Department of Anhui Province under Grant no. KJ2014ZD30.
The authors thank the family members, the colleagues and administrators of the
Cite this paper
XiaoyanLiu,ZhiLiu,JinXie, (2015) Solving Systems of Volterra Integral Equations with Cardinal Splines. Journal of Applied Mathematics and Physics,03,1422-1430. doi: 10.4236/jamp.2015.311170
References
- 1. Liu, X. and Xie, J. (2014) Numerical Methods for Solving Systems of Fredholm Integral Equations with Cardinal Splines. AIP Conference Proceedings, 1637, 590.
http://dx.doi.org/10.1063/1.4904628 - 2. Adawi, A. and Awawdeh, F. (2009) A Numerical Method for Solving Linear Integral Equations. International Journal of Contemporary Mathematical Sciences, 4, 485-496.
- 3. Polyanin, A.D. (1998) Handbook of Integral Equations. CRC Press LLC, Boca Raton.
http://dx.doi.org/10.1201/9781420050066 - 4. Saeed, R.K. and Ahmed, C.S. (2008) Approximate Solution for the System of Non-Linear Volterra Integral Equations of the Second Kind by Using Block-by-block Method. Australian Journal of Basic and Applied Sciences, 2, 114-124.
- 5. Schoenberg, I.J. (1964) On Trigonometric Spline Functions. Journal of Mathematics and Mechanics, 13, 795-825.
- 6. Chui, C.K. (1988) Multivariate Splines. SIAM, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970173 - 7. Liu, X. (2001) Bivariate Cardinal Spline Functions for Digital Signal Processing. In: Kopotum, K., Lyche, T. and Neamtu, M., Eds., Trends in Approximation Theory, Vanderbilt University, Nashville, 261-271.
- 8. Liu, X. (2007) Interpolation by Cardinal Exponential Splines. The Journal of Information and Computational Science, 4, 179-194.
- 9. Liu, X. (2013) The Applications of Orthonormal and Cardinal Splines in Solving Linear Integral Equations. In: Akis, V., Ed., Essays on Mathematics and Statistics, V4, Athens Institute for Education and Research, 41-58.
- 10. Liu, X., Xie, J. and Xu, L. (2014) The Applications of Cardinal Trigonometric Splines in Solving Nonlinear Integral Equations. Applied Mathematics, 2014, Article ID: 213909.
- 11. Liu, X. (2006) Univariate and Bivariate Orthornormal Splines and Cardinal Splines on the Compact Supports. Journal of Computational and Applied Mathematics, 195, 93-105.
http://dx.doi.org/10.1016/j.cam.2005.04.070

























































