Journal of Applied Mathematics and Physics
Vol.03 No.10(2015), Article ID:60687,12 pages
10.4236/jamp.2015.310157
A Gauge Transformation between Ragnisco-Tu Hierarchy and a Related Lattice Hierarchy
Yuqing Liu1*, Chao Hu1, Juan Dai2
1School of Physics & Mathematics, Changzhou University, Changzhou, China
2Information and Technique College of Changzhou, Changzhou, China
Email: *yqmail321@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 September 2015; accepted 25 October 2015; published 28 October 2015
ABSTRACT
A new lattice hierarchy related to Ragnisco-Tu equation is proposed and its gauge equivalence to Ragnisco-Tu equation is proven. As an application of gauge transformation, we construct Darboux transformation (DT) of this new equation through DT of Ragnisco-Tu equation. An explicit exact solution is presented as an example.
Keywords:
Ragnisco-Tu Hierarchy, Gauge Transformation, Transfer Operator, Darboux Transformation

1. Introduction
Nonlinear integrable equations usually have some marvellous properties such as Hamilton structure and infinitely many conservation laws. There are close connections between many of these equations. For instance, the cerebrated KdV equation, modified KdV equation, and nonlinear Schrödinger equation are reduction of AKNS system. Boussinesq equation and derivative nonlinear Schrödinger equation are linked to the constraint of KP equation (c.f. [1] ). Jaulent-Miodek equation, Kaup-Newell equation, Levi equation and Heisenberg equation were found to be equivalent to AKNS equation [1] -[6] . The relation between two equations plays an important role, which makes one tackle with relatively unfamiliar equations through relatively familiar equations. However, in a general survey, there is comparatively less research on relatedness of lattice soliton equations than that of continuous soliton equations. One of the reasons behind this actuality is the lack of related example. In this paper we put forward a pair of nonlinear integrable lattice equations and investigate some relations such as gauge equivalence relation and Darboux transformation between them. Utilizing the relation which has been found, we will obtain an exact solution of equation.
Ragnisco-Tu equation [7] [8]
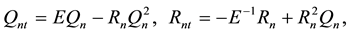 (1.1)
(1.1)
is an integrable lattice soliton equation. Ref. [8] discussed its Hamilton structure, and proved that its continuous limit may result in AKNS system. Ref. [9] obtained its inverse scattering transformation and exact solution. Ref. [10] -[12] researched more general problems, and studied Hamilton structure and Darboux transformation and geometric algerba solutions. Ragnisco-Tu equation has spectral problem [7]
 (1.2)
(1.2)
where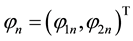 , E means a shift of space variable n, subscript t denotes partial derivative with respect to time t,
, E means a shift of space variable n, subscript t denotes partial derivative with respect to time t, 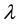 is spectral parameter and
is spectral parameter and 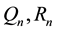 are potential functions. The derivation of equation hierarchy will be given in Section 2. This spectral problem can be generalized to
are potential functions. The derivation of equation hierarchy will be given in Section 2. This spectral problem can be generalized to
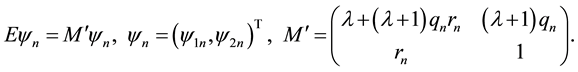 (1.3)
(1.3)
This method for constructing new lattice equation was first used in modified Toda equation [13] [14] . Surprisingly, equations obtained via these two spectral equations are equivalent, but this feature does not appear on Toda equation. On this basis, we further discuss Darboux transformation of them. With the help of gauge transformation and Darboux transformation of Ragnisco-Tu equation, we get a Darboux transformation of new equation, which is complex and difficult to construct directly.
This paper is organized as follows: in Section 2 and Section 3, we deduce the general hierarchies of Ragnisco-Tu and related generalized lattice hierarchy respectively. In Section 4, we derive a gauge transformation and transfer operator of two hierarchies. Section 5 will contribute to the Darboux transformation of two equations. Finally, in Section 6, a conclusion is presented.
2. The Derivation of Ragnisco-Tu Hierarchy
The derivation of Ragnisco-Tu hierarchy can be referred to [8] [9] , but for completeness we still give a concise version.
Consider time evolution corresponding to (1.2)
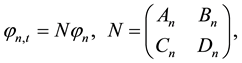 (2.1)
(2.1)
discrete zero curvature equation results in following equalities directly
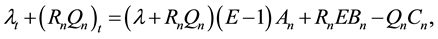 (2.2)
(2.2)
 (2.3)
(2.3)
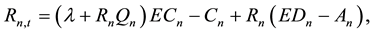 (2.4)
(2.4)
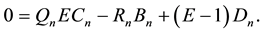 (2.5)
(2.5)
From these equations we draw out relations between related quantities
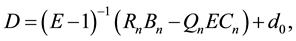 (2.6)
(2.6)
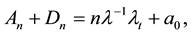 (2.7)
(2.7)
where 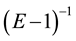 defined as
defined as 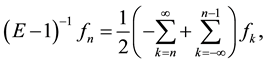 and
and 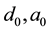 are constants independent of variable n. Let
are constants independent of variable n. Let
the relations (2.2)-(2.5) can be written as

where operators 

Giving boundary condition

and taking 

The case of k = 0 just gives Ragnisco-Tu Equation (1.1).
If the boundary condition is given as

and 

where I is an identity operator. In more general case, Ragnisco-Tu hierarchy is expressed by
Lemma 2.1. If 




then general Ragnisco-Tu hierarchy adopts the from

3. A New Lattice Hierarchy Related to the Ragnisco-Tu Hierarchy
With regard to generalized spectral problem (1.3), introduce the time evolution

Then from discrete zero curvature equation, we have




It is ease to know that there only have three independent equations, for instance, (3.2b), (3.2c), (3.2d). Now, from them we work out

and

where 


we get matrix form

Set
the general lattice hierarchy (called generalized Ragnisco-Tu hierarchy) is deduced in
Lemma 3.1. Let 





the generalized Ragnisco-Tu hierarchy is

Especially when 


The first one (k = 0) is

If we take

The first one (k = 0) is

Proof. Expanding (3.7) we have
Equating the coefficients of power of 
Through mathematical induction we get the recursion relation
From it the conclusion of Lemma 3.1 is got.
4. A Gauge Transformation and Transfer Operator between the Ragnisco-Tu Hierarchy and Generalized Ragnisco-Tu Hierarchy
In this section we will give the conclusion about gauge transformation and transfer operator between the Ragnisco-Tu hierarchy and generalized Ragnisco-Tu hierarchy.
Theorem 4.1. There exists a gauge transformation changing Lax pair of generalized Ragnisco-Tu hierarchy (1.3), (3.1) into Lax pair of Ragnisco-Tu hierarchy:

Further, potentials in (1.2) and those in (1.3) have the relations

When


where 
Proof. As gauge transformation, T should satisfy

Set

the entries of it must meet the following equations
Notice that T is independent of
Transformation matrix T also changes time evolution (3.1) into (2.1). To justify this assertion, for a newly defined 




where
It is evident that









lent to 



On the other hand, we can verify directly that

Now we deduce transfer operator of two hierarchies. A dull calculation simplifies the expression of 
Thus we have

where 

Because of in the case of iso-spectral and non-iso-spectral, the following recursion formula always holds
(In the case of iso-spectral,
(In the case of iso-spectral,

where 


According to the derivation expressions of iso-spectral and non-iso-spectral equation we arrive at the relation of two hierarchies immediately

When we focus our attention on the iso-spectral case, (4.7) holds for
which can be verified readily. When we concern about the non-iso-spectral case, (4.7) holds for

we first prove

Denote
It is ease to know “

and
Their difference is
The Equation (4.11) is proved.
On the other hand, through comparing the coefficients of 


That is

Using the recursion relations of 

Finally, we consider relevancy of two hierarchy. The time part of (4.3) has given in (4.9). The following equation is deduced according to (4.13) and (4.8)
Equation (4.11) together with above expression yields
Through mathematical induction we can prove the part of 

5. Darboux Transformation to Generalized Ragnisco-Tu Equation
Darboux transformation is a very useful tool to obtain exact solutions of nonlinear integral equation. It plays role in every type of equations such as lattice equation, discrete equation and high dimensional integral equation [15] -[22] . However, the construction of DT of complex system may still encounter difficulty. Here, we will have the aid of gauge transformation to consider DT of generalized Ragnisco-Tu equation.
5.1. Darboux Transformation to Ragnisco-Tu Equation
Consider transformation

where 

Lemma 5.1. (see also [12] ) Suppose 








where 

where 


Proof. Transformation T as DT must solve the following equation

Comparing coefficients of 




Suppose 




Transformation (5.1) also change (2.1) to time evolution which matches to
where 

We will prove that





and 





Now we deal with V11 as an example. First of all, referring to the fact that An, Dn and Bn, Cn are polynomials of 


Substituting them and (5.4) into V11 gives rise to
It is not difficult to check that 


is k + 1 power polynomial of

as 



to V12, V21, V22, the proof is similar, we do not repeat it. Now we finish the proof that (5.1) is a Darboux transformation of Ragnisco-Tu hierarchy.
As an application we present a exact solution to Ragnisco-Tu Equation (1.1). Starting from seed solution

Then according to Lemma 5.1, a solution to Ragnisco-Tu can be calculated out as follows

5.2. Darboux Transformation to Generalized Ragnisco-Tu Equation
From gauge transformation 




which forms DT of generalized Ragnisco-Tu equation. Matrix 

We can adopt simple notation to write it

where
As a DT of generalized Ragnisco-Tu equation, P should satisfy

where
From this expression, we can draw the following equalities










The acquisition of solution of them must be combined with relation exhibited in Darboux matrix (5.13). Here we do not consider general formula of solution but present a special solution related to
Notice that 

When seed solution 
These equalities produce

and

Thus we get
and form (5.17c), we obtain
Substituting it into (5.21), 

6. Conclusion
We propose a lattice equation hierarchy related to Rangnisco-Tu hierarchy (generalized RT equation) and prove that it is equivalent to Rangnisco-Tu hierarchy itself. The transfer operator of two hierarchies is obtained. As an application of gauge transformation, we obtain a Darboux transformation of generalized RT equation and acquire an exact solution of this equation.
Acknowledgements
The authors feel grateful to pertinent opinions of reviewer and careful work of editors.
Cite this paper
YuqingLiu,ChaoHu,JuanDai, (2015) A Gauge Transformation between Ragnisco-Tu Hierarchy and a Related Lattice Hierarchy. Journal of Applied Mathematics and Physics,03,1282-1294. doi: 10.4236/jamp.2015.310157
References
- 1. Chen, D.Y. (2006) Introduction of Soliton. Science Press, Beijing. (In Chinese)
- 2. Chen, D.Y. and Zeng, Y.B. (1985) The Trans-formation Operator of Nonlinear Evolution Equations I. Chinese Annals of Mathematics, 6B, 71-82.
- 3. Chen, D.Y. and Zeng, Y.B. (1985) The Transformation Operator of Nonlinear Evolution Equations III. Acta Mathematica, 28, 161-173. (In Chinese)
- 4. Chen, D.Y. and Li, Y.S. (1986) The Transformation Operator of Nonlinear Evolution Equations IV. Acta Mathematica, 29, 127-134. (In Chinese)
- 5. Chen, D.Y. and Li, Y.S. (1986) The Transformation Operator of Nonlinear Evolution Equations V. Acta Mathematica Sinica, New Series, 2, 343-356.
http://dx.doi.org/10.1007/BF02564935 - 6. Chau, L.L., Shaw, J.C. and Yen, H.C. (1992) Solving the KP Hierarchy by Gauge Transformations. Communications in Theoretical Physics, 149, 263-278.
http://dx.doi.org/10.1007/bf02097625 - 7. Zhang, H.W., Tu, G.Z., et al. (1991) Symmetries, Conserved Quantities, and Hier-archies for Some Lattice Systems with Soliton Structure. Journal of Mathematical Physics, 32, 1908-1918.
http://dx.doi.org/10.1063/1.529205 - 8. Zeng, Y.B. (1998) Restried Flows of a Hierarchy of Integrable Discrete Systems. Acta Mathematicae Applicatae Sinica, 14, 176-184.
http://dx.doi.org/10.1007/BF02677424 - 9. Liu, Y.Q. and Chen, D.Y. (2011) The Exact Solutions to a Ragnisco-Tu Hierarchy with Self-Consistent Sources. Nonlinear Analysis, 74, 5223-5237.
http://dx.doi.org/10.1016/j.na.2011.04.021 - 10. Xu, X.X. (2010) An Integrable Coupling Family of Merola-Ragnisco-Tu Lattice Systems, Its Hamiltonian Structure and Related Nonisospectral Integrable Lattice Family. Physics Letters A, 374, 401-410.
http://dx.doi.org/10.1016/j.physleta.2009.11.012 - 11. Zeng, X. and Geng, X.G. (2014) Algebro-Geometric Solutions of the Discrete Ragnisco-Tu Hierarchy. Reports on Mathematical Physics, 73, 17-48.
http://dx.doi.org/10.1016/S0034-4877(14)60030-6 - 12. Xu, X.X. (2015) Solving an Integrable Coupling System of Mer-ola-Ragnisco-Tu Lattice Equation by Darboux Transformation of Lax Pair. Communications in Nonlinear Science and Numerical Simulation, 23, 192-201.
http://dx.doi.org/10.1016/j.cnsns.2014.11.002 - 13. Xu, X.X., Yang, H.X. and Sun, Y.P. (2006) Dar-boux Transformation of the Modified Toda Lattice Equation. Modern Physics Letters B, 20, 641-648.
http://dx.doi.org/10.1142/S0217984906011025 - 14. Hon, Y.C. and Fan, E.G. (2009) Quasi-Periodic Solutions for Modified Toda Lattice Equation. Chaos, Solitons and Fractals, 40, 1297-1308.
http://dx.doi.org/10.1016/j.chaos.2007.09.008 - 15. Spiridonov, V. and Zhedanov, A. (1995) Discrete Darboux Transformations, the Discrete-Time Toda Lattice, and the Askey-Wilson Polynomials. Methods and Applications of Analysis, 2, 369-398.
- 16. Fan, E.G. (2001) Explicit N-Fold Darboux Transformations and Soliton Solutions for Nonlinear Derivative Schrödinger Equations. Com-munications in Theoretical Physics, 35, 651-656.
http://dx.doi.org/10.1088/0253-6102/35/6/651 - 17. Zeng, Y.B., Shao, Y.J. and Ma, W.X. (2002) Integral-Type Darboux Transformations for the mKdV Hierarchy with Self-Consistent Sources. Communications in Theoretical Physics, 38, 641-648.
http://dx.doi.org/10.1088/0253-6102/38/6/641 - 18. He, J.S., Zhang, L., Chen, Y. and Li, Y.S. (2006) Determinant Representation of Darboux Transformation for the AKNS System. Science in China Series A: Mathematics, 49, 1867-1878.
http://dx.doi.org/10.1007/s11425-006-2025-1 - 19. Zhou, Z.X. (2007) Darboux Transformations for Some Two Dimensional Affine Toda Equations. The International Congress of Chinese Mathematicians (ICCM), III, 405-416.
- 20. Wang, L., Gao, Y.T., Gai, X.L., Yu, X. and Sun, Z.Y. (2010) Vadermonde-Type Odd-Soliton Solutions for the Whitham-Broer-Kaup Model in the Shallow Water Small-Amplitude Regime. Journal of Nonlinear Mathematical Physics, 17, 197-211.
http://dx.doi.org/10.1142/S1402925110000714 - 21. Geng, X.G. and He, G.L. (2010) Darboux Transformation and Explicit Solutions for the Satsuma-Hirota Coupled Equation. Applied Mathematics and Computation, 216, 2628-2634.
http://dx.doi.org/10.1016/j.amc.2010.03.107 - 22. Xu, G.H. (2014) N-Fold Darboux Transformation of the Jaulent-Miodek Equation. Applied Mathematics, 5, 2657-2663.
http://dx.doi.org/10.4236/am.2014.517254
NOTES
*Corresponding author.

















































