Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:59715,11 pages
10.4236/jamp.2015.39140
A New Iterative Method for Multi-Moving Boundary Problems Based Boundary Integral Method
Kawther K. Al-Swat, Said G. Ahmed*
Department of Mathematics and Statistics, Faculty of Science, Taif University, Taif, Kingdom of Saudi Arabia
Email: *sgahmed911@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2015; accepted 15 September 2015; published 18 September 2015
ABSTRACT
The present paper deals with very important practical problems of wide range of applications. The main target of the present paper is to track all moving boundaries that appear throughout the whole process when dealing with multi-moving boundary problems continuously with time up to the end of the process with high accuracy and minimum number of iterations. A new numerical iterative scheme based the boundary integral equation method is developed to track the moving boundaries as well as compute all unknowns in the problem. Three practical applications, one for vaporization and two for ablation were solved and their results were compared with finite element, heat balance integral and the source and sink results and a good agreement were obtained.
Keywords:
Multi-Moving Boundary Problems, Vaporization Problem, Ablation Problem, Source and Sink Method, Finite Element Method, Heat Balance Integral Method, Boundary Integral Method

1. Introduction
The differential equation in a certain domain satisfying some given conditions is referred to as boundary-value problem. If one or more of the boundaries are not known and moving with time, the problem then is referred to as moving boundary problem [1] [2] . Furthermore, if the governing equation is time independent as well as the boundary condition, then the problem is referred to as free boundary problem [3] . Phase change problems are practical examples of free and moving boundary problems, frequently appear in industrial process and other problems of technological interests such as the determination of the depth of the frost or thaw penetration, designing of the roadway or other engineering works in cold regions and the so-called re-entry problem of hypersonic missiles in aeronautical science [4] [5] . When a body is exposed to heat flux the surface of the body changes phase, the changed phase is immediately removed upon formation. This is referred to ablation problem [6] . A major difference between Stefan and ablation problems is that the overall domain in Stefan problem remains fixed in space while the domain in the ablation problem is variable and diminishes in size with time. Numerical methods become more popular rather than analytical methods. Some of famous numerical methods are finite differences [7] , finite elements [8] , boundary elements [9] and more recent mesh-less (mesh-free) numerical methods [10] . In many aspects, the boundary integral equation method for solving boundary value problems proves to be advantageous over the conventional numerical methods. The present paper deals with very important practical problems of wide range of applications. The main target of the present paper is to track all moving boundaries that appear throughout the whole process when dealing with multi-moving boundary problems continuously with time up to the end of the process with high accuracy and minimum number of iterations. A new numerical iterative scheme based the boundary integral equation method is developed to track the moving boundaries as well as compute all unknowns in the problem.
2. Mathematical Model
A semi-infinite solid initially at uniform temperature with the following constraints, there is no sub cooling, no mushy zone, solid and liquid phases have equal and constant properties and finally no convection. The mathematical formulation consists of three different stages as follow:
Heating stage
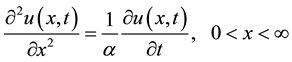 (1)
(1)
 (2)
(2)
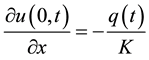 (3)
(3)
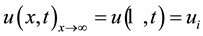 (4)
(4)
As 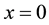 reaches the melting temperature, the second stage starts appearing.
reaches the melting temperature, the second stage starts appearing.
Liquid-solid stage
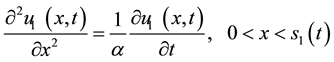 (5)
(5)
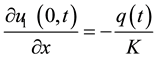 (6)
(6)
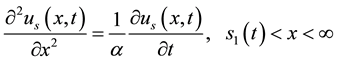 (7)
(7)
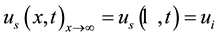 (8)
(8)
 (9)
(9)
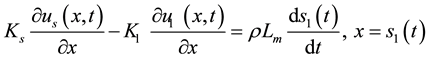 (10)
(10)
Gas-liquid-solid stage
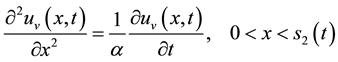 (11)
(11)
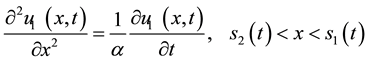 (12)
(12)
 (13)
(13)
 (14)
(14)
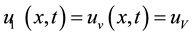 (15)
(15)


3. Boundary Integral Formulation
Starting by the weighted residual statement for diffusion equation as follows:
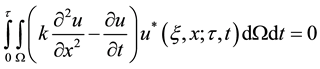
In Equation (18) 

In which, 
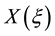

Integrating equation (18) twice by parts leads to:

For one-dimensional problems, Equation (20) takes the following form:

In Equation (21)


Making use of Equations (22) and (23) into Equation (20), the last one takes the following form:

For any point the integral equation takes the following form:

Discretization of Time
Equation (25) after the discretization of time takes the following form:

Assume that the potential u and the flux q are constant within each time step therefore Equation (26) can be written as:
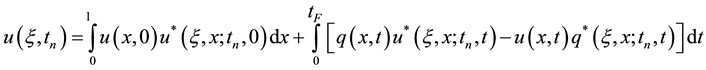
In Equation (27), we have two different time integrals, they are:
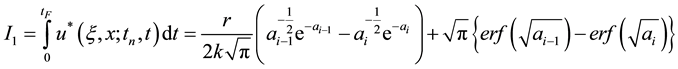
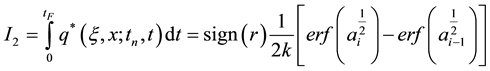
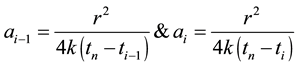
The domain integral

Now, the final form for the integral equation corresponding to the diffusion equation defined over fixed domain will be:

Similar procedure can be carried out taking into consideration the moving boundaries and their normal velocities, therefore and according to [11] [12] , and for the second and third stages, the integral equation corresponding to the diffusion equation with moving boundaries in a general final form will be:
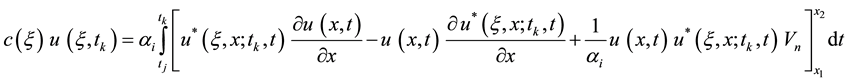
In Equation (33), 
in our case study, this velocity may be 
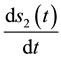
4. New Fixed-Moving-Fixed Algorithm
In the present paper, a generalized numerical algorithm and code for multi-moving boundary problem are developed, using visual Fortran 6.6. The main code consists of main program and three subroutines. The flow chart describing the main parts of the proposed algorithm is shown in Figure 1.
Figure 1. General fixed-moving-fixed integral algorithm.
4.1. Algorithm and Subroutine ONEPHASE
In this subroutine, a single phase bounded by two fixed boundaries are solved, using Equation (32) and the output will be the time at which melting starts and the corresponding location of the first moving boundary, separating the liquid and the solid,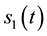
Suggested Algorithm
1) Input data, mold length

2) Apply the boundary integral equation, given by Equation (32) at the end points of the domain of interest to
estimate
3) Check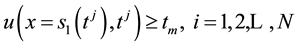
time of melting and the corresponding position for the moving boundary separating liquid and solid. If no update both the spatial and time variables 
4.2. Algorithm and Subroutine TWOPHASE
This subroutine concerns mainly with two phases each phase will be bounded by one fixed and the second is moving are solved and the output will be the time at which vapor starts and the corresponding location of the first and second moving boundaries 
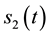
Suggested Algorithm
1) The input unit here is the output from one-phase subroutine.
2) Solve solid phase subjected to melting temperature at the moving boundary and initial temperature at the
fixed end to get
3) By knowing 
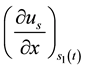
4) Check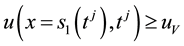
appearing with the new position of the moving boundary separating liquid/solid and the starting position of the second moving boundary separating vapor(gas)/liquid, if no update the moving boundary separating liquid/solid.
4.3. Algorithm and Subroutine THREEPHASE
This subroutine is for three phases, the first one is bounded by two boundaries, one fixed and one moving, the second phase is bounded by two moving boundaries, and the third phase is also bounded by two boundaries one fixed and one moving. The output of this subroutine is to track all moving boundaries, determination all unknowns in all phases up to the end of the process with minimum number of iterations and high prescribed accuracy. The flow chart of this subroutine is shown in Figure 2. In this figure, the absolute errors 
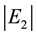


5. Numerical Results
5.1. Vaporization Test Problem
In this section, three test problems are solved to check the validity of the proposed algorithm and the high accuracy expected. The first example is a multi-moving boundary problem [13] . The thermo-physical properties are listed below in Table 1.
The solid material herein is of a low thermal conductivity and so the vaporization occurs before the moving boundary separating liquid and solid reaches the adiabatic boundary. The result due to the present algorithm is shown in Figure 3. In this figure, both vapor/liquid and liquid/solid moving boundaries are plotted both on the same figure. The liquid/solid moving boundary is in the left side, while the other one is on the right. From this figure, one can clearly determine the melting, vapor and the time at which the process ends. These times are determined and summarized in Table 2, at two different time steps. The absolute errors between the results due to the present method compared with the finite elements method are also presented in the same table. As we see, the absolute errors decrease by decreasing the time step. On the other hand by decreasing the time step, the number of iterations increases. The number of iterations are shown in Table 2, corresponding to the two time steps used. It is clear that the increase in the number of iterations is not so much but the accuracy improved to
Figure 2. Flow chart for THREEPHASE subroutine.
Figure 3. Moving boundaries location for vaporization test problem.
Table 1. Numerical data for vaporization test problem.
Table 2. Comparison between melting, vaporization and end time.
nearly the half.
5.2. Ablation Test Problem-1
A solid medium initially at uniform temperature, 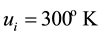

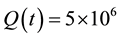
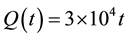
5.3. Ablation Test Problem-2
This problem is for a long enough solid mold initially at a uniform temperature. The surface 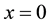

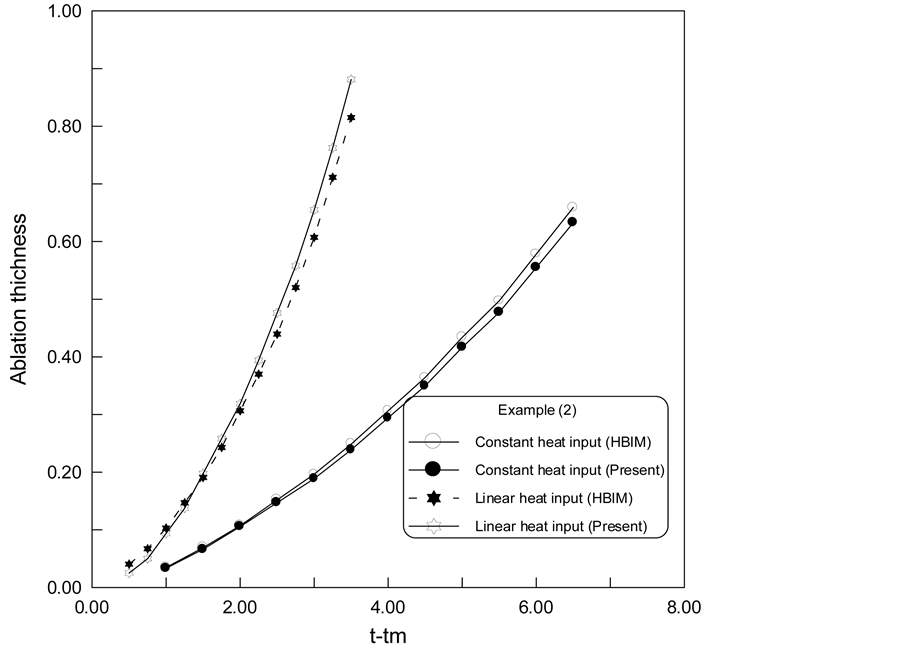
The ablation thickness due to the present method compared with the corresponding from the heat balance integral method is shown in Figure 7. It is clear that the ablation thickness is concave downward in both case of
Figure 4. Solid/liquid due to Constant heat flux-problem-1.
Figure 5. Ablated surface due to constant heat flux-problem-1.
Figure 6. Solid/liquid and Ablated surface due to linear heat flux-problem-1.
Figure 7. Ablation thickness for ablation test problem-2.
Table 3. Thermo-physical parameters.
input heat flux and at the same time, the ablation thickness in case of linear heat flux is higher than that for constant case. There is a good agreement between the two methods in both cases.
6. Conclusion
The importance of the present paper comes from its dealing with practical applications of wide range of our daily life. The boundary integral equation method is not so new but it is used as a mathematical tool due to its simplicity in use. Based on this method, a generalized numerical algorithm and computer code are developed to solve such applications. It is found from the computations that the developed algorithm and the code are so simple to handle and that an acceptable accuracy is obtained. Also by decreasing the time step, and a little bit increase of iterations, the absolute errors are decreased to the half nearly. Finally, the algorithm and subsequently the code can be easily modified to cover higher dimensional problems with acceptable accuracy, which can be improved by decreasing the time step, but on the other hand, stability should be achieved.
Cite this paper
Kawther K.Al-Swat,Said G.Ahmed, (2015) A New Iterative Method for Multi-Moving Boundary Problems Based Boundary Integral Method. Journal of Applied Mathematics and Physics,03,1126-1137. doi: 10.4236/jamp.2015.39140
References
- 1. Meaad, N.M.I. (2014) Mesh-Less Methods and Its Application to Free and Moving Boundary Problems. M.Sc. Thesis, Zagazig University, Zagazig. Supervision S. G. Ahmed.
- 2. Crank, J. (1984) Free and Moving Boundary Problems. Clarendon Press, Oxford.
- 3. Mohamd, N.A.E. (2002) Boundary Elements Methods and Its Non-Linear Analysis of Hydrofoils. Supervisors: Prof. S. G. Ahmed and Prof. A. F. Abd-Elgawad. Zagazig University, Zagazig.
- 4. Nofal, T.A. and Ahmed, S.G. (2015) An Integral Method to Solve Phase-Change Problems with/without Mushy Zones. Journal of Applied Mathematics and Mathematics, II, 152-157.
- 5. Ahmed, S.G. and Mekey, M.L. (2010) A Collocation and Cartesian Grid Methods Using New Radial Basis Function to Solve Class of Partial Differential Equations. International Journal of Computer Mathematics, 87, 1349-1362.
- 6. Meshrif, S.A. and Ahmed, S.G. (2007) Approximate Integral Method Applied to Ablation Problem in a Finite Slab. International Symposium on Recent Advances in Mathematics and Its Applications (ISRAMA 2007), Culcutta, 15-17 December 2007, 1-12.
- 7. Zerroukat, M. and Chatwin, C.R. (1994) Computational Moving and Boundary Problems. Research Studies Press Ltd., Baldock.
- 8. Ruan, Y. and Zabaras, N. (1991) An Inverse Finite Element Technique to Determine The change of Phase Interface Location in Two-Dimensional Melting Problem. Communications in Applied Numerical Methods, 7, 325-338.
http://dx.doi.org/10.1002/cnm.1630070411 - 9. Mohamed, W.A. (2012) Advanced Mathematical Analysis for Phase Change Problems with and without Mushy Zones. Supervisors: Prof. S. G. Ahmed and Prof. M. E. Mohamed. Zagazig University, Zagazig.
- 10. Liu, W., Chen, Y., Jun, S., Chen, J.-S., Belytschko, T., Pan, C., Uras, R. and Chang, C. (1996) Overview and Application of the Reproducing Kernel Particle Methods. Archive of Computational Methods in Engineering: State of the Art Reviews, 3, 3-80.
http://dx.doi.org/10.1007/BF02736130 - 11. Ahmed, S.G. (2005) A New Algorithm for Moving Boundary Problems Subject to Periodic Boundary Conditions. International Journal of Numerical Methods for Heat and Fluid Flow, 16, 18-27.
- 12. Abd-El Fatah, W.M. and Ahmed, S.G. (2006) Boundary Integral Formulation for Binary Alloys from a Cooling Solid Wall. International Journal of Computational and Applied Mathematics, 5, 687-696.
- 13. Ahmed, S.G. (2003) A New Algorithm for Front Tracking of Ablation Problem in Unbounded Domain. Ain Shams University, Egypt.
- 14. Mehdi, A. and Hsieh, C.K. (1994) Solution of Ablation and Combination of Ablation and Stefan Problems by a Source and Sink Method. Numerical Heat Transfer, Part A, 26, 67-86.
http://dx.doi.org/10.1080/10407789408955981 - 15. Ahmed, S.G. (2003) A Numerical Solution for Nonlinear Heat Flow Problem Using Boundary Integral Method. 6th International Conference of Computer Methods and Experimental Measurements for Surface Treatment, Crete, March 2003.
Nomenclature










Subscript



NOTES
*Corresponding author.