Journal of Applied Mathematics and Physics
Vol.03 No.06(2015), Article ID:57622,5 pages
10.4236/jamp.2015.36082
A Note on Discontinuous Functions with Continuous Second Iterate
Pingping Zhang1, Xiaobing Gong2
1Department of Mathematics, Binzhou University, Shandong, China
2Department of Mathematics, Neijiang Normal University, Sichuan, China
Email: zhangpingpingmath@163.com, xbgong@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 May 2015; accepted 26 June 2015; published 30 June 2015
ABSTRACT
This paper investigates four classes of functions with a single discontinuous point. We give the sufficient and necessary conditions under which the second order iterates are continuous functions. Furthermore, the sufficient conditions for the continuity of the even order iterates with finitely many discontinuous points are obtained.
Keywords:
Iteration, Discontinuous Point, Continuous Function

1. Introduction
For a nonempty set X and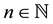 , the n-th iterate of a self-mapping
, the n-th iterate of a self-mapping 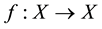 is defined by
is defined by 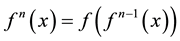 and
and 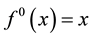 for all
for all 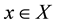 inductively. As a nonlinear operator, iteration usually amplifies the complexity
inductively. As a nonlinear operator, iteration usually amplifies the complexity
of functions [1] - [7] , computing the n-th iterate of functions is complicated, even for simple functions (see [8] - [12] ). On the other hand, iteration can turn complex functions into simple ones. Recently, the following problem was first formulated by X. Liu, L. Liu and W. Zhang: what are discontinuous functions whose iterates of a certain order are continuous? This question, together with three classes of discontinuous functions defined on compact interval, was answered in the affirmative in [13] . That is, suppose that 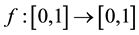 with a single discontinuous point (removable discontinuous point, jumping discontinuous or oscillating discontinuous), the authors respectively gave the sufficient and necessary conditions under which the second order iterates are continuous functions.
with a single discontinuous point (removable discontinuous point, jumping discontinuous or oscillating discontinuous), the authors respectively gave the sufficient and necessary conditions under which the second order iterates are continuous functions.
The purpose of this paper is to study the discontinuous functions defined on open interval. For four classes of discontinuous functions with unique discontinuous point, we obtain the sufficient and necessary conditions for functions being continuous ones under second iterate, which are easily verified respectively. As corollaries, the sufficient conditions for the continuity of the even order iterates with finitely many discontinuous points are obtained. Our results are illustrated by examples in Section 3 .
2. Main Results
In this section the main results for the continuity of 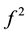 are stated. Throughout the paper we let
are stated. Throughout the paper we let 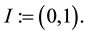
Theorem 1. Suppose that 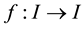 has unique removable discontinuous point
has unique removable discontinuous point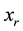 . Let
. Let
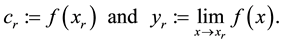 (1)
(1)
Then 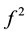 is continuous on I if and only if the following conditions are fulfilled:
is continuous on I if and only if the following conditions are fulfilled:
(A1) 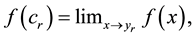
(A2)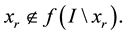
Proof. (Þ) Assume that 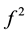 is continuous on I, the removable discontinuous point
is continuous on I, the removable discontinuous point 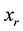 of f is continuous point of
of f is continuous point of 


On the other hand, using the definition of 


Thus (2) and (3) lead to (A1). For an indirect proof of (A2), assume that 

which contradicts the continuity of 
(Ü) It follows from (A1)
implying that 




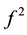
Corollary 1. Suppose that 

(
(
are fulfilled for all 



Proof. By using the sufficiency of Theorem 1, the assumption (





Thus 


Theorem 2. Suppose that 


Then 
(B1)
(B2)
Proof. (Þ) In view of the definitions of 


and

Clearly, (4) and (5) yield (B1). Suppose the contrary to (ii), there is 

is nonexistence since 


(Ü) The condition (B1) implies

and

Thus, (6) and (7) lead to
which implies that the jumping discontinuous point 




Corollary 2. Suppose that 

(
(
are fulfilled for all 




Proof. The discussion is similar as that of Corollary 1. By using the sufficiency of Theorem 2, the assumption (








Theorem 3. Suppose that 


(C1) 

(C2)
Proof. (Þ) We first show that the condition (C1) holds. Suppose the contrary, for any 
corresponding point 







contradiction. This gives a proof to (C1). To prove (C2), by reduction to absurdity, we assume that 



is nothingness, which contradicts the continuity of
(Ü) From the assumption (C1) we see that
implying the oscillating discontinuous point 



Corollary 3. Suppose that 

(


(
are fulfilled for all

Proof. The discussion is similar as that of Corollary 1. By using the sufficiency of Theorem 3, the second iterate 







Theorem 4. Suppose that 



(D1)
(D2)
Proof. (Þ) Note that 



which shows the limit 




is infinite, which contradicts the continuity of
(Ü) From the assumption (D1) and the fact 
implying the infinite discontinuous point 



Corollary 4. Suppose that 




(
(
Proceeding similarly as Theorem 4 one can show this corollary.
Corollary 5. Suppose that 

(
(
are fulfilled for all 


Proof. We obtain the result by using the similar argument as Corollary 1. In view of the sufficiency of Theorem 4, the second iterate 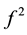


all points 




3. Examples
In this section we demonstrate our theorems with examples.
Example 1. Consider the mapping 
Clearly, 

Moreover, the set 


Example 2. Consider the mapping 
Clearly, 

and 


Example 3. Consider the mapping 
Clearly, 






Example 4. Consider the mapping 
Clearly, 
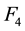
and 


Acknowledgements
We thank the Editor and the referee for their comments. Project supported by Shandong Provincial Natural Science Foundation of China (ZR2014AL003), Scientific Research Fund of Sichuan Provincial Education Departments (12ZA086), Scientific Research Fund of Shandong Provincial Education Department (J12L59) and Doctoral Fund of Binzhou University (2013Y04).
References
- Lesmoir-Gordon, N. and Edney, W. (2006) Introducing Fractal Geometry. Icon Books, Cambridge.
- Lesmoir-Gordon, N. (2010) The Colours of Infinity: The Beauty and Power of Fractals. Springer, London. http://dx.doi.org/10.1007/978-1-84996-486-9
- Mandelbrot, B. (2004) Fractals and Chaos: The Mandelbrot Set and Beyond. Springer, New York. http://dx.doi.org/10.1007/978-1-4757-4017-2
- Zhang, P.P. (2012) Formal and Analytic Solutions for a Quadric Iterative Functional Equation. Electronic Journal of Differential Equations, 46, 1-9.
- Zhang, P. and Gong, X. (2014) Existence of Solutions for Iterative Differential Equaitons. Electronic Journal of Differential Equations, 7, 1-10.
- Zhang, P. and Mi, L. (2009) Analytic Solutions of a Second Order Iterative Functional Differential Equation. Applied Mathematics and Computation, 210, 277-283. http://dx.doi.org/10.1016/j.amc.2008.12.007
- Zhang, P. and Zhang, Q. (2010) Local Invertible Analytic Solutions of a First Order Iterative Functional Differential Equation. Acta Mathematica Sinica Chinese Series, 53, 409-416.
- Sun, D. (2004) Iteration of Quasi-Polynomial of Degree Two (in Chinese). J. Math., 24, 237-240.
- Targonski, G. (1981) Topics in Iterative Theory. Vandenhoeck and Ruprecht, Götingen.
- Wu, Z. and Sun, D. (2006) The Iteration of Quasi-Polynomials mappings (in Chinese). Acta Math. Sci. A., 26, 493-497.
- Xu, L. and Xu, S. (2006) On Iteratio of Linear Fractional Function and Applications (in Chinese). Math. Pract. Theory., 36, 225-228.
- Yu, Z., Yang, L. and Zhang, W. (2012) Discussion on Polynomials Having Polynomial Iterative Roots. Journal of Symbolic Computation, 47, 1154-1162. http://dx.doi.org/10.1016/j.jsc.2011.12.038
- Liu, X., Liu, L. and Zhang, W. Discontinuous Function with Continuous Second Iterate. Aequat. Math.




































