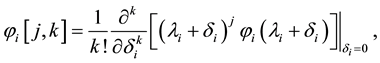Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56541,6 pages
10.4236/jamp.2015.35065
Generalized Darboux Transformation and Rational Solutions for the Nonlocal Nonlinear Schrödinger Equation with the Self-Induced Parity-Time Symmetric Potential
Jian Chen
College of Science, University of Shanghai for Science and Technology, Shanghai, China
Email: chen978918050@163.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 April 2015; accepted 19 May 2015; published 22 May 2015
ABSTRACT
In this paper, I construct a generalized Darboux transformation for the nonlocal nonlinear Schrö- dinger equation with the self-induced parity-time symmetric potential. The N-order rational solution is derived by the iterative rule and it can be expressed by the determinant form. In particular, I calculate first-order and second-order rational solutions and obtain their figures according to different parameters.
Keywords:
Generalized Darboux Transformation, Rational Solutions, Nonlocal Nonlinear Schrödinger Equation

1. Introduction
Parity-time (PT) symmetry was firstly proposed by Bender and Boettcher in quantum mechanics [1] . And it has been widespread concerned in optical solitons [2] , non-reciprocal light propagation [3] , unidirectional invisibility [4] , perfect absorber [5] and so on. Since then, there has been attracted more and more attentions in the non- Hermitian systems with PT symmetry [6] -[13] . Generally, the non-Hermitian Hamiltonian  is deemed to be PT symmetric if
is deemed to be PT symmetric if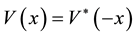 , where
, where 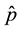 denotes the momentum operator;
denotes the momentum operator;  is the complex potential [1] [6] ; the asterisk denotes the complex conjugate. According to the PT symmetry condition, the real part of a PT symmetry complex potential must be an even function whereas the imaginary part should be odd. In optical system, the PT symmetric potential can be realized by controlling the complex refractive index distribution
is the complex potential [1] [6] ; the asterisk denotes the complex conjugate. According to the PT symmetry condition, the real part of a PT symmetry complex potential must be an even function whereas the imaginary part should be odd. In optical system, the PT symmetric potential can be realized by controlling the complex refractive index distribution 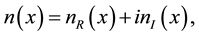 where the refractive index profile
where the refractive index profile 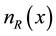 is an even function in the trans- verse direction, the gain or loss component
is an even function in the trans- verse direction, the gain or loss component 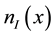 is an odd one [10] -[12] .
is an odd one [10] -[12] .
In the nonlinear optics, the PT symmetric and Kerr nonlinearity linear potentials have been intensively researched in the nonlinear Schrödinger (NLS) equations. For example, [14] has studied the soliton in PT symmetric potential with competing nonlinearity; [15] has studied the dynamical behaviors of 2D nonautonomous solitons in PT symmetric potentials; and [16] has studied stable dark solitons in PT symmetric dual-core waveguides.
In this paper, I will consider a nonlocal NLS equation [17]
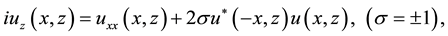 (1)
(1)
which is non-Hermitian but PT symmetric, where 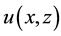 is a complex valued function of real variables x and z, and
is a complex valued function of real variables x and z, and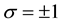 . The signs
. The signs 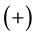 and
and  denote the focusing and defocusing respectively. In Equation (1), the nonlinear term brings a self-induced potential of the form
denote the focusing and defocusing respectively. In Equation (1), the nonlinear term brings a self-induced potential of the form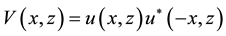 , which satisfies the PT symmetric condition
, which satisfies the PT symmetric condition 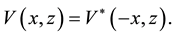 The exact moving one-soliton solution of Equation (1) has been obtained in [17] via the inverse scattering transform. The dark and antidark soliton interactions have been given in [18] via the classical Darboux transformation (DT) method. However, there are no papers on high-order rational solutions of Equation (1) by generalized Darboux transformation (gDT).
The exact moving one-soliton solution of Equation (1) has been obtained in [17] via the inverse scattering transform. The dark and antidark soliton interactions have been given in [18] via the classical Darboux transformation (DT) method. However, there are no papers on high-order rational solutions of Equation (1) by generalized Darboux transformation (gDT).
The organization of this paper is as follows: In Section 2, a determinant expression of N-order gDT will be constructed based on the Lax pair. In Section 3, I will obtain a general determinant expression of N-order rational solution of Equation (1). In addition, I calculate first-order and second-order rational solutions and obtain their figures according to different parameters. The conclusions will be given in Section 4.
2. Lax Pair and Generalized Darboux Transformation
The Lax pair of Equation (1) can be expressed as follows [17] :
 (2)
(2)
where 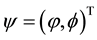 is the vector eigenfunction of Lax pair (2), and T signifies the vector transpose. Matrices U and V have the following forms:
is the vector eigenfunction of Lax pair (2), and T signifies the vector transpose. Matrices U and V have the following forms:
where 

The classical DT for Equation (1) has been constructed in [18] :

where
Here 




choose different eigenfunctions 

Next, I suppose 


where
In the following, I derive the determinant form of the gDT for Equation (1). Considering N different eigenfunctions 

where
Thus, on the basis of the work in [20] [21] , I can perform the limit on Formula (4), then obtain the following result:

where
3. Rational Solutions
To construct the rational solutions of Equation (1), I take a plane wave solution

where a is real constant, and the frequency 

Then inserting Equation (7) into the Lax pair (2) and taking

with
where 






where
The relevant Taylor expansions are
where
It follows that the N-order rational solution for Equation (1), reads

where
Setting N = 1 in Formula (10), then I obtain the first-order rational solution (see Figure 1(a)) with the parameters


Then with N = 2, the second-order rational solution (see Figure 1(b)) with the parameters
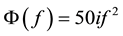

Figure 1. (a) Plot of the first-order rational solution; (b) Plot of the second-order rational solution.
where
4. Conclusion
In this paper, I have studied the nonlocal nonlinear Schrödinger equation with the self-induced parity-time- symmetric potential. Then I have constructed a gDT for Equation (1) and derived the N-fold rational solutions in determinant forms. In particular, I have calculated first-order and second-order rational solutions from a planewave solution and obtained their figures according to different parameters.
Acknowledgements
This work is supported by the Shanghai Leading Academic Discipline Project under Grant No. XTKX2012, by the Natural Science Foundation of Shanghai under Grant No. 12ZR1446800, Science and Technology Commission of Shanghai municipality, and by the National Natural Science Foundation of China under Grant Nos. 11201302 and11171220.
References
- Bender, C.M. and Boettcher, S. (1998) Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Physical Review Letters, 80, 5243. http://dx.doi.org/10.1103/PhysRevLett.80.5243
- Musslimani, Z.H., Makris, K.G., El-Ganainy, R. and Christodoulides, D.N. (2008) Optical Solitons in PT Periodic Potentials. Physical Review Letters, 100, Article ID: 030402. http://dx.doi.org/10.1103/PhysRevLett.100.030402
- Makris, K.G., El-Ganainy, R., Christodoulides, D.N. and Musslimani, Z.H. (2008) Beam Dynamics in PT Symmetric Optical Lattices. Physical Review Letters, 100, Article ID: 103904. http://dx.doi.org/10.1103/PhysRevLett.100.103904
- Lin, Z., Ramezani, H., Eichelkraut, T., Kottos, T., Cao, H. and Christodoulides, D.N. (2011) Unidirectional Invisibility Induced by PT-Symmetric Periodic Structures. Physical Review Letters, 106, Article ID: 213901. http://dx.doi.org/10.1103/PhysRevLett.106.213901
- Chong, Y.D., Ge, L. and Stone, A.D. (2011) PT-Symmetry Breaking and Laser-Absorber Modes in Optical Scattering Systems. Physical Review Letters, 106, Article ID: 093902. http://dx.doi.org/10.1103/physrevlett.106.093902
- Bender, C.M. (2007) Making Sense of Non-Hermitian Hamiltonians. Reports on Progress in Physics, 70, 947-1018. http://dx.doi.org/10.1088/0034-4885/70/6/R03
- Bender, C.M., Brody, D.C., Jones, H.F. and Meister, B.K. (2007) Faster than Hermitian Quantum Mechanics. Physical Review Letters, 98, Article ID: 040403. http://dx.doi.org/10.1103/physrevlett.98.040403
- Ghatak, A., Mandal, R.D.R. and Mandal, B.P. (2013) Various Scattering Properties of a New PT-Symmetric Non-Her- mitian Potential. Annals of Physics, 336, 540-552. http://dx.doi.org/10.1016/j.aop.2013.06.008
- Miroshnichenko, A.E., Malomed, B.A. and Kivshar, Y.S. (2011) Nonlinearly-PT-Symmetric Systems: Spontaneous Symmetry Breaking and Transmission Resonances. Physical Review A, 84, 911-916. http://dx.doi.org/10.1103/PhysRevA.84.012123
- Christodoulides, D.N., Lederer, F. and Silberberg, Y. (2003) Review Article Discretizing Light Behaviour in Linear and Nonlinear Waveguide Lattices. Nature, 424, 817-823. http://dx.doi.org/10.1038/nature01936
- Rüter, C.E., Makris, K.G., El-Ganainy, R., Christodoulides, D.N., Segev, M. and Kip, D. (2010) Observation of Parity- Time Symmetry in Optics. Nature Physics, 6, 192-195. http://dx.doi.org/10.1038/nphys1515
- El-Ganainy, R., Makris, K.G., Christodoulides, D.N. and Musslimani, Z.H. (2007) Theory of Coupled Optical PT- Symmetric Structures. Optics Letters, 32, 2632-2634. http://dx.doi.org/10.1364/OL.32.002632
- Dai, C.Q., Xu, Y.G. and Wang, Y. (2015) Nonautonomous Cnoidal Wave and Soliton Management in Parity-Time Symmetric Potentials. Communications in Nonlinear Science and Numerical Simulation, 20, 389-400. http://dx.doi.org/10.1016/j.cnsns.2014.06.004
- Khare, A., Al-Marzoug, S.M. and Bahlouli, H. (2012) Solitons in PT-Symmetric Potential with Competing Nonlinearity. Physics Letters A, 376, 2880-2886. http://dx.doi.org/10.1016/j.physleta.2012.09.047
- Dai, C.Q. and Wang, Y.Y. (2014) Nonautonomous Solitons in Parity-Time Symmetric Potentials. Optics Communications, 315, 303-309. http://dx.doi.org/10.1016/j.optcom.2013.11.030
- Bludov, Y.V., Konotop, V.V. and Malomed, B.A. (2013) Stable Dark Solitons in PT-Symmetric Dual-Core Waveguides. Physical Review A, 87, Article ID: 013816. http://dx.doi.org/10.1103/PhysRevA.87.013816
- Ablowitz, M.J. and Musslimani, Z.H. (2013) Integrable Nonlocal Nonlinear Schrödinger Equation. Physical Review Letters, 110, Article ID: 064105. http://dx.doi.org/10.1103/PhysRevLett.110.064105
- Li, M. and Xu, T. (2015) Dark and Antidark Soliton Interactions in the Nonlocal Nonlinear Schrödinger Equation with the Self-Induced Parity-Time-Symmetric Potential. Physical Review E, 91, Article ID: 033202. http://dx.doi.org/10.1103/PhysRevE.91.033202
- Matveev, V.B. and Salle, M. (1991) Darboux Transformations and Solitons. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-00922-2
- Guo, B.L., Ling, L.M. and Liu, Q.P. (2012) Nonlinear Schrödinger Equation: Generalized Darboux Transformation and Rogue Wave Solutions. Physical Review E, 85, Article ID: 026607. http://dx.doi.org/10.1103/PhysRevE.85.026607
- Yang, B., Zhang, W.G., Zhang, H.Q. and Pei, S.B. (2013) Generalized Darboux Transformation and Rogue Wave Solutions for the Higher-Order Dispersive Nonlinear Schrödinger Equation. Physica Scripta, 88, Article ID: 065004. http://dx.doi.org/10.1088/0031-8949/88/06/065004