Journal of Applied Mathematics and Physics
Vol.03 No.03(2015), Article ID:55179,18 pages
10.4236/jamp.2015.33048
New Scenario for Transition to Slow 3-D Turbulence
Jaykov Foukzon
Department of Mathematic, Israel Institute of Technology, Haifa, Israel
Email: jaykovfoukzon@list.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2015; accepted 26 March 2015; published 30 March 2015
ABSTRACT
Analytical non-perturbative study of the three-dimensional nonlinear stochastic partial differential equation with additive thermal noise, analogous to that proposed by V. N. Nikolaevskii [1] -[5] to describe longitudinal seismic waves, is presented. The equation has a threshold of short-wave instability and symmetry, providing long wave dynamics. New mechanism of quantum chaos generating in nonlinear dynamical systems with infinite number of degrees of freedom is proposed. The hypothesis is said, that physical turbulence could be identified with quantum chaos of considered type. It is shown that the additive thermal noise destabilizes dramatically the ground state of the Nikolaevskii system thus causing it to make a direct transition from a spatially uniform to a turbulent state.
Keywords:
3D Turbulence, Chaos, Quantum Chaos, Additive Thermal Noise, Nikolaevskii System

1. Introduction
In the present work a non-perturbative analytical approach to the studying of problem of quantum chaos in dynamical systems with infinite number of degrees of freedom is proposed. Statistical descriptions of dynamical chaos and investigations of noise effects on chaotic regimes are studied. Proposed approach also allows estimate the influence of additive (thermal) fluctuations on the processes of formation of developed turbulence modes in essentially nonlinear processes like electro-convection and other. A principal role the influence of thermal fluctuations on the dynamics of some types of dissipative systems in the approximate environs of derivation rapid of a short-wave instability was ascertained. Impotent physical results follows from Theorem 2, is illustrated by example of 3D stochastic model system:
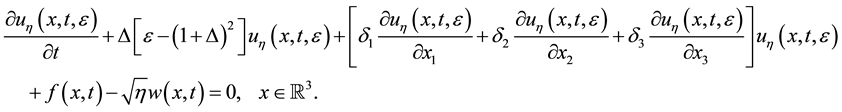 (1.1)
(1.1)
 , (1.2)
, (1.2)
which was obtained from the non-stochastic 3D Nikolaevskii model:
 (1.3)
(1.3)
which is perturbed by additive “small” white noise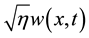 . And analytical result also illustrated by example of 1D stochastic model system
. And analytical result also illustrated by example of 1D stochastic model system
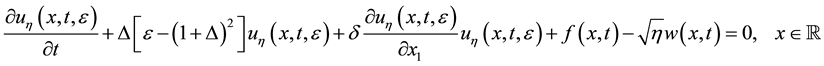 (1.4)
(1.4)
 (1.5)
(1.5)
which was obtained from the non-stochastic 1D Nikolaevskiis model:
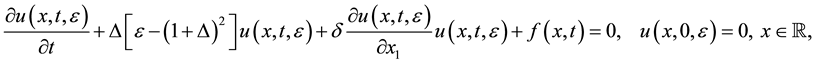 (1.6)
(1.6)
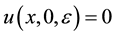 . (1.7)
. (1.7)
Systematic study of a different type of chaos at onset “soft-mode turbulence” based on numerical integration of the simplest 1D Nikolaevskii model (1.7) has been executed by many authors [2] -[7] . There is an erroneous belief that such numerical integration gives a powerful analysis is means of the processes of turbulence conception, based on the classical theory of chaos of the finite-dimensional classical systems [8] -[11] .
Remark 1.1. However, as it well known, such approximations correct only in a phase of turbulence conception, when relatively small number of the degrees of freedom excites. In general case, when a very large number of the degrees of freedom excites, well known phenomena of the numerically induced chaos, can to spoils in the uncontrollable way any numerical integration [12] -[15] .
Remark 1.2. Other non-trivial problem stays from noise round off error in computer computation using floating point arithmetic [16] -[20] . In any computer simulation the numerical solution is fraught with truncation by round off errors introduced by finite-precision calculation of trajectories of dynamical systems, where round off errors or other noise can introduce new behavior and this problem is a very more pronounced in the case of chaotic dynamical systems, because the trajectories of such systems exhibit extensive dependence on initial conditions. As a result, a small random truncation or round off error, made computational error at any step of computation will tend to be large magnified by future computational of the system [17] .
Remark 1.3. As it well known, if the digitized or rounded quantity is allowed to occupy the nearest of a large number of levels whose smallest separation is E0, then, provided that the original quantity is large compared to E0 and is reasonably well behaved, the effect of the quantization or rounding may betreated as additive random noise [18] . Bennett has shown that such additive noise is nearly white, with mean squared value of  [19] . However the complete uniform white-noise model to be valid in the sense of weak convergence of probabilistic measures as the lattice step tends to zero if the matrices of realization of the system in the state space satisfy certain nonresonance conditions and the finite-dimensional distributions of the input signal are absolutely continuous [21] [22] .
[19] . However the complete uniform white-noise model to be valid in the sense of weak convergence of probabilistic measures as the lattice step tends to zero if the matrices of realization of the system in the state space satisfy certain nonresonance conditions and the finite-dimensional distributions of the input signal are absolutely continuous [21] [22] .
The method deprived of these essential lacks in general case has been offered by the author in papers [23] - [27] .
Remark 1.4. Thus from consideration above it is clear that numerical integration procedure of the 1D Nikolaevskii model (1.6)-(1.7) executed in papers [2] -[7] in fact dealing with stochastic model (1.4)-(1.5).
There is an erroneous the point of view, that a white noise with enough small intensity does not bring any significant contributions in turbulent modes, see for example [3] . By this wrong assumptions the results of the numerical integration procedure of the 1D Nikolaevskii model (1.6)-(1.7) were mistakenly considered and interpreted as a very exact modeling the slow turbulence within purely non stochastic Nikolaevskii model (1.6)-(1.7). Accordingly wrong conclusions about that temperature noises does not influence slow turbulence have been proposed in [3] . However, in [27] has shown non-perturbatively that a white noise with enough small intensity can to bring significant contributions in turbulent modes and even to change this modes dramatically.
At the present time it is generally recognized that turbulence in its developed phase has essentially singular spatially-temporal structure. Such as in gular conduct is impossible to describe adequately by the means of some model system of equations of a finite dimensionality. In this point a classical theory of chaos is able to describe only small part of turbulence phenomenon in liquid and another analogous of dynamical systems. The results of non-perturbative modeling of super-chaotic modes, obtained in the present paper allow us to put out a quite probable hypothesis: developed turbulence in the real physical systems with infinite number of degrees of freedom is a quantum super-chaos, at that the quantitative characteristics of this super-chaos, is completely determined by non-perturbative contribution of additive (thermal) fluctuations in the corresponding classical system dynamics [18] -[20] .
2. Main Theoretical Results
We study the stochastic r-dimensional differential equation analogous proposed by Nikolaevskii [1] to describe longitudinal seismic waves:
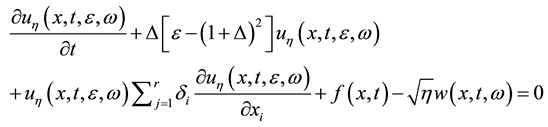 (2.1)
(2.1)
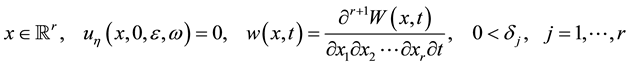 (2.2)
(2.2)
The main difficulty with the stochastic Nikolaevskii equation is that the solutions do not take values in a function space but in generalized function space. Thus it is necessary to give meaning to the non-linear terms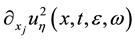 ,
, 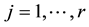 because the usual product makes no sense for arbitrary distributions. We deal with product of distributions via regularizations, i.e., we approximate the distributions by appropriate way and pass to the limit. In this paper we use the approximation of the distributions by approach of Colombeau generalized func- tions [28] .
because the usual product makes no sense for arbitrary distributions. We deal with product of distributions via regularizations, i.e., we approximate the distributions by appropriate way and pass to the limit. In this paper we use the approximation of the distributions by approach of Colombeau generalized func- tions [28] .
Notation 2.1.We denote by 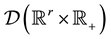 the space of the infinitely differentiable functions with compact supportin
the space of the infinitely differentiable functions with compact supportin 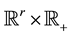 and by
and by  its dual space. Let
its dual space. Let 



Definition 2.1. [29] . We say that a random field 





Definition 2.2. We say that that 


1) 


2) 

3) for all
4)
5) 

However, in this paper we use the solutions of stochastic Nikolaevskii equation only in the sense of Colombeau generalized functions [30] .
Remark 2.1. Note that from Definition 2.2 it is clear that any strong generalized solution 
By formula (#) one can to define appropriate generalized solution of Equations (2.1)-(2.2) even if a strong generalized solution of Equations (2.1)-(2.2) does not exist.
Definition 2.3. Assume that a strong generalized solution of Equations (2.1)-(2.2) does not exist. We shall say that:
1) Colombeau generalized stochastic process 

a)
b) 

2) Colombeau generalized stochastic process 

a)
b) 

Notation 2.2. [30] . The algebra of moderate element we denote by

Notation 2.3. [30] . We shall use the following designations. If 





Definition 2.4. [30] . Let 


Let 


1) for fixed 


2) almost surely in


Notation 2.3. [30] . The Colombeau algebra of Colombeau random generalized function is denoted by
Definition 2.5. Let 




3) 

4) Smooth with respect to 
5) Also
6) Therefore 

7) In this way we have an imbedding
Definition 2.6. Denote by 





for all

such that: 1)


Viewed as a Colombeau random generalized function, it has a representative (denoting on variables in 





Definition 2.7. Smoothed with respect to 






Theorem 2.1. [25] . (Large Deviation Principle for SPDE) (I) Let



Here: 1) 

2)
3) 

(II) Let




Here Equations (2.5)-(2.7) is obtained from Equations (2.3)-(2.4) by spatial discretization on finite lattice 



(III) Assume that Colombeau-Ito’s SDE (2.5)-(2.7) is a strongly dissipative [26] .
(IV) Let 


Then

Proof. The proof based on Strong Large Deviations Principles (SLDP-Theorem) for Colombeau-Ito’s solution of the Colombeau-Ito’s SDE, see [26] , Theorem 6. By SLDP-Theorem one obtain directly the differential master equation (see [26] , Equation (90)) for Colombeau-Ito’s SDE (2.5)-(2.7):


We set now 


From Equations (2.5)-(2.7) and Equations (2.13)-(2.14) by SLDP-Theorem (see see [26] , inequality (89)) we obtain the inequality

Let us consider now the identity

From the identity (2.16) by integration we obtain the identity

From the identity (2.17) by using the triangle inequality we obtain the inequality

From the inequality (2.18) by the inequality (2.15) for all 

In the limit 
In the limit 

We note that

Therefore from (2.20) and (2.21) we obtain the inequality

In the limit 




Therefore from the inequality (2.22) follows the inequality

In the limit 

From the inequality (2.25) one obtain the inequality

From the inequality (2.27) and Equation (2.26) finally we obtain the inequality

The inequality (2.28) finalized the proof.
Definition 2.7. (The Differential Master Equation) The linear PDE:


we will call as the differential master equation.
Definition 2.8. (The Transcendental Master Equation) The transcendental equation

we will call as the transcendental master equation.
Remark 2.2. We note that concrete structure of the Nikolaevskii chaos is determined by the solutions 

3. Criterion of the Existence Quantum Chaos in Euclidian Quantum N-Model
Definition 3.1. Let 




Then we will say that a function 
Definition 3.2. Assume that there exist a set 


i.e., 

Then we will say that Euclidian quantum N-model has the quasi-determined Euclidian quantum chaos (QD- quantum chaos).
Definition 3.3. For each point 


Definition 3.4. Assume that Euclidian quantum N-model (2.1) has the Euclidian QD-quantum chaos.
For each point 


We will say that the set-valued function 
Theorem 3.1. Assume that 







Definition 3.5. For each point 
Figure 1. Evolution of QD-chaotic solution 






Figure 2. The spatial structure of QD-chaotic solution 




1)
2)
3)
Definition 3.7.
1) Function 
2) Function 
3) Function 

Definition 3.8. Assume now that

Then we will say that Euclidian quantum N-model has QD-quantum chaos of the asymptotically finite width at point
Definition 3.9. Assume now that

Then we will say that Euclidian quantum N-model has QD-quantum chaos of the asymptotically infinite width at point 
Definition 3.10. For each point 
1)
2)
3)
Theorem 3.2. For each point 

Proof. Immediately follows by Theorem 2.1 and Definitions 3.5, 3.10.
Theorem 3.3. (Criterion of QD-quantum chaos in Euclidian quantum N-model)
Assume that

Then Euclidian quantum N-model has QD-quantum chaos.
Proof. Immediately follows by the Inequality (3.7) and Definition 3.2.
Figure 3. The QD-quantum chaos of the asymptotically infinite width at point




Figure 4. The fine structure of the QD-quantum chaos of the asymptotically infinite width at point x = 3, 




4. Quasi-Determined Quantum Chaos and Physical Turbulence Nature
In generally accepted at the present time hypothesis what physical turbulence in the dynamical systems with an infinite number of degrees of freedom really is, the physical turbulence is associated with a strange attractors, on which the phase trajectories of dynamical system reveal the known properties of stochasticity: a very high dependence on the initial conditions, which is associated with exponential dispersion of the initially close trajectories and brings to their non-reproduction; everywhere the density on the attractor almost of all the trajectories a very fast decrease of local auto-correlation function [2] -[9]

Here
In contrast with canonical numerical simulation, by using Theorem 2.1 it is possible to study non-perturba- tively the influence of thermal additive fluctuations on classical dynamics, which in the considered case is described by Equation (4.1).
The physical nature of quasi-determined chaos is simple and mathematically is associated with discontinuously of the trajectories of the stochastic process 

In order to obtain the characteristics of this turbulence, which is a very similarly to local auto-correlation function (3.1) we define bellow some appropriate functions.
Definition 4.1. The numbering function 

Here by 
Definition 4.2. Assume now that a set 




Definition 3.3. The mean value function 



Definition 3.4. The turbulent pulsations function 



Definition 3.5. The local auto-correlation function is defined by


Definition 3.6. The normalized local auto-correlation function is defined by

Let us consider now 1D Euclidian quantum N-model corresponding to classical dynamics

Corresponding Langevin equation are [34] [35] :


Corresponding differential master Equations (2.29)-(2.30) are


Corresponding transcendental master Equation (2.31) are


We assume now that



The result of calculation using transcendental master Equation (4.15) the corresponding function 
The result of calculation using master Equation (4.13) the corresponding function 
Let us calculate now corresponding normalized local auto-correlation function
Figure 5. Evolution of QD-chaotic solution 






Figure 6. The spatial structure of QD-chaotic solution 





Figure 7. The development of temporal chaotic regime of 1D Euclidian quantum N-model at point





Figure 8. The development of temporal chaotic regime of 1D Euclidian quantum N-model at point x = 1, 


Figure 9. Normalized local auto-correlation function





In paper [7] the mechanism of the onset of chaos and its relationship to the characteristics of the spiral attractors are demonstrated for inhomogeneous media that can be modeled by the Ginzburg-Landau Equation (4.14). Numerical data are compared with experimental results (in Figure 11).

However, as pointed out above (see Remarks 1.1-1.4) such numerical simulation in fact gives numerical data for stochastic model
Figure 10. Normalized local auto-correlation function





Figure 11. Normalized local auto-correlation function 

5. The Order of the Phase Transition from a Spatially Uniform State to a Turbulent State at Instant
In order to obtain the character of the phase transition (first-order or second-order on parameters


By differentiation Equation (5.1) one obtain

From Equation (5.2) one obtain

Let us consider now 1D Euclidian quantum N-model given by Equations (4.9)-(4.10). From corresponding transcendental master Equation (4.13) by differentiation Equation (4.13) with respect to variable 

From Equation (5.4) for a sufficiently small 

From master Equation (4.13) one obtain by differentiation Equation (4.13) with respect to variable 

From Equation (5.6) for a sufficiently small 

Therefore from Equation (5.3), (5.5) and (5.7) one obtain

In the 

and where

From Equation (5.9) follows that


From Equations (5.10)-(5.11) follows second order discontinuity of the quantity 


6. Chaotic Regime Generated by Periodical Multi-Modes External Perturbation
Assume now that external periodical force 
Figure 12. Evolution of QD-chaotic solution 










Corresponding transcendental master equation are (Figure 13)

Let us consider the examples of QD-chaotic solutions with a periodical force (Figure 14):
Figure 13. The spatial structure of QD-chaotic solution 









Figure 14. The spatial structure of QD-chaotic solution 










7. Conclusion
A non-perturbative analytical approach to the studying of problem of quantum chaos in dynamical systems with infinite number of degrees of freedom is proposed and developed successfully. It is shown that the additive thermal noise destabilizes dramatically the ground state of the system thus causing it to make a direct transition from a spatially uniform to a turbulent state.
Acknowledgements
A reviewer provided important clarifications.
Cite this paper
Jaykov Foukzon,, (2015) New Scenario for Transition to Slow 3-D Turbulence. Journal of Applied Mathematics and Physics, 03, 371-389. doi: 10.4236/jamp.2015.33048
References
- Nikolaevskii, V.N. (1989) Recent Advances in Engineering Science. In: Kohand, S.L. and Speciale, C.G., Eds., Lecture Notes in Engineering, No. 39, Springer-Verlag, Berlin, 210.
- Tribelsky, M.I. and Tsuboi, K. (1996) Newscenario to Transition to Slow Turbulence. Physical Review Letters, 76, 1631.
http://dx.doi.org/10.1103/PhysRevLett.76.1631 - Tribel’skii, M.I. (1997) Short-Wavelength Instability and Transition to Chaos in Distributed Systems with Additional Symmetry. Physics-Uspekhi, 40, 159-180.
- Toral, R., Xiong, G.X., Gunton, J.D. and Xi, H.W. (2003) Wavelet Description of the Nikolaevskii Model. Journal of Physics A: Mathematical and General, 36, 1323.
http://dx.doi.org/10.1088/0305-4470/36/5/310 - Xi, H.W., Toral, R., Gunton, D. and Tribelsky, M.I. (2003) Extensive Chaos in the Nikolaevskii Model. Physical Review E, 61, R17.
http://dx.doi.org/10.1103/PhysRevE.62.R17 - Tanaka, D. (2007) Amplitude Equations of Nikolaevskii Turbulence. RIMS Kokyuroku Bessatsu, B3, 121-129.
- Fujisaka, H. (2003) Amplitude Equation of Higher-Dimensional Nikolaevskii Turbulence. Progress of Theoretical Physics, 109, 911-918.
http://dx.doi.org/10.1143/PTP.109.911 - Tanaka, D. (2005) Bifurcation Scenario to Nikolaevskii Turbulence in Small Systems. Journal of the Physical Society of Japan, 74, 2223-2225.
- Anishchenko, V.S., Vadivasova, T.E., Okrokvertskhov, G.A. and Strelkova, G.I. (2005) Statistical Properties of Dynamical Chaos. Physics-Uspekhi, 48, 151.
http://dx.doi.org/10.1070/PU2005v048n02ABEH002070 - Tsinober, A. (2014) The Essence of Turbulence as a Physical Phenomenon. 6, 169 p.
http://www.springer.com/gp/book/9789400771796 - Ivancevic, V.G. (2007) High-Dimensional Chaotic and Attractor Systems: A Comprehensive Introduction. XV, 697 p.
http://www.springer.com/gp/book/9781402054556 - Herbst, B.M. and Ablowitz, M.J. (1989) Numerically Induced Chaos in the Nonlinear Schrodinger Equation. Physical Review Letters, 62, 2065.
http://dx.doi.org/10.1103/PhysRevLett.62.2065 - Ablowitz, M.J. and Herbst, B.M. (1990) On Homoclinic Structure and Numerically Induced Chaos for the Nonlinear Schrodinger Equation. SIAM Journal on Applied Mathematics, 50, 339-351.
http://dx.doi.org/10.1137/0150021 - Li, Y. and Wiggins, S. (1997) Homoclinic Orbits and Chaos in Discretized Perturbed NLS Systems: Part II. Symbolic Dynamics. Journal of Nonlinear Science, 7, 315-370.
http://dx.doi.org/10.1007/BF02678141 - Blank, M.L. (1997) Discreteness and Continuity in Problems of Chaotic Dynamics. Translations of Mathematical Monographs. 161 p.
http://www.ams.org/bookstore-getitem/item=MMONO-161 - Fadnavis, S. (1998) Some Numerical Experiments on Round-Off Error Growth in Finite Precision Numerical Computation.
http://arxiv.org/abs/physics/9807003v1 - Fiedler, B., Ed. (2002) Handbook of Dynamical Systems. Volume 2, 1086.
http://www.sciencedirect.com/science/handbooks/1874575X/2 - Gold, B. and Rader, C.M. (1966) Effects of Quantization Noise in Digital Filters. Proceedings of Joint Computer Conference, 26-28 April 1966, 1-8.
http://users.ece.utexas.edu/~adnan/comm/sqnr-early-paper-66.pdf - Bennett, W.R. (1948) Spectra of Quantized Signals. Bell System Technical Journal, 27, 446-472.
http://dx.doi.org/10.1002/j.1538-7305.1948.tb01340.x - Vladimirov, I.G. and Diamond, P. (2002) A Uniform White-Noise Model for Fixed-Point Roundoff Errors in Digital Systems. Automation and Remote Control, 63, 753-765.
http://dx.doi.org/10.1023/A:1015493820232 - Moller, M., Lange, W., Mitschke, F., Abraham, N.B. and Hubner, U. (1989) Errors from Digitizing and Noise in Estimating Attractor Dimensions. Physics Letters A, 138, 176-182.
- Widrow, B. and Kollar, I. (2008) Quantization Noise: Round off Error in Digital Computation, Signal Processing, Control, and Communications. Cambridge University Press, Cambridge.
- Foukzon, J. (2005) Advanced Numerical-Analytical Methods for Path Integral Calculation and Its Application to Some Famous Problems of 3-D Turbulence Theory. New Scenario for Transition to Slow Turbulence. Preliminary Report. Meeting: 1011, Lincoln, Nebraska, AMS CP1, Session for Contributed Papers.
http://www.ams.org/meetings/sectional/1011-76-5.pdf - Foukzon, J. (2004) New Scenario for Transition to Slow Turbulence. Turbulence Like Quantum Chaos in Three Dimensional Model of Euclidian Quantum Field Theory. Preliminary Report. Meeting: 1000, Albuquerque, New Mexico, SS 9A, Special Session on Mathematical Methods in Turbulence.
http://www.ams.org/meetings/sectional/1000-76-7.pdf - Foukzon, J. (2008) New Scenario for Transition to Slow Turbulence. Turbulence like Quantum Chaos in Three Dimensional Model of Euclidian Quantum Field Theory.
http://arxiv.org/abs/0802.3493 - Foukzon, J. (2014) Large Deviations Principles of Non-Freidlin-Wentzell Type. Communications in Applied Sciences, 2, 230-363.
- Foukzon, J. (2014) Large Deviations Principles of Non-Freidlin-Wentzell Type. 227 p.
http://arxiv.org/abs/0803.2072 - Colombeau, J. (1985) Elementary Introduction to New Generalized Functions Math. Studies 113, North Holland.
- Catuogno, P. and Olivera, C. (2013) Strong Solution of the Stochastic Burgers Equation.
http://arxiv.org/abs/1211.6622v2 - Oberguggenberger, M. and Russo, F. (1998) Nonlinear SPDEs: Colombeau Solutions and Pathwise Limits.
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.40.8866 - Walsh, J.B. Finite Element Methods for Parabolic Stochastic PDE’s. Potential Analysis, 23, 1-43.
http://link.springer.com/article/10.1007/s11118-004-2950-y - Suli, E. (2000) Lecture Notes on Finite Element Methods for Partial Differential Equations. University of Oxford, Oxford.
http://people.maths.ox.ac.uk/suli/fem.pdf - Knabner, P. and Angermann, L. (2003) Numerical Methods for Elliptic and Parabolic Partial Differential Equations.
http://link.springer.com/book/10.1007/b97419 - Dijkgraaf, R., Orlando, D. and Reffert, S. (2010) Relating Field Theories via Stochastic Quantization. Nuclear Physics B, 824, 365-386.
http://dx.doi.org/10.1016/j.nuclphysb.2009.07.018 - Masujima, M. (2009) Path Integral Quantization and Stochastic Quantization. 2nd Edition.
http://www.gettextbooks.com/isbn/9783540665427








































