Journal of Applied Mathematics and Physics
Vol.2 No.8(2014), Article
ID:47818,4
pages
DOI:10.4236/jamp.2014.28088
From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2014; revised 25 June 2014; accepted 2 July 2014
ABSTRACT
Starting from the classical Newton inverse square law of gravitation we arrive at a modified Newtonian gravity in the spirit of the work of Milgrom-Bekenstein pioneering work. This is achieved by injecting the needed quantum mechanical dissection of special relativity into Newton’s law via the modified energy mass relationship which transforms Einstein’s famous formula 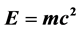 from a smooth four dimensional space to a rugged fractal-like spacetime manifold. The confidence in the present result stems not only from the consistency of the mathematical scheme but also from agreement with the general direction of cosmological measurements and observations.
from a smooth four dimensional space to a rugged fractal-like spacetime manifold. The confidence in the present result stems not only from the consistency of the mathematical scheme but also from agreement with the general direction of cosmological measurements and observations.
Keywords:Milgrom Modified Newtonian Gravity, Bekenstein Gravity Theory, Quantum Entanglement, Dark Energy, Revising Special Relativity, Cantorian Spacetime

1. Introduction
Newton’s well known inverse square law of gravitation is as exceptionally successful as it is simple to write down for two masses 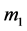 and
and 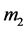 separated by a distance
separated by a distance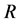 . The force of gravitational attraction
. The force of gravitational attraction 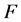 in this case is simply [1] [2]
in this case is simply [1] [2]
![]() (1)
(1)
where ![]() is Newton’s gravitational constant. There has to be something much deeper than classical mechanics in this law because its basic form holds true for electric as well as magnetic charges [1] -[4] . Of course things become immensely complex when we move from the integrable two-body problem to the nonintegrable threebody and more problem [3] . This subject is studied within the modern theory of dynamical systems, deterministic chaos and fractals initiated by Poincaré and Kolmogorov, Arnold and Moser and culminated in the formulation of KAM theorem [3] -[7] . This theory in turn is rooted in many subjects particularly number theory [8] -[10] , transfinite set theory, the continuum hypothesis [9] [11] and the hierarchy of infinites as well as the zero and empty sets hierarchy [12] . Other extremely relevant pure mathematical subjects are the Menger-Urysohn deductive dimensional theories [13] , K-theory, E-infinity theory and Woodin’s ultimate L-theory [9] [10] .
is Newton’s gravitational constant. There has to be something much deeper than classical mechanics in this law because its basic form holds true for electric as well as magnetic charges [1] -[4] . Of course things become immensely complex when we move from the integrable two-body problem to the nonintegrable threebody and more problem [3] . This subject is studied within the modern theory of dynamical systems, deterministic chaos and fractals initiated by Poincaré and Kolmogorov, Arnold and Moser and culminated in the formulation of KAM theorem [3] -[7] . This theory in turn is rooted in many subjects particularly number theory [8] -[10] , transfinite set theory, the continuum hypothesis [9] [11] and the hierarchy of infinites as well as the zero and empty sets hierarchy [12] . Other extremely relevant pure mathematical subjects are the Menger-Urysohn deductive dimensional theories [13] , K-theory, E-infinity theory and Woodin’s ultimate L-theory [9] [10] .
With all these subjects in the back of our mind it is no longer possible to think of Newton’s inverse square law of gravitation as being the final word on the subject, particularly with the benefit of modern measurements and observational anomalies which cast doubt on the universal validity of this law [14] [15] . For instance and as far as pure mathematics is concerned, for the two extreme cases, namely ![]() and
and 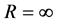 we have
we have 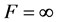 and
and ![]() respectively. Of course we know in principle that infinity and zero are not numbers but deep philosophical concepts. The Indian are normally credited with “inventing” the zero but the Arabs are definitely the ones who communicated the “Zifr”, i.e. the zero to medieval Europe. In fact the word “ziffers”, i.e. numbers come from the Arabic “Zifr” which means zero. Be what it may be, a definite value such as zero does not exist in quantum mechanics because of Heisenberg’s uncertainty principles [1] [2] . Infinity on the other hand is quite vague because there is a hierarchy of countable and incommensurate “uncountable” infinities and each is larger than the other [9] [12] . Since infinity is the result of inverting the zero, then there must be many sets which correspond to things smaller than the zero, namely empty and emptier still, empty sets [12] . Luckily we do not need to worry about all these things in the average normal situations. However when probing extremely small distances near to the Planck length as well as unimaginably large distances taking us near to the borders of the holographic Klein-Penrose hyperbolic compactified projection of our bulk universe [5] [10] , then we must worry about all these subtle deep mathematical concepts related to zero and infinity.
respectively. Of course we know in principle that infinity and zero are not numbers but deep philosophical concepts. The Indian are normally credited with “inventing” the zero but the Arabs are definitely the ones who communicated the “Zifr”, i.e. the zero to medieval Europe. In fact the word “ziffers”, i.e. numbers come from the Arabic “Zifr” which means zero. Be what it may be, a definite value such as zero does not exist in quantum mechanics because of Heisenberg’s uncertainty principles [1] [2] . Infinity on the other hand is quite vague because there is a hierarchy of countable and incommensurate “uncountable” infinities and each is larger than the other [9] [12] . Since infinity is the result of inverting the zero, then there must be many sets which correspond to things smaller than the zero, namely empty and emptier still, empty sets [12] . Luckily we do not need to worry about all these things in the average normal situations. However when probing extremely small distances near to the Planck length as well as unimaginably large distances taking us near to the borders of the holographic Klein-Penrose hyperbolic compactified projection of our bulk universe [5] [10] , then we must worry about all these subtle deep mathematical concepts related to zero and infinity.
In physics quantum gravity [5] [10] as well as dark energy [18] [19] are inextricably connected to these fundamental problems of pure mathematics [3] [8] [9] [12] . In what follows we show a logical way to overcome at least some of these problems and limitations via the magic of Hardy’s quantum entanglement and arrive that way at a modified Newtonian formula which agrees with measurements as far as energy is concerned, i.e. when converting dark matter to dark energy theoretically using Einstein’s equations [1] [18] -[25] .
2. Modified Gravity via Quantum Entanglement
We know from recent intense research that Einstein’s most fundamental and equally elegant formula relating energy to mass and the “constant” speed of light [1]
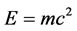 (2)
(2)
when seen under a magnifying “transfinite” microscope of set theory and quantum mechanics, consists of two parts. The first part [18] [19]
![]() (3)
(3)
is the quasi potential energy of the quantum particle. This part of the energy is merely 4.5% of the total energy density in the universe and can be measured in a rather conventional although sophisticated way. The second part [10] [19]
![]() (4)
(4)
is the quasi kinetic energy of the supposedly energy-less quantum wave which guides the particle as it propagates through quantum space. Thus 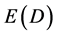 amounts to 95.5% of the total energy density. The delightful final result, which stresses the consistency and correctness of this picture, is that the sum of both energies adds to that of Einstein’s beauty, namely [10] [18] [19]
amounts to 95.5% of the total energy density. The delightful final result, which stresses the consistency and correctness of this picture, is that the sum of both energies adds to that of Einstein’s beauty, namely [10] [18] [19]
![]() (5)
(5)
as should be. The vital difference between 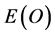 and
and 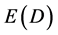 is that in contrast to
is that in contrast to 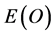 we cannot measure
we cannot measure 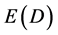 using any of the presently known methods because of a fundamental property of orthodox quantum mechanics called quantum wave collapse on measurement [10] [18] [19] . Now we apply the above to Newton’s classical gravitational law. We start by expressing the mass
using any of the presently known methods because of a fundamental property of orthodox quantum mechanics called quantum wave collapse on measurement [10] [18] [19] . Now we apply the above to Newton’s classical gravitational law. We start by expressing the mass  in terms of the only energy we can measure, namely
in terms of the only energy we can measure, namely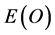 . Consequently we can write for the force due to ordinary matter corresponding the
. Consequently we can write for the force due to ordinary matter corresponding the 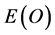 ordinary energy that
ordinary energy that
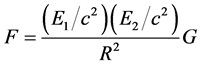 (6)
(6)
and find the measurable F to be
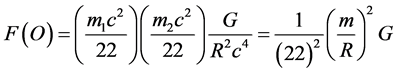 (7)
(7)
where the factor 22 could be interpreted in two different ways [18] [19] . First it could be seen as the compactified dimension of Nambu-Veneziano 26 bosonic string theory spacetime dimensions after subtracting the 4 large dimensions of Einstein’s spacetime. The second interpretation is to see the factor 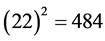 as being the remaining massless gauge bosons of E8E8 superstring theory after subtracting the 12 massless bosons of the standard model [18] [19] . That means [18] [19]
as being the remaining massless gauge bosons of E8E8 superstring theory after subtracting the 12 massless bosons of the standard model [18] [19] . That means [18] [19]
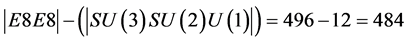 (8)
(8)
exactly as it should be [18] [19] . However this is by no means the end of the story because we have still 20 per cent dark matter included in the 95.5% dark energy. This complicates the real situation considerably and will be discussed in subsequent research.
3. Conclusion
In full agreement with what has repeatedly been expressed by leading mainstream scientists as well as mavericks [16] [17] who do not shrug from contradicting conventional wisdom when faced with undeniable imperical data, firm measurements and observations and that applies not only to Einstein’s general theory but even and maybe more so, to the special theory of relativity breaks down in an organized very specific way at Witten’s T-duality extremities [1] , i.e. at the imaginable small distances as well as the unimaginable large distances [18] [19] . On average we find an energy-mass relationship which consists of two parts. The part which we can measure happened to be given by![]() . The other part, dubbed dark energy is
. The other part, dubbed dark energy is ![]() and cannot be measured in any direct way known at present. However its reality is clearly inferred from the accelerated rather than decelerating cosmic expansion confirmed by all modern accurate cosmological measurements and analysis [10] [18] [19] . Needless to say, the situation is quite complex because part of the
and cannot be measured in any direct way known at present. However its reality is clearly inferred from the accelerated rather than decelerating cosmic expansion confirmed by all modern accurate cosmological measurements and analysis [10] [18] [19] . Needless to say, the situation is quite complex because part of the 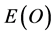 is in the form of ordinary matter and that 20 percent of the (21/22) percent is conjectured to be dark matter with attractive force leading to astrophysical contradictions to observations. We should remark that in itself Newtonian attraction can calculate almost everything except dark matter and dark energy. However Newton’s law really explains nothing and does not make it one bit clearer why matter is self attracting. In that respect Einstein’s theory fares better but does not capture the complete picture. Only when we take on board fractal-Cantorian geometry with its zero measure thin fractals and positive measure fat fractals implying quantum entanglement do we come to an almost complete understanding at least as far as dark energy and quantum gravity is concerned at present [10] [18] [19] . In conclusion we should draw attention to the deep relation between earlier publications by Czajko and El Naschie [20] -[25] and the present work as far as dark matter and deriving Newton’s gravitational constant from first principles is concerned. The connection to Witten’s T-duality [26] is equally important for understanding our present viewpoint.
is in the form of ordinary matter and that 20 percent of the (21/22) percent is conjectured to be dark matter with attractive force leading to astrophysical contradictions to observations. We should remark that in itself Newtonian attraction can calculate almost everything except dark matter and dark energy. However Newton’s law really explains nothing and does not make it one bit clearer why matter is self attracting. In that respect Einstein’s theory fares better but does not capture the complete picture. Only when we take on board fractal-Cantorian geometry with its zero measure thin fractals and positive measure fat fractals implying quantum entanglement do we come to an almost complete understanding at least as far as dark energy and quantum gravity is concerned at present [10] [18] [19] . In conclusion we should draw attention to the deep relation between earlier publications by Czajko and El Naschie [20] -[25] and the present work as far as dark matter and deriving Newton’s gravitational constant from first principles is concerned. The connection to Witten’s T-duality [26] is equally important for understanding our present viewpoint.
References
- Penrose, R. (2004) The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape, London.
- Hawking, S. (2001) The Universe in a Nutshell. Bantam Press, London.
- Kiacu, F. and Holmes, P. (1996) Celestial Encounters—The Origin of Chaos and Stability. Princeton University Press, Princeton.
- El Naschie, M.S. (1990) Stress, Stability and Chaos in Structural Engineering—An Energy Approach. McGraw Hill, London.
- El Naschie, M.S. (2006) Elementary Prerequisites for E-Infinity (Recommended Background Readings in Nonlinear Dynamics, Geometry and Topology). Chaos, Solitons & Fractals, 30, 579-605. http://dx.doi.org/10.1016/j.chaos.2006.03.030
- Arnold, V.I., Ed. (1988) Dynamical Systems III. Springer, New York. http://dx.doi.org/10.1007/978-3-662-02535-2
- Guckenheimer, J. and Holmes, P. (1983) Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-1140-2
- Hardy, G.H. and Wright, E.M. (2008) An Introduction to the Theory of Numbers. 6th Edition, Oxford University Press, Oxford.
- Elwes, R. and Ultimate, L. (2011) Ultimate Logic. New Scientist, 211, 30-33. http://dx.doi.org/10.1016/S0262-4079(11)61838-1
- Marek-Crnjac, L., El Naschie, M.S. and He, J.-H. (2013) Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology. International Journal of Modern Nonlinear Theory and Application, 2, 78-88.
- El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- He, J.-H., et al. (2011) The Importance of the Empty Set and Noncommutative Geometry in Underpinning the Foundations of Quantum Physics. Nonlinear Science Letters B, 1, 14-23.
- Ho, M.-W. (2014) Golden Geometry of E-Infinity Fractal Spacetime. The Story of Phi, Part 5, Science of the Organism, Institute of Science in Society. www.i-sis.org.uk
- Milgrom, M. (1983) A Modification of the Newtonian Dynamics—Implications for Galaxies. Astrophysical Journal, 270, 371-389. http://dx.doi.org/10.1086/161131
- Bekenstein, J. (2006) The Modified Newtonian Dynamics—MOND—and Its Implication for New Physics. Contemporary Physics, 47, 387. http://dx.doi.org/10.1080/00107510701244055
- Zwicky, F. (1934) On the Principle of Flexibility of Scientific Truth. Philosophy of Science, 1, 353-359. http://dx.doi.org/10.1086/286334
- Zwicky, F. and Zwicky, M. (1971) Catalogue of Selected Compact Galaxies and Post-Eruptive Galaxies. Guemligen, Switzerland.
- El Naschie, M.S. (2014) Cosmic Dark Energy from t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91. http://dx.doi.org/10.4236/jqis.2014.42008
- El Naschie, M.S. (2014) Cosserat-Cartan Modification of Einstein-Riemann Relativity and Cosmic Dark Energy Density. American Journal of Modern Physics, 3, 82-87.
- El Naschie, M.S. (2006) Is Einstein’s General Field Equation More Fundamental than Quantum Field Theory and Particle Physics? Chaos, Solitons & Fractals, 30, 525-531. http://dx.doi.org/10.1016/j.chaos.2005.04.123
- El Naschie, M.S. (2006) Is Gravity Less Fundamental than Elementary Particles Theory? Critical Remarks on Holography and E-Infinity Theory. Chaos, Solitons & Fractals, 29, 803-807. http://dx.doi.org/10.1016/j.chaos.2006.01.012
- El Naschie, M.S. (2008) Derivation of Newton’s Gravitational Fine Structure Constant from the Spectrum of Heterotic Superstring Theory. Chaos, Solitons & Fractals, 35, 303-307. http://dx.doi.org/10.1016/j.chaos.2007.07.025
- Czajko, J. (2005) On the Universe’s Missing Mass. Chaos, Solitons & Fractals, 23, 11-22. http://dx.doi.org/10.1016/j.chaos.2004.03.032
- El Naschie, M.S. (2008) Exact Non-Perturbative Derivation of Gravity Fine Structure Constant, the Mass of the Higgs and Elementary Black Holes. Chaos, Solitons & Fractals, 37, 346-359. http://dx.doi.org/10.1016/j.chaos.2007.10.021
- El Naschie, M.S. (2005) Gödel Universe, Dualities and High Energy Particles in E-Infinity. Chaos, Solitons & Fractals, 25, 759-764. http://dx.doi.org/10.1016/j.chaos.2004.12.010
- El Naschie, M.S. (2005) A Few Hints and Some Theorems about Witten’s M-Theory and T-Duality. Chaos, Solitons & Fractals, 25, 545-548. http://dx.doi.org/10.1016/j.chaos.2005.01.009

