Open Journal of Philosophy
Vol.04 No.01(2014), Article ID:43299,4 pages
10.4236/ojpp.2014.41008
Model Theories of Set Theories and Type Theory
Robert Murray Jones
University of Duesseldorf, Duesseldorf, Germany
Email: jones@uni-duesseldorf.de
Copyright © 2014 Robert Murray Jones. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Robert Murray Jones. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
This paper is divided into three parts. In the first part, we review the historical background of a system of logic devised by Henry S. Leonard to allow for reasoning using existence as a predicate. In the second part, we consider various directions in which his logic could be further developed, syntactically, semantically, and as an adjunct to quantifier elimination and set theory. In the third and final part, we develop proofs of some underlying results of his logic, using modern notation but retaining his axioms and rules of inference.
Keywords: Models; Set Theory; Quantified Modal Logic; Existence Predicate
Introduction
Mathematicians frequently use names without knowing whe- ther a corresponding ostensible object exists. In (Jones, 2013: pp. 3-4) we discussed the example of the term Monster Group. In this paper, we extend historical work of Henry S. Leonard (Leonard, 1969), and its results, with methodologies that were unavailable when those results were first written. In (Jones, 2013: pp. 3-4) we outlined, in summary form, several lines of development that now are open to investigation using currently available advances in logic. We confine ourselves here to those further developments that can be described within first-order model theory.
Historical Background
Leonard (Leonard, 1969) proposed an influential definition of singular existence as a predicate:
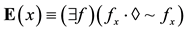
His definition was embedded in a system of logic that provided for deductive reasoning using existence as a predicate. His definition and his system of logic were proposed to use methods of logic, such as quantified modal logic, that were underdeveloped at the time he wrote. At that time, the leading conjecture in quantified modal logic was the Barcan Formula: . This formula had been proposed by Ruth C. Barcan in her papers Barc1, (Barcan, 1946b), and (Barcan, 1947). Almost no further contributions to the development of quantified modal logic were then available, either as commentary, speculation, or conjecture. Leonard was thus remarkably aggressive in using quantified modal logic in his definition of singular existence as a predicate. He presumed the availability of a tool of logic that only later was given an adequate semantics and syntax.
. This formula had been proposed by Ruth C. Barcan in her papers Barc1, (Barcan, 1946b), and (Barcan, 1947). Almost no further contributions to the development of quantified modal logic were then available, either as commentary, speculation, or conjecture. Leonard was thus remarkably aggressive in using quantified modal logic in his definition of singular existence as a predicate. He presumed the availability of a tool of logic that only later was given an adequate semantics and syntax.
Received October 7th, 2013; revised November 7th, 2013; accepted November 17th, 2013
Although little of the methodology that Leonard presupposed was available then, his publication led to our (Jones, 1964) and to the beginning of Free Logic in (Lambert, 1967). After his publication of his system of logic for singular existence as a predicate in Leonard (Leonard, 1969), there was an explosion of results concerning quantified modal logic. The author’s review (Jones, 2013) of the recent book by Goldblatt (Goldblatt, 2011) mentions Leonard’s work and the bibliography of the book offers a set of 119 references to modern work that is pertinent, directly or indirectly, to quantified modal logic.
Goals of This Contribution
We describe a first-order model theory for a logic of existence. Why, one might ask, should one choose first-order logic as an environment in which to develop a model theory for Leonard’s existence logic? Indeed, his definition of existence as a predicate in Section 1.1 seems to directly demand, with its quantified predicate variable, a second-order theory. A first- order model theory of Leonard’s existence logic is not only possible, but confers significant mathematical advantages. We adopt the notation:
 for our proposed logic. In contrast, results in second-order arithmetic, like (Buchi, 1962), require extraordinary reasoning methods such as those discussed in (Baldwin, 1985) and (Gurevich, 1985).
for our proposed logic. In contrast, results in second-order arithmetic, like (Buchi, 1962), require extraordinary reasoning methods such as those discussed in (Baldwin, 1985) and (Gurevich, 1985).
Syntax of First-Order Logic for an Existence Predicate
We introduce the predicate constant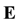 . The assertion
. The assertion
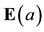 is to be interpreted as: a exists. Leonard’s syntactical specification of first-order logic requires the following change to one of the standard axioms of quantification.
is to be interpreted as: a exists. Leonard’s syntactical specification of first-order logic requires the following change to one of the standard axioms of quantification.
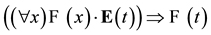 (1)
(1)
This axiom is sometimes called
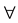 -elimination, (Kleene, 1950: 23).
-elimination, (Kleene, 1950: 23).
Where t is free for x in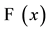 . We follow notational conventions for the predicate calculus from Kleene (Kleene, 1950: Chapter VII).
. We follow notational conventions for the predicate calculus from Kleene (Kleene, 1950: Chapter VII).
We assume in this paper that the logic
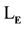 is augmented with a theory of the form
is augmented with a theory of the form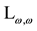 . We hope later to extend these results to theories of the form
. We hope later to extend these results to theories of the form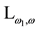 . We wish also to accommodate Quine’s view (Quine, 1948) that everything exists. To this end, we incorporate additional axioms for the existence predicate:
. We wish also to accommodate Quine’s view (Quine, 1948) that everything exists. To this end, we incorporate additional axioms for the existence predicate:
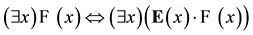 (2)
(2)
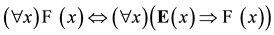 (3)
(3)
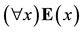 (4)
(4)
We do not attempt to formulate a minimal set of independent axioms. One of the above principles of Quine would suffice. We mention all three for the sake of clarity and completeness of exposition.
Semantics of First-Order Model Theory for an Existence Predicate
We describe model theory for first-order predicate logic with equality and an existence predicate.
We adopt Lindström’s definition of first-order logic from (Lindstrom, 1969) and follow the discussion of it in Chang and Keisler (Chang, 1990: Section 2.5). Lindström showed that first-order logic can be characterized as the strongest predicate logic that is compact and in which the Downward Löwenheim Skolem Theorem holds.
Compactness of
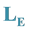
We prove the compactness of
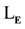 by adapting the proof of compactness in Chang and Keisler (Chang, 1990: Section 2.5).
by adapting the proof of compactness in Chang and Keisler (Chang, 1990: Section 2.5).
Theorem 1 (Compact) The first-order model theory of
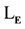 is compact.
is compact.
Proof We note the changes to the proof of compactness (Chang, 1990: Theorem 1.3.22, p. 67). There are preliminary results concerning the model theory of sentential logic in Chang and Keisler (Chang, 1990: Chapter 1). The sentential logic that is assumed there is unchanged in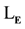 . Those preliminary results are therefore also available here. The key step in the proof shows the existence of witnesses for an existentially quantified statement (Chang, 1990: Lemma 2.1.1, p. 62). This result, which depends upon set theory, would be available in
. Those preliminary results are therefore also available here. The key step in the proof shows the existence of witnesses for an existentially quantified statement (Chang, 1990: Lemma 2.1.1, p. 62). This result, which depends upon set theory, would be available in
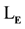 if appropriate axioms of a reduct of set theory, for example Zermelo-Fraenkel Set Theory with the Axiom of Choice, ZFC, are added to it. This step in the proof requires that a new set of constant symbols
if appropriate axioms of a reduct of set theory, for example Zermelo-Fraenkel Set Theory with the Axiom of Choice, ZFC, are added to it. This step in the proof requires that a new set of constant symbols
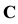 be added to the language. It is important to note that, in
be added to the language. It is important to note that, in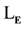 , these constant symbols must be chosen to be among those that refer to an element of the model.
, these constant symbols must be chosen to be among those that refer to an element of the model.
The remainder of the proofs that lead up to the final result, Theorem 1.3.22 (Compactness Theorem), (Chang, 1990: p. 67) remain identically the same as those given there. They can therefore be taken over unchanged into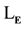 .
.
We next prove that
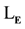 satisfies the Downward Löwenheim Skolem Theorem.
satisfies the Downward Löwenheim Skolem Theorem.
Theorem 2 (Downward Lowenheim Skolem) The first- order model theory of
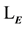 satisfies the Downward Löwenheim Skolem Theorem.
satisfies the Downward Löwenheim Skolem Theorem.
Proof We note again the changes to the proof of the corresponding theorem in Chang and Keisler (Chang, 1990: Corollary 2.1.4, p. 66). The selection of a set
 of constants plays a central role in the proof. Again, as above, for
of constants plays a central role in the proof. Again, as above, for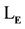 , these constant symbols must be chosen to be among those that refer to an element of the model. As in the proof of Theorem 1, the remainder of the proof remains identically the same as that given in (Chang, 1990: p. 66). It can therefore be taken over unchanged into
, these constant symbols must be chosen to be among those that refer to an element of the model. As in the proof of Theorem 1, the remainder of the proof remains identically the same as that given in (Chang, 1990: p. 66). It can therefore be taken over unchanged into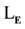 .
.
The Definition of Truth in the Formal Language of a Model
A model of a language consists of domain of discourse in a structure, and an assignment function that assigns elements of the structure to elements of the language. We assume standard definitions of truth and satisfaction as these terms are used in model theory. We indicate how these definitions may be amen- ded to accommodate an existence predicate. The definition of truth in a model begins with a definition of truth for atomic as- sertions, and proceeds by truth tables to the definition of truth for compound assertions.
The assignment function assigns elements of the domain of discourse of the model to argument constants of the language. The assignment function also assigns subsets of the domain of discourse of the model to unary predicate constants of the language. If F is a unary predicate constant and a is an argument constant, then
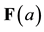
asserts that the element a of the universe of discourse of the model satisfies the predicate F. This assertion is true if the assignment function assigns to a an element of the subset of the universe of discourse of the model that it assigns to F. This assertion is false if it is not true.
In conventional model theory, this assignment function is complete. Each constant of the language is assigned an element of the domain of discourse. Perhaps the most fundamental way in which model theory for first-order logic with an existence predicate differs from conventional model theory is that this assignment function is partial for argument constants.
Because the assignment function is a partial function for argument constants, it is possible that the assignment function does not assign an element of the domain of discourse of the model to a in the above example. In the latter case the truth condition for that assertion is not met, and the assertion is accordingly false. The following assertion is then, by the truth table for the negation truth-function, true:
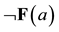 ,
,
and indeed the assertion that the ostensible element of the universe of discourse of the model does not exist is also true:
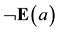 .
.
The possibility of a true assertion of the falsity of the asserted existence of an ostensible element of the model is an objective of first-order model theory with an existence predicate. Such an assertion, it should be noted, is compatible with Quine’s three conditions for the universality of the existence predicate listed in Section 2.
Elimination of Quantifiers
The proofs of results concerning compactness and the Down- ward Löwenheim Skolem Theorem require the method of proof by elimination of quantifiers. The history of the method of proof by elimination of quantifiers, and its development in the writings of Cegielski, Herbrand, Presburger, and Skolem, are discussed in (Smory?ki, 1991: p. 402).
Presburger Arithmetic
We wish to discuss one of these authors in detail as an example of the adaptation of their proofs, using quantifier elimination, in a way compatible with our first-order logic of existence. We have chosen Presburger (Presburger, 1929) for this example. Presburger Arithmetic is well suited to such an examination, for several reasons. Presburger’s paper was a classical discovery in metamathematics that is complementary to Gödel’s First Theorem (Godel, 1931). Gödel’s and Presburger’s arithmetics differ simply in that the former includes multiplication by a variable, while the latter allows only multiplication by a constant. Yet, they are drastically different. Gödel’s arithmetic is incomplete, while Presburger’s arithmetic is complete and has a decision procedure.
For the sake of accuracy of reference, we prefer to use the page numbers of the German language original text of Presbur- ger’s conference publication and of the addendum to it that ap- peared on a later page in the same volume of conference pro- ceedings.
Pages 92-94
Here Presburger decides upon his choice of sentential connectives, using the system of Łukasiewicz. This approach would allow all formulas to be written without parentheses, but he allows parentheses as well. He introduces here the two constants 0 and 1. This first-order logic of existence would require no change to the sentential connectives because the sentential part of conventional logic is retained unchanged. The constants 0 and 1 would, however, require the additional axioms:
and

He also introduces here the existential quantifier. He explains how multiplication by a constant, but not by a variable, is pos- sible in his arithmetic. This is so because multiplication by a constant is equivalent to a finite series of additions.
Pages 95-97
Here Presburger defines the forms of ground statements, discusses disjunctive normal for compound statements, and the method of elimination of quantifiers, with a footnote attributing this method to Skolem and Langford. On page 97 he formulates his main lemma, which claims that assertions of his language can be brought into disjunctive normal form with elimination of quantifiers.
Page 98
Here, Presburger defines six classes of assertions which he will subsequently use to prove his main lemma. His proof is by cases in which each of the six classes of assertions is separately treated.
Pages 99-101
He examines the proof by cases with quantifier elimination and concludes the proof of the main lemma.
Addendum, Page 395
In this section we consider the system of arithmetic that Presburger defines in an addendum in the same volume of the conference proceedings in which his paper appeared. It is a system that is also complete, but is more difficult to prove complete than the famous system, with integers and (Z,+,0,1), which he considers in the main body of the article. It includes the natural numbers and (N,+,−,0,1,<).
A modern treatment of the latter arithmetic, with a proof of completeness, is in (Monk, 1976, page 237). Monk calls this system of arithmetic
In Section 4.3, Presburger chooses sentential connectives that are notationally different from those we adopt, but which require no change to his proof. He also specifies constants that must be chosen to refer to elements of the model. In section 4.4 Presburger introduces disjunctive normal form for ground state- ments. This step in his proof is the source of the notoriously severe computational intractability of his decision procedure, having a doubly exponential time bound, for arithmetic with (Z,+,0,1). Fischer and Rabin (Fischer, 1974) showed that Presburger’s decision procedure is at least doubly exponential. This result precludes the practical usefulness of this decision procedure, but it has no effect upon the matter we consider, the validity of his proof of completeness.
Requirements of the Logic of the Proof
In this Section we examine the adaptations of Presburger’s proof that are required by the logic of the existence predicate, due to Leonard, that we are here proposing. We now can make use of the modifications to Presburger’s paper noted above to adapt his proof to our logic,
Proof
In this central step of the proof, Section 4.5, Presburger defines six cases for each of which he intends to perform quantifier elimination. There is a common thread that runs through the cases of quantifier elimination in the pages of this Section, 4.6. It is the use of constants to replace existential quantifiers. These constants must, in the present system


The proofs of Theorem 1 and Theorem 2 called for quite modest changes to the original proofs; the latter do not impinge upon those aspects of


Set Theory in the Model Theory of Predicate Logic
In the previous sections, we have established that this model theory with its modified predicate logic has the standard characteristics that one would expect of a predicate logic for axiom systems of mathematics. In this section 5, we apply this system of predicate logic to a weak version of ZF set theory. We refer to the axioms for ZF given in Jech (Jech, 2006).
Conclusion
We are quite far from having fully exploited the potential of Leonard’s definition of an existence predicate. The present pa- per gives a limited account of that potential within first-order logic. The system that we have presented here does not suffice for the derivations that we made in our (Jones, 1964). There we assumed the full type theory of Principia Mathematica (White- head, 1910). Many, if not most, of the results proved there could have been obtained with a simple version of type theory. We hope to explore this possibility in a future publication. We mentioned several directions which a further development of the consequences of Leonard’s definition of an existence predicate might take in (Jones, 2013: pp. 3-4).
Acknowledgements
We are indebted to Henry S. Leonard for his paper (Leonard, 1969). We also are indebted to him for his formulation, in conversation, of Axiom (3) of Section 2. He suggested it as a formal account of Quine’s view that the singular existence predicate is universal. We are indebted to former students of Henry S. Leonard, including Joanne Eicher (University of Minnesota, Twin Cities) and Rolf George (University of Waterloo, Ontario), for their recollections of their study under him and for their help in reconstructing his ideas and intentions.
References
- Baldwin, J. (1985). Definable second-order quantifiers. In J. Barwise, & S. Feferman (Eds.), Model-theoretic logics (pp. 445-477). New York: Springer-Verlag.
- Barcan, R. C. (1946). A functional calculus of first order based on strict implication. Journal of Symbolic Logic, 11, 1-16. http://dx.doi.org/10.2307/2269159
- Barcan, R. C. (1946). The deduction theorem in a functional calculus of first order based on strict implication. Journal of Symbolic Logic, 11, 115-118. http://dx.doi.org/10.2307/2268309
- Barcan, R. C. (1947). The identity of individuals in a strict functional calculus of second order. Journal of Symbolic Logic, 12, 12-15. http://dx.doi.org/10.2307/2267171
- Büchi, J. R. (1962). On a decision method in restricted second order arithmetic. In E. Nagel, P. Suppes, & A. Tarski (Eds.), Logic, metho- dology and philosophy of science (pp. 1-11). Stanford: Stanford Uni- versity Press.
- Chang, C. C., & Keisler, H. J. (1990). Model theory (3rd ed.). Amster- dam: Elsevier.
- Fischer, M. J., & Michael, O. R. (1974). Super-exponential complexity of Presburger arithmetic. In R. M. Karp (Ed.), Complexity of com- putation (pp. 27-41). Providence, RI: American Mathematical Soci- ety.
- Goldblatt, R. (2011). Quantifiers, propositions and identity: Admissible semantics for quantified modal and substructural logics. Cambridge: Cambridge University Press. http://dx.doi.org/10.1017/CBO9780511862359
- Gödel, K. (1931). Über formal unentscheidbare Sätze der principia ma- thematica und verwandter Systeme, I. Monatshefte für Mathematik und Physik, 38, 173-198. http://dx.doi.org/10.1007/BF01700692
- Gurevich, Y. (1985). Monadic second-order theories. In J. Barwise, & S. Feferman (Eds.), Model-theoretic logics (pp. 479-506). New York: Springer-Verlag.
- Jech, T. (2006). Set theory: The third millenium edition (3rd ed.). Berlin: Springer-Verlag.
- Jones, R. M. (1962). A note on obversion. Mind, 284, 541-542. http://dx.doi.org/10.1093/mind/LXXI.284.541
- Jones, R. M. (1964). Formal results in the logic of existence. Philoso- phical Studies, 15, 7-10. http://dx.doi.org/10.1007/BF00428091
- Jones, R. M. (2013) Review of Robert Goldblatt. Philosophia mathe- matica, 21, 115-123.
- Kleene, S. C. (1950). Introduction to metamathematics. New York: D. van Nostrand.
- Lambert, K. (1967). Free logic and the concept of existence. Notre Dame Journal of Formal Logic, 8, 133-144. http://dx.doi.org/10.1305/ndjfl/1093956251
- Leonard, H. S. (1969). The logic of existence. Philosophical Studies, 7, 49-64. http://dx.doi.org/10.1007/BF02221764
- Lindström, P. (1969). On extensions of elementary logic. Theoria, 35, 1-11. http://dx.doi.org/10.1111/j.1755-2567.1969.tb00356.x
- Monk, J. D. (1976). Mathematical logic. New York: Springer-Verlag. http://dx.doi.org/10.1007/978-1-4684-9452-5
- Presburger, M. (1929). Über die Vollständigkeit eines gewissen systems der Arithmetik ganzer Zahlen, in welchem die addition als einzige operation hervortritt in Comptes Rendus du I congrès de Math? maticiens des Pays Slaves, Warszawa, 92-101, Addendum, 395.
- Quine, W. Van O. (1948). On what there is. Review of Metaphysics, 2, 21-38.
- Smory?ski, C. (1991). Logical number theory I: An introduction. Berlin: Springer-Verlag. http://dx.doi.org/10.1007/978-3-642-75462-3
- Whitehead, A. N., & Bertrand, R. (1910). Principia mathematica. Cam- bridge: Cambridge University Press.
- Appendices
- A. Full Proofs
- We here provide details of some proofs that we sketched pre- viously. Some readers have requested further elaboration and explicitness in the proofs. Leonard’s definition of singular ex- istence is quoted in Section 1.1. It appears there in a notation that is close to that which he used to write it. In the proofs that follow we modernize his notation, used in Leonard (Leonard, 1969) and in our (Jones, 1964). Leonard’s definition of singular existence as a predicate, written in modern notation, is D1 in Appendix B.
- Inference 1 (P1).
- 1.
>http://html.scirp.org/file/8-1650292x40.png" class="200" />
- 2.
>http://html.scirp.org/file/8-1650292x41.png" class="200" />
- 3.
>http://html.scirp.org/file/8-1650292x42.png" class="200" />
- 4.
>http://html.scirp.org/file/8-1650292x43.png" class="200" />
- 5.
>http://html.scirp.org/file/8-1650292x44.png" class="200" />
- (Line 1 is a premise of the proof. It is Nc of Appendix B. Line 2 follows from line 1, using Ob1 outside of, and Ob2 within, a modal context. The remaining lines follow from previous lines by propositional logic.)
- Inference 2 (P2).
- 1.
>http://html.scirp.org/file/8-1650292x45.png" class="200" />
- 2.
>http://html.scirp.org/file/8-1650292x46.png" class="200" />
- (Line 1 follows by substitution from L5 of Appendix B. Line 2 follows from line 1 and P1 above.)
- Inference 3 (P3).
- 1.
>http://html.scirp.org/file/8-1650292x47.png" class="200" />
- 2.
>http://html.scirp.org/file/8-1650292x48.png" class="200" />
- 3.
>http://html.scirp.org/file/8-1650292x49.png" class="200" />
- 4.
>http://html.scirp.org/file/8-1650292x50.png" class="200" />
- 5.
>http://html.scirp.org/file/8-1650292x51.png" class="200" />
- 6.
>http://html.scirp.org/file/8-1650292x52.png" class="200" />
- 7.
>http://html.scirp.org/file/8-1650292x53.png" class="200" />
- 8.
>http://html.scirp.org/file/8-1650292x54.png" class="200" />
- 9.
>http://html.scirp.org/file/8-1650292x55.png" class="200" />
- 10.
>http://html.scirp.org/file/8-1650292x56.png" class="200" />
- (Line 1 follows from Leonard’s L9 and CnX. Line 7 follows from P1 and Line 6. Line 9 follows from Leonard’s formula L5. Other lines follow by propositional logic from previous lines.)
- B. Formula References
- In order to make this paper self-contained, we list here formulas from other sources that are referenced in the annotations of proofs.
- Formulas from (Leonard, 1969).
- L5.
>http://html.scirp.org/file/8-1650292x57.png" class="200" />
- L6.
>http://html.scirp.org/file/8-1650292x58.png" class="200" />
- L9.
>http://html.scirp.org/file/8-1650292x59.png" class="200" />
- D1.
>http://html.scirp.org/file/8-1650292x60.png" class="200" />
- Leonard claimed in (Leonard, 1969, page 58) that it was fifteen years before he accidentally hit upon L5 as a requisite for his logic.
- Formulas for forms of Obversion.
- Obversion in Leonard’s logic was discussed in (Jones, 1962). Here, as in Section 2 above, we do not attempt to formulate a minimal set of independent formulas. These formulas are chosen for convenience.
- Ob1.
>http://html.scirp.org/file/8-1650292x61.png" class="200" />
- Ob2.
>http://html.scirp.org/file/8-1650292x62.png" class="200" />
- Formulas from Jones (Jones, 1964).
- Def 2.
>http://html.scirp.org/file/8-1650292x63.png" class="200" />
- CnX.
>http://html.scirp.org/file/8-1650292x64.png" class="200" />
- Nc.
>http://html.scirp.org/file/8-1650292x65.png" class="200" />
- The lower-case letter c is used as a non-designating constant term for illustrative purposes.



 >http://html.scirp.org/file/8-1650292x40.png" class="200" />
>http://html.scirp.org/file/8-1650292x40.png" class="200" /> >http://html.scirp.org/file/8-1650292x41.png" class="200" />
>http://html.scirp.org/file/8-1650292x41.png" class="200" /> >http://html.scirp.org/file/8-1650292x42.png" class="200" />
>http://html.scirp.org/file/8-1650292x42.png" class="200" /> >http://html.scirp.org/file/8-1650292x43.png" class="200" />
>http://html.scirp.org/file/8-1650292x43.png" class="200" /> >http://html.scirp.org/file/8-1650292x44.png" class="200" />
>http://html.scirp.org/file/8-1650292x44.png" class="200" /> >http://html.scirp.org/file/8-1650292x45.png" class="200" />
>http://html.scirp.org/file/8-1650292x45.png" class="200" /> >http://html.scirp.org/file/8-1650292x46.png" class="200" />
>http://html.scirp.org/file/8-1650292x46.png" class="200" /> >http://html.scirp.org/file/8-1650292x47.png" class="200" />
>http://html.scirp.org/file/8-1650292x47.png" class="200" /> >http://html.scirp.org/file/8-1650292x48.png" class="200" />
>http://html.scirp.org/file/8-1650292x48.png" class="200" /> >http://html.scirp.org/file/8-1650292x49.png" class="200" />
>http://html.scirp.org/file/8-1650292x49.png" class="200" /> >http://html.scirp.org/file/8-1650292x50.png" class="200" />
>http://html.scirp.org/file/8-1650292x50.png" class="200" /> >http://html.scirp.org/file/8-1650292x51.png" class="200" />
>http://html.scirp.org/file/8-1650292x51.png" class="200" /> >http://html.scirp.org/file/8-1650292x52.png" class="200" />
>http://html.scirp.org/file/8-1650292x52.png" class="200" /> >http://html.scirp.org/file/8-1650292x53.png" class="200" />
>http://html.scirp.org/file/8-1650292x53.png" class="200" /> >http://html.scirp.org/file/8-1650292x54.png" class="200" />
>http://html.scirp.org/file/8-1650292x54.png" class="200" /> >http://html.scirp.org/file/8-1650292x55.png" class="200" />
>http://html.scirp.org/file/8-1650292x55.png" class="200" /> >http://html.scirp.org/file/8-1650292x56.png" class="200" />
>http://html.scirp.org/file/8-1650292x56.png" class="200" /> >http://html.scirp.org/file/8-1650292x57.png" class="200" />
>http://html.scirp.org/file/8-1650292x57.png" class="200" /> >http://html.scirp.org/file/8-1650292x58.png" class="200" />
>http://html.scirp.org/file/8-1650292x58.png" class="200" /> >http://html.scirp.org/file/8-1650292x59.png" class="200" />
>http://html.scirp.org/file/8-1650292x59.png" class="200" /> >http://html.scirp.org/file/8-1650292x60.png" class="200" />
>http://html.scirp.org/file/8-1650292x60.png" class="200" /> >http://html.scirp.org/file/8-1650292x61.png" class="200" />
>http://html.scirp.org/file/8-1650292x61.png" class="200" /> >http://html.scirp.org/file/8-1650292x62.png" class="200" />
>http://html.scirp.org/file/8-1650292x62.png" class="200" /> >http://html.scirp.org/file/8-1650292x63.png" class="200" />
>http://html.scirp.org/file/8-1650292x63.png" class="200" /> >http://html.scirp.org/file/8-1650292x64.png" class="200" />
>http://html.scirp.org/file/8-1650292x64.png" class="200" /> >http://html.scirp.org/file/8-1650292x65.png" class="200" />
>http://html.scirp.org/file/8-1650292x65.png" class="200" />