World Journal of Engineering and Technology
Vol.03 No.04(2015), Article ID:61172,14 pages
10.4236/wjet.2015.34023
Design Optimization of TBM Disc Cutters for Different Geological Conditions
Yimin Xia1, Kui Zhang1,2*, Jingsheng Liu2
1State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha, China
2School of Engineering, University of Hull, Hull, UK

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 September 2015; accepted 14 November 2015; published 17 November 2015
ABSTRACT
A novel optimization methodology for the disc cutter designs of tunnel boring machines (TBM) was presented. To fully understand the characteristics and performance of TBM cutters, a comprehensive list of performance parameters were investigated, including maximum equivalent stress and strain, specific energy and wear life which were closely related to the cutting forces and profile geometry of the cutter rings. A systematic method was employed to evaluate an overall performance index by incorporating objectives at all possible geological conditions. The Multi-objective & Multi-geologic Conditions Optimization (MMCO) program was then developed, which combined the updating of finite element model, system evaluation, finite element solving, post-processing and optimization algorithm. Finally, the MMCO was used to optimize the TBM cutters used in a TBM tunnel project in China. The results show that the optimization significantly improves the working performances of the cutters under all geological conditions considered.
Keywords:
Disc Cutter, Finite Element Method, Geological Condition, Structural Optimization, TBM

1. Introduction
With the mushrooming of tunneling projects for underground space in China, the full face rock tunnel boring machine (TBM) has become more important. As the key component installed on the cutter head of TBMs, a disc cutter (hereinafter referred to as a cutter) commonly consists of a cutter ring, a hub, a pair of tapered roller bearings and others (see Figure 1), of which the cutter ring directly interacts with rock and therefore plays a vital role in tunnel excavation. On one hand, a small deviation of some sensitive parameters of the cutter ring such as tip width will result in a significant change in rock-breaking forces and cutting efficiency [1] [2] ; on the other hand, wear characteristics of the cutter which have significant effects on tunneling cost and work period are closely related to profile geometry of the ring and geological conditions [3] . Considering that some components of commercial cutters such as bearings and seals have already been standardized and serialized in TBM industry nowadays, it is quite normal for designers to focus their attention on choosing an optimal profile of a cutter ring rather than on re-designing the whole cutter for a given tunnel project. Unfortunately, the complexity of the interaction between rock and cutter rings, as well as the diversity of geological conditions, represents great challenges in TBM cutter design. Especially with the inevitable trend in TBM applications toward long-distance tunneling, tougher geological conditions such as hydrostatic pressure, thermal environment, flowing soil and incredibly hard rock will further complicate the design process [4] .
In order to improve the cutters’ performance, some leading companies such as Robbins are being engaged in developing custom design solutions for cutters applied to soft rocks and mixed grounds [5] . European Union launched a long-term research program GOODLIFE (Global optimization of disc cutter tool life for TBMs, GRD1-1999-10335) which suggested the great potential for reducing excavation costs by some altering in cutter structures and in metallurgy. The Colorado School of Mines (CSM) model [6] , based on chip formation mechanism and linear cutting tests [7] , allegedly can determine the optimal geometry of cutter rings according to the rock property specified by users, but it seems to be only applicable to a single geological condition. Some researchers in related fields employed multi-objective genetic algorithm and cooperative co-evolutionary algorithm to solve cutters’ layout design problems [8] [9] , which shed light on the cutter design with multiple nonlinear constraints. However, these researches have the same shortcoming as the CSM model.
In this study, based on a theoretical cutting model, a comprehensive list of performance parameters were investigated, and then a systematic evaluation method was employed which could simultaneously review the parameters for all geological conditions. To solve these unique geology-related multi-factor optimization problems for TBM cutters, a novel design optimization methodology for different geological conditions, named Multi- objective & Multi-geologic Conditions Optimization (MMCO) was then developed. Finally, a case study was present. It is worth noting that in this paper we only focus our investigations on constant cross-section (CCS) cutters as they have higher cutting efficiency and longer-term durability comparing with V-shaped cutters [1] . The dimensional parameters of a CCS cutter are shown in Figure 1.
2. Cutting Model and Performance Parameters
2.1. Theoretical Cutting Model
The CSM model is one of the most well-known models in TBM industry. Using this model, the cutting forces can be estimated as a function of intact rock properties and the cutter geometry [10] . However, the shortcoming of the model is that it does not fully consider cutters’ movement characteristics. To overcoming the aforementioned issues, The Central South University (CSU) [11] model places particular emphasis on spiral characteristics of rock-breaking movement (see Figure 2 up); by solving the equilibrium equations of ideal two-dimension

Figure 1. Partial section view of a cutter and dimensional parameters of a CCS cutter ring.
Figure 2. The CSU model based on spiral characteristics of cutters’ rock- breaking movement.
debris (see Figure 2 down), the cutting forces can be formulated as the complicated functions Equations (1)-(3). The predicted cutting forces are in good agreement with the experimental values obtained from the cutting tests on the rotary cutting test platform, so it is quite reasonable to use this model to obtain the cutting forces for different geological conditions.
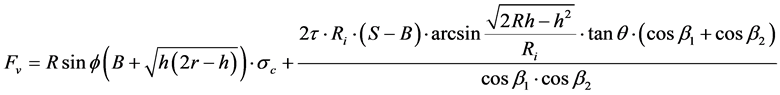 (1)
(1)
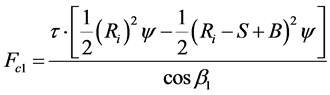 and
and  (2)
(2)
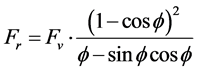 (3)
(3)
where Fv, Fc1, Fc2 and Fr are the vertical cutting force, the lateral force component near the central axis of the cutter head, the lateral force component far from the central axis and the rolling force respectively; B, h, r, R and θ are the tip width, the penetration depth, the transition radius, the external radius and the edge angle of the cutter ring; Ri is the installation radius of the ith cutter; S is the cutter spacing; β1 and β2 are the phase differences between the ith cutter and its adjacent cutters; σc and τ are the uniaxial compressive strength (UCS) and shear strength of rock respectively; φ is the contact angle of the cutter ring on rock surface; Ψ is the angle between two sidelines which is given by:
 (4)
(4)
2.2. Performance Parameters
Based on the above cutting model, a comprehensive list of performance parameters are chosen as follows:
1) Wear life Lw
Cutter wear incurs the cost of downtime as well as the cost of refurbishing and replacing cutters and therefore is a critical design factor. There are some semi-theoretical models available for predicting the wear life of cutter rings [12] - [15] , of which Wijk model [12] is one of the most comprehensive models. Based on the data collected from construction sites, Wijk drew the conclusion that Lw is approximately inversely proportional to CAI2 (Cerchar Abrasivity Index of rock [16] ) and (σcσt)1/2 which is a measure of the shear strength of rock τ; Lw is proportional to wear volume Vw and cutting pressure acting on the cutter tip Fv/B'. Incorporating all the assumptions above and introducing the wear coefficient Σ, Pa2/m then yields the following relation for the wear life Lw:
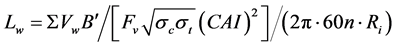 (5)
(5)
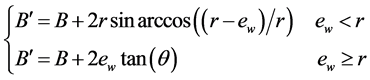 (6)
(6)
where B' is the tip width of the worn ring; ew is the radial wear of the cutter ring; n is the rotational speed of the cutterhead; σt is the uniaxial tensile strength of rock.
As Wijk model is originally deduced for V-shaped cutters, wear volume Vw should be further modified for CCS cutters. Assuming that the cutter tip of CCS cutters will still maintain CCS shape during the cutting process, wear volume Vw can be calculated according to the geometry of the worn cutter tip, as shown in Figure 3. Σ can be obtained by laboratory test or by fitting the wear data measured in-site.
2) Specific energy SE
As mentioned above, the cutting forces in the CSU model are derived from the equilibrium equations of the ideal two-dimension debris. According to tension-shear broken theory, there exist three types of debris due to non-overlapping, just-overlapping and overlapping crack, as shown in Figure 4. Based on the geometric relationship of each type, rock breaking volume co-produced by the ith cutter and its adjacent cutter V can be written in the form of piecewise functions as follows [17] :
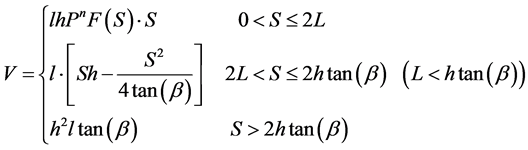 (7)
(7)
 (8)
(8)
Figure 3. Geometric illustrations of the worn cutter tip.

Figure 4. Illustrations of three types of debris due to non-overlapping, just-overlapping and overlapping crack.
where β is the rock crushing angle; L is the crack length which can be predicted by the semi-theoretical model based on the linear regression method [18] ; other symbols are explained in literature [17] .
SE is selected to assess the cutting efficiency of cutters. SE can be given as:
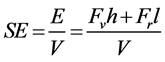
where l is the rolling length of the cutter.
3) Maximum equivalent stress σmax and maximum equivalent strain εmax
σmax and εmax are selected to check whether cutter rings can withstand the given cutting forces. Normally for a rolling cutter, a cutter ring is heated and then press-fitted into a mating hub which is slightly smaller than the ring so that an interference fit is created after the ring cools down. Undoubtedly, the initial stress condition caused by the interference fit will greatly affect the stress distribution and strength of the ring and thus should be considered. In this paper, σmax and εmax are obtained by solving the FE model to which both the calculated cutting forces and a recommended interference δmin are applied. To meet the demand of transferring torque and evening the stress distribution, the minimum magnitude of interference is set to 0.05 mm [19] .
4) Relative cost ΔC
With the help of prior knowledge, feature-based cost estimation techniques can assist designers to quickly estimate the manufacturing cost of a product at the conceptual design stage of the product life cycle [20] . It is assumed that machining parameters and materials remain the same, ΔC which is defined as the relative cost of a new cutter ring when compared with the original one can be easily estimated by:
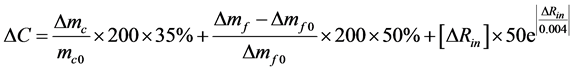
where 







Obviously, ΔC is not the true cost but an index which roughly indicates the economy of sizing/shape changes and provides the designers with a means of comparing the relative complexities of alternate designs. The coefficients in Equation (10) are provided by one of our partners, namely China Liaocheng RZ Construction Cutters Co., Ltd.
5) For lightweight design, the mass of the cutter ring mc is also selected as a design objective.
3. Structural Optimization of TBM Cutters
3.1. Systematic Evaluation Method
Based on the concept of parameter profiles [21] , an m ´ n matrix (dij) called performance data matrix (PDM) is defined by a set of performance parameters Pi 
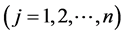

where lij and bij are the lower acceptable limit and the best expected value, respectively; for dij > bij, Dij = 10; and for dij < lij, Dij = 0. The data point for the cases of acceptable upper limit and double acceptable limits can be calculated in a similar way.
The mean and standard deviation (SD) are calculated for each parameter and geological condition in each column and row in the PPM. A well-designed cutter should have low SDs and high mean values (close to 10). The existence of high SDs signifies that the cutter is likely to have significant problematic areas. Therefore, the system may be reviewed by using these means and SDs as follows:
a) A high SD for a row indicates variable system performance under different geological conditions for a particular parameter.
b) A high SD for a column indicates that the system is likely to have significant problematic performance for the specific geological condition.
In order to get a more concise form, a parameter performance index for all possible geological conditions PPIi and a geological performance index GPIj for all parameters can be defined as follows:


The two indices are calculated by summing the inverse of the data points to avoid the effect of any particularly low scores being hidden by high scores in other respects which is possible when only the mean is calculated. For ease of analysis, the performance indices are brought into the range 0-10 no matter how many data points are used in each calculation. This enables different parameters and geological conditions to be compared in order to gain an overall perspective of the character of the design system. The system may be further reviewed by using this information as follows:
a) A comparison of PPIs will indicate whether the system performs better with respect to some performances than others.
b) A comparison of GPIs will show whether the system performs significantly better under some geological conditions than others.
Considering the PPI and GPI’s role, it is quite normal to integrate them to obtain a measure of the vulnerability of a particular parameter/geology combination. Each performance parameter or geological condition is weighted according to its importance, and the data points are calculated as:
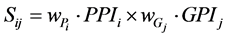
where 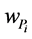
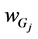


Based on the synthesis concept of design, an overall performance index (OPI) is selected to measure the design quality of the system:
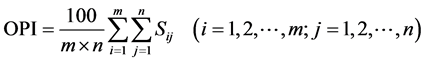
The OPI comprises all the performance parameters under a total of n geological conditions simultaneously, which reflects the closeness of the actual performance of design to the acceptable limit and the best value of the performance given by the designers. The evaluation method presented in this paper makes it possible to force some or all performances to approach their best level values.
3.2. Multi-Objective & Multi-Geologic Conditions Optimization (MMCO)
There are efficient optimization strategies which can produce a set of high-quality solutions for general design problems. For example, a multifactor (multi-objective and multi-loading-case) optimization method (called MOST-multifactor optimization of structure techniques) [21] - [23] , devolved by J.S. Liu et al., as originally developed to solve the structure design with strength/weight conflict, such as antenna systems and ultralight weight truss materials, is now updated to automatically accommodate and execute unique geology-related multi-factor optimization problems specially for TBM cutters. Unlike its predecessor, the updated one considers all the predicted geological conditions and their corresponding loading cases. In other words, the cutting load is now determined by rock properties and geological circumstances rather than simply given by designers. Therefore, the new program can comprehensively consider the coupling effects of the structural performance, rock-breaking mechanism and geological conditions. In order to facilitate the distinction between two programs, the new is called Multi-objective & Multi-geologic Conditions Optimization (MMCO).
Flow chart of MMCO is shown in Figure 5. MMCO systematically incorporates the FEA, system evaluation and optimization algorithm, including pre- and post-processing, input/output, model update and interface procedures. By employing ANSYS to carry out structural analyses under different geological conditions, together with theoretical analyses, the core optimization program can produce an optimal design based on the analysis results and optimization criteria. The optimization problem is solved to maximize the objective function by using the effective zero-order method which utilizes conjugate search directions.
4. Case Study
To illustrate what could be achieved in the performance improvement, the MMCO is performed for cutters originally used in a TBM tunnel project in China. By core drilling and laboratory tests, geological conditions encountered along the alignment of the tunnel mainly consist of four types of rock. Rock properties used to de-
Figure 5. Flow chart of MMCO (black dashed lines denote the data flow).
scribe the character of four geological conditions are listed in Table 1. Each condition is properly weighted according to its importance by the expert scoring method.
To draw a comparison, the value of profile geometry of the original cutter is treated as the initial input for optimization. Combining the design variables and performance parameters with specific boundaries, the optimization model is presented as follows:


The above model is coupled with a FE model (see Figure 6). In order to reduce the computational cost, a half model is parametrically established by reading the APDL input file. Two upper horizontal cross-sections of the cutter ring are fixed. The cutting forces are applied on the contact surface of the cutter ring with rock in the form of nodal forces. Meanwhile, the uniform radial nodal displacement δmin is applied on the nodes attached to the inner surface of the cutter ring to simulate the interference fit.
5. Results and Discussions
By performing the MMCO, the OPI increases from 0.37 to 2.53. Performance parameters of the original and optimized cutter for all geological conditions are presented in Table 2. Significant improvement in the design can be seen from the results, especially:
1) The maximum SE occurred at G3 is reduced from 5.86 Kwh/m3 to 4.00 Kwh/m3.
2) The maximum σmax occurred at G4 is reduced from 163 MPa to 87.5 MPa. Correspondingly, the maximum εmax is reduced from 0.79 × 10−3 to 0.425 × 10−3.
Figure 6. FE model of the cutter ring in ANSYS.
Table 1. Rock properties of four geological conditions.
3) More importantly, whilst all of those mentioned above are achieved, the shortest wear life of the cutter ring obtained at G4 is prolonged from 17.8 hours to 22.7 hours and the wear life in other geological conditions has also improved to a satisfactory level.
If the optimized cutter was used to replace the original cutter, a high-confidence 43.7% decrease in the total consumption of cutter rings during the tunneling period from 1st February 2011 to 29th March 2011 could be expected according to Equation (5). Comparing with the given acceptable limit 200, ΔC is rather small and acceptable.
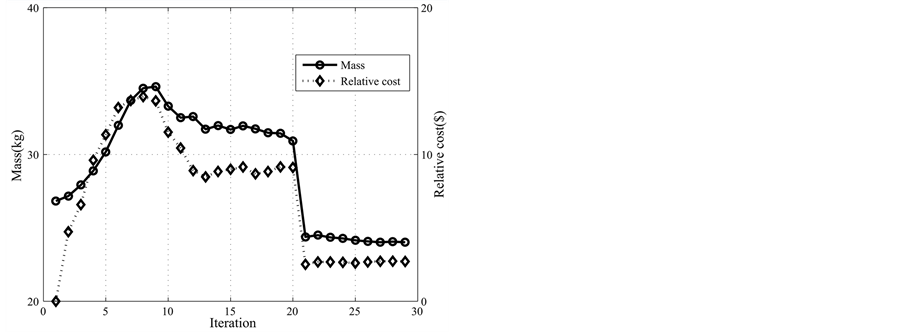
The optimization processes of all the performances are shown in Figure 7. These figures demonstrate the convergence history from the preliminary design to a much better design based on the optimization criteria. From these figures, a desired steady convergence can be observed.
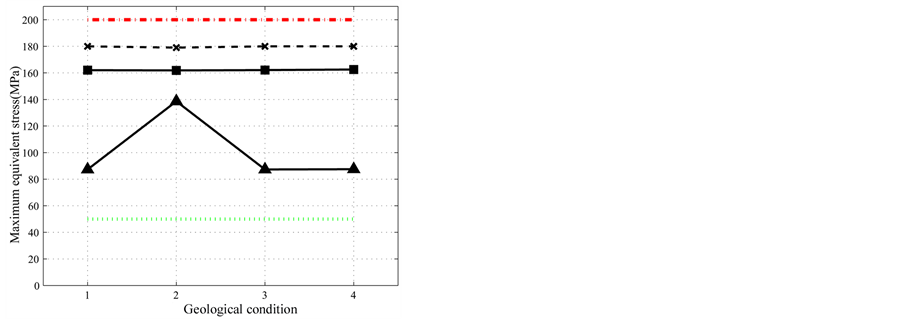
Figure 8 provides more complete comparisons of the cutter performances before and after the optimization
Figure 7. Convergence history under different geological conditions.
Figure 8. Comparison between the cutter performances before and after the optimization for all geological conditions.
Table 2. Optimization results (figures in parentheses denote the reduction/growth rates).
for all geological conditions considered. For the sake of comparison, the best expected values and the given acceptable limits on each performance parameter, as well as the cutter performances of a randomly selected cutter ring with a similar shape (hereinafter referred to as the similar cutter), are also illustrated in Figure 8. Notice that the similar cutter behaves poorly in most cases. Also worse still, its SE in G4 exceeds the upper limit, which means it is unsuitable for this project case. In addition, the original cutter is not very suitable for being used under all four geological conditions. A wild guess could then be made that the original cutter was just designed for a single ground in the 9# tunnel.
The SDs, PPIs and GPIs for the original and optimized cutter are listed in Table 3 and Table 4, which can separately provide an overall performance rating for each performance and each geological condition. As shown in Table 3, the lowest value of PPIs can be observed in the wear life for the two cutters, which indicates that the cutter’s performance is restricted by wear life. Actually, in most TBM tunneling project, of which four different tunneling projects in China is shown in Table 5, cutter change is always a time consuming activity which ring wear can have a major impact on. Similarly, G3 is one of the toughest geological conditions, which is consistent with the actual observation in the construction site. As the program can try to focus on strengthening ‘the weak spot’ under the worst geological condition as well as maximizing the overall performance, both PPI7 and GPI3 increase to a higher level.
The variations of the design variables before and after the optimization are listed in Table 6. It can be seenthat the tip shape of the optimized cutter is different from that of the original while their external dimensions are almost the same. This is because the MMCO has more design freedom and flexibility in the tip shape to which SE, Lw and structural strength might be more sensitive than ΔC and mc. In other words, great changes in the external dimensions such as R and Rin will incur large ΔC. It is also worth to note that all the three cutter designs have yielded the same external diameter (17 inch) of the cutter rings. Not coincidentally, this is a common size widely adopted by modern TBMs nowadays.
6. Conclusion
The TBM cutter optimization presented in this paper shows that the proposed MMCO method is very effective for the complicated design of cutters and has the potential to be further developed into a useful design tool. The optimization improves not only the cutter strength but also a comprehensive list of performance parameters which
Table 3. System parameter profile analyses of the original and optimized designs (non-dimensional).
Table 4. Geological condition profile analyses of the original and optimized designs (non-dimensional).
Table 5. Statistical comparison of cutter changes between four different tunneling projects in China [24] [25] .
Table 6. Design variables for the original cutter, the optimized cutter and the similar cutter.
are highly related to geological conditions and their corresponding loading cases. Like any other non-linear programming method, the proposed technique may not necessarily achieve a global optimum or force every performance at every geological condition to reach its optimum, especially when some objectives conflict with others and when many geological conditions are concurrently considered in an optimization. However, the MMCO results obtained for the case study show that performance of the optimized cutter has been improved significantly for all geological conditions. Based on its capability of MMCO in solving multi-objective and multi- geologic conditions problems, it will be the future work to develop it to optimize the whole cutterheads of TBMs.
Acknowledgements
The authors acknowledge the general manager of China Liaocheng RZ Construction Cutters Co., Ltd., Mr. Lei Chen who provided us useful guidance in cutter modeling. Also, the assistance and support of TBM Research Team in State Key Laboratory of High Performance Complex Manufacturing, including Prof. Qing Tan, Dr. Hao Lan, Zongming Zhu and Nianen Yi are much appreciated and acknowledged. The authors would also like to acknowledge the support of the Scholarship Award for Excellent Doctoral Student granted by Ministry of Education of R.P.C. and China Scholarship Council (CCS). This paper also is supported by the following grants: National Program on Key Basic Research Project of China (973 Program, 2013CB035401), National Natural Science Foundation of China (NSFC, 51475478), National High Technology Research and Development Program of China (863 program, 2012AA041801), Hunan Provincial Innovation Foundation for Postgraduate (CX2011B089), and Open-End Fund for the Valuable and Precision Instruments of Central South University (CSUZC2013013).
Cite this paper
Yimin Xia,Kui Zhang,Jingsheng Liu, (2015) Design Optimization of TBM Disc Cutters for Different Geological Conditions. World Journal of Engineering and Technology,03,218-231. doi: 10.4236/wjet.2015.34023
References
- 1. Acaroglu, O., Ozdemir, L. and Asbury, B. (2008) A Fuzzy Logic Model to Predict Specific Energy Requirement for TBM Performance Prediction. Tunnelling and Underground Space Technology, 23, 600-608.
http://dx.doi.org/10.1016/j.tust.2007.11.003 - 2. Rostami, J. and Ozdemir, L. (1993) A New Model for Performance Prediction of Hard Rock TBMs. Proceedings of the Rapid Excavation and Tunneling Conference, Boston, 13-17 June 1993, 793-793.
- 3. Gertsch, R., Gertsch, L. and Rostami, J. (2007) Disc Cutting Tests in Colorado Red Granite: Implications for TBM Performance Prediction. International Journal of Rock Mechanics and Mining Sciences, 44, 238-246.
http://dx.doi.org/10.1016/j.ijrmms.2006.07.007 - 4. Friant, J.E. and Ozdemir, L. (1993) Tunnel Boring Technology-Present and Future. Proceedings of the Rapid Excavation and Tunneling Conference, Boston, 13-17 June 1993, 869-869.
- 5. Lok (2011) Research and Development: A Sneak Peek at the Next Generation of Disc Cutters.
http://www.therobbinscompany.com/zh/blog/research-and-development/ - 6. Rostami, J., Ozdemir, L. and Nilson, B. (1996) Comparison between CSM and NTH Hard Rock TBM Performance Prediction Models. Proceedings of the Annual Technical Meeting of the Institute of Shaft Drilling Technology (ISDT), Las Vegas, 1-3 May 1996, 1-10.
- 7. Cho, J.W., Jeon, S., Jeong, H.Y. and Chang, S.H. (2013) Evaluation of Cutting Efficiency during TBM Disc Cutter Excavation within A Korean Granitic Rock Using Linear-Cutting-Machine Testing and Photogrammetric Measurement. Tunnelling and Underground Space Technology, 35, 37-54.
http://dx.doi.org/10.1016/j.tust.2012.08.006 - 8. Huo, J., Sun, W., Chen, J., Su, P. and Deng, L. (2010) Optimal Disc Cutters Plane Layout Design of the Full-Face Rock Tunnel Boring Machine (TBM) Based on A Multi-Objective Genetic Algorithm. Journal of Mechanical Science and Technology, 24, 521-528.
http://dx.doi.org/10.1007/s12206-009-1220-8 - 9. Sun, W., Huo, J., Chen, J., Li, Z., Zhang, X., Guo, L. and Zhao, Y. (2011) Disc Cutters’ Layout Design of the Full-Face Rock Tunnel Boring Machine (TBM) Using A Cooperative Coevolutionary Algorithm. Journal of Mechanical Science and Technology, 25, 415-427.
http://dx.doi.org/10.1007/s12206-010-1225-3 - 10. Yagiz, S. (2006) A Model for the Prediction of Tunnel Boring Machine Performance. Proceedings of 10th IAEG Congress, Nottingham, 6-10 September 2006, 1-10.
- 11. Xia, Y.M., Ouyang, T., Zhang, X.M. and Luo, D.Z. (2012) Mechanical Model of Breaking Rock and Force Characteristic of Disc Cutter. Journal of Central South University, 19, 1846-1852.
http://dx.doi.org/10.1007/s11771-012-1218-8 - 12. Wijk, G. (1992) A Model of Tunnel Boring Machine Performance. Geotechnical & Geological Engineering, 10, 19-40.
http://dx.doi.org/10.1007/BF00881969 - 13. Gehring, K. (1996) Performance and Cutter-Wear Prediction for Tunnel Boring Machines. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 33, 271A-271A.
http://dx.doi.org/10.1016/0148-9062(96)81919-X - 14. Bruland, A. (2000) Hard Rock Tunnel Boring. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim.
- 15. Frenzel, C. (2011) Disc Cutter Wear Phenomenology and Their Implications on Disc Cutter Consumption for TBM. Proceedings of 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, 26-29 June 2011, 1-7.
- 16. Rostami, J., Ozdemir, L., Bruland, A. and Dahl, F. (2005) Review of Issues Related to Cerchar Abrasivity Testing and Their Implications on Geotechnical Investigations and Cutter Cost Estimates. Rapid Excavation and Tunnelling Conference, Seattle, 27-29 June 2005, 15-29.
- 17. Zhou, X.W. (2010) Study on Disc Cutter Layout Optimization of Composite EPB Shield’s Cutterhead. Master Thesis, Central South of University, Changsha.
- 18. Liu, H.Y. (2004) Numerical Modelling of the Rock Fragmentation Progressive Process by Mechanical Tools. Ph.D. Thesis, Lulea University of Technology, Lulea.
- 19. Yimin, X., Wenhua, L., Jing, X., Tao, O. and Lei, C. (2010) Optimal Design Method of Magnitude of Interference for Disc Cutter Geology Adaptability. Proceedings of 2010 International Conference of the IEEE ICDMA, Changsha, 18-20 December 2010, 60-63.
http://dx.doi.org/10.1109/icdma.2010.273 - 20. Shehab, E.M. and Abdalla, H.S. (2001) Manufacturing Cost Modelling for Concurrent Product Development. Robotics and Computer-Integrated Manufacturing, 17, 341-353.
http://dx.doi.org/10.1016/S0736-5845(01)00009-6 - 21. Ket Thein, C. and Liu, J.S. (2012) Effective Structural Sizing/Shape Optimisation through A Reliability-Related Multifactor Optimisation Approach. Multidiscipline Modeling in Materials and Structures, 8, 159-177.
http://dx.doi.org/10.1108/15736101211251194 - 22. Liu, J.S. and Lu, T.J. (2004) Multi-Objective and Multi-Loading Optimization of Ultralightweight Truss Materials. International Journal of Solids and Structures, 41, 619-635.
http://dx.doi.org/10.1016/j.ijsolstr.2003.10.003 - 23. Liu, J.S. and Hollaway, L. (1998) Integrated Structure-Electromagnetic Optimization of Large Reflector Antenna Systems. Structural optimization, 16, 29-36.
http://dx.doi.org/10.1007/BF01213997 - 24. Jin, Y.Q., Liu, Z.H., Yang, L. and Zheng, G.S. (2011) Analyzing the Cause of TBM Disc Cutter Worn in Tao River Diversion Project No. 9 Tunnel. Construction Mechanization, 6, 79-81.
- 25. Zhou, Y.L. (2007) Quality Control for Rotary Hob of Tunnel Boring Machine and Its Checking and Repair Technology. Construction Machinery Technology & Management, 10, 85-92.