Received 23 September 2014; revised 18 October 2014; accepted 5 November 2014

ABSTRACT

The paper presents the vibration control for two air compressors used in tandem to an oxygen generating station. The compressors are identical in terms of constructive and functional proper- ties, and are both located on similar foundations. Each compressor is supported on a foundation made from one massive block of concrete, provided with some elastic and damping parts. This anti vibrating structure insulates the machines compared to other station equipment. During opera- tion, were observed dangerous levels of vibration at one of the machines, which forced some un- wanted stoppages for the station. Two hypotheses have been promoted. One of them referred to a pronounced wear of one compressor, although this was relatively new. The second hypothesis has taken in consideration the appearance of some cracks in the foundation massive concrete block. Experimental research conducted on the spot led to the identification of some errors done at foundation fabrication. The experimental results and some theoretical investigations are pre- sented in this paper.

Keywords:

foundation, harmonic disturbing Forces, Amortized forced Vibration, Vibration isolation, Coefficient of transmissibility

1. Introduction

In general, operating industrial equipments produce vibrations under the action of some disturbing forces. These are usually, periodic time dependent external forces. Common source for disturbing forces are the inertia forces. Virtually every moving body―(movements like: rotation, linear displacement, linear―alternative, oscillatory etc.)―is subject to inertial forces and therefore produces vibrations [1] and [2] .

Vibrations are transmitted to the foundation on which is installed the equipment. From dynamic stability con- siderations, these vibrations should be isolated. To isolate the vibrations it means to identify some technical measures, so that the foundation does not vibrate when the industrial equipment creates these forces. So, is re- quired that the disturbing forces transmitted to the foundation to be zero or as low as possible with the help of some damping measures [3] .

In the paper we studied a real case that occurred to an oxygen station. The replacement of two air compressors with a new model concurrently with restoration the foundation had generated unforeseen situation. During commissioning tests, there were identified dangerous levels of vibration which led the temporary shutdown of the compressors, and thus the oxygen station. In this context, our research team was asked to correct the non- compliance.

2. Theoretical Considerations on Forced Vibration

A particular important case in practical applications is the situation where the damping forces are negligible and over the mechanical system is acting only the disturbing force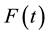. Being independent of system characteris- tics, the differential equation of motion is [4] and [5] :

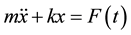(1)

where―the mass of the mechanical system (industrial equipment);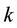―the elastic constant of the mechani- cal system;―coordinate of motion.

In practice, is often encountered situations where the disturbing force is harmonic. If the pulsation of this force is, then equation (1) is:

(2)

This equation has the particular solution

(3)

where―the amplitude for the forced vibration in the mechanical system;―the amplitude of the vibra-

tion; Substituting (3) in (2) and putting condition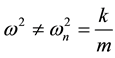, we obtain:

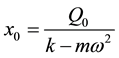(4)

With the notation, where is the static deformation of the vibrating system under the action of a

disturbing force equal with the maximum value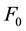, Equation (4) can be written in dimensionless [3] :

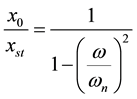(5)

We can observe that the amplitude of vibration depends by the pulsation ratio. This dependence is

shown in Figure 1 [6] .

Note that for, is positive and represents the forced vibration amplitude, being higher than.

In this situation, the forced vibration and disturbing force are in phase.

For, is negative. In this case the forced vibration and disturbing force are out of phase with,

or they are in opposition. The vibration amplitude is, but for the vibration study we will suppress the nega-

tive sign and we will consider the dashed drawn curve (see Figure 1).

For, i.e. for low frequency of disturbing forces, the forced vibration amplitude is greater than.

For high frequencies, the amplitude is less than and tends to be zero when tends to be.

In the point a, the disturbance force frequency is very low, and the mechanical system vibrates in phase with the force with the amplitude equal to. In the point b, the amplitude of forced vibration is very small. The force varies so rapidly that mechanical system does not have time to follow it. Basically, the system remains in relative rest. The point c, where, corresponds to the phenomenon of resonance. The vibration amplitudes increase together with the forces of the mechanical system. If these forces exceed the limit values for the strength of the mechanical structure, the system can be destroyed irreversibly. For this reason, the design of industrial equipment and foundation, take into account the phenomenon of resonance.

Resonance is practically avoided either by changing frequency for disturbing force when it coincides with the resonance frequency, either by modifying the structure of the system, by modifying the parameters and. The second situation includes also the computation for the foundation isolation [1] and [7] .

3. Theoretical Considerations on Vibration Isolation

To reduce or eliminate the forces transmitted to the foundation, it is inserted between the mechanical system and foundation different elastic materials: metal coil springs, cork, rubber, polystyrene, expanded sheets etc. If we note with the elastic constant of the materials inserted between the mechanical system and the foundation, and with mass of the industrial equipments, then the mechanical model is presented in Figure 2 [3] .

Transmissibility coefficient, namely ratio between the maximum of force transmitted with foundation and disturbing force, is given by dimensionless relation (5). As seen from Figure 1, in order as force transmitted to foundation to be as small as possible, the ratio must be as high as possible. This is done

basically by adopting constructive solutions with their own pulsation as small as possible, (i.e.

springs supple with elastic constant k small).

If industrial equipment is placed directly on the foundation without elastic elements, , and, so the seating basis is rigid, the transmissibility coefficient, and disturbing forces are trans- mitted entirely to the foundation.

For, the transmissibility ratio is. In this situation, whether there are introduced elastic mate- rials, the results increase the forces transmitted to the foundation. The effect is more pronounced if the pul- sation is close to the resonant pulsation. Then transmissibility coefficient becomes very large, and the forces transmitted to the foundation, are very dangerous. Therefore, in the foundation structure, vibration isolation measures are introduced, in addition to elastic materials and viscous damping elements. The differen- tial equation of vibration movement in this case is [2] :

(6)

where is the damping coefficient.

If disturbing force is harmonic, namely, then forced vibrations as solution of Equation (6) is:

(7)

where is the initial phase at moment and is obtained from

(8)

At resonance, the maximum forced amplitude is given [6]:

(9)

where is the critical damping coefficient, being equal to:

(10)

Discussions:

・ In case, the movement is not vibratory, but atypical. Mechanical system slowly approach to the rest position due the very high forces created by the insulation structure.

・ Where, the mechanical system movement is also atypical and it slowly approach the rest position.

・ If, mechanical system approaches rest position in the time interval called the relaxa- tion period.

In the forced harmonic motion of industrial equipment, damping force lags by an angle compared with elastic force. For this reason, the maximum force that is transmitted to the foundation will be [2] and [3] :

(11)

4. Mathematical Modeling of the Air Compressor Unit

The mechanical model for vibration and isolation with elastic elements and damping viscous elements is pre- sented in Figure 3 [3] and [8] .

The curves from the diagram of transmissibility coefficient (see Figure 3(b)) show the effect of damping forces, which is a reduction for the amplitude of forced vibration.

The vibration amplitude not becomes infinitely larger comparing with the case when and when. The other curves present maximum of amplitudes with decreasing values, if increase, given by rela- tionship:

(12)

The machines for compressing air and its mounting scheme on the foundation are presented in Figure 4. A multi-cylinder compressor, as a five stage air compressor 1, is composed from two parts, law pressure stage (cy- linders I, II and III) and high pressure stage (cylinders IV and V), both being driven by an electric machine 2 via an elastic coupling. All ensembles are fixed on a massive block of concrete 3 which is seating on the foun- dation 5. Between the block 3 and the foundation was interposed an elastic and damping structure 4.

The massive block foundation is used for two reasons: to machine axis line stiffening and to diminishing ma- chine-foundation vibration excited by residual inertial unbalanced forces, acting on machine [9] . The vibration levels depend on the dynamic characteristics of the elastic and damping structure 4 and on the in- ertial mass of the massive concrete block 3.

To determined the distribution of vibration was measured the vibration motions components, , and, in a lot of points along the ensemble machine massive foundation. For the motion of a rigid body, the distribution of vibration occurs is [8] and [10] :

(13)

where is the column vector matrix for the resultants vibration, and is given by:

(14)

・ is the column vector matrix of vibration point at radius -compared to the geometric centre 0

of the structure;

・ is the column vector matrix of “out of phase” at point compared to the reference system X0YZ-

chosen arbitrarily and is given by:

(15)

・ is the matrix of position point compared to the reference system X0YZ and is:

(16)

Distribution law for the rigid body vibration given by relationship (13), can be extended to the distribution of amplitudes:

(17)

where with the letters and are meaning the terms and.

5. Experimental Researches

Experimental investigations have been focused on study of isolating vibration for two air compressor units from an oxygen station. Although the two aggregates were identical in terms of construction and were also placed on the identical foundations, one of them presented higher levels of vibration than the other.

Was emitted the hypothesis that one of aggregates had hidden defects at installation, which led to its prema- ture wear. But the two aggregates were new, and verification tests done before entering into service did not re- veal any hidden defect.

Has been also hypothesised that the concrete massive block interposed between aggregate and foundation, has “cracked” during the technological tests, and as result it was amplifying the disturbance forces generated by the mechanical (vibrating) system.

In the first phase was carried out a dimensional static verification of the two units, but no structural differ- ences were found between them. Tolerances of the active elements―pistons, cylinder shirts, rod-crank mechanism have been found to be into the prescribed limits. There were not found abnormal wear of these compo- nents and the mechanism rod-crank it is was working smoothly, evenly and without shocks at change of di- rection.

These results had supported the hypothesis that disruptive forces are the same for both aggre- gates. To explain the large difference between the vibrations of the two units was placed the emphasis in the second phase of experimental research, it was performed integrity verification for the foundation. This was as- similated to a massive mass that must have the vibration motion of a rigid body. In the case of some hidden cracks, significant deviations from the rigid body anticipated movements will be present.

To determine the vibration distribution, we measured the components for the vibration movements, and―see relationship (14)―for several points along the perimeter of aggregates placed on the solid concrete block of the foundation (see Figure 4).

The experimental measurements we made with a comprehensive installation type DELTA TRON^®, have al- lowed the effective determination of vibration amplitudes, and out of phase according to the model shown in Figure 4. The vibration motion distribution for the two air compression machines is shown in Figure 5.

Were used 8 tri-axial transducers for vibration monitoring, emplaced on the massive concrete block 3―in two parallel planes. It has been established one rectangular system X0YZ shown in the figure, as a reference basis for the reported measured vibration parameters.

The values for the vibration motion amplitude and out of phase for the first harmonic, corresponding to the two machines are given in the table below:

If we analyze these results, we cannot observe significant differences between the two aggregates. Therefore the hypotheses of premature wear, or the hypothesis of some cracks in the massive concrete block at one of the two units, were rejected.

Experimental researches performed in a longer time, showed however, random occurrence of some dangerous frequencies at different moments and speeds for the electric motor 2. Because the disturbance forces are acting periodically on the foundation with the pulsation, and because the force transmitted to the foundation did not exceed the maximum allowable limit, it was advanced the hypothesis of a variable damping force acting randomly in time. The coefficient of transmissibility determined by relation (5) has, therefore, a va- riable character.

This hypothesis was accepted by the oxygen station management, which has assumed responsibility for the foundation work quality. Due to the difficulties encountered during the work for gravel compaction, it was not followed exactly the technological recipe at one of the two foundations.

6. Conclusions

The study on vibration isolation has highlighted the importance of a strict compliance with the technical re- quirements for the foundation execution technology. To explain the large difference between vibration of the two aggregates, we focused on the integrity of the concrete foundation verify which as a massive mass must to has vibration of rigid body motions. In case of a possible hidden crack the significant deviation from the rigid body motions may occurs.

The damping forces variation during operation of the equipment, leads to some variations for the transmissibility coefficient values (see Figure 3(b)):

・ For, coefficient of transmissibility is higher than one, regardless of the ratio; which in-

cludes the case of resonance, viscous damping is advantageous because it reduces the transmissibility coeffi-

cient and therefore the amplitude of vibration;

・ For, coefficient of transmissibility is less than one, and it is lower for foundations with elastic elements only, and increases with the ratio; in this field, damping effect is unfavorable, so that for this situation―are preferred constructive solutions with materials with smaller elastic constant.

・ Whereas in the period starting and stopping, industrial equipments are passing through critical speeds, there is the possibility of the uncontrolled appearance of some dangerous vibrations; for this reason is recommended to use viscous damping with ratio as small as possible or at most equal to 0.5.

References