Advances in Materials Physics and Chemistry
Vol. 2 No. 3 (2012) , Article ID: 23223 , 4 pages DOI:10.4236/ampc.2012.23024
Ab Initio Study of Electronic Properties of a Armchair (7,7) Carbon Nanotube
Department of Physics, Shahid Chamran University of Ahvaz, Ahvaz, Iran
Email: salehi_h@scu.ac.ir
Received May 8, 2012; revised June 17, 2012; accepted June 23, 2012
Keywords: band gap; electronic structure; WIEN2k; FP-LAPW
ABSTRACT
The electronic structure, band gap and density of states of (7,7) Armchair carbon nanotube by the full potential-linearized augmented plane wave (FP-LAPW) method in the framework density functional theory (DFT) with the generalized gradient approximation (GGA) were studied. The calculated band structure and density of state of Armchair (7,7) carbon nanotube were in good agreement with theoretical and experimental results.
1. Introduction
Since their accidental discovery by Sumio Iijima of NEC in 1991 [1], carbon nanotubes have been of great interest both from a fundamental point of view and for future applications. Single Walled Nanotubes (SWNT) can be considered as long wrapped graphene sheets. nanotubes generally have a length to diameter ratio of about 1000 so they can be considered as nearly one-dimensional structures [2]. The most eye-catching features of these structures are their electronic, mechanical, optical and chemical characteristics, which open a way to future applications. Metallic CNTs have been suggested as an interconnect material due to their high current carrying capacity and mechanical stability [3]. Due to strong sp2 bonding (like graphite), carbon nanotubes can carry very high current densities [4]. Metallic single-walled have been shown to be able to carry extremely high current densities of the order of 109 A/cm2 [5]. A graphene sheet is a semi-metallic material with a zero band gap. The electronic states of an infinitely long nanotube, constructed from this sheet, are continuous along the nanotube axis but are quantized along the circumference. For an (n,n) armchair tube, there always exist electronic states that cross the corner points of the first Brillouin zone and hence these nanotubes always show a metallic behaviour. For an (n,m) tube, if (n − m)/3 ≠ an integer, the electronic states miss the corner points, and these nanotubes are semiconductors with a band gap that scales with the diameter of the tube (d) as 1/d and is of the order of 0.5 eV. For an (n,m) tube with (n − m)/3 = an integer, on the other hand, certain electronic states land on the corner points, and these nanotubes would be semimetallic, but they become small-band semiconductors due to curvature-induced rehybridization [6].
Since the discovery of carbon nanotubes, the fabrication of nanometer-scaled one-dimensional materials has attracted considerable interest due to their potential use in both nanotechnology and nano scale engineering. The stability and quasi-one dimensional nature of singlewalled carbon nanotubes (SWCNTs) make them unique systems from the experimental and theoretical points of view [7-10].
In this work we have carried out a first principles calculation on the electronic structure and density of state of CNT (7,7). Our results reveal that these structures have conducting behavior.
2. The Calculation Method
Calculation of the electronic band structure, local and total density of states of Armchair (7,7) Carbon nanotube, were carried out with a self-consistent scheme by solving the Kohn-Sham Equation using aFP-LAPW method in the framework of theDFT along with the GGA method by WIEN2k package [11-13]. In the FP-LAPW method, space is divided into two regions, a spherical “muffin-tin” around the nuclei in which radial solutions of Schrödinger Equation and their energy derivatives are used as basis functions, and an “interstitial” region between the muffin tins (MT) in which the basis set consists of plane waves. There is no pseudopotential approximation and core states are calculated self-consistently in the crystal potential. Also, core states are treated fully relativistically while valence and semi-core states are treated semirelativistically (i.e. ignoring the spinorbit coupling). The cut-off energy, which defines the separation of the core and valance states, was chosen as –9 Ry. In this calculation the convergence parameter, Rkmax = 5.5 was chosen. The value of the parameter Rkmax controls the size of the basis sets in these calculations. the others parameters are: Gmax = 12 and RMT(C) = 1.3 a.u. The self-consistent process, for (7,7) Armchair carbon nanotube, after 11 cycles had convergence of about 0.00001 in the eigenvalues in which were produced. For partial waves in atomic spheres, maximum L value is 10 and for partial waves in non muffin-tin calculations, maximum value of L is 4.
3. Results
3.1. Electronic Structure
The calculated structure for a (7,7) Armchair nanotube are shown in Figure 1. The structure of CNT (7,7) in this work is tetragonal unit cell and z-direction is chosen as tube axis (Figure 1). The total number of k-point in the first Brillouin zone (BZ) is taken to be equal to 100 and 11,200 is the k-point set mesh. By optimization of the lattice constants respect to the total energy we found that 8 Å vacuum (nanotube separation) in the lateral directions would be enough to avoid artificial tube-tube interaction. Therefore, the calculations were done for the tube arranged in array as shown in 2 × 2 × 2 repeated of single nanotube (Figure 1).
3.2. Band Structure
The calculated electronic structure of the CNT (7,7) carbon nanotoube in the high-symmetry directions in the Brillouin zone (BZ) is shown in Figure 2. The Fermi energy level is set to zero. The energy scale is in eV and the origin of energy was arbitrarily set to be at the maximum valence band (zero of energy).
The energy band gaps obtaind from different SWCNTs are given in Table 1. These values are compared with pre-
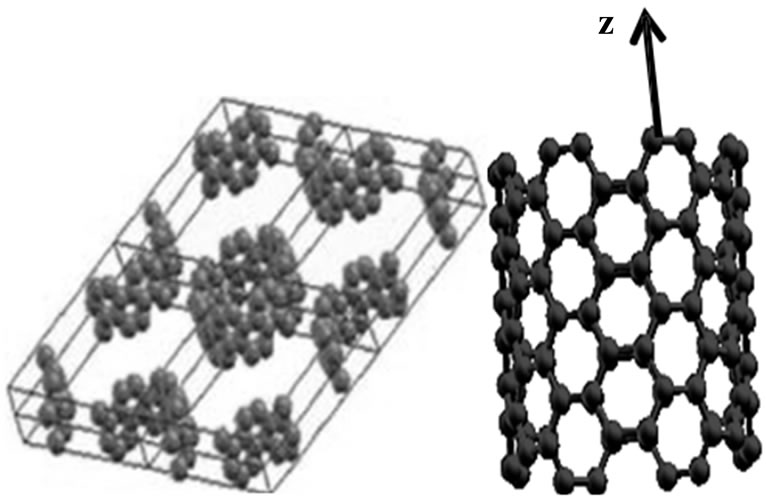
Figure 1. Periodicity 2 × 2 × 2 repeated of this single nanotube with tetragonal unit cell.

Figure 2. The calculated electronic band structure for CNT (7,7) (this work), (13,0), (9,9). The zero of the energy was set at top of the valence band [14].
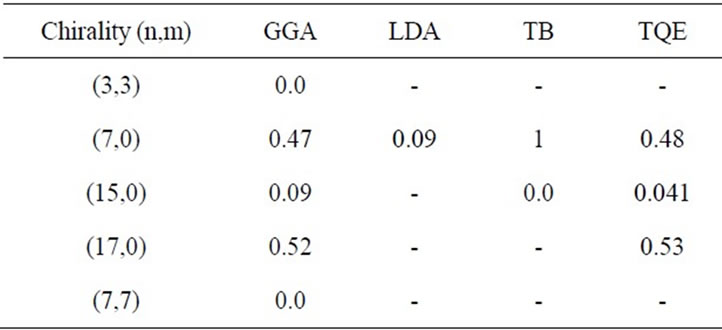
Table 1. The results for the band gap calculated by this method and others.
vious studied. It is seen that our results agree favourablywith past results.
The electron distribution in an energy spectrum is described by the density of states (DOS) and can be measured in photoemission experiments. The total DOS spectrum of Armchair (7,7) nanotube from −7 eV to 20 eV is shown in Figure 3. The Fermi energy level is set to zero.
The electronic band structure and DOS show that a (7,7) nanotube is a metallic nanotube with zero band gap and the valence and conduction bands cross each other at the Fermi level which is in agreement with the previous results [15,16]. The electronic band structure and DOS show that a (7,7) nanotube is metallic with zero band gap and the valence and conduction bands cross each other at the Fermi level.
To obtain a measure of the contribution of different atomic states in the band structure and also their possible hybridizations we made a detailed study of the local density of the states (figure 4).
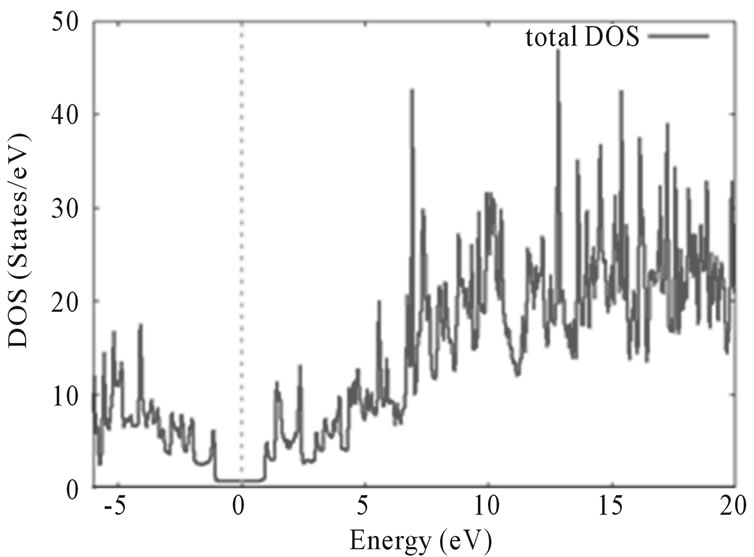
Figure 3. The total DOS for CNT (7,7).
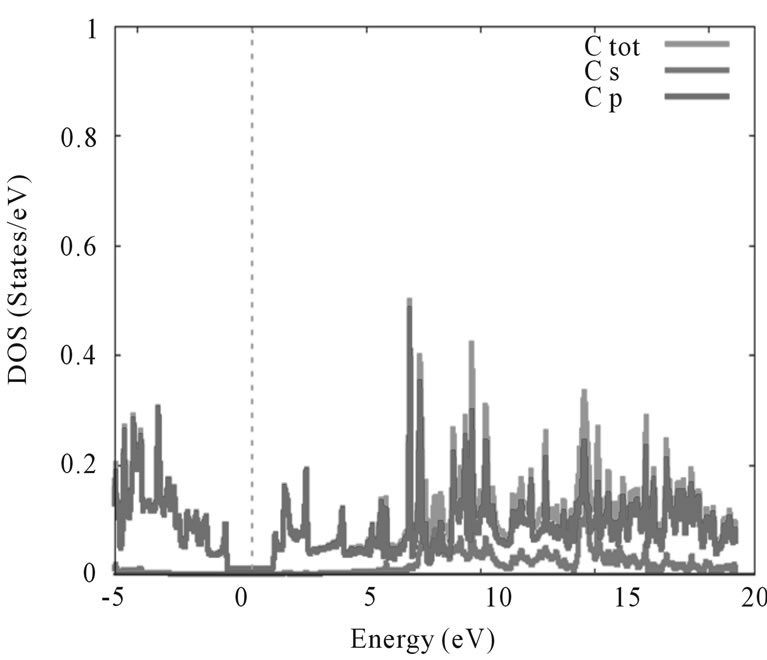
Figure 4. The local densities of states (LDOS) showing the contributions of CNT (7,7) atomic states.
Our calculations show that the tube is in agreement with the previous reported results [15-17].
4. Conclusion
The electronic properties of SWCNTs are strongly dependent on tube geometry. We have investigated the electronic band structure, local and total density of states of Armchair (7,7) Carbon nanotube using density functional theory as implemented in the code WIEN2k. These results predict that the nanotube have metallic behavior which confirms the prediction. In this work, our results are comparable with the values obtained with different experimental.
REFERENCES
- S. Iijima, “Helical Microtubules of Graphitic Carbon,” Nature, Vol. 354, 1991, pp. 56-58. doi:10.1038/354056a0
- M. Daenen, R. D. de Fouw, B. Hamers, P. G. A. Janssen, K. Schouteden and M. A. J Veld, “The Wondrous World of Carbon Nanotubes,” Eindhoven University of Technology, Eindhoven, 2003.
- F. Kreupl, et al., “Carbon Nanotubes in Interconnect Applications,” Microelectronic Engineering, Vol. 64, 2002, pp. 399-408. doi:10.1016/S0167-9317(02)00814-6
- B. Q. Wei, et al., “Reliability and Current Carrying Capacity of Carbon Nanotubes,” Applied Physics Letters, Vol. 79, No. 8, 2001, pp. 1172-1174. doi:10.1063/1.1396632
- M. Radosavljevic, et al., “High-Field Electrical Transport and Breakdown in Bundles of Single-Wall Carbon Nanotubes,” Physical Review B, Vol. 64, 2001, Article ID: 241307.
- H. Dai, “Carbon Nanotubes: Opportunities and Challenges,” Surface Science, Vol. 500, No. 1, 2002, pp. 218- 241. doi:10.1016/S0039-6028(01)01558-8
- S. Tasaki, K. Maekawa and T. Yamabe, “π-Band Contribution to the Optical Properties of Carbon Nanotubes: Effects of Chirality,” Physical Review B, Vol. 57, No. 15, 1998, pp. 9301-9318. doi:10.1103/PhysRevB.57.9301
- I. Bozovic, N. Bozovic and M. Damnjanovic, “Optical Dichroism in Nanotubes,” Physical Review, Vol. 62, No. 11, 2000, pp. 6971-6974. doi:10.1103/PhysRevB.62.6971
- O. E. Alon, V. Averbukh and N. Moiseyev, “High Harmonic Generation of Soft X-Rays by Carbon Nanotubes,” Physical Review B, Vol. 85, No. 24, 2000, pp. 5218-5221. doi:10.1103/PhysRevLett.85.5218
- E. L. Ivchenko and B. Spivak, “Chirality Effects in Carbon Nanotubes,” Physical Review B, Vol. 66, 2002, pp. 155404-155409. doi:10.1103/PhysRevB.66.155404
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, “Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation,” Physical Review B, Vol. 46, No. 11, 1992, pp. 6671-6687. doi:10.1103/PhysRevB.46.6671
- M. Peterson, F. Wanger, L. Hufnagel, M. Scheffler, P. Blaha and K. Schwarz, “Improving the Efficiency of FP-LAPW Calculations,” Computer Physics Communications, Vol. 126, No. 3, 2000, pp. 294-309. doi:10.1016/S0010-4655(99)00495-6
- P. Blaha and K. Schwarz, “WIEN2k,” Vienna University of Technology, Vienna, 2008.
- T. Movlarooy, A. Kompany, S. M. Hosseini and N. Shahtahmasebi, “Optical Absorption and Electron Energy Loss Spectra of Single-Walled Carbon Nanotubes,” Journal of Computational Materials Science, Vol. 49, 2010, pp. 450-456. doi:10.1016/j.commatsci.2010.05.035
- D. J. Mowbray, C. Morgan and K. S. Thygesen, “Influence of O2 and N2 on the Conductivity of Carbon Nanotube Networks,” Physical Review B, Vol. 79, 2009, Article ID: 195431. doi:10.1103/PhysRevB.79.195431
- Y. Maeda, Sh. Kimura, M. Kanda, Y. Hirashima, T. Hasegawa, T. Wakahara, Y. Lian, T. Nakahodo, T. Tsuchiya, T. Akasaka, J. Lu, X. Zhang, Z. Gao, Y. Yu, Sh. Nagase, S. Kazaoui, N. Minami, T. Shimizu, H. Tokumoto and R. Saito, “Large-Scale Separation of Metallic and Semiconducting Single-Walled Carbon Nanotubes,” Journal of the American Chemical Society, Vol. 127, 2005, pp. 10287- 10290. doi:10.1021/ja051774o
- W. Zhu, X. Yan and Y. Xiao, “Hexagonal Silicon Nanotube Confined inside a Carbon Nanotube: A First-Principles Study,” Physics Letters A, Vol. 372, 2008, pp. 1308- 1312. doi:10.1016/j.physleta.2007.09.017

