Received 6 July 2015; accepted 2 August 2015; published 5 August 2015

ABSTRACT

This paper investigates time-consistent plans by incorporating the reference-dependent consumption model with endogenous labor supply. To what extent these plans can help the consumer overcome the double self-control problems of over-consumption and late-retirement is discussed. The consumption level and labor supply of the preferred personal equilibrium solution are compared with those of ex-ante optimal solution and present-biased solution. For all preferred personal equilibrium plans, both consumption level and labor supply are lower than those of the consumer who is present-biased but without reference-dependent preference. Although the preferred personal equilibrium solutions do not include the ex-ante optimal level, they help mitigate the welfare loss caused by present bias.

Keywords:

Reference-Dependent Preference, Endogenous Labor Supply, Time Consistency, Self-Control

1. Introduction

People usually desire immediate gratification but underrate the wellbeing in the future. This present-biased preference causes self-control problems. To overcome the self-control problem, internal commitment devices are often employed, such as goals and self-rewards (Hsiaw, 2013 [1] ; Koch et al., 2014 [2] ; Koch and Nafziger, 2011 [3] ).

An individual with present-biased preference suffers from double self-control problems of over-consumption and late-retirement (Diamond and Köszegi, 2003 [4] ; Zhang, 2013 [5] ). Meanwhile, reference-dependent preference (Köszegi and Rabin, 2009 [6] ) captures the feature that people derive utility by using rational expectations as the reference point. The inclusion of loss aversion which is rooted in the prospect theory (Kahneman and Tversky, 1979 [7] ) provides people with a motivation to overcome self-control problems. This paper aims to investigate that to what extent the double problems of over-consumption and late-retirement can be mitigated by a single time-consistent plan of an individual with reference-dependent consumption preference.

In this model, quasi-hyperbolic discounting is employed to approximate present-biased preference. The ex-ante perspective in the first period is optimal in the long run. In order to identify the time-consistent plan solution, referred as the preferred personal equilibrium (PPE) by Köszegi and Rabin (2009) [6] , this paper discusses the scenario that forms this equilibrium. This paper also investigates the PPE solutions corresponding to each degree of present bias by jointly considering consumption and working behavior. Through comparative statics, it is shown that these time-consistent plan solutions can alleviate the double self-control problems caused by present bias. However, the ex-ante optimal consumption plan is always time inconsistent, which is different from Köszegi and Rabin (2009) [6] .

The main novel point which makes the results of this paper different from Köszegi and Rabin (2009) [6] and other studies is that endogenous labor supply is incorporated. Hence, in this model the consumer who makes time-consistent plans is facing double self-control problems: over-consumption and late-retirement at the same time. Therefore, for a PPE consumption plan, the consumer does not only have to decide the consumption allocation, but also the retirement timing. In other words, the equilibrium consumption plans help a rational consumer regulate herself in two aspects: saving more and working shorter, but not back to the optimal level in the long run. In this context, this paper underlines the importance of rational plans, and also provides an explanation for that even if a rational individual can be failed in complete self-control.

Furthermore, the following novel points are also made. First, for a time-consistent PPE plan, the reference- dependent preference is a factor which helps the consumer overcome her self-control problem. In this model, the consumer is facing double problems, but her instrument (the plan, or the “goal” as in Hsiaw, 2013 [1] ; Koch et al., 2014 [2] ; Koch and Nafziger, 2011 [3] ) is only one. This paper shows that the single plan of consumption cannot help the consumer overcome the double self-control problems completely. This result is hardly ever discussed by the related studies. Second, the reference-dependent preference is domain dependent in that only the consumption involves gain-loss utility.

2. The Model

Consider a representative consumer who lives for three periods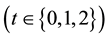. In period 0, the consumer doesn’t

consume or work, but she can form a consumption plan for the next periods. The consumer decides labor supply l in period 1 with wage rate 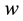given, and allocates the consumption between periods 1 and 2. Variable 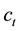(t = 1, 2) denotes the consumption level in each period. The intertemporal budget constraint is

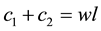. (1)

The consumer has present-biased preference. Following Laibson (1997) [8] , her life-time utility function with quasi-hyperbolic discounting is

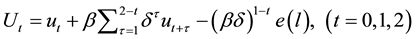. (2)

For simplicity, the long-run discount factor 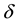is set to be 1. Present-bias parameter 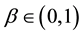captures the consumer’s impatience for immediate satisfaction. e(l) denotes the consumers disutility of working in period 1. Assume that the disutility function of working is convex.

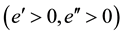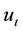is the instantaneous utility of consumption in period t. Following Köszegi and Rabin (2009) [6] , I assume the preference of the consumer as follows.

Assumption. The consumer has the reference-dependent preference on consumption. The instantaneous utility of consumption 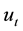consists of the following two terms

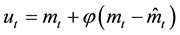(3)

where

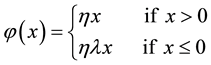(4)

The first term 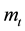is the utility directly coming from the consumption in period t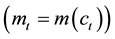. It is assumed that the consumption utility function is concave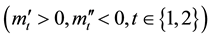. The second term is the gain-

oss utility from comparing with the reference level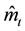. Note that denotes the weight of gain-loss utility, and the coefficient of loss aversion. This linear function is consistent with prospect theory (Kahneman and Tversky, 1979 [7] ) in that people tend to prefer avoiding losses than getting gains.

In period 0, the consumer evaluates the consumption of period 1 and period 2 equally, and makes the optimal allocation of consumption from the ex-ante perspective. However, this ex-ante optimal consumption allocation may not be preferred by self-1 because of present-biased preference. As the interest of this paper, we consider the time-consistent plans that will be implemented eventually, which is consistent with preferred personal equilibrium PPE by Köszegi and Rabin (2009) [6] .

3. Consumption Plans with Endogenous Labor Supply

3.1. Consumption and Working Behavior

For self-0, the optimal consumption level and labor supply which maximize the ex-ante utility are determined by

(5)

Note that.Because for the ex-ante optimal level we have, it makes the gain-loss utility parts in Equation (5) vanish. Since, self-0 prefers allocating income equally between period 1 and 2. However, the present-biased preference causes the consumer to over-consume, and in order to provide more resources she has to work longer. To answer 1) whether the ex-ante optimal consumption level and labor supply are the PPE solution; and 2) what the PPE consumption plans are while labor supply is endogenously determined, the following parts investigate whether there is incentive for the consumer to deviate from the ex-ante optimal levels.

For a consumption plan, the utility of self-1 when 1 & is

(6)

where is the reference level in the gain-loss utility. If the consumption plan in period 0 is &, then we have

(7)

There could be four scenarios where period-1 consumption and labor supply deviate from the ex-ante optimal level (&;&;&;&). It is can be shown that among those only the scenario & is possible for the consumer to choose¹. In other words, neither will the period-1 consumption decrease from the ex-ante optimal level, nor will the period-2 consumption increase.

When &, we take derivatives of with respect to and to investigate whether self- would like to deviate from the ex-ante optimal level by increase period-1 consumption or labor supply:

(8)

. (9)

In the neighborhood of the ex-ante optimal level, we have

(10)

(11)

Since and, the following lemmas could be obtained.

Lemma 1. In the case of &, when, the consumer in period 1 wants to increase from the ex-ante optimal level ; when, the consumer in period 1 does not want to increase from the ex-ante optimal level .

Self-0 prefers a smooth allocation. But when period 1 comes, the present-biased preference causes the consumer’s minds to change. When, self-1 would like to accept the smooth consump-

tion plan because her loss aversion is strong. However, when, the present-biased preference is so strong that she would not accept the smooth consumption level even though her consumption utility is reference-dependent.

Lemma 2. In the case of &, when, the consumer in period 1 wants to increase l from the ex-ante optimal level ; when, the consumer in period 1 does not want to increase l from the ex-ante optimal level .

The consumer with present-biased preference has to work longer to get higher income. Working longer leads to higher income level for the whole life, but also higher immediate disutility. When, self-1 would like to increase labor supply to get higher income. But when present bias becomes stronger, she is reluctant to work longer any more.

3.2. PPE Consumption Plans

In period 1, the present-biased preference causes the consumer to confront with two self-control problems: (1) how to allocate income; and (2) whether to work longer. Note that we consider endogenous labor supply, so consumption level and labor supply are simultaneously determined. Therefore, we have to jointly consider Lemma 1 and Lemma 2.

When, the increase of consumption from plan makes the gain-loss utility included, while no deviation of labor supply makes the first-order condition associating with labor in period 0 remained. Hence,

and jointly determine the consumption level and labor supply which are optimal

for the consumer in period 1. If the consumer in period 0 adopts it as the consumption plan, it will be implemented eventually, referred as the PPE consumption plan. With the same method, the other PPE consumption

plans under each condition (and) could be derived. To summarize, the following proposition is obtained.

Proposition 1.

(1) when, the PPE consumption plan is given by

&

(2) when, the PPE consumption plan is given by

&

(3) when, the PPE consumption plan is given by

&

Remark 1. In this model with endogenous labor supply and reference-dependent preference, the ex-ante optimal level is not included as a PPE consumption plan.

Associating with different levels of present-bias discount factor, the consumer exhibits different behavior by including corresponding first-order conditions. However, notice that for all the cases we have, , and.

To investigate whether these could mitigate the two self-control problems, consider the case without reference-dependent consumption utility. In the case without gain-loss utility, the first-order conditions in period 1 read

. (12)

Compare Equation (12) with the first-order conditions in Proposition 1, and since &, it could be found that all the PPE consumption plans help weaken the present-bias effect caused by quasi-hyperbolic discounting. Denote the consumption level and labor supply determined by first-order conditions in Equation (12) as (,) and, the following proposition is concluded.

Proposition 2. For all the PPE consumption plans, consumption level and labor supply satisfies that &.

By taking derivatives of first-order conditions under each case of, the following conclusions are obtained.

Proposition 3. For the PPE consumption plans, consumption level (,) and labor supply (l) have the properties as follows:

(1) when, , and;

(2) when, , and;

(3) when, , and.

According to Proposition 3, it is easy to show that for all PPE consumption plans, there exists a minimum value for period-1 consumption and labor supply when. This minimum value is determined by the first-order conditions:

. (13)

Under the conditions of Equation (13), the consumption and labor supply are the closest to the ex-ante optimal level. And when, it reduces to the first-order conditions of period 0.

4. Conclusion

This paper incorporates endogenous labor supply into the model of reference-dependent consumption, and derives the consumption level and labor supply in the preferred personal equilibrium. It is shown that the PPE consumption plans can attenuate the double self-control problems caused by present-biased preference. The smooth consumption pattern which is optimal for the ex-ante utility is not a time-consistent plan.

Acknowledgements

The author acknowledges the financial support from Research Subsidy of Kanazawa Seiryo University.

Cite this paper

LinZhang, (2015) Reference-Dependent Consumption with Endogenous Labor Supply. Theoretical Economics Letters,05,503-508. doi: 10.4236/tel.2015.54059

References

Appendix

When &, the life-time utility in period 1 reads

(A1)

Taking derivatives of with respect to and in the neighborhood of (,) leads to

(A2)

(A3)

Equations (A2) and (A3) imply that a decrease in or an increase in causes to decrease. Hence this scenario is excluded from the consumption plans. With the same method applied to the other two scenarios & and &, they are both excluded.

NOTES

¹See the Appendix for the other three scenarios.