Received 10 February 2015; accepted 22 March 2015; published 31 March 2015

ABSTRACT

In the paper, we investigate the pricing behavior of a risk averse monopoly. Since the focus is on the risk averse attitude of the firm, we ignore cost in our model. Demand is considered to be stochastic demand: as price decreases, the expected number of customers increases, but it has a varia- tion. Although demand is uncertain, it relates to the aggregation method of individual demands and the individual demand has the usual form. In our framework a risk neutral (or profit maximizer) monopoly does not change the product’s price as the number of clients increases. On product markets the risk averse monopoly with DARA utility function always increases the price as the number of clients grows, but in insurance markets the implication can be the opposite: the price of insurance may decrease as the number of clients increases.

Keywords:

Monopoly, Risk Aversion, Insurance, Market Size

1. Introduction

Stochastic demand is not unknown in the economic literature. In management science models it is well-studied (see e.g. [1] [2] ). In microeconomic models stochastic demand appears less frequently. If stochastic demand is considered in microeconomic models, it usually means that the demand depends on some unknown (external) parameter or it is due to some kind of bounded rationality. Barberá and Pattanaik [3] , for example, investigate the case where the decision maker chooses randomly between alternatives. In this paper, the individual demand has the usual form, but for a risk averse decision maker it is not appropriate to simply sum up the individual demands. As we will see, for a risk neutral firm summing up is acceptable, but for a risk averse decision maker the uncertainty about demand has a significant effect on the optimal price (see more on aggregation of stochastic in e.g. [4] [5] ).

It is usual in microeconomic theory that increased demand increases market price. We can think of Marshallian cross for instance. There are known exceptions, such as the Giffen goods. Hoy and Robson [6] gave an example where insurance can be a Giffen good. In our model the individual demand has a downward slope, therefore the case of Giffen good is excluded.

Pricing of a monopoly differs from pricing of a competitive firm. It can happen that a monopoly reduces its price due to the increased demand, but the decrease is related to the costs (natural monopoly for instance) or the increase of the demand is not uniform. In our model we would like to focus on risk aversion of the decision maker, thus we ignore costs. On the other side, the increase of demand is uniform.

We provide a simple framework for investigating the pricing of a risk averse monopoly. We distinguish between product market and insurance market. In the product market increased demand will cause increased monopoly price, but in the insurance market it can happen, that increased demand results in reduced price.

In the insurance economic literature there are usually two kinds of models: insurer has many (or many type of) contracts, but the insurer is risk neutral (e.g. [7] [8] ). In the other type of model the insurer is risk averse but the model investigates (one or few) typical contracts (e.g. [9] [10] ). It is very rare when a risk averse insurer is considered to have many insured, which is the everyday situation.

Insurance markets are dominated by a few (or not many) companies, which remind us to the market form of oligopoly. It depends on the situation whether the competitive economy or the monopoly is a more realistic mar- ket form. The presence of a monopolistic insurance company is accepted in the literature (see [7] ), which is also the case in our paper.

In Section 2, we present our theoretical model for both cases of product market and insurance market. In Section 3, we conclude the results.

2. Theoretical Model

In the model we consider a monopoly. It sells its product to (potential) customers. Cost is considered as sunk cost which does not affect the optimal price. The monopoly can fulfill the demand of arbitrary number of cus- tomers. An illustrative example is the case of a software vendor: the firm can sell any copies of a program with- out cost. Also an insurance company can supply insurance to many clients.

Customers can decide to buy the product or not, but they cannot buy fraction of the product. e.g. it is im- possible to buy a half of a software. In the insurance market it could be possible to buy fraction of the coverage, but we exclude this case. The clients’ decision is to buy full coverage or not to buy insurance. In the mo- nopolistic market the insurance company sets the contract’s properties and it is not interested in fractional cove- rages.

Each client has a reservation price (which differs from client to client), but the monopoly does not know the exact price, it knows only the distribution of the reservation prices within a greater community. So let 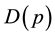be the probability that a (particular) client buys the monopoly’s product at price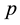. We assume that function 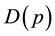is decreasing and it is continuously differentiable. If the monopoly has more than one potential client, say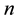, then the demand function will not be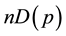, but the number of insureds follows a binomial dis- tribution. The probability that clients buy the product is:

where 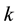can be any integer between 0 and.

The monopoly is risk averse and maximizes its expected utility. Its behavior can be described with a concave (risk averse) utility function.

2.1. Product Market

In case of a product market we can assume that, and for the simplicity we also assume that there ex- ists price 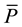such that.

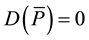The monopoly’s expected utility at price: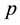

(1)

where 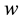denotes the monopoly’s initial wealth.

We assume that the expression has a unique maximum in and it is at least quasi-concave in. It is hard to give a condition for this property, but according to numerical verification it is not a strict assump- tion. If function has more than one local maximum then the theorems hold for local maxima.

If the monopoly is risk neutral (utility function is linear) then the expected utility becomes simple:. The monopoly’s optimal price does not depend on the market size.

In Theorem 1 we prove that a risk averse monopoly applies a lower price than a risk neutral monopoly.

Theorem 1. A risk averse monopoly sets a lower price than a risk neutral firm.

Proof. Let us see the expected utility’s (1) derivative with respect to price:

A risk neutral decision maker sets a price such that. So at

(2)

which is negative due to concavity of and negativity of. So, this completes the proof.

The interpretation of Theorem 1 is that a risk averse monopoly is satisfied with a lower price which ensures higher probability of selling.

What happens if the number of clients increases? The risk aversion solely is not enough to change the mo- nopoly’s price. Let us consider e.g. exponential utility function, , which is the case of constant absolute risk aversion (CARA). The closed formula for the expected utility is

(3)

The optimal price is the same for all.

If we assume decreasing absolute risk aversion (DARA), which is a more realistic assumption, we can state that the optimum price increases as market size increases:

Theorem 2. Let us consider a risk averse monopoly with a DARA (decreasing absolute risk averse) utility function. The monopoly determines a higher price in case of client, than in case of clients.

The proof can be found in the Appendix.

From Theorem 1 and Theorem 2 we can have the intuition that the optimal price converges to the risk neutral price as the number of clients tends to infinity. Unfortunately this intuition is false.

Example 1. Let, and, ,. Neither the optimal price for nor the optimal price for will depend on as can be seen from expression (3). According to Theorem 1 both of them is below the risk neutral price.

If we set then the optimal price will be somewhere between and. On the other hand, utility function is the sum of two utility functions with CARA property which have DARA property (see [11] ). If we have a utility function with DARA property, then according to Theorem 2 the optimal price will increase with market size, but it tends to have a lower value than the risk neutral price.

2.2. Insurance Market

In case of the product market there is only one source of uncertainty: whether the client buys the product or not. In case of insurance market there is another source of uncertainty: whether a claim occurs or not. For simplicity we investigate a two state model: a claim occurs with probability.

From classical risk theory we know that and (see [12] for instance).

The expected utility of an insurance company:

(4)

The expected utility becomes simple for a risk neutral monopoly again:. The optimal price does not depend on the market size (on parameter).

For an exponential utility function, there is a closed formula for the expected utility:

The optimal price for an exponential utility function does not depend on market size.

The risk averse insurance monopoly takes two impacts. It would set a lower price than a risk neutral company to sell more contracts as in the case of a product market. On the other hand, we also know from the classical risk theory that a risk averse firm applies higher price for insurance than a risk neutral. So there are two opposite effects, we could not decide on whether the price will be higher or lower than the risk neutral price (we can give ex- ample for higher and lower prices as well).

From risk theory we know that the average claim amount disperses less for a greater risk community, al- though greater extreme losses can also happen. A greater risk community can be advantageous for a risk averse decision maker, and as market size increases this advantage may exceed the profit loss from a lower price. In Example 2, we demonstrate the previously described situation: the insurance company can decrease its in- surance’s price as the demand (number of clients) increases. It is an interesting situation: the increase of market size is a common interest for insurance company and insureds. In product market the interest of the monopoly and the clients are always in conflict.

Example 2. Let,. It is a concave utility function with DARA property. Using this utility function there is a closed formula for the expected utility:

(5)

As we can see, the utility function is a mixture of a risk neutral part () and an ex- ponential part (the remaining part). The optimal (common) price has to be between the risk neutral price and

the price for exponential utility function (CARA price hereafter). If

then as n grows, the common price will be closer to CARA price, if, then the exponential part diminishes and the common price will be closer and closer to the risk neutral price.

Let parameter q and K take values such that and.

For the second condition it is enough if, which means that the risk neutral price is favor- able for a decision maker with exponential utility function. Now the common price is higher than the risk neutral price and lower than CARA price so the common price is also favorable for CARA deci- sion maker; as grows, the exponential part diminishes and the common price gets closer and closer to risk neutral price, so.

For numerical check: let. The risk neutral price is. Let,

and. The indifference price for CARA utility function is. It can be easily verified that the CARA price is higher than the risk neutral price. All the conditions hold. We set for a more illustrative example. Table 1 shows the optimal prices.

We can make two important remarks: let parameter be increased to 10. Now the risk neutral price is not favorable for a CARA utility function, but common price can still be favorable. If it is so then optimal price will decrease, but will tend to a higher value than the risk neutral price (see Table 1).

Let parameter be increased even more, so the common price will not be favorable for a decision maker with exponential utility function, so the exponential part does not diminish, the common price is increasing with the market size. For a more illustrative example, we set parameter to 100, so will be large enough for the demand. This is also a counter example for the intuition that the market price increases if it is lower than the risk neutral price and decreases if it is higher than the risk neutral price (see Table 1).

3. Conclusions

In the paper, we presented a microeconomic framework, in which a risk averse monopoly’s behavior can be investigated. We proved that in a product market a risk averse monopoly applies a lower price than a risk neutral (profit maximizer). If the risk aversion decreases with wealth (DARA), the market price will increase with the market size.

In the insurance market the price can decrease or increase with the market size even for utility function with DARA property. We have given numeric example for both cases.

Acknowledgements

I would like to thank Aegon Hungary insurance company, Insurance Education and Research Group, Corvinus University of Budapest (BOKCS) and Association of Hungarian Insurance Companies (MABISZ) for supporting my research. I thank Miklós Pintér, Péter Bíró, Bianka Ágoston and Tamás Polereczky for their suggestions and remarks. Naturally, all errors are mine.

References

Appendix

Proof of Theorem 2

Lemma 1. For monopoly’s expected utility the following recursive relationship holds:

(6)

Proof. We start from the recursive formula for binomial numbers: for all integers. Using this formula:

For the sake of simplicity we introduce the following notations:

And

It is easy to check that the recursive relationship (6) also holds for expressions and .

Lemma 2 is increasing.

Proof.

where is a positive term. For the determination of the sign of the second term we argue that

By the Cauchy’s mean value theorem there exist such that

Now one thing is missing: is decreasing. We know that positive linear combination

of utility functions with DARA property is also a utility function with DARA property (see [11] , page 104). If

we define, then for DARA property also holds, which

is equivalent to the decrease of.

Proof of Theorem 2. The first order condition of -client market:

Which can be rearranged as

(7)

We investigate the sign of at the optimal price of -client market. We can deter-

mine the sign of, if we determine the relationship of and

. Using (7) we need to decide the relationship between

and.

Using the recursive relationship (6):

Applying Lemma 2 and using some algebra we can state, that

Which actually means, that.