Received 10 October 2014; revised 5 November 2014; accepted 1 December 2014

ABSTRACT

Prospect theory believes that value judgments of decision-makers are associated with reference point. Based on this intuition, this paper analyzes the impacts of reference point as well as its change on individual value with two risk selection experiments, which are at the same wealth level but have different reference points. Experiments find that reference point has significant influences on value function and decision weight at the same wealth level. Moreover, via the value function diagram, we find that the value of a certain wealth level rising from a relatively low reference point is higher than the value of the same wealth level declining from a relatively high reference point which initially is raised from the lower reference one. Intuitively, it also explains that the changes of the reference point will lead to a decline in the overall value of decision-maker.

Keywords:

Prospect Theory, Reference Point, Value Function

1. Introduction

Compared with expected utility theory, prospect theory [1] , which is put forward by Kahneman and Tversky in 1979, does not focus on the concept of “rationality” [2] [3] , but pay more attentions to practical decision-making behaviors of decision-makers. Based on prospect theory, the behaviors of decision-makers have many characteristics, such as reference point, decision weight, loss aversion, which provide theoretical explanations for behaviors that deviating from the rational behaviors systemically. At present, there have been a lot literatures studying the actual behaviors of decision-makers. Tversky and Kahneman [4] introduced a cumulative function into the decision weight function and proposed cumulative prospect theory. Benartzi and Thaler [5] explained “equity premium puzzle” using prospect theory reference point and myopic loss aversion to simulate the value changes of decision-maker. Köszegi and Rabin [6] discussed the problem of psychological reference point selection, and proposed that the human psychological reference point was formed by a series of experience accumulated in the past, and could be inferred by using a general equilibrium model. Schmidt and Zank [7] described strong risk aversion and second-order stochastic dominance via cumulative prospect theory, and it was concluded that the strong risk aversion meant the decision weight function was convex on the gain domain and concave on the loss domain, but value function was not necessarily concave.

However, traditional methods which are used to elicit the utility function (such as utility equivalent method [8] , lottery equivalent method [9] , etc.) are not suitable to elicit the value function under prospect theory. Thus, Tversky and Kahneman [4] proposed a method to measure the parameters of value function under prospect theory, but its applicable scope was small. Then, Abdellaoui, Bleichrodt and Paraschiv [10] proposed their method without assuming any parameters. Their method could establish a direct relationship between decisions and value. However, because no parameters were assumed before the experiment, the method needed a large amount of experimental data, which made it less efficient. In order to minimize the amount of experimental data needed and improve the efficiency of their experiment, Abdellaoui, Bleichrodt and L’Haridon [11] put forward a parameter-hypothesized method, which suggested that the value function adopted the power specification. Using this method, Abdellaoui not only verified value function, decision weight, loss aversion and other relevant conclusions under prospect theory, but also firstly observed that value function was convex and risk aversion appeared at the same time due to the influences of the decision weight [11] . In addition, he found that loss aversion was more apparent on utility under risk than utility over time [12] . However, loss aversion coefficient measurement is controversial. Schmidt and Zank [7] pointed out that loss aversion coefficient could not be measured unless the power parameters in the gain and loss domain are equal.

We use the certainty equivalent method proposed by Abdellaoui et al. to design two risk selection experiments, in which 33 graduate students were employed from Huazhong University of Science and Technology as experimental subjects. The experiments describe the rough shape of the value function of subjects and try to reveal the influences of the reference point and its change at the same wealth level on individual value. It is essential to point out that this paper does not involve loss aversion coefficient measurement.

The paper proceeds as follows. Section 1 reviews previous empirical work on individual value under prospect theory. Section 2 describes our method for eliciting individual value. Section 3 describes the design of two experiments in which our method is applied. Section 4 describes the results of our experiment and Section 5 concludes.

2. Method

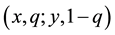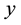This paper only involves binary prospects. All our results are valid under both prospect theory and cumulative prospect theory. Specifically, let denote the binary prospect that results in outcome with probability and in outcome with probability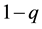. We select individual’s status quo before her or his decision-making as the reference point, and only consider the situation where the outcomes are both gains or both losses, so if outcomes are gains, then let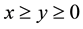, if outcomes are losses, then let.

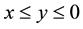The value of a prospect is evaluated mainly by three parts, namely the decision weight function 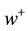on the gain domain, the decision weight function 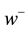on the loss domain, as well as the value function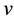. Under prospect theory, gain prospects are evaluated as, while loss prospects as.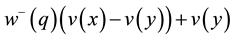

We adopt the following power specification as the value function on the gain or loss domain [11] :

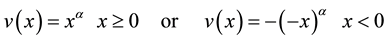
Specifically, x denotes the gain or loss of the decision-maker, 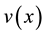denotes the value of the gain or loss, and denotes the power parameter of the value function. Here, the power specification is widely used to fit the value function. The value function is convex if or concave if on the gain domain, while the value function is concave if or convex if on the loss domain. Empirical studies showed that value function was concave on the gain domain [4] [13] , but results were not the same in the loss domain: most results showed a convex value function in the loss function [4] [14] , but there were still some experiments showing a concave value function [15] .

Based on the assumptions above, the decision weight of one probability on the gain domain, on the loss domain and the power parameter of the value function could be elicited as following. Here, is an objective probability.

On the gain domain, we firstly select an objective probability q, and then elicit equivalent value of the sub- jects, through a certain method. Specifically, G_i denotes the equivalent value of prospect, denotes the number of certainty equivalent questions. Abdellaoui, Bleichrodt and L’Haridon [11] have proved that the objective probability has nothing to do with characteristics of the value function.

From prospect theory model, we know

Namely

Due to, we know

Here, and can be obtained by the nonlinear least squares fitting. In addition, the method to obtain the parameters of the decision weight and the value function on the loss domain is similar to the method above.

Using the method above, we can analyze the impacts of reference point and its change at same wealth level. Specifically, we conduct K-S test on data of the related parameters within the interquartile range. -value is used to analyze whether the parameters of the subjects’ value function and decision weight change significantly. Specifically, we analyze the data within the interquartile range to eliminate the effects of extreme data in the experiments.

3. Experiment

We let subjects to answer questions independently. The whole experiment procedure included two experiments and several practice questions. And it would take about 30 minutes to complete. It is essential to point out that all money involved in this paper is RMB. The computer support system interface is shown in Figure 1.

3.1. Questions Design

Two experiments are designed. We can explore the impacts of reference point and its change at the same wealth level on the value function of decision-maker by the contrast of Experiment 1 and Experiment 2. In order to simplify the experimental analysis, we let. Experiment 1 and Experiment 2 are described below.

Before the start of Experiment 1, we gave subjects ¥0, and then asked them to answer seven certainty equivalent questions on the gain domain. Specific questions are shown in Table 1. The circumstance of Experiment 1 is consistent with the experiment conducted by Abdellaoui [11] .

At the end of Experiment 1, we asked subjects to evaluate their feelings with a positive evaluation scale which is shown in Figure 2. The evaluation question is shown as following.

Question 1: Before the start of the experiment, we have given you ¥0. If you can get ¥5000 now, how do you evaluate your feeling?

Before the start of Experiment 2, we gave subjects ¥10,000, and then asked them to answer seven certainty equivalent questions on the loss domain. Specific problems are shown in Table 1. Similarly, we asked subjects to evaluate their feelings with a negative evaluation scale which is shown in Figure 3 at the end of Experiment 2. The evaluation question is shown as following.

Question 2: Before the start of the experiment, we have given you ¥10,000. If you loss ¥5000 now, how do you evaluate your feeling?

We chose ¥5000 as gain or loss to make the evaluation score of subjects locate the middle of the scale as far as possible and to reduce the extreme evaluation score, thus uncovering positive the correlation between the evaluation score and the value of the subjects. We assumed that the value evaluation score is proportional to the value of the subject, and that positive evaluation scale or negative one is equal with the value of subject. Then we can obtain the rough shape of the value function of the subjects based on the median data of the power parameter of the value function and the average score of the value evaluation.

3.2. Procedure

Firstly, several practice questions were designed to help people be familiar with the experiment procedure. Here, the data of the practice questions would not be recorded. Practice questions contained two certainty equivalent questions on the gain domain and two on the loss domain. Each equivalent value was elicited by the binary iteration method [11] , and there are five iterations in total. In order to reduce the burden of the subjects, the system would round the outcomes down to multiples of 10.

After the practice phrase, Experiment 1 and Experiment 2 followed, and ten minutes were taken to complete each experiment respectively. All the questions in each experiment were conducted in random. To reduce the mutual influences between experiments, we gave ten minutes rest between two experiments. After each experiment, we selected two questions which were the third iteration of certainty equivalent questions in the gain or loss domain to analyze consistency of the subjects. Let denote the consistent proportion of the -th subject in the -th experiment. To test the overall reliability of subjects, wedefine the consistency index of the -th experiment

At the end of each experiment, the value evaluation question followed.

3.3. Incentive

All the subjects were required to play out one question with the actual payment divided by 1000, and the payments were settled in real-time.

Specifically, one question was selected by random after Experiment 1. For example, if a subject chooses the prospects in this question, then she or he could get by the probability and

by.

Before the start of Experiment 2, ¥10 was distributed to every subject. And we hinted them that ¥10 signified the initial reward ¥10,000, guiding subjects to choose state quo as their reference point. At the end of Experiment 2, one question was selected by random, and subjects were asked to pay with the actual loss divided by 1000.

4. Results

33 graduate students coming from Huazhong University of Science and Technology participated in the experiments, including 19 males and 14 females. According to the results of 33 subjects, the consistency of two experiments was 77% and 80% respectively. Because the stimulus value was generally close to the certainty equivalent in the third iteration, the reliability of the responses was good.

In this paper, if a subject had the same deviation in the two experiments, the change trend of median data and the data within interquartile range was not affected. Accordingly, we did not rule out any data of the subjects in the process of analysis. Individual estimation results are shown in Table 2, in which denotes the parameter of the value function on the gain domain, denotes the parameter of the value function on the loss domain.

Table 3 shows the median and interquartile range results of the parameters of the value function and the decision weight.

It can be seen from the median data in Table 3 that the value function of subjects was concave in Experiment 1 which regards ¥0 as the reference point, and also concave in Experiment 2 which regards ¥10,000 as the reference point. Moreover, the parameters of the decision weight of Experiment 1 and Experiment 2 were both less than 0.5 (0.48 and 0.43, respectively).

The significance of difference of the parameters within interquartile range was tested by K-S test. We found that p-values of the parameters of the value function and decision weight were less than 0.05 (as shown in Table 3). It showed that the value function and the decision weight were influenced significantly by the reference point and its change. As a result, the parameter of the value function increased while the decision weight decreased when the reference point changing from ¥0 to ¥10,000.

We counted the number of subjects according to score level of value evaluation questions, as shown in Figure 4.

It can be seen from Figure 4 that the average score of Experiment 1 was 5.09 while that of Experiment 2 was −6.52. According to our assumptions in this paper and the median of the parameter of the value function, when the wealth level was ¥5000, the ration between the value of Experiment 1 in which the wealth rose directly from ¥0 to ¥5000, and the value of Experiment 2 in which the wealth rose from ¥0 to ¥10,000, and then decreased from ¥10,000 to ¥5000, was 5.09:3.38. As a result, we could draw the value function diagram as shown in Figure 5.

We can see from Figure 5, when the reference point was ¥10,000, the value dropped to 0 while the wealth decreased down to ¥2938. While the wealth sequentially fell to ¥0, the value would drop to -5.18. In addition, the value of subject with the reference point of ¥0 was greater than that with the reference point of ¥10,000 except for the situation where the wealth level was close to ¥1000. More broadly, the value of subjects with reference point ¥0 was higher than that with reference point ¥10,000. It demonstrated that the value of the decision-maker was truly influenced by reference points and its changes. The value of a certain wealth level rising from the reference point ¥0 is higher than the value of the same wealth level decreasing from reference point ¥10,000, which is initially rising from the reference point ¥0. The results could intuitively explain that reference point’s continually changes result in a decline in the overall value of the decision maker in the process of multi-stage decision.

5. Conclusions

This paper designs two risk selection experiments with same wealth level which have different reference points,

and analyzes the impacts of reference point and its change on individual value. Afterwards, this paper also designs value evaluation questions to associate the value of the subjects with evaluation score, drawing the value function diagram of the subjects. The diagram shows that the value on the loss domain decreases much faster than the value on the gain domain with the same wealth, which is consistent with prospect theory. In addition, experiments find that reference point has substantial impacts on value function and decision weight at the same wealth level. Generally speaking, the value of a certain wealth level rising from a relatively low reference point is higher than the value of the same wealth level declining from a relatively high reference point which initially rising from the lower reference point.

Moreover, this paper intuitively explains that the changes of the position of the reference point can lead to a decline in the overall value of decision-maker through the analysis of value function diagram. And it can also serve as the explanation of “equity premium puzzle” from the experimental perspective.

Acknowledgements

This work was supported by National Natural Science Foundation of China 71071063 and 71471069.

References