Received 30 July 2014; revised 26 August 2014; accepted 25 September 2014

ABSTRACT

In this paper, a new model is proposed to empirically test the Capital Asset Pricing Theory. This model is based on the EGARCH-type volatilities in Nelson (1991) and the non-Normal errors of SSAEPD in Zhu and Zinde-Walsh (2009). Is the CAPM theory in Sharpe (1964), Lintner (1965) and Mossin (1966) still alive? Returns of Fama-French 25 stock portfolios (1926-2011) are analyzed. The Maximum Likelihood Estimation Method is used. Likelihood Ratio test (LR) and Kolmogorov-Smirnov test (KS) are used to do model diagnostics. Akaike Information Criterion (AIC) is used for model comparison. Simulation results show the MatLab program is valid. Empirical results show with non-Normal errors and the EGARCH-type volatilities, the CAPM theory is not alive. This new model can capture the skewness, fat-tailness, asymmetric effects and volatility persistence in the data. This new model has better in-sample fit than others. Portfolios with smaller size have larger Beta value.

Keywords:

Capital Asset Pricing Model (CAPM), Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD), EGARCH

1. Introduction

Capital Asset Pricing Model (CAPM) is first established by Sharpe (1964), Lintner (1965) and Mossin (1966) [1] , based on the investment portfolio theory of Markowitz (1959). The model measures the portfolio’s sensitivity to market risk, often represented by the quantity Beta (usually called coefficient), which is widely used in the financial industry. Since it offers a simpler approach to asset pricing and portfolio selection, it has been one of the most important benchmarks in modern finance theories. The theory of CAPM is usually expressed as following equation

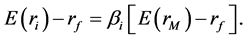(1)

That means, excess return of portfolio 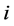has a linear relationship with market excess return [2] ¹. Since then, many theoretical and empirical researches about this model have been done.

However, some limitations of the CAPM theory are pointed out by some researchers such as Lucas (1978) [3] , Breeden (1979) [4] and Black (1976) [5] . One group of researchers try to revise and extend the CAPM from different theoretical aspects. For instance, Lucas (1978), Breeden (1979) and Shiller (1981) propose con- sumption CAPM (CCAPM). Wealth CAPM (WCAPM) is proposed by Black (1976), Lee (1986) and Gweon (1986). Another group of researches is to empirically test the CAPM theory with different methods or data. For instance, Fama and French (1993) [6] extend CAPM to a 3-factor model. For more applications or extensions about the CAPM theory, one can refer to Table 1.

To empirically test the CAPM theory, it is traditional to assume Normal error terms. However, Normal distri- bution can not capture the skewness, fat-tailness and asymmetric kurtosis of financial data. Thus, a plenty of researches have been done in order to extend the Normal. For instance, Subbotin (1923) [7] and Azzalini (1986) [8] designed the Exponential Power Distribution (EPD) and Skewed Exponential Power Distribution (SEPD), respectively. Zhu and Zinde-Walsh (2009) suggested the Asymmetric Exponential Power Distribution (AEPD), which can nest many distributions, such as Normal, Laplace, and so on. They demonstrate that the new models with non-Normal error distributions have many nice statistic properties. For researches that generalize Normal distribution, one can refer to Table 2.

Based on the SSAEPD in Zhu and Zinde-Walsh (2009) [9] and the EGARCH-type volatilities in Nelson (1991) [10] , in this paper, a new model is suggested and used to empirically test the CAPM theory. Different from the CAPM-GARCH models in Shen (2009) and Chen et al. (2012) [11] , in our new model, the error term is distributed as Standardized Standard AEPD (SSAEPD), which is more general than Normal Distribution. This new model may capture the skewness, fat tailness, leverage effects and volatility persistence better. The hy- potheses will be tested as follows:

1) With non-Normal error terms such as SSAEPD in Zhu and Zinde-Walsh (2009), and EGARCH-type volatilities in Nelson (1991), is the CAPM theory of Sharpe (1964), Lintner (1965) and Mossin (1966) still alive?

2) Can this new model beat the CAPM-SSAEPD model of Zhuo (2013) [12] ?

3) Can we find any new patterns for Fama-French 25 portfolios?

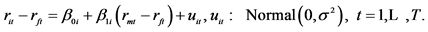(2)

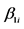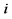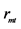If CAPM theory is alive, then the coefficient of should be statistically significant and the coefficient of is not statistically significant. is the rate of return for stock portfolio. is the rate of return for the risk-free asset. is the rate of return for the market. 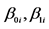are the coefficient parameters in the regression model. is the sample Size. The error term is distributed as Normal.

To answer these questions, simulation is done first. Then, the empirical data of Fama-French 25 stock port- folios are analyzed. Sample period is from January 1926 to December 2011. Method of Maximum Likelihood Estimation (MLE) is used to estimate parameters. Likelihood Ratio test (LR) is used for testing the significance of parameters. The Kolmogorov-Smirnov test (KS) is used to check the residuals. Akaike Information Criterion (AIC) is used for model comparison.

Simulation results show our MatLab program is valid. Empirical results show with non-Normal error terms and EGARCH-type volatilities, the CAPM theory of Sharpe (1964), Lintner (1965) and Mossin (1966) can not explain the US stock market. The estimates of this new model can capture fat-tailness, asymmetric effects, and volatility persistence in the data. The model with EGARCH-type volatilities and SSAEPD error terms has better in-sample fit than others by Akaike Information Criterion (AIC). A portfolio with a smaller Size may have a larger Beta value, which means that they can be more sensitive to the excess return over market.

Note: This table is a revision from Jin (2011).

The organization of this paper is as follows. The model and methodology are discussed in section 2. Simulation analysis is in section 3. Data and empirical results are reported in section 4. Section 5 is the conclusions and future extensions.

2. Model and Methodology

2.1. CAPM-SSAEPD-EGARCH

Based on the SSAEPD in Zhu and Zinde-Walsh (2009) and the EGARCH-type volatilities in Nelson (1991), in this paper, a new CAPM model is suggested (i.e., CAPM-SSAEPD-EGARCH). The CAPM-SSAEPD- EGARCH (m,s) model has following forms:

Notes: EPD = Exponential Power Distribution; SEPD = Skewed Exponential Power Distribution; AEPD = Asymmetric Exponential Power Distri- bution. This table is a revision from Jin (2011).

(3)

(4)

(5)

(6)

where are parameters to be estimated. is the rate of return for

stock portfolio. is the rate of return for the risk-free asset. is the rate of return for the market.

are the coefficient parameters in the regression model. is the sample Size. The error term is distributed as the Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD) proposed in Zhu and

Zinde-Walsh (2009). and are zero-mean I.I.D. sequences with continuous

distributions. is the conditional standard deviation.

If, , the model will be the EGARCH model of Nelson(1991). If

, the model reduces to CAPM-SSAEPD³ of Zhuo(2013). If

the model reduces to the CAPM-Normal,

which is usually used to test the CAPM theory. Different from the CAPM-SSAEPD-GARCH model of Lin (2013), EGARCH-type volatilities of Nelson (1991) is used to consider the leverage effects. If , then the model will be the CAPM-SSAEPD-EGARCH (1,1) with following math formula.

(7)

(8)

(9)

(10)

In this special case, the GARCH parameter measures the persistence in conditional volatility. If is relatively large, then the volatility will take a long time to disappear following a crisis or a shock in the market. The parameter measures the asymmetry or the leverage effect. If, then the model is symmetric. If, then the positive shocks generate less volatility than the negative ones. If, it suggests that positive shocks are more volatile than the negative ones. parameter is refered as the ARCH parameter, which represents the symmetric effect of the model.

2.2. Standardized Standard AEPD (SSAEPD)

The probability density function (PDF) of the SSAEPD⁴, proposed by Zhu and Zinde-Walsh (2009), is

(11)

where

(12)

(13)

(14)

(15)

(16)

(17)

(18)

And, , , ,. and are the parameters which control the left tails and right tails, respectively. Parameter controls the skewness of SSAEPD. When, SSAEPD will be reduced to standard Normal, i.e., Normal (0,1). The mean of is zero and its variance is 1.

2.3. Maximum Likelihood Estimation

In this paper, we estimate this new model with Maximum Likelihood Estimation (MLE). For simplicity, we define following notations and. The likelihood function is

(19)

where

(20)

(21)

(22)

3. Simulation Analysis

In this section, we simulate the data and derive the simulation results for the CAPM-SSAEPD-EGARCH (1,1).

(23)

(24)

(25)

(26)

The true parameters chosen are , ,

The data generation process (DGP) has following steps.

1) Given, we can generate SSAEPD random number⁵ series.

2) Set initial value, , and given , we can get and

.

(27)

3) Get and by following formulas

(28)

4) Generate random number series from Uniform (0,1). Given parameter, we can

get.

(29)

After we have the simulated data, we can use the simulated data to estimate the parameters in the

new model. The simulation results are reported in Table 3. The estimates from MatLab program are

,

, which are very close to the true values. For robustness exam, we also change the true parameters and re-run the simulation. We find out all the simulation results show the estimates are very close to the true parameters. Hence, we conclude the MatLab program is valid and can be applied to analyze empirical data.

Notes: T means the true parameters. E means the estimated parameters. R means the relative errors.

4. Empirical Analysis

4.1. Data

The 25 portfolio returns used in Fama and French(1993) are analyzed. Data are downloaded from the French’s Data Library⁶. Sample period is from January 1926 to December 2011. Caculated by Eviews, Table 4 lists the descriptive statistics of the 25 porfolios’ excess returns⁷. We can see that 23 out of 25 portfolios have positive values for the skewness, and all values of the kurtosis are more than, which documents asymmetric and fat tail characteristics. And the P-value of the Jarque-Bera test for each stock is zero. Hence, we conclude that all asset returns do not follow the Normal distribution under 5% significance level.

4.2. Estimation Results

4.2.1. CAPM Not Alive

· Estimates and Significant Tests for Parameter Restrictions

The estimates for the new model are listed in Table 5. Empirical results show the new model can capture the fat tailness⁸. Parameters in non-Normal error such as SSAEPD do not capture the skewness and the asymmetric tails⁹. In contrast, EGARCH-type volatilities could capture the asymmetric effects in the data. Hence, one can conclude that the EGARCH-type volatilities is more powerful to capture the asymmetric effect than non-Normal error such as SSAEPD.

For comparison, we also estimate the CAPM-EGARCH (1,1) model. The results are listed in Table 6 and Table 7. The sensitivity and volatility persistence in these models are not affected by different error

Note: ^*means the parameter is statistically significant under 5% significant level.

assumptions1⁰. However, the values of asymmetric parameter changes a lot¹¹.

Joint significance tests show both regression parameters are statistically significant (see Panel A of Table 8)¹². Individual significance tests show all coefficient is statistically significant. That is, market returns have significant effect on the returns of individual portfolio. 13 out of the 25 portfolios have statistically significant coefficient under 5% significance level¹³. And most of them concentrate in higher Book-to-market quintiles

Notes: P₁ = P₂ = 2.

Note: ^*means the parameter is statistically significant under 5% significant level.

or smaller Size quintiles. In conclusion, with non-Normal error distribution and EGARCH-type volatilities, the CAPM theory is not alive since they can earn Alpha returns.

12 out of 25 portfolios have significant parameter. The asymmetric parameters are most negative which means positive shocks generate less volatility than negative ones. All values of the ARCH terms and the GARCH parameters are statistically significant. The ARCH terms are relatively larger than 0.1, which means the volatility is sensitive to market shocks. The GARCH parameters are all positive and relatively large, e.g. above 0.9, so the volatility takes a long time to die out following a crisis or a shock in the U.S. stock market.

· Residual Checks

Test results for residuals (see Table 9) show that the error terms of these 25 stocks do follow SSAEPD¹⁴ and the CAPM-SSAEPD-EGARCH model is adequate for data used in Fama and French(1993). However, the CAPM-EGARCH model is not adequate for the data since most of its residuals do not follow the Normal distribution under 5% significance level¹⁵. Also, non-Normality¹⁶ is documented in Panel B of Table 8.

Same conclusions are also can be drawn from the PDFs of the residuals (i.e. method of “eye-rolling”). Taking one portfolio (Size quintile 2 and BE/ME quintile Low) as an example, we plot the residuals of CAPM- SSAEPD-EGARCH and CAPM-EGARCH in Matlab. They are shown in Figure 1 and Figure 2 respectively. In the figures, for the CAPM-SSAEPD-EGARCH, the difference between the PDF of the residuals and that of SSAEPD is smaller, and these curves are very close to each other. Therefore, one can conclude that the CAPM- SSAEPD-EGARCH fits the data well.

4.2.2. Higher Beta Values for Smaller Size Portfolios

The Beta value in the regression model stands for the relationship between the market portfolio and stock portfolio. The bigger the value, more volatile the fluctuation. From each column of the estimates of in the CAPM-SSAEPD-EGARCH model (see Table 5), we can find that the value decreases as the Size of the

Note: ^*means the null is rejected under 5% significant level.

portfolio gets bigger. Hence, one can draw a conclusion that a portfolio with a smaller Size may have a larger, which means that they are more sensitive to market. Same results can be drawn for CAPM-EGARCH model.

Then we compare the Beta values with those results in model CAPM-SSAEPD (see Appendix 1). From Table 10, we can see that 17 out of the 25 portfolios, marked with #, in the CAPM-SSAEPD-EGARCH model have smaller. These portfolios concentrate in the quintiles of smaller Size and higher Book-to-market. Hence, we conclude the portfolios with smaller Size and higher Book-to-market are less sensitive to market in the new model.

4.3. Model Comparisons

The new model is compared with others by AIC criterion (see Table 11). We find out our new model is the best one since its AIC are the smallest for 24 portfolios. Hence, we conclude the CAPM model with SSAEPD errors and EGARCH-type volatilities has better in-sample fit.

5. Conclusions and Future Extensions

Based on the SSAEPD in Zhu and Zinde-Walsh (2009) and the EGARCH-type volatilities in Nelson (1991), a

Note: ^# are marked with in CAPM-SSAEPD-EGARCH which are smaller than those in CAPM-SSAEPD.

Note: ^# marks the smallest AIC values.

new CAPM model is suggested in this paper (denoted as CAPM-SSAEPD-EGARCH). And this new model is used to empirically test the CAPM theory with 25 stock portfolios of Fama and French (1993). The sample period is from January 1926 to December 2011. Maximum Likelihood Estimation method is used. Likelihood Ratio test (LR) is used for testing the significance of the coefficients. The Kolmogorov-Smirnov test (KS) is used to check the residuals. Model is compared by the value of Akaike Information Criterion (AIC).

Our empirical results shows 1) With non-Normal error terms and EGARCH-type volatilities, the CAPM theory of Sharpe (1964), Lintner (1965) and Mossin (1966) can not explain the US stock market well. They can earn Alpha returns; 2) The estimates of SSAEPD-EGARCH parameters can capture fat-tailness, asymmetric effects and volatility persistence in the data. The EGARCH-type volatilities is more powerful to capture asymmetric effects than the parameters in SSAEPD; 3) The new model has better in-sample fit than others by Akaike Information Criterion (AIC); 4) A portfolio with a smaller Size value may have a larger Beta value, which means that they can be more sensitive to the market.

Future extensions will include but not be limited to the followings. First, different data can be analyzed. Second, the new model can be compared with others such as ARIMA, ARCH and SETAR. Third, the EGARCH-type volatilities and SSAEPD errors can be used to extend Fama-French 3-factor model. Last, the new model can also be applied to risk management such as calculating Value-at-Risk.

Acknowledgements

We also want to thank participants in the conference organized by Risk Management Institute, National University of Singapore (16-17 July, 2010), the Singapore Economic Review Conference organized by Nanyang Technological University (4-6 August, 2011), the International Conference on Applied Business & Economics at Manhattan, NY, U.S.A. (2-4 October 2013), The 8th International Conference on Asian Financial Markets & Economic Development at Nagasaki University (7-8 December 2013), Japan, the World Finance & Banking Symposium at Beijin, P.R.China (16-17 December 2013), the China Finance Reiview International Conference organized by Shanghai Jiaotong University (26-27 July., 2014), and the Canadian International Conference of Social Science and Education (CISSE, 10th & 11th March, 2014) organized by Ryerson University, Toronto, Ontario, Canada. The support of Xuefeng Li, Pin You, Mengyang Lin, Yimeng Hao and Yanjia Yang is gratefully acknowledged. The authors are responsible for all errors.

References

Appendix 1. Estimates from the CAPM-SSAEPD model

A new way to empirically test the CAPM theory using SSAEPD errors is suggestedy b Zhuo (2013) as follows:

(30)

(31)

where is the returns for the stock portfolio. is the returns for the market. is the risk-free rate., and are the coefficient parameters in the regression model. is the sample Size. The error term is distributed as the Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD) proposed by Zhu and Zinde-Walsh (2009).

The estimation results of CAPM-SSAEPD based on 25 portfolio returns used in Fama and French (1993) are listed in Table 12. According to the results, the skewness parameter of 23 portfolios are not equal to 0.5, which captures the skewness in the data. The left tail parameter and the right tail parameter of all the 25 portfolios are both smaller than 2, which documents the fat-tail characteristics. And 24 out of the 25 portfolios have fatter right tails than left tails. Hence, CAPM-SSAEPD can document the asymmetric tails.

NOTES

¹This equation is from page 301 of Bodie, Kane and Marcus (2006). For more reference about CAPM theory, please refer to Investments written by Bodie, Kane and Marcus (2006). To check the CAPM theory, researchers usually use following CAPM-Normal model to test the significance of parameters: and.

²Also see Theodossiou (2000) and Komunjer (2007).

³See Appendix 1.

⁴If is distributed as AEPD, denote it as If is distributed as standard AEPD, denote it as or If is distributed as standardized standard AEPD, denote it as or. The mean of is zero and the variance of is 1. That is,

⁵For the method to generate SSAEPD random variable, one can refer to Li, Tian and Zhen (2011).

⁶Thanks Din Yin who provides the well organized Excel files. Thanks Professor French for kindly providing the risk free rate by e-mail.

⁷Excess returns are got by portfolio returns minus the risk free rate.

⁸Since all values of are smaller than 2, which means fat tailedness is documented.

⁹Since most estimates of are equal to 0.5 and 14 out of 25 estimates of are equal to. For comparison, in Table 12, the estimates of CAPM-SSAEPD show that the skewness parameter of 23 portfolios is not equal to 0.5, which captures the skewness in the data. And 24 out of 25 portfolios have fatter right tails than left tails. Hence, CAPM-SSAEPD can document the asymmetric tails.

¹⁰In Table 7, 17 out of 25 stocks have the same estimates of Beta, and 20 estimates for of 25 portfolios are the same in both models.

¹¹In Table 7, 16 out of 25 stocks have different estimates of

¹²Likelihood Ratio test (LR) is used. The P-values of the joint significance test for all the 25 portfolios are close to 0, which means the coefficients of and are statistically significant under 5% significance level.

¹³The null hypothesis is in the CAPM-SSAEPD-GARCH model. The P-values of the LR test are listed in Panel B and Panel C of Table 8, respectively. Take one portfolio (Size quintile: Small; Book to Market quintile: 2) as an example, the P-value of its is 0, smaller than. That means, we can reject the null hypothesis and conclude that the coefficient has statistically significant effect on the value of portfolio returns. P-value of for this portfolio is 0. That means, under 5% significance level, we reject the null hypothesis and conclude that the coefficient is statistically significant. That is, market returns have significant effect on the returns of individual portfolio.

¹⁴The residuals for models are checked with Kolmogorov-Smirnov test. The null hypothesis of KS test is the residuals do follow some distribution. The P-value of KS test is in Table 9. If the P-value of KS test is bigger than, then do not reject the null hypothesis. Otherwise, reject the null hypothesis. First, apply KS test for the CAPM-SSAEPD-GARCH residuals with the null hypothesis

From the test results shown in Table 9, only 4 portfolios in CAPM-SSAEPD-EGARCH are not significant under 5% significant level, which suggests most error terms of 25 portfolios do follow SSAEPD.

¹⁵Then, we test the residual of CAPM-EGARCH, and the null hypothesis

Based on the test results shown in Table 9, we can see that 16 out of 25 portfolios in CAPM-EGARCH are not significant under 5% significant level, which suggests most of the error terms do not follow Normal distribution.

¹⁶We test the SSAEPD and EGARCH parameters respectively with Likelihood Ratio test. In Panel A of Table 6, all of the P-values except are statistically significant under 5% significance level. GARCH terms (see Panel F) and ARCH terms (see Panel H) are all statistically significant under 5% significance level. In Panel G, 12 out of the 25 portfolios have statistically significant leverage parameter. And most of these 12 portfolios concentrate in higher Book-to-market quintiles. That is, the asymmetric effects are more significant in stocks with higher Book-market quintiles. In Panel I, all of the P-values of portfolios are statistically significant under 5% significance level. The test results show strong non-Normality and EGARCH-type volatilities.