Theoretical Economics Letters
Vol.4 No.6(2014), Article
ID:46836,6
pages
DOI:10.4236/tel.2014.46054
The Equilibrium Allocation of Creative Capital to R&D in a Dynamic Creative Region
Amitrajeet A. Batabyal1, Hamid Beladi2
1Department of Economics, Rochester Institute of Technology, Rochester, USA
2Departmentof Economics, University of Texas, San Antonio, USA
Email: aabgsh@rit.edu, Hamid.Beladi@utsa.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 April 2014; revised 12 May 2014; accepted 3 June 2014
Abstract
In this note, we analyze a stylized creative region that is populated by members of the creative class. The representative individual in this region possesses a constant relative risk aversion (CRRA) utility function. The existing creative capital is used to produce a final consumption good and to conduct R&D. We first derive the equilibrium level of creative capital that is allocated to the R&D sector. Next, we show how this level is affected by changes in the parameters and in some of the model constants. Finally, we discuss the policy implications of our comparative statics results.
Keywords
Creative Capital, Creative Class, Dynamics, Economic Growth, R&D

1. Introduction
Since the publication of Richard Florida’s tome The Rise of the Creative Class in 2002, economists and regional scientists have attempted to comprehend the working of creative regions from a variety of perspectives. According to Florida [1] -[3] , creative regions are salient because they are the principal drivers of economic growth and development. In addition, creative regions are able to play this vital instrumental role because they are populated by members of the so called creative class who possess creative capital.
Florida ([1] , p. 8) defines the core of the creative class “to include people in science and engineering, architecture and design, education, arts, music and entertainment, whose economic function is to create new ideas, new technology and/or new creative content”. This creative class possesses creative capital which refers to “the intrinsically human ability to create new ideas, new technologies, new business models, new cultural forms, and whole new industries...” ([2] , p. 32).
Several researchers have now studied the ways in which the activities of the creative class have enhanced the growth prospects of a region. Markusen [4] concentrates on artists and criticizes the creative class notion. She points out that although artists make valuable contributions to the diversity and the vitality of cities, it is unlikely that they have much in common with other members of Florida’s creative class. In contrast, McGranahan and Wojan [5] focus on rural counties in the United States and note that their measure of the creative class is strongly associated with regional development. Donegan and Lowe [6] show that by deepening traditional labor market institutions and legislative supports, income inequality in cities with a large and creative talent pool can be ameliorated.
Lorenzen and Andersen [7] concentrate on 444 city regions in eight European countries and analyze the interplay between the older concept of “centrality” and the newer concept of the “creative class”. Their analysis demonstrates that the notion of centrality exerts a strong influence on what they call “urban hierarchies of creativity”. In turn, “the study of creative urban city hierarchies yields new insights into the problem of centrality” ([7] , p. 363). The statistical analysis conducted by Andersen et al. [8] shows that Florida’s creative class thesis is supported for larger Nordic cities but not as well for smaller Nordic cities. Challenging aspects of Florida’s creative class thesis, Comunian et al. [9] conduct an empirical analysis and note that it is certainly not obvious that bohemian graduates can be agents of knowledge spillovers. Olfert and Partridge [10] maintain that it would be misguided to set policy to increase the livability of a community by increasing its cultural footprint.
Very recently, a small number of theoretical studies of the functioning of creative regions have appeared in the literature. In this regard, Batabyal and Nijkamp [11] provide the first formal analysis of the creative capital accumulation decision faced by individuals in a creative region and then they compute the optimal length of time during which creative capital is accumulated. Batabyal and Nijkamp [12] analyze the effects of neutral and non-neutral productivity growth on creative capital in a trading regional economy. Finally, Batabyal and Nijkamp [13] study unbalanced growth in an urban economy that arises from the preferences of the creative class concerning the relative desirability of agricultural, manufacturing, and service goods.
The studies discussed in the preceding three paragraphs have advanced our understanding of aspects of the working of creative regions. Even so, there are virtually no theoretical studies of the equilibrium level of creative capital in the R&D sector of a creative region. Given this lacuna in the literature, we analyze the optimal allocation of creative capital to the R&D sector of a dynamic creative region. The remainder of this note is organized as follows. Section 2 adapts the prior work of Romer [14] and describes our theoretical model of a stylized creative region. Section 3 first derives the equilibrium level of creative capital that is allocated to the R&D sector. Next, it shows how this level is affected by changes in the parameters and in some of the model constants. Finally, it discusses the policy implications of the various comparative statics results. Section 4 concludes and then discusses potential extensions of the research delineated in this note.
2. The Theoretical Framework
Consider a stylized creative region that is populated by members of the creative class and that has an infinite horizon economy. The representative individual in the creative class displays constant relative risk aversion (CRRA) and this person’s CRRA utility function is denoted by
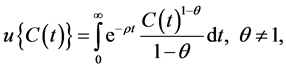 (1)
(1)
where 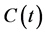 is consumption per creative class member at time
is consumption per creative class member at time 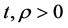 is the time discount rate, and
is the time discount rate, and 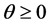 is the constant coefficient of relative risk aversion.
is the constant coefficient of relative risk aversion.
At any point in time in our creative region, there exists a range of ideas running from 0 to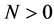 . Note that over time, the total number of ideas N is itself a function of time t. When an idea is available for use, the input into production that contains the idea can be produced using a technology that converts the creative capital one-for-one into the input. Let
. Note that over time, the total number of ideas N is itself a function of time t. When an idea is available for use, the input into production that contains the idea can be produced using a technology that converts the creative capital one-for-one into the input. Let 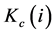 denote the quantity of creative capital devoted to producing input i and the quantity of input i that goes into the production of the single final good for consumption. We suppose that this final good is a knowledge good such as a smart phone or a laptop computer and that it is produced competitively with the production function
denote the quantity of creative capital devoted to producing input i and the quantity of input i that goes into the production of the single final good for consumption. We suppose that this final good is a knowledge good such as a smart phone or a laptop computer and that it is produced competitively with the production function
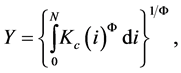 (2)
(2)
where 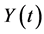 is output at time t and
is output at time t and 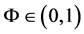 is a parameter of the production function. Let
is a parameter of the production function. Let  denote the total creative capital producing inputs in the final good sector and let the number of creative capital units producing each available input be the same. Then, for all i, we can write
denote the total creative capital producing inputs in the final good sector and let the number of creative capital units producing each available input be the same. Then, for all i, we can write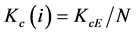 . Using this last expression and some algebra, we can rewrite the production function in Equation (2) as
. Using this last expression and some algebra, we can rewrite the production function in Equation (2) as
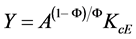 . (3)
. (3)
The return to creative capital at any time t is the wage which we denote by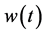 . In the remainder of this note, we normalize the price of the final consumption good to equal unity at all points in time.
. In the remainder of this note, we normalize the price of the final consumption good to equal unity at all points in time.
The sole right to use a given idea is held by a monopolist and we suppose that this monopolist is granted a perpetual patent on the exclusive use of this idea. Each patent holding monopolist first employs creative capital to produce the input associated with his idea and then he sells this input to producers of the final consumption good. Let 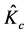 denote the total stock of creative capital in our creative region; we assume that this total stock does not grow over time. Then, equilibrium in the creative capital market at time t requires that
denote the total stock of creative capital in our creative region; we assume that this total stock does not grow over time. Then, equilibrium in the creative capital market at time t requires that
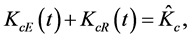 (4)
(4)
where 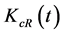 is the creative capital employed in the R&D sector at time t.
is the creative capital employed in the R&D sector at time t.
The production function for new ideas1 is linear in the creative capital employed in R&D or 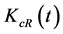 and proportional to the existing stock of knowledge
and proportional to the existing stock of knowledge . Mathematically, this function can be represented by the following differential equation
. Mathematically, this function can be represented by the following differential equation
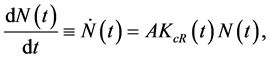 (5)
(5)
where the technology shifter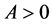 . There is free entry into the R&D sector in our creative region. The initial number of ideas
. There is free entry into the R&D sector in our creative region. The initial number of ideas 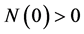 is supplied by monopolists. With this theoretical framework in place, our next task is to derive the equilibrium level of creative capital that is allocated to the R&D sector of the creative region under study.
is supplied by monopolists. With this theoretical framework in place, our next task is to derive the equilibrium level of creative capital that is allocated to the R&D sector of the creative region under study.
3. The Equilibrium Allocation of Creative Capital to R&D
We begin by maximizing the representative creative class member’s utility function given in Equation (1). This gives us the so called consumption Euler equation. Modifying equation 2.21 in Romer ([16] , p. 56), the Euler equation we seek is
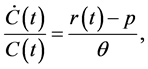 (6)
(6)
where 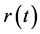 is the interest rate. Using Equation (6) to solve for the interest rate gives us
is the interest rate. Using Equation (6) to solve for the interest rate gives us
 (7)
(7)
The output of the final good is consumed in our creative region and all individuals comprising the creative class are essentially the same and hence they select the same time path of consumption. Therefore, equilibrium in the goods market requires that 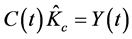 and this tells us that consumption grows at the same rate as output in our creative region. Now, adapting a condition in Romer ([16] , p. 129) to our problem, we infer that the rate of growth of output in our creative region is given by
and this tells us that consumption grows at the same rate as output in our creative region. Now, adapting a condition in Romer ([16] , p. 129) to our problem, we infer that the rate of growth of output in our creative region is given by 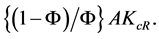 Using this last condition, we can re-write Equation (7) to give
Using this last condition, we can re-write Equation (7) to give
 (8)
(8)
Next, we focus on the profits earned from the discovery of a new idea at any time t. From equation 3.41 in Romer ([16] , p. 130), it follows that the present value of the profits earned by a monopolistic firm in the R&D sector from the discovery of a new idea at time t or 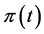 is
is
 (9)
(9)
Because there is free entry into the R&D sector of our creative region, anyone can hire 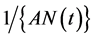 units of creative capital at the wage
units of creative capital at the wage 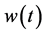 to produce a new idea. This tells us that the cost of coming up with a new idea is
to produce a new idea. This tells us that the cost of coming up with a new idea is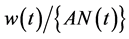 . Now, in equilibrium, the present value of the profits from a new idea must equal the cost of this idea. This means that
. Now, in equilibrium, the present value of the profits from a new idea must equal the cost of this idea. This means that
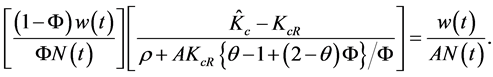 (10)
(10)
Solving Equation (10), we can find the optimal level of creative capital 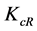 that is allocated to R&D in our creative region. This level is implicitly given by
that is allocated to R&D in our creative region. This level is implicitly given by
 (11)
(11)
Isolating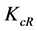 , Equation (11) can be simplified to
, Equation (11) can be simplified to . Solving this last expression for
. Solving this last expression for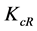 , we get
, we get
 (12)
(12)
Simplifying Equation (12) further gives us a compact expression for the equilibrium level of creative capital in the R&D sector or  The expression we seek is
The expression we seek is
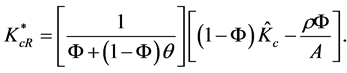 (13)
(13)
Clearly, this equilibrium allocation of creative capital must be non-negative. Therefore, using this fact, our final expression for the equilibrium level of creative capital in the R&D sector of our creative economy is given by
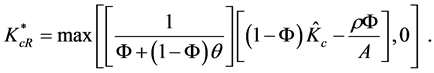 (14)
(14)
Inspecting Equations (13) and (14), we can determine the impact of changes in the various parameters and some of the model constants on the equilibrium level of creative capital 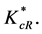 An increase in the constant stock of creative capital
An increase in the constant stock of creative capital 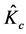 increases the ability of our creative region to produce new ideas. Similarly, an increase in the technology shifter A increases the rate at which new ideas arise in our creative region. Therefore, when either
increases the ability of our creative region to produce new ideas. Similarly, an increase in the technology shifter A increases the rate at which new ideas arise in our creative region. Therefore, when either  or A goes up,
or A goes up, 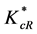 also goes up. This result means that regional authorities who are interested in increasing R&D activities in their region ought to put in place policies that, inter alia, encourage the entry of creative people into the region.
also goes up. This result means that regional authorities who are interested in increasing R&D activities in their region ought to put in place policies that, inter alia, encourage the entry of creative people into the region.
When the time discount rate ρ goes up, members of the creative class become more impatient, thereby privileging the present over the future. In this regard, it should be noted that more R&D now results in future payoffs and it is these future payoffs that are now less important to the creative class. Second, the discussion in Romer ([16] , pp. 50-51) tells us that the parameter θ reflects an individual’s willingness to shift consumption between different time periods. In particular, when θ rises, the elasticity of substitution between consumption at any two points in time falls, and this means that the representative creative class member is less willing to allow consumption to vary over time. This discussion about the effects of rising ρ and θ explains why 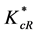 falls when either ρ or θ rises. The parameters ρ and θ are related to the preferences of the members of the creative class. As such, they generally cannot be directly influenced by regional policy. Even so, regional authorities who would like to increase R&D activities in their region ought to attempt to make members of the creative class more future oriented, possibly by encouraging long-term savings. This completes our discussion of the equilibrium allocation of creative capital to the R&D sector in a dynamic creative region.
falls when either ρ or θ rises. The parameters ρ and θ are related to the preferences of the members of the creative class. As such, they generally cannot be directly influenced by regional policy. Even so, regional authorities who would like to increase R&D activities in their region ought to attempt to make members of the creative class more future oriented, possibly by encouraging long-term savings. This completes our discussion of the equilibrium allocation of creative capital to the R&D sector in a dynamic creative region.
4. Conclusions
In this note, we analyzed a stylized creative region that was populated by members of the creative class. The representative individual in this region possessed a constant relative risk aversion (CRRA) utility function. The extant creative capital was used to produce a final consumption good and to conduct R&D. Our analysis led to three findings. First, we derived the equilibrium level of creative capital that was allocated to the R&D sector. Second, we showed how this level was affected by changes in the parameters and in some of the model constants. Finally, we discussed the policy implications of our comparative statics results.
The analysis in this note can be extended in a number of directions. One interesting extension would be to introduce uncertainty into the problem and then study the allocation problem of this note in a stochastic context. Second, it would be instructive to alter Equation (5) and examine the knowledge accumulation process when this process is subject either to negative externalities or to incomplete knowledge spillovers. Studies that incorporate these aspects of the problem into the analysis will increase our understanding of the ways in which the interactions between creative capital and innovative activities influence the growth and development of dynamic creative regions.
Acknowledgements
Batabyal acknowledges financial support from the Gosnell endowment at RIT and he thanks Cassandra Shellman for assistance in formatting the paper. The usual absolution applies.
References
- Florida, R. (2002) The Rise of the Creative Class. Basic Books, New York.
- Florida, R. (2005) The Flight of the Creative Class. Harper Collins Publishers, New York.
- Florida, R. (2005) Cities and the Creative Class. Routledge, New York.
- Markusen, A. (2006) Urban Development and the Politics of a Creative Class: Evidence from a Study of Artists. Environment and Planning A, 38, 1921-1940. http://dx.doi.org/10.1068/a38179
- McGranahan, D. and Wojan, T. (2007) Recasting the Creative Class to Examine Growth Processes in Rural and Urban counties. Regional Studies, 41, 197-216.
http://dx.doi.org/10.1080/00343400600928285 - Donegan, M. and Lowe, N. (2008) Inequality in the Creative City: Is There Still a Place for “Old-Fashioned” Institutions? Economic Development Quarterly, 22, 46-62.
http://dx.doi.org/10.1177/0891242407310722 - Lorenzen, M. and Andersen, K.V. (2009) Centrality and Creativity: Does Richard Florida’s Creative Class Offer New Insights into Urban Hierarchy? Economic Geography, 85, 363-390.
http://dx.doi.org/10.1111/j.1944-8287.2009.01044.x - Andersen, K.V., Hansen, H.K., Isaksen, A. and Raunio, M. (2010) Nordic City Regions in the Creative Class De-bate—Putting the Creative Class Thesis to a Test. Industry and Innovation, 17, 215-240.
- Comunian, R., Faggian, A. and Li, Q.C. (2010) Unrewarded Careers in the Creative Class: The Strange Case of Bohemian Graduates. Papers in Regional Science, 89, 389-410.
http://dx.doi.org/10.1111/j.1435-5957.2010.00281.x - Olfert, M.R. and Partridge, M. (2011) Creating the Cultural Community: Ethnic Diversity vs. Agglomeration. Spatial Economic Analysis, 6, 25-55.
http://dx.doi.org/10.1080/17421772.2010.540032 - Batabyal, A.A. and Nijkamp, P. (2010) Richard Florida’s Creative Capital in a Trading Regional Economy: A Theoretical Investigation. Annals of Regional Science, 44, 241-250.
http://dx.doi.org/10.1007/s00168-008-0262-7 - Batabyal, A.A. and Nijkamp, P. (2011) The Impact of Neutral and Non-Neutral Productivity Growth on Creative Capital in a Trading Regional Economy. Geographical Analysis, 43, 61-77.
http://dx.doi.org/10.1111/j.1538-4632.2010.00808.x - Batabyal, A.A. and Nijkamp, P. (2013) The Creative Class, Its Preferences, and Unbalanced Growth in an Urban Economy. Journal of Evolutionary Economics, 23, 189-209.
http://dx.doi.org/10.1007/s00191-012-0270-8 - Romer, P.M. (1990) Endogenous Technological Change. Journal of Political Economy, 98, S71-S102. http://dx.doi.org/10.1086/261725
- Acemoglu, D. (2009) Introduction to Modern Economic Growth. Princeton University Press, Princeton.
- Romer, D. (2012) Advanced Macroeconomics. 4th Edition, McGraw-Hill Irwin, New York.
NOTES

1This production function is also known as the innovation possibilities frontier. See Acemoglu (, p. 413) for additional details on this point.

