Theoretical Economics Letters
Vol.4 No.7(2014), Article ID:48555,6 pages
DOI:10.4236/tel.2014.47071
Asymmetric Impact of Informed Trading Activity on Stock Return Volatility
Alex YiHou Huang1,2, Ching-Liang Chang3
1Department of Information Management and Finance, National Chiao Tung University, Hsinchu City, Taiwan
2Innovation Center for Big Data and Digital Convergence, Yuan Ze University, Chung-Li City, Taiwan
3College of Management, Yuan Ze University, Chung-Li City, Taiwan
Email: ahuang1@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2014; revised 7 July 2014; accepted 3 August 2014
ABSTRACT
Prior research has shown that informed trading activity decreases the stock return volatility because trading causes stock prices to converge to fundamentals. On the contrary to existing studies, this paper documents the empirical asymmetric relation between informed trading activity and volatility. Stocks with relatively less private information are associated with lower participation of informed traders, and an increase in informed trading activity for those stocks would increase their return volatility. This finding is robust under both pooled and Fama-MacBeth regressions with various constructions for the realized volatility and probability of informed trading measurements.
Keywords: Stock Return Volatility, Informed Trading, Realized Volatility, PIN

1. Introduction
Volatility of financial assets is a key building block for studies in risk management, investment theory, and financial econometrics. A number of prior studies have shown that a significant amount of stock return volatility cannot be explained by changes in firm fundamentals (e.g., [1] ), raising the need for an additional explanation for volatility dynamics caused by stock trading behavior. For instance, several studies have documented the leverage effect in which volatility is negatively correlated with lagged returns (e.g., [2] [3] ), and Chordia et al. [4] demonstrated a significant degree of interaction between trading activity and stock returns at the intraday level. At daily frequency level, Avramov et al. [5] proposed a trading-based explanation for the leverage effect of volatility and showed that uninformed (i.e., liquidity-driven or herding) trades increase volatility following negative return shocks, while informed (i.e., contrarian) trades reduce volatility following positive shocks. This paper is motivated by the line of researches to investigate the relation between high frequent volatility and informed trading activity and, for the first time in literature, to document an asymmetric impact from trading behavior on realized volatility.
Previous investigations on the effect of informed trading activity on return volatility were inconclusive. Vega [6] found that informed traders are better able to extract more price-relevant private information from firm-specific characteristics. Foster and Viswanathan [7] , and Aslan et al. [8] showed that informed trading based on private information causes stock prices to converge to their fundamental values, thus reducing return volatility. This is consistent with the argument that uninformed traders with a greater dispersion of beliefs for new information tend to overreact to price movement, thus increasing volatility (e.g., [9] ).
On the other hand, Durnev et al. [10] argued that stocks with unavailable price-relevant information are generally traded based on public information, and thus their stock prices essentially signal fundamental values. Without private information, informed traders are inactive to trade such stocks. Kim and Verrecchia [11] demonstrated that skillful informed traders are able to detect arbitrage opportunities by analyzing public data. When informed traders exploit such information advantages, price movements tend to be more volatile.
This paper incorporates the above discussions and argues that informed trading activity should have an asymmetric impact on stock return volatility across stocks with different levels of private information. For stocks with relatively more price-relevant information, the participation of informed traders would bring the price closer to fundamental values thus reducing price volatility. For stocks with relatively less private information, informed traders only trade the stocks when they occasionally obtain unique information, which are often disagreed with public data. Consequently, the informed trading activity is likely driving prices away from the values inherited by the data and increases return volatility. This contention is formalized in following hypothesis:
Hypothesis: The impact from informed trading activity on stock return volatility differs across stocks with different levels of private information. For stocks with more (less) private information, one should observe 1) higher (lower) participation of informed trading and 2) lower (higher) volatility once more informed trading activity is detected.
This study applies the threshold regression model to investigate the asymmetric effect and employs the probability of informed trading (PIN) measurement of Easley et al. [12] to capture the level of the participation from informed traders. This paper finds that, for all sample stocks together, there is a negative relationship between informed trading activity and return volatility; this finding is consistent with one of Avramov et al. [5] . When differentiating stocks with high and low regimes of informed trading participation, this research shows that the negative relation only exists for stocks with higher PIN values. For stocks with low informed trading activity, an increase in PIN measurement would in fact lead to higher return volatility. This asymmetric relationship between informed trading and stock volatility provides important reference for research in investment theory and volatility dynamics.
The rest of the paper is organized as follows. Section 2 describes the data and methodology, while Section 3 presents and discusses empirical results. Section 4 concludes this research.
2. Data and Methodology
This study uses intraday data comprising the component stocks of the S&P500 index from 2006/1/1 to 2010/ 12/31. Component stocks that were removed from or added to the index during the sample period are both included. The S&P500 components were selected for the sample pool due to popularity of the index and high liquidity of the components. The five-year sample period covers key events such as the US housing bubble of 2006, the 2008 global financial crisis, and the 2009 American Recovery and Reinvestment Act. Since the empirical model is applied on a rolling basis over the sample period with in-sample windows from 120 to 210 trading days, stocks with data series shorter than 300 data points were omitted.
Stock prices and volumes were obtained from the CRSP database. To obtain the PIN measurement, both intraday trades and quote data were extracted from the TAQ database. Based on Easley et al. [12] , we measured the PIN by different in-sample lengths between 120 and 210 trading days. We proxy the stock return volatility using the realized volatility (RV) measurement based on Andersen et al. [13] . The RV is defined by summing the squares of intraday returns with estimation intervals of 3- to 15-minutes.
We first employ below pooled regression model to examine the overall relationship between return volatility and informed trading activity.
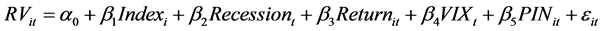 . (1)
. (1)
The RVit is the realized volatility for stock i on day t, the Indexi is the arithmetic average of the idiosyncratic volatility across sample period for stock i, Recessiont is a dummy variable equal to 1 (and 0 otherwise) if the data dates are part of a recessionary period defined by NBER, Returnit is the daily stock return, VIXt is the implied volatility index of the S&P500 at date t, and PINit is the PIN measurement for stock i on day t. The Indexi, Recessiont, and VIXt are included to respectively control for firm-specific systemic risk, macroeconomic conditions, and market-level volatility.
We then apply the following threshold regression model to investigate the asymmetric effect where Hansen’s [14] sequential estimation procedure is used for model estimation.
 (2)
(2)
The I(∙) is the indicator function, and l is the threshold inferred from the model. Since our data have both cross-sectional and time-series dimensions, we employ two alternative approaches to process the threshold regression. First, we use sequential procedure to obtain the threshold of each firm, and then pool the sample together to estimate Equation (2). Second, in the spirit of Fama-MacBeth method, we run the Equation (2) for each trading day, and then provide the statistics of estimated coefficients through the sample period.
In Equation (2), b4 and b5 respectively capture the impacts of PIN from highand low-regime cases. Stocks with PIN measurements generally higher than the threshold, meaning informed traders are more actively trading them. In this case, an increase to PINit is expected to reduce volatility because the participation of informed traders causes the price to converge to fundamental values, so b4 is expected to be negative. On the other hand, stocks with PIN measurements lower than the threshold involve less informed trading activity. According to the above discussion, an increase to PINit would likely exaggerate volatility, and b5 is expected to be positive.
3. Empirical Results
Table 1 presents summary statistics and correlation of variables. The mean (median) PIN is 0.194 (0.188), for which the shape of PIN is right skewed. Over our time interval, informed traders were more likely to buy, while uninformed traders were more likely to sell. This, too, causes the positive mean return of 0.07%. The realized volatility (RV) is highly correlated with PIN, PINH, PINL, Index, Spread, and Recession, but lightly correlated with Return. The correlations among independent variables are limited, so the issue of multicollinearity is relaxed. We will then be able to estimate our empirical model with reliable standard errors of coefficients.
Table 2 presents the empirical outcomes of pooled regression. There are 6 models in the table with the dependent variable, RV, produced by 3-minute interval and PIN measurements are estimated with 120 trading days. The 6 models are applied with different controlled variables across pooled and threshold regressions, and hence, they provide comprehensive investigation on the dynamic impacts on RV from PIN variables. Model 1 shows the results of Equation (1) with Index and Recession as controlled variables, and the estimate of the PIN coefficient is −33.52 and significantly away from zero. This shows that an increase in informed trading activity would reduce the stock return volatility on average, a result consistent with Avramov et al. [5] .
Model 2 provides the results of the threshold model based on Equation (2) using the same controlled variables as in model 1. The estimates of the PINH and PINL coefficients are −12.36 and 9.27, respectively and are both statistically significant. The outcomes show a negative correlation between RV and PIN for high-regime cases but a positive correlation for low-regime stocks. The results provide direct support for our hypothesis. Stocks with high-regime PIN measurements exhibit more activity by informed traders because they are associated with more private information. Consequently, the participation of informed traders brings the stock price back to fundamentals and reduces volatility. Stocks with a low-regime PIN have less private information available and are usually traded based on public data. When informed traders do have an information advantage on these stocks, their trading activity would then increase return volatility.
Models 3 and 4 use Return as the controlled variable to examine the relation of the realized volatility (RV) to PIN, PINH, and PINL. The estimate of the PIN coefficient in model 3 is −27.26, and the estimates of PINH and PINL in model 4 are −10.37 and 7.21, respectively. All estimates are statistically significant and consistent with
*This table presents the descriptive statistics and correlation of variables. See Section 2 for the definitions of variables.
Table 2. Pooled regression outcome.
*This table presents pool regression outcomes with the dependent variable as realized volatility based on a 3-minute interval. See Section 2 for descriptions of the data and the regression model. The t-statistics are shown in parentheses, and *** and ** respectively indicate the significance at the 1% and 5% level.
those in models 1 and 2. The asymmetric relation between RV and PIN is again confirmed where negative and positive coefficients are respectively observed for PINH and PINL. Models 5 and 6 use the VIX coefficient as the controlled variable. The estimate of the PIN coefficient in model 5 is −27.29, and the estimates of PINH and PINL in model 6 are −10.35 and 7.23, respectively. The results are again similar with those produced in previous models and supporting our hypothesis.
Table 3 provides the empirical outcomes of Fama-MacBeth regression using different constructions of the RV or PIN variables across models (with same set of controlled variables as Index and Spread). The variable of
*This table presents Fama-MacBeth regression outcomes. Models 1 and 2 have the dependent variable as realized volatility based on a 5-minute interval and PIN’s in-sample by 180 days. Models 3 and 4 have the dependent variable as realized volatility based on a 10-minute interval and PIN’s in-sample by 210 days. Models 5 and 6 have the dependent variable as realized volatility based on a 15-minute interval and PIN’s in-sample by 210 days. The t-statistics are shown in parentheses, and *** and ** respectively indicate the significance at the 1% and 5% level.
Spread is the bid-ask spread to control level of liquidity, and both Recession and VIX are market-level data and cannot be used under Fama-MacBeth framework. Please see table description for the in-sample construction details. Focusing on the estimates of the PIN coefficient in models 1, 3, and 5, we see that they are consistently negative and highly significant. For the PINH coefficient, the estimates are −32.49, −24.83, and −25.22 in models 2, 4, and 6, respectively. For the PINL coefficient, on the other hand, the estimates are 7.275, 4.736, and 3.088 in the same order. The results in Table 3 are highly consistent with those in Table2 We again observe the asymmetric effect between the RV and PIN variables regardless different in-sample structures. The outcomes of Table 3 confirm findings in Table 2; showing that more informed trading activity leads to lower return volatilities for stocks with high-regime PIN but higher volatilities for stocks with low-regime PIN. Compared to existing researches, the empirical application and outcomes of this study demonstrate that the asymmetric dynamics are better illustrated by the method of threshold model.
4. Concluding Remarks
The relationship between stock return volatility and informed trading activity is under exploration in financial research. Some prior studies show that informed trading reduces return volatility while others imply that, when informed traders trade against public data, their participation increases volatility. Using the threshold model, this study empirically finds an asymmetric relationship between informed trading and volatility. For stocks with more private information and higher participation of informed traders, the informed trading activity reduces volatility. Stocks with less private information are associated with lower participation of informed traders, and an occasional increase of informed trading activity would exaggerate return volatility. This novel finding clarifies the relationship between the two variables, and provides valuable insight for investment theory and volatility dynamics.
Acknowledgements
This research is supported in part by the National Science Council of Taiwan (NSC101-2410-H-155-028).
References
- French, K.R. and Roll, R. (1986) Stock Return Variances: The Arrival of Information and Reaction of Traders. Journal of Financial Economics, 17, 5-26. http://dx.doi.org/10.1016/0304-405X(86)90004-8
- Glosten, L.R., Jagannathan, R. and Runkle, D.E. (1993) On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. Journal of Finance, 48, 1779-1801. http://dx.doi.org/10.1111/j.1540-6261.1993.tb05128.x
- Huang, A.Y. (2011) Volatility Modeling by Asymmetrical Quadratic Effect with Diminishing Marginal Impact. Computational Economics, 37, 301-330. http://dx.doi.org/10.1007/s10614-011-9254-2
- Chordia, T., Roll, R. and Subrahmanyam, A. (2008) Liquidity and Market Efficiency. Journal of Financial Economics, 87, 249-268. http://dx.doi.org/10.1016/j.jfineco.2007.03.005
- Avramov, D., Chordia, T. and Goyal, A. (2006) The Impact of Trades on Daily Volatility. Review of Financial Studies, 19, 1241-1277. http://dx.doi.org/10.1093/rfs/hhj027
- Vega, C. (2006) Stock Price Reaction to Public and Private Information. Journal of Financial Economics, 82, 101-133. http://dx.doi.org/10.1016/j.jfineco.2005.07.011
-
Foster, F.D. and Viswanathan, S. (1994) Strategic Trading with Asymmetrically Informed
Traders and Long-Lived Information. Journal of Financial and Quantitative Analysis,
29, 499-518.
http://dx.doi.org/10.2307/2331107 -
Aslan, H., Easley, D., Hvidkjaer, S. and O’Hara, M. (2011) The Characteristics of
Informed Trading: Implications for Asset Pricing. Journal of Empirical Finance,
18, 782-801.
http://dx.doi.org/10.1016/j.jempfin.2011.08.001 - Fleming, M.J. and Remolona, E.M. (2002) Price Formation and Liquidity in the US Treasury Market: The Response to Public Information. Journal of Finance, 54, 1901-1915. http://dx.doi.org/10.1111/0022-1082.00172
-
Durnev, A., Morck, R. and Yeung, B. (2005) Value Enhancing Capital Budgeting and
Firm-Specific Stock Return Variation. Journal of Finance, 59, 65-105.
http://dx.doi.org/10.1111/j.1540-6261.2004.00627.x - Kim, O. and Verrecchia, R. (1997) Pre-Announcement and Event-Period Private Information. Journal of Accounting and Economics, 24, 395-419. http://dx.doi.org/10.1016/S0165-4101(98)00013-5
- Easley, D., Hvidkjaer, S. and O’Hara, M. (2002) Is Information Risk a Determinant of Asset Returns? Journal of Finance, 57, 2185-2221. http://dx.doi.org/10.1111/1540-6261.00493
-
Andersen, T.G., Bollerslev, T., Diebold, F.X. and Ebens, H. (2001) The Distribution
of Realized Stock Return Volatility. Journal of Financial Economics, 61, 43-76.
http://dx.doi.org/10.1016/S0304-405X(01)00055-1 -
Hansen, B.E. (2000) Sample Splitting and Threshold Estimation. Econometrica, 68,
575-603.
http://dx.doi.org/10.1111/1468-0262.00124


