Theoretical Economics Letters
Vol. 2 No. 5 (2012) , Article ID: 25617 , 5 pages DOI:10.4236/tel.2012.25084
Democratic, Plutocratic and Social Weights in Price Indexes*
Department of Economics, Centre for Research in Economics and Public Finance (CEFIP), University Roma Tre, Rome, Italy
Email: #paolo.liberati@uniroma3.it
Received April 27, 2012; revised May 28, 2012; accepted June 29, 2012
Keywords: Price Index; Distributional Characteristic; Social Weight; Inflation.
ABSTRACT
This paper introduces social considerations into the calculation of the price index. To this purpose, recourse is made to the concept of distributional characteristic. It is shown how an aggregate price index can be expressed as a weighted average of commodity-specific prices, with weights that depend on both the aggregate share of consumption and the way in which consumption is distributed across households. The proposed index provides a complementary basis for the analysis of the impact of inflation and for the calculation of its social value.
1. Introduction
In its most general form, an aggregate price index (CPI) can be calculated as a weighted average of commodity-specific price indexes. To this purpose, the most common alternatives are democratic and plutocratic weights. In the first case, households’ budget shares—i.e. the share of each good in total household’s budget—are simply averaged across households; in the second case, households’ budget shares are weighted by the share of consumption of every household over aggregate consumption. This paper proposes an alternative and complementary way to aggregate elementary price indexes, with weights that depend on both the level of consumption and the way in which consumption is distributed across households. This aim is achieved by allowing social weights to enter the weighting structure and to let the aggregate price index to depend on the distributional characteristic of the good (see [1-3]). Unlike the alternative structures, the resulting aggregate price index will react more to the prices of those goods that are consumed mainly by the poor. The paper is organised as follows. Section 2 deals with the definitions of the plutocratic and the democratic index. Section 3 introduces social weights into the weighting structure and defines the corresponding aggregate price index. Section 4 concludes.
2. Democratic and Plutocratic Weights
Aggregate consumer price indexes (CPI) can be defined as a weighted average of commodity-specific price indexes. The literature identifies two main weighting structures, which give rise to either the democratic or the plutocratic CPI, and that differ with respect to how they aggregate households’ budget shares
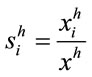
across households (where  is household’s h consumption of good i and
is household’s h consumption of good i and  is household’s h total consumption).
is household’s h total consumption).
The democratic method simply requires to average households’ budget shares. The commodity-specific weight is therefore given by:
 (1)
(1)
where the superscript D stands for “democratic”, H is the total number of households and . Using this weighting structure, the corresponding CPI will be given by:
. Using this weighting structure, the corresponding CPI will be given by:
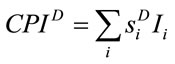 (2)
(2)
where 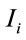 is the commodity-specific price index. Thus, in the democratic index, the price of each good is weighted by the average budget share of that good.
is the commodity-specific price index. Thus, in the democratic index, the price of each good is weighted by the average budget share of that good.
With the plutocratic method, instead, each household budget share is weighted by the share of total household expenditures 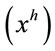 on aggregate expenditures X (where
on aggregate expenditures X (where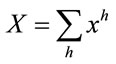 ). In symbols:
). In symbols:
 (3)
(3)
where the superscript P stands now for “plutocratic” and . Correspondingly, the aggregate plutocratic index will be given by:
. Correspondingly, the aggregate plutocratic index will be given by:
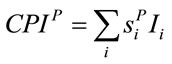 (4)
(4)
Thus, the value of the aggregate CPI can vary according to the method used. This has originated a wide literature on the plutocratic gap (the difference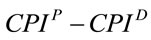 ) and on its empirical measurement ([4-6]); to this regard [5,6], for example, have derived a characterization of the CPI plutocratic gap in terms of dispersion of household’s expenditures and the sample covariance between the variation of budget shares and commodity-specific price indexes.
) and on its empirical measurement ([4-6]); to this regard [5,6], for example, have derived a characterization of the CPI plutocratic gap in terms of dispersion of household’s expenditures and the sample covariance between the variation of budget shares and commodity-specific price indexes.
3. The Social Value of the Price Index
3.1. Social Weights
To the purpose of explaining the meaning of the proposed index, it is worth conveniently rewriting Equation (3) as follows:
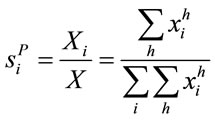 (5)
(5)
As it is clear from the numerator of Equation (5), the aggregation of consumption of good i across households implicitly gives the same weight to every household. In other words, in the plutocratic weight, it is not relevant whether the same level of 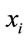 is consumed by a poorer or by a richer household. This means that two goods j and k whose consumption is differently distributed across households, but that have the same share on total consumption
is consumed by a poorer or by a richer household. This means that two goods j and k whose consumption is differently distributed across households, but that have the same share on total consumption
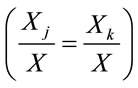 count the same in the calculation of the plutocratic index. Our proposed index tries to remove this feature by introducing distributional weights in Equation (5)1. In particular, consider a structure of household-specific distributional weights
count the same in the calculation of the plutocratic index. Our proposed index tries to remove this feature by introducing distributional weights in Equation (5)1. In particular, consider a structure of household-specific distributional weights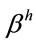 , possibly derived by an individualistic social welfare function2, with the only constraint that
, possibly derived by an individualistic social welfare function2, with the only constraint that 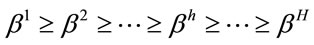 (i.e. distributional weights are non-increasing with income). Then, define:
(i.e. distributional weights are non-increasing with income). Then, define:
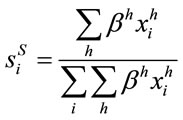 (6)
(6)
where 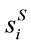 stands for social weight. As one can see, the social weight is a modified version of the plutocratic weight in (5), the modification being the inclusion of household-specific distributional weights that give more relevance to consumption of poorer households. For example, for a given level of
stands for social weight. As one can see, the social weight is a modified version of the plutocratic weight in (5), the modification being the inclusion of household-specific distributional weights that give more relevance to consumption of poorer households. For example, for a given level of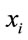 , if
, if ,
,  will count twice as much
will count twice as much 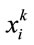 in the calculation of the social weight.
in the calculation of the social weight.
Now, recall the definition of the distributional characteristic given in [2], by which:
 (7)
(7)
where 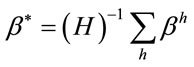 is the average distributional weight. The distributional characteristic (DC) is a welfare-based indicator of how consumption is distributed across households. The higher the value of
is the average distributional weight. The distributional characteristic (DC) is a welfare-based indicator of how consumption is distributed across households. The higher the value of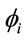 , the higher the concentration of consumption of good i among the poorest households. Note that if
, the higher the concentration of consumption of good i among the poorest households. Note that if ,
,  (i.e. distributional weights are the same for all households), then
(i.e. distributional weights are the same for all households), then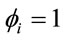 ,
, 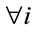 , which implies that the concept of distributional characteristic has a meaning only when consumption is differently weighted along the welfare ranking. Note also that the distributional characteristics are not necessarily correlated with households’ budget shares (see [3]). Intuitively, a good bought only by poor and not bought by non-poor may have a low budget share (if poor devote few resources to them) but a high distributional characteristic.
, which implies that the concept of distributional characteristic has a meaning only when consumption is differently weighted along the welfare ranking. Note also that the distributional characteristics are not necessarily correlated with households’ budget shares (see [3]). Intuitively, a good bought only by poor and not bought by non-poor may have a low budget share (if poor devote few resources to them) but a high distributional characteristic.
From (7), we know that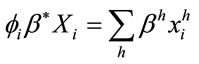 . Replacing this latter expression into (6) yields:
. Replacing this latter expression into (6) yields:
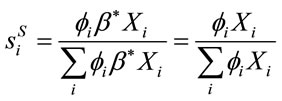 (8)
(8)
where it is clear that, analogously to the democratic and the plutocratic weighting structure,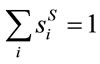 . By dividing the numerator and the denominator of the last term of Equation (8) by X (i.e., total consumption), one can have:
. By dividing the numerator and the denominator of the last term of Equation (8) by X (i.e., total consumption), one can have:
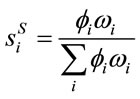 (9)
(9)
where
 .
.
The interpretation of Equation (9) is that when households are differently weighted along the income scale, the weights of commodity-specific price indexes will become a mixture of the aggregate share  and of the way in which consumption is distributed across households
and of the way in which consumption is distributed across households . Instead, when distributional weights are the same across households,
. Instead, when distributional weights are the same across households,  will collapse to
will collapse to , as
, as ,
, 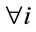 , and
, and  .
.
Thus, the social weight  will be low either when the share of good i is low (consumption of the good is not very important in the society) or when the distributional characteristic is low (the good is marginally consumed by poor), which both seem desirable properties of a social index. For example, if two goods r and t have the same aggregate share of five per cent of total consumption, but r is mostly consumed by the poor and t is mostly consumed by the rich, it will be that
will be low either when the share of good i is low (consumption of the good is not very important in the society) or when the distributional characteristic is low (the good is marginally consumed by poor), which both seem desirable properties of a social index. For example, if two goods r and t have the same aggregate share of five per cent of total consumption, but r is mostly consumed by the poor and t is mostly consumed by the rich, it will be that , and thus
, and thus  will count more than
will count more than  in a social perspective3. This implies that the social value of the price index of any commodity (or of a corresponding price change), other things being equal, will be higher when the poor spend a higher proportion of the total spending on that good (i.e., when
in a social perspective3. This implies that the social value of the price index of any commodity (or of a corresponding price change), other things being equal, will be higher when the poor spend a higher proportion of the total spending on that good (i.e., when  is greater) and not when expenditures on that good are a higher proportion of their own budget (see [3]). It follows from Equation (9) that:
is greater) and not when expenditures on that good are a higher proportion of their own budget (see [3]). It follows from Equation (9) that:
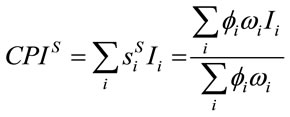 (10)
(10)
Expression (10) more clearly reveals that the social value of the price index of commodity i will be higher not only when expenditures on this commodity are a greater part of total spending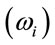 , but also when this commodity has a greater distributional characteristic
, but also when this commodity has a greater distributional characteristic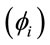 .
.
At this stage, a simple example may help clarify the mechanics of the proposed index and the differences with the standard democratic and plutocratic CPI. For convenience, and without loss of generality, the example is built by considering price changes (i.e., inflation) rather than the price index4. Table 1 is built considering two individuals (j and k) and two goods (A and B). Individual j, who is poorer, consumes a small fraction of A, which is 4.8 percent of its budget, while it consumes the whole amount of good B, which is 95.2 percent of its budget. Individual k, who is richer, spends 100 per cent of its budget on A. Table 1 reports the required variables to calculate the democratic and the plutocratic CPI. Assume that inflation on good A is 10 percent and inflation on good B is 20 per cent. Now, the democratic CPI can be calculated by weighting commodity-specific inflation rates by the average budget share of each commodity (the democratic weight in Table 1). This would yield 14.8 percent. The plutocratic CPI, instead, weights commodity-specific inflation rates by  (the plutocratic weight in Table 1), which would yield 14.3 percent. Note that the plutocratic CPI is lower as the good with the highest inflation (good B) is also the good with the lowest aggregate share (0.435 < 0.565 in the table).
(the plutocratic weight in Table 1), which would yield 14.3 percent. Note that the plutocratic CPI is lower as the good with the highest inflation (good B) is also the good with the lowest aggregate share (0.435 < 0.565 in the table).
Consider now the parameters required to calculate . Column (6) introduces the distributional weights 0.6 and 0.3, under the simple assumption that j has twice as much distributional weight than k. The average distributional weight is 0.45. Note that weights can be of any magnitude, with the only constraint that
. Column (6) introduces the distributional weights 0.6 and 0.3, under the simple assumption that j has twice as much distributional weight than k. The average distributional weight is 0.45. Note that weights can be of any magnitude, with the only constraint that . The distributional characteristic of good A is instead calculated as 0.692, while the same parameter for B is equal to 1.333. In this working example,
. The distributional characteristic of good A is instead calculated as 0.692, while the same parameter for B is equal to 1.333. In this working example, 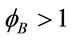 , as greater absolute amounts of good B are consumed by the poor individual. Thus, from a social perspective, inflation on good B should deserve more attention than inflation on good A. By applying Equation (9), social weights will be 0.403 for good A and 0.597 for good B.
, as greater absolute amounts of good B are consumed by the poor individual. Thus, from a social perspective, inflation on good B should deserve more attention than inflation on good A. By applying Equation (9), social weights will be 0.403 for good A and 0.597 for good B.
It is worth contrasting these values with the plutocratic weights. In this latter case, good A has a greater weight because its share on total consumption is greater. In the case of social weight, good A has still the greatest share on total consumption, but it is consumed more by the richest individual, which means that its distributional characteristic is lower. The combined weights reveal that good B is socially more relevant—aggregate consumption is lower but consumption is concentrated on poorer households. According to this line of reasoning, one can expect that since good B has also the highest inflation rate, the social price index should be higher than the plutocratic index. Indeed, the calculated social price index is 0.160, i.e., closer to the inflation rate of the good that is mostly consumed by the poorest individual. Thus, ceteris paribus,  reacts more to inflation rates that hit goods mainly consumed by poor (i.e., with a high distributional characteristic)5.
reacts more to inflation rates that hit goods mainly consumed by poor (i.e., with a high distributional characteristic)5.
The differences among the various types of price index may be best picked if one considers the behaviour of all indexes with respect to a change of a single price index

Table 1. A comparison between plutocratic, democratic and social weights.
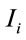 . In particular:
. In particular:
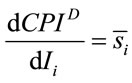 (11a)
(11a)
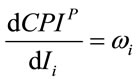 (11b)
(11b)
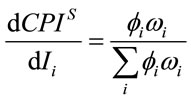 (11c)
(11c)
Equation (11a) tells that the reaction of the democratic CPI to a change in the price of good i is measured by the average budget share. This means that  will increase more if inflation falls on goods that count more in the households’ budget, regardless of whether they count more in the budget of poorer or richer households6. By Equation (11b), instead, one can infer that
will increase more if inflation falls on goods that count more in the households’ budget, regardless of whether they count more in the budget of poorer or richer households6. By Equation (11b), instead, one can infer that  will increase more when the price change falls on goods that are a large part of the aggregate total spending. Finally, Equation (11c) reveals that
will increase more when the price change falls on goods that are a large part of the aggregate total spending. Finally, Equation (11c) reveals that  is sensitive not only to the aggregate share of good i, but also to the way in which the consumption of this good is distributed across households.
is sensitive not only to the aggregate share of good i, but also to the way in which the consumption of this good is distributed across households.
3.2. Household-Specific Price Indexes
Finally, it is worth reconciling the use of aggregation schemes reported in (2), (4) and (10) with the household-specific indexes. For each household, all methods imply:
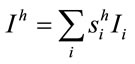 (12)
(12)
However, the methods differ in how they aggregate expression (12) across households. The democratic method leads to
 which gives the same result as Equation (2); the Plutocratic method leads to
which gives the same result as Equation (2); the Plutocratic method leads to
 which is equivalent to Equation (4); the social method leads to
which is equivalent to Equation (4); the social method leads to
 which is equivalent to Equation (10).
which is equivalent to Equation (10).
4. Conclusion
This paper has proposed a social price index to complement the information embodied in the already available democratic and plutocratic indexes. This index is based on the concept of distributional characteristic and is obtained as a natural extension of the plutocratic index. In particular, in the social index, commodity-specific price indexes are weighted by a composite factor, given by the product of the aggregate share of good i 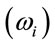 and of the way in which consumption is distributed across households
and of the way in which consumption is distributed across households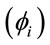 . As a consequence, the social price index collapses to the plutocratic index when all households are equally weighted along the income scale, i.e., when the distributional characteristics of the goods are all equal to one. This implies that the plutocratic index can be interpreted as a special case of a more general social index, the case being that of equal distributional weights for all households. We think that this index may have straightforward applications in the analysis of the impact of all price movements, including the assessment of the social value of indirect tax reforms.
. As a consequence, the social price index collapses to the plutocratic index when all households are equally weighted along the income scale, i.e., when the distributional characteristics of the goods are all equal to one. This implies that the plutocratic index can be interpreted as a special case of a more general social index, the case being that of equal distributional weights for all households. We think that this index may have straightforward applications in the analysis of the impact of all price movements, including the assessment of the social value of indirect tax reforms.
REFERENCES
- E. Ahmad and N. Stern, “The Theory of Reform and Indian Indirect Taxes,” Journal of Public Economics, Vol. 25, No. 3, 1984, pp. 259-298. 10.1016/0047-2727(84)90057-4
- M. S. Feldstein, “Distributional Equity and the Optimal Structure of Public Prices,” American Economic Review, Vol. 62, No. 1, 1972, pp. 32-36.
- F. Navajas and A. Porto, “Budget Shares, Distributional Characteristics and the Direction of Tax Reform,” Economics Letters, Vol. 45, No. 4, 1994, pp. 475-479. 10.1016/0165-1765(94)90090-6
- M. Kokoski, “Alternative Consumer Price Index Aggregations: Plutocratic and Democratic Approaches,” Office of Price and Living Conditions, Working Paper 370, 2003.
- E. Ley, “On Plutocratic and Democratic CPIs,” Economics Bulletin, Vol. 4, No. 3, 2002, pp. 1-5.
- E. Ley, “Whose Inflation? A Characterization of the CPI Plutocratic Gap,” Oxford Economic Papers, Vol. 57, No. 4, 2005, pp. 634-646. 10.1093/oep/gpi040
NOTES
*I wish to thank an anonymous referee, Marilena Barbieri, Antonio Scialà and Shlomo Yitzhaki for insightful comments on a previous version of this paper. Remaining errors are mine.
#Corresponding author.
1On the need of making explicit the value judgments on the income distribution involved in this kind of measurement, see also [6].
2In particular, one can define 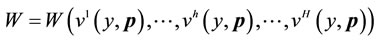 as an individualistic social welfare function that depends on individuals’ indirect utility functions defined on income y and prices p. In this framework, the distributional weight is best interpreted as
as an individualistic social welfare function that depends on individuals’ indirect utility functions defined on income y and prices p. In this framework, the distributional weight is best interpreted as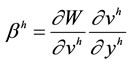 , i.e. as the social marginal utility of income.
, i.e. as the social marginal utility of income.
3As a real-life example one can take the case of bread (B) in Egypt, whose price is very low (as it is government-subsidised) and is consumed exclusively by the poor. At the same time, the price of lamb (L) is higher, but richer households consume more of this good. As a consequence, if the share of bread in total consumption is lower than the share of lamb, 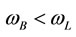 , but
, but , the social value of the corresponding prices will be the combination of a size and of a distribution effect of the consumption of the two goods, as expected by a social index.
, the social value of the corresponding prices will be the combination of a size and of a distribution effect of the consumption of the two goods, as expected by a social index.
4However, CPI notation is here left to denote inflation.
5In the case where inflation were 0.2 on good A and 0.1 on good B (not reported in table), the plutocratic index would be 0.157, while the social index would be 0.140, the explanation being that in this case the highest inflation would have hit the good that is mostly consumed by the richest individual. As a consequence, the social value of inflation would be lower.
6For example, assume that the average budget share of bread is 20 percent and bread counts more in the budget of poor households and also assume that the average budget share of luxury cars is 20 percent and luxury cars counts more in the budget of richer households. According to (14a),  will react in the same way to the same increase of price of both bread and luxury cars.
will react in the same way to the same increase of price of both bread and luxury cars.

