ABSTRACT

In this paper, we study the actual operating of an insurance company with random income. A double compound Poisson-Geometric risk model with interference was established. By using the martingale method, the adjustment coefficient equation, the formula and the upper bound of ruin probability, the time to reach a given level in this new risk model were obtained.

1. Introduction

As one of the most important topics in risk theory, the ruin problem in stochastic environments has been studied by many researchers [1,2]. In classical risk model, the claim number process was assumed to be a Poisson process and the individual claim amounts were described as independent and identically distributed random variables. In recent years, the classical risk process has been extended to more practical and real situations. For most of the investigations treated in risk theory, it is very significant to deal with the risks that rise from monetary inflation in the insurance and finance market, and also to consider the operation uncertainties in administration of financial capital.

In order to get more realistic models, the perturbed risk process was introduced by Dufresne and Gerber [3] and investigated by Veraverbeke [4]. The classical risk process perturbed by diffusion is given as follows:

where u is the initial surplus of an insurance company, c > 0 is the gross premium rate and

is the aggregate claim process. denotes a Poisson process with intensity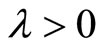; 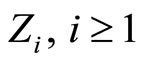is a sequence of independent and identically distributed (i.i.d. for short) nonnegative random variables, independent of . 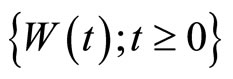is standard Brownian motion with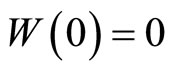. Based on the foregoing model, Dufresne and Gerber obtained an integro-differential equation for ruin probability and proved a Lundberg-type inequality corresponding to the ruin probability by means of martingale methods [3]. Gerber and Shiu [5] and Gerber and Landry [6] continued studying the expected discounted penalty function and the time value of ruin. For more details and new developments on the perturbed risk process, the interested readers can refer to [7-13].

Other kinds of generalizations for the classical risk process are inspired by the extensive investigations of both risk and portfolio fluctuations. For instance, the continuous-time risk processes with stochastic interest have been studied by many authors, see [14-21]. Temnov [22] described the premium income by Poisson process and derived an explicit formula for the ruin probability to the corresponding risk process.

Motivated by the above findings, this study aims at gaining an insight into the effects of stochastic premium incomes under perturbation. In this paper, we will consider a double compound Poisson-Geometric risk model with diffussion in which the arrival of policies and claims follows compound Poisson-Geometric process, respectively. Then we study the adjustment coefficient equation, ruin probability and the time to reach a given level.

2. The Risk Model

Definition 1 A distribution is said to be Poisson-Geometric distributed, denoted by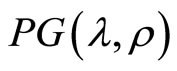, if it’s generating function is

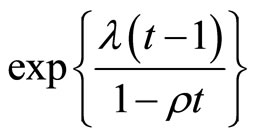
where,.

Definition 2 Let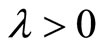 and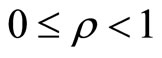, then

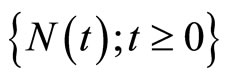is said to be a Poisson-Geometric process with parameters, , 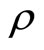if it satisfies 1);

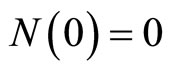2) 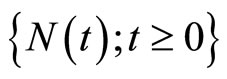has stationary and independent increments；

3)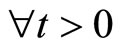, is a Poisson-Geometric distributed with parameters, , 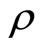and

,.

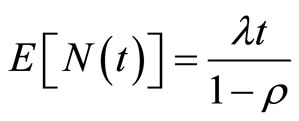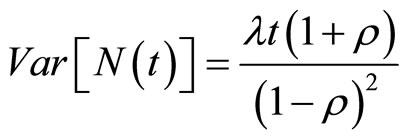Let denote the surplus at time t. Then the double compound Poisson-Geometric risk model with interfereence is defined as

(1)

where, is the initial capital, 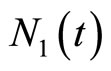is the number of premium up to time t, and follows a PoissonGeometric distribution with parameters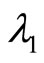,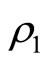; 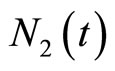is the number of claims up to time t, and follows a Poisson-Geometric distribution with parameters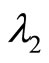,. Let the size or amount of the k th claim be and 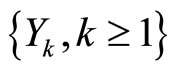be a sequence of i.i.d. nonnegative random variables with mean, variance 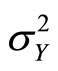and moment generating function. 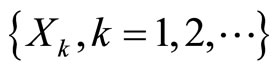are positive i.i.d. random variables representing the successive premium amounts with mean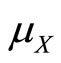, variance 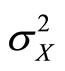and moment generating function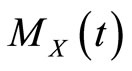. 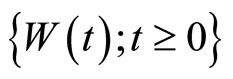is standard Brownian motion with 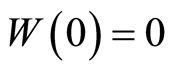and is a constant, representing the diffusion volatility parameters.

Throughout this paper, we assume that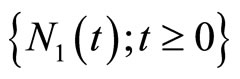, , 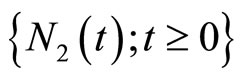, 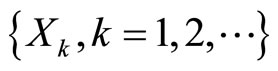and 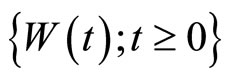are mutually independent.

In order to ensure the insurance company’s stable operation, we assume

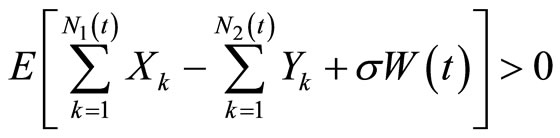
which implies

Let

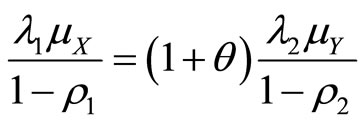
then 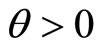is the relative security loading factor.

For the risk model (1), the time to ruin, denoted by T, is defined as

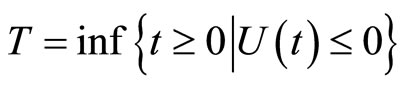
and define the ruin probability with an initial surplus 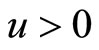by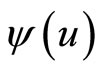, namely

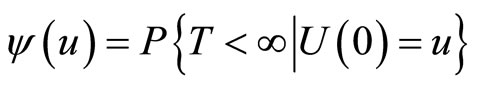(2)

3. The Property of the Profits Process

Define the profits process by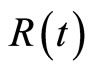, i.e.

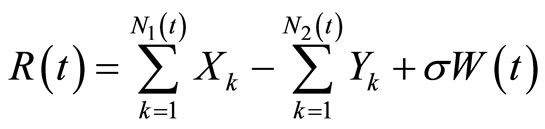(3)

It is obviously, we have

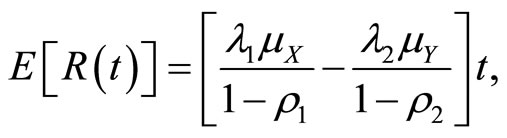
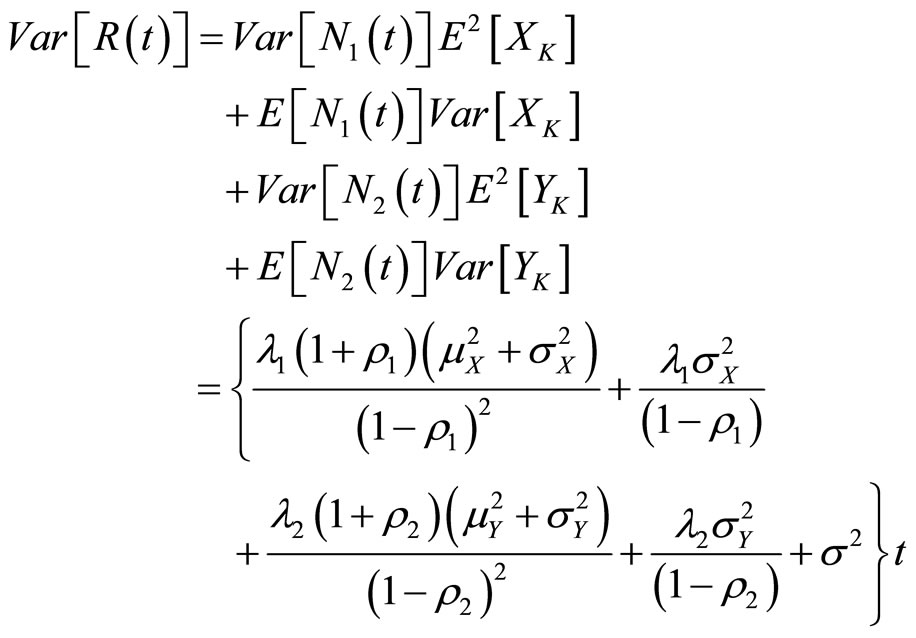
Let

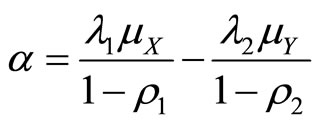
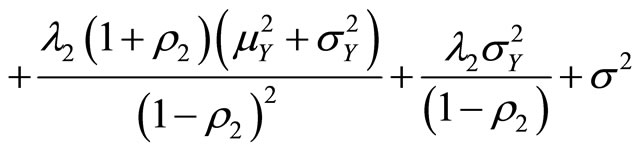
then

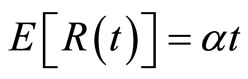
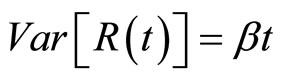
Lemma 1 The profits process 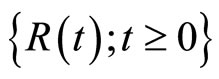has the following properties:

1);

2) has stationary and independent increments.

Theorem 1 For the profits process, there has a function such that

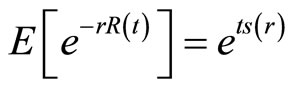(4)

Proof

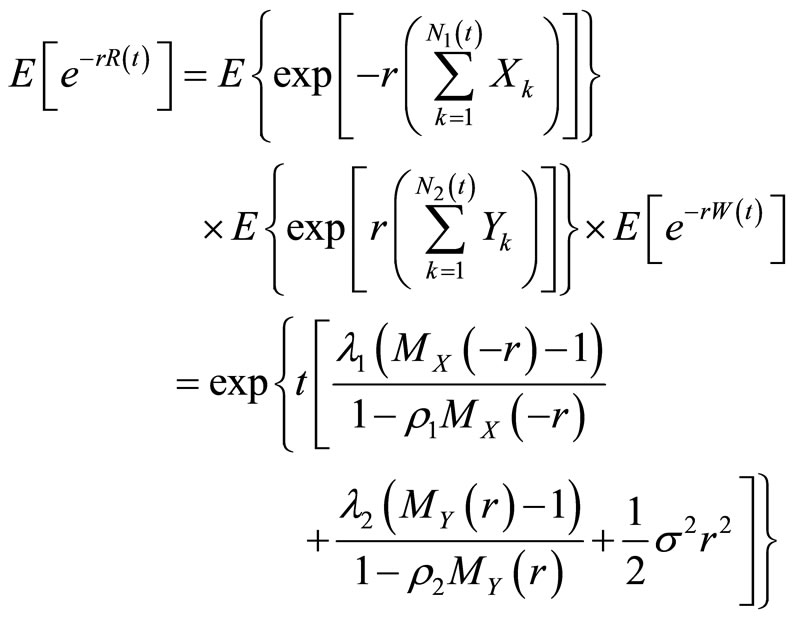
Let

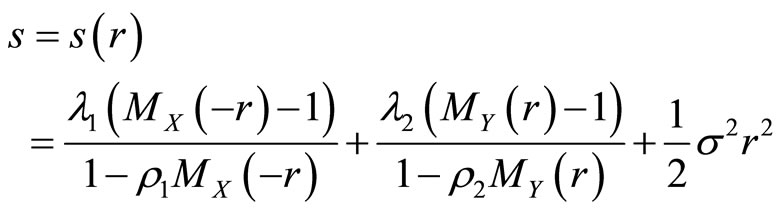(5)

Theorem 2 The equation

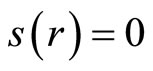(6)

has a unique positive solution, and the Equation (6) is said to adjustment coefficient equation of the risk model (1).

Proof From (5), we have

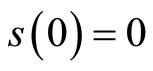
and since

,

, ,

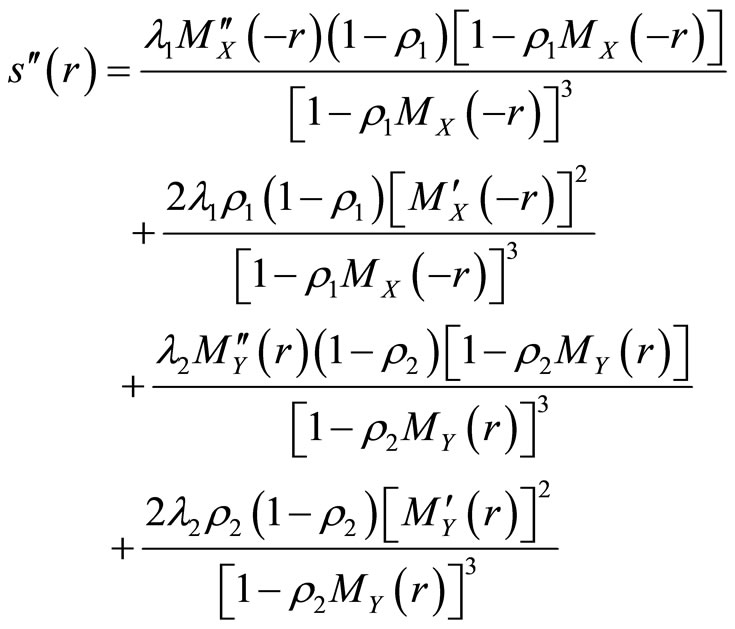
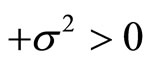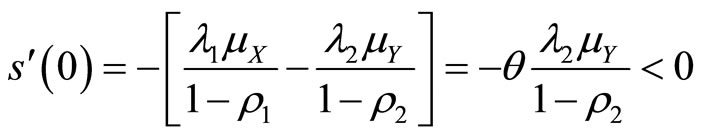we see that is a convex function on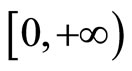, and since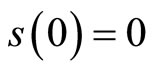, 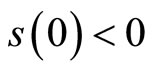and, then it can be shown that 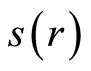has has a unique positive soluti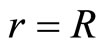on on.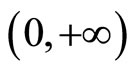

For the profits process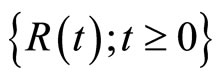, let

.

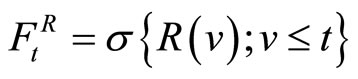Theorem 3 If r and s satisfy the Equation (5), then the surplus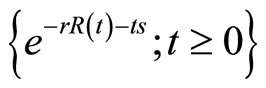is a martingale.

Proof

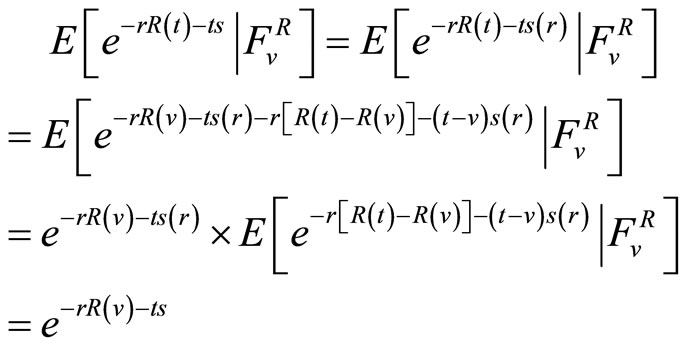
Theorem 4 T is a stopping time for.

Theorem 5 The probability of the risk model (1) is

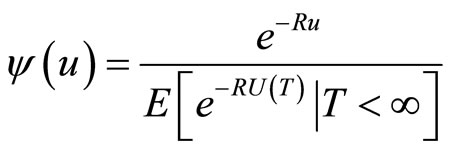(7)

Corollary.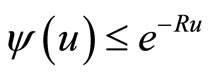

4. The Time to Reach a Given Level

Let

Then is the time when the surplus reaches a given level firstly.

Theorem 6 The Laplace transform of is

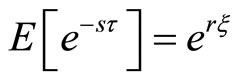(8)

where r satisfies (6).

Proof For the surplus process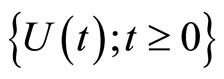, using the theorem of martingale and stopping time, we see that is a stopping time of. Let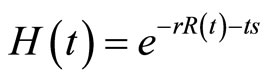, by Theorem 3 the surplus 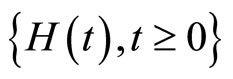is a martingale, hence we have

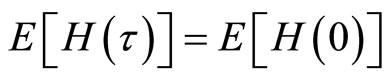
implying that

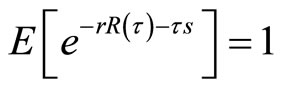
Since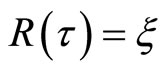, so we get

.

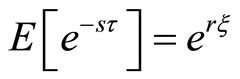Theorem 7 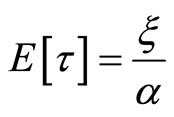and

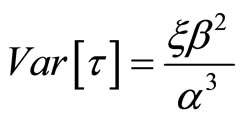(9)

Proof Using Theorem 6, we have

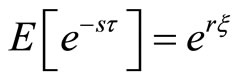
Suppose

(10)

then                

and

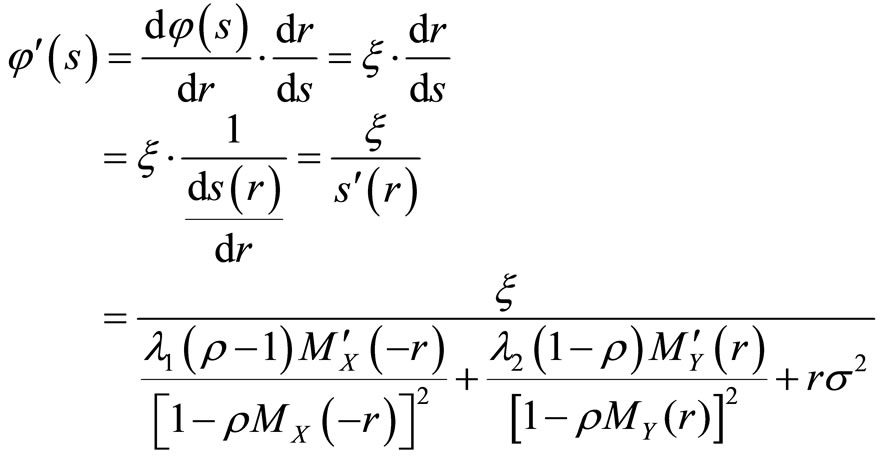
Let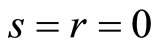, then we get

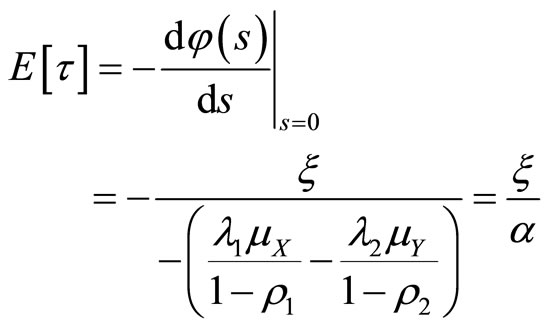
Similarly,

.

Let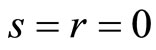, we have

REFERENCES