Journal of Mathematical Finance
Vol.06 No.05(2016), Article ID:72083,18 pages
10.4236/jmf.2016.65055
Critical Re-Examinations on the Relationships among Capital Structure, Costs of Capital, and Firm Value
Chengho Hsieh1, Tibor Szarvas2
1Department of Economics and Finance, School of Business, College of Business, Education and Human Development, Louisiana State University-Shreveport, Shreveport, LA, USA
2Department of Mathematics, School of Mathematics and Sciences, College of Arts and Sciences, Louisiana State University-Shreveport, Shreveport, LA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 30, 2016; Accepted: November 14, 2016; Published: November 17, 2016
ABSTRACT
We define debt ratio as the market value of a firm’s debt divided by the market value of the firm. In a perfect market with corporate taxes, given that the cost of debt is increasing and concave up and that the firm rebalances its debt, the cost of equity is an increasing and concave up function of the debt ratio if and only if the third derivative of the cost of debt is non-negative; otherwise, the cost of equity is increasing but its exact shape cannot be ascertained. In all cases, however, the cost of equity must be concave up initially. Also in this world, the weighted average cost of capital of the firm, WACC, is decreasing and concave down. In an imperfect market, the WACC may not have an absolute minimum between zero and 100 percent debt. Even if it does, the minimum may not occur at the debt ratio that maximizes firm value. The “pure-play” method to determine a new project’s discount rate is correct only if the opportunity cost of capital of the comparable firm remains constant with respect to the debt ratio or if the debt ratio of the comparable firm is equal to the target debt ratio of the firm evaluating the project. Strictly speaking, even if the two debt ratios are the same, the opportunity cost of capital of the comparable firm is not necessarily equal to that of the project unless the two costs of capital are identical functions of the debt ratio. Therefore, this method may not be valid.
Keywords:
Capital Structure, Optimal Capital Structure, Cost of Capital, WACC, Project Cost of Capital

1. Introduction
[1] and [2] define the relationships among capital structure, costs of capital, and firm value in a perfect market with or without corporate taxes. When corporate taxes are absent, the use of debt does not change the present value of future cash flows generated from the assets and thus there is no “optimal capital structure”, the unique combination of debt and equity that maximizes the value of the firm. The weighted average cost of capital of the firm remains constant across debt ratios. [3] shows that these results hold even if debt is risky. If corporate taxes exist, the value of the firm is an increasing function of the debt ratio, resulting in an optimal capital structure that is approaching 100% debt. Meanwhile, the weighted average cost of capital is a decreasing function of the debt ratio, reaching the minimum at the same debt ratio. [4] shows that these results hold regardless of whether the debt is risk-free or risky.1
Later authors examine how market imperfections such as bankruptcy costs and agency costs affect firm value and the choice between debt and equity. When bankruptcy imposes significant monetary penalties on the firm, corporate financing decisions become a trade-off between interest tax savings and bankruptcy costs, resulting in an optimal capital structure somewhere between zero and 100% debt. These results can be seen in [5] - [10] . Later literature replaces bankruptcy costs with financial distress costs for a more general treatment on this issue.
[11] posits that due to agency costs, the firm’s expected cash flow stream is not independent of its ownership structure and that this fact may affect the choice between debt and equity. The agency cost of equity is a decreasing function of the debt ratio while the agency cost of debt is an increasing function. An optimal combination of debt and equity may exist that minimizes total agency costs and thus maximizes firm value.
Combining the considerations on interest tax savings, financial distress costs, and agency costs emerges the trade-off capital structure theory, in which the value of the firm is maximized when the optimal trade-off between the savings and the costs is reached. Less well explored, however, is how the inclusion of these costs affects the firm’s costs of capital. Nevertheless, the general view is that the cost of debt is an increasing and concave up function of the debt ratio, the cost of equity is an increasing function of the debt ratio, and that there exists a unique capital structure between zero and 100% debt that simultaneously maximizes the firm value and minimizes the weighted average cost of capital. However, no explanation can be found in the literature on why the weighted average cost of capital should simultaneously reach the minimum. Most likely, researchers simply assume that the firm’s expected cash flow stream is invariant to changes in the debt ratio. With this assumption, the present value of the expected cash flow stream is maximized when the discount rate, namely, the weighted average cost of capital, is at its lowest. However, is this assumption valid when market imperfections such as financial distress and agency costs exist?
As mentioned above, the cost of debt, cost of equity, and weighted average cost of capital are expressed as functions of the debt ratio in general, but the debt ratio is defined either as the debt to firm value ratio or the debt to equity value ratio. This inconsistency causes unnecessary confusion. In this paper, we use a single definition of debt ratio to reconstitute capital structure and cost of capital theories. In the process, we clarify the relationships among capital structure, costs of capital, and firm value in perfect and imperfect markets. In a perfect market, if the debt is risky and the firm rebalances its debt, the cost of equity is an increasing and concave up function of the debt ratio if and only if the third derivative of the cost of debt is non-negative; otherwise, the cost of equity is increasing but its exact shape cannot be ascertained. In all cases, however, the cost of equity must be concave up initially. Also in this world, the weighted average cost of capital is decreasing and concave down. In an imperfect market, the weighted average cost of capital may not have an absolute minimum between zero and 100% debt. Even if such minimum exists, the maximum firm value and the minimum weighted average cost of capital may not occur at the same debt ratio.
In the next section, we review the literature, develop our arguments, and provide the clarifications. Based on the findings in this section, we show in Section 3 that the validity of the popular “pure-play” method to estimate a project’s cost of capital is uncertain. Concluding remarks are provided in Section 4.
2. The Theories, Discussions, and Clarifications
2.1. Perfect Market
2.1.1. Risk-Free Debt
In the Modigliani and Miller theorems (1958, 1963), the cost of debt is equal to the risk-free rate Rf, and the cost of equity Ks is equal to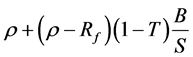 , where
, where
ρ = the discount rate for an all-equity firm;
B = the market value of debt;
S = the market value of equity;
T = the corporate income tax rate.
Let V be the market value of the firm, thus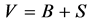 . The firm’s weighted average cost of capital, WACC, is equal to
. The firm’s weighted average cost of capital, WACC, is equal to
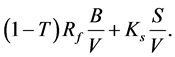
Substituting 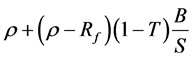 for KS in the above equation and simplifying the result, we obtain
for KS in the above equation and simplifying the result, we obtain
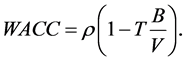
The firm’s opportunity cost of capital, Ka, is equal to
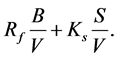
Again, substituting 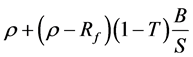 for KS and simplifying the result, we obtain
for KS and simplifying the result, we obtain
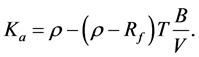
If ,
, 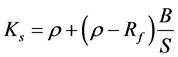 and
and 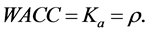
Note that both Ka and WACC are functions of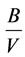 ; while Ks is a function of
; while Ks is a function of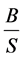 . The
. The
market value of the firm when it is levered, VL, comes from the value of operations and the value of interest tax shields:
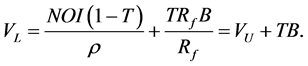 (1)
(1)
NOI is the expected net operating income, VU is the value of the firm when it is unlevered and TB is the value of interest tax shields. If T = 0, VL = VU.2 For the purposes of this paper, we change the notations for KS, WACC, and Ka and express all of them as
functions of the debt ratio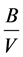 , letting
, letting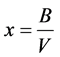 . Thus
. Thus



s(x) in Equation (2) is thus defined on the interval [0, 1). From Equations (3) and (4), if



and
Therefore, s(x) is an increasing and concave up function of x. In summary, if debt is risk-free, there is no debt rebalancing, and
2.1.2. Risky Debt
Let f(x) denote the cost of debt. It is generally accepted that for risky debt, f(x) is an increasing and concave up function of x; that is, 



we can express s(x) from the above equation as follows:
Figure 1. The shapes of s(x), r(x), and w(x) in a perfect market with corporate taxes, risk-free debt, and without debt rebalancing.
What is the behavior of s(x)? It is commonly believed that the cost of equity is an increasing function of the debt ratio. [12] argues that beyond a certain debt ratio, debt- holders begin sharing the firm’s business risk; consequently, the cost of equity should be concave down. It appears necessary to further examine the behavior of s(x), espe-
cially if the debt ratio is defined as x instead of
and concave up and r(x) is constant, s(x) is strictly increasing. The proof is given in the following.
Proposition 1:
Suppose f(x) is twice continuously differentiable on [0, 1], increasing, and concave up. Let 



Proof:
We first note that



To see that
on
Since

Introducing the notation 

that
First note that


Next, we claim that 




By the Mean Value Theorem for derivatives, there exists a d with 

However, using the fact that 


which is a clear contradiction, showing that no c with 

If the third derivative of f(x), 
Proposition 2:
Suppose 









Proof:
It will be sufficient to show that 


and since 


This last inequality is equivalent to

On the other hand, since


for some

Since by assumption 


where in the last inequality we used the facts that 

Thus we can conclude that

and since 

Proposition 3:
Suppose f(x) is twice continuously differentiable on




Proof:
Using the formula for 


It is now sufficient to see that the above expression is positive. Thus we aim to prove that

By the Mean Value Theorem for derivatives, there exists 

and since 

as needed.
Example 1 in Appendix shows the possibility of an increasing and eventually concave down s(x).6 In this example, f(0) = 0.02 and s(0) = 0.07. The reasons to use these numbers are given later in this Section. What is the behavior of w(x)?
Based on this equation,

and
Therefore, w(x) is a decreasing and concave down function of x. In summary, if debt is risky, 
If [12] is correct in that s(x) eventually concaves down, Figure 2 then becomes: Figure 3.
Again, the market value of the firm when it is levered, VL, comes from the value of operations and the value of interest tax shields:

Figure 2. The shapes of f(x), s(x), r(x), and w(x) in a perfect market with risky debt, corporate taxes, and constant debt rebalancing.
Figure 3. The shapes of f(x), s(x), r(x), and w(x) in a perfect market with risky debt, corporate taxes, and constant debt rebalancing, assuming that at higher debt ratios, bondholders share business risk.
In this equation, VTS is the value of the tax shields. Since ρ is greater than f(x),7 VTS is less than TB in Equation (1).8 Also,

Equation (6) is commonly known as the WACC method. Equations (5) and (6) are in fact equivalent. Multiplying both sides of Equation (6) by
Substituting 
Equation (5). We will assess firm value in an imperfect market based on Equation (6) in the following Section; therefore, this proof is necessary to ensure the continuity of the theory. Moreover, this proof implies that the WACC method requires constant debt rebalancing.
2.2. Imperfect Market
In an imperfect market, the trade-off capital structure theory posits that the value of the firm is a trade-off among the interest tax shields, agency costs of equity, financial distress costs, and agency costs of debt. The optimal trade-off is reached at a certain debt ratio, denoted by x*, between zero and 100%, at which the value of the firm is maximized. Based on this theory, researchers posit that corresponding to the rise and fall of the firm value, w(x) would first decrease, reach a minimum at x*, and then rise. In other words, the firm value would reach the peak and w(x) would reach the minimum at x*; therefore, x* is the optimal debt ratio. For convenience, let’s call this result the “maximum-minimum proposition.” The relationships among s(x), f(x), and w(x) can be depicted in the following Figure 4.
Note that s(0) is equal to f(1); meaning that the cost of debt when the debt ratio is 100% equals the cost of unlevered equity. There is no discussion in the literature of whether f(1) should be equal to, higher than, or lower than s(0).
Furthermore, no justification can be found in the literature for the “maximum- minimum proposition”. In other words, no clear explanation has been offered for why w(x) should be U-shaped with an absolute minimum between zero and 100% debt and why the maximum firm value and the minimum of w(x) should occur at the same debt ratio. Most likely this proposition is based on the assumption that the firm’s expected cash flow stream is invariant to changes in debt ratio; therefore, the value of the firm is maximized when the discount rate, w(x), is minimized. However, if this result stems
Figure 4. The possible shapes of f(x), s(x), and w(x) in an imperfect market under the conventional view that there is a unique debt ratio that maximizes firm value and minimizes w(x).
from the trade-off capital structure theory, can we make such an assumption? [12] points out that the firm’s future operating income may not be the same for all debt ratios and as a consequence, maximizing firm value and minimizing w(x) may not occur at the same debt ratio. In the following, we give a formal analysis on this issue.
According to the trade-off theory, the financial distress costs and the agency costs of debt are expected to increase with debt ratio; while the agency costs of equity are expected to decrease with the debt ratio. Thus, if market imperfections exist, NOI(1 − T) in Equation (6) may vary across debt ratios, depending on the likelihood for these costs to occur and the magnitude of these costs.9 In short, we may not hold expected cash flow stream constant across debt ratios.
In Equation (6), w(x) should reflect systematic risks. According to the literature, financial distress and debt-related agency problems are more likely to occur during economic downturns.10 Therefore, the costs incurred by these problems may present systematic risks, and r(x) and w(x) should reflect these risks. Again according to the trade-off theory, these problems become more severe with the increase of debt ratio; therefore, the systematic risks reflected in r(x) and w(x) should also increase. In addition, according to the literature, financial distress and debt-related agency problems give management the incentive to change the firm’s assets. For example, financial distress costs include the loss incurred by fire-selling assets, and debt-related agency problems include switching to more risky assets and “cashing-out.”11 Changing the assets is likely to change the asset risk (and thus the systematic risk). Again, since a higher debt ratio increases the probability for financial distress and debt-related agency problems to occur, the resulting impact on asset risk should also be reflected in r(x) and w(x). Based on these arguments, r(x) and w(x) may not have the same functions as depicted in Figure 2 and Figure 3. The “maximum-minimum proposition” argues for a U-shaped w(x), but there is no proof to support it.
To use Equation (6), we need to determine how the financial distress and agency problems affect both the numerator and denominator of the equation for a given debt ratio. This appears to be an impossible task, given the current state of literature. Therefore, we can’t say for sure how VL and w(x) behave as functions of the debt ratio in an imperfect market. Taking the first derivative of w(x) with respect to x,
Here, in addition to the assumptions made about f(x), we assume that s(x) is continuously differentiable and increasing on

Given T, f(0), and s(0), the value of 





The behavior of r(x) in an imperfect market has not been examined in the literature. Both r(x) and w(x) reflect the firm’s asset risk; therefore, both must have a certain relationship. In the following, we prove that the first derivative of r(x) is greater than that of w(x).
Proposition 4:
Suppose 







Proof:
First observe that

and thus

since 

Based on Proposition 4, when w(x) is decreasing, r(x) could still be rising or could be also decreasing but at a slower rate, and when w(x) is rising, r(x) must also be rising but at a faster rate. Thus, r(x) cannot be a constant if w(x) is U-shaped, implying a changing asset risk across the debt ratios.15
The proponents of the “maximum-minimum proposition” would need to explain why expected cash flow stream can be assumed constant across debt ratios in the world of the trade-off capital structure theory, if this is an assumption for the proposition. They would also need to explain how and why the asset risk is perceived changing across debt ratios in the way implied by the shape of r(x) discussed in the last paragraph. Also, as mentioned earlier, financial distress costs and agency costs involve possible changes in the firm’s assets and their occurrences are functions of the debt ratio; therefore, there is no guarantee that s(0) = f(1) = ρ. f(1) may be higher than, equal to, or lower than s(0). This potentially adds complications to the shapes of r(x) and w(x). In Appendix, Examples 2, 3, and 4 show possible shapes of r(x) and w(x) when f(1) = s(0), f(1) > s(0) and f(1) < s(0) respectively. In each example w(x) does not have an absolute minimum between zero and 100% debt; also, since the slope of s(x) is greater than 0.057, w(x) is initially increasing. Although s(x) and f(x) in each example are specified arbitrarily, they satisfy the conditions that


If expected cash flows may not be held constant across debt ratios and if the function of w(x) cannot be determined, what can we say about a firm’s optimal capital structure in an imperfect world? In a nutshell, the optimal capital structure, if exists, can be anywhere from zero to 100% debt depending on the expected cash flows and w(x) at each debt ratio. w(x) may not be U-shaped as conventionally believed. Even if w(x) has an absolute minimum between zero and 100% debt, there is no guarantee that the debt ratio that minimizes w(x) also maximizes the value of the firm. This result does not prescribe a specific shape of w(x) and hence r(x), and does not specify whether f(1) is equal to, higher than, or lower than s(0).
3. Firm Opportunity Cost of Capital and Project Evaluation
Based on the aforementioned analysis, the firm’s opportunity cost of capital r(x) may not be a constant across the debt ratio in an imperfect world. A non-constant r(x) poses a major difficulty in evaluating a new project. It is necessary to assess a project’s risk to determine the project’s opportunity cost of capital r(x)j and hence the project’s weighted average cost of capital w(x)j to calculate the net present value. Since the risk of a new project is usually difficult to determine, the “pure play” method is often used. In this method, r(x) of a comparable firm whose entire business is similar to the project is calculated based on the firm’s f(x), s(x), and x.16 Since the comparable firm and the project are of the same business, r(x) is used as r(x)j.
In this equation, xj is the debt ratio for the project. Based on current literature, it should be equal to the target debt ratio of the firm that is considering the project (henceforth “the project firm”). f(x)j is the cost of debt and s(x)j is the cost of equity for the project; both are determined by xj and by the project’s risk. The debt ratio for the comparable firm may not be the same as the target debt ratio for the project firm; that is, x may not be equal to xj. If they are not equal, f(x) is not equal to f(x)j and s(x) is not equal to s(x)j, although the project risk is deemed equal to that of the comparable firm. A typical procedure is to first estimate f(x)j based on the project’s risk and xj and then solve for s(x)j based on the now known r(x)j, f(x)j, and xj. The project’s weighted average cost of capital, w(x)j, can then be calculated:
However, this method is valid only if the opportunity cost of capital is constant with respect to debt ratio or if x happens to be equal to xj. If the opportunity cost of capital is not constant, r(x) is not necessarily equal to r(x)j unless x is equal to xj. Strictly speaking, even if the two debt ratios are equal, r(x) is not necessarily equal to r(x)j unless r(x) and r(x)j are identical functions of the debt ratio. We can’t say for sure that they are. If r(x) cannot be used to proxy r(x)j, the “pure-play” method breaks down because the cost of capital for the project cannot be determined.
4. Conclusions
Theories in capital structure and costs of capital are important because they lay the foundation for making financing and investment decisions in a firm. However, inconsistent and questionable arguments exist concerning the relationships among capital structure, costs of capital, and firm value. We critically re-examine these relationships and provide several clarifications.
We define the debt ratio as the market value of the debt divided by the market value of the firm, and express the cost of debt, cost of equity, the firm’s opportunity cost of capital, and the weighted average cost of capital as functions of this debt ratio. In a perfect market with corporate taxes, given that the cost of debt is increasing and concave up and that the firm rebalances its debt, the cost of equity is increasing and concave up if and only if the third derivative of the cost of debt is non-negative; otherwise, the cost of equity is increasing but its exact shape cannot be ascertained. In all cases, however, the cost of equity must be concave up initially. Also in this world, the weighted average cost of capital is decreasing and concave down.
In an imperfect market, the optimal capital structure can be anywhere from zero to 100% debt, depending on the expected cash flows and the weighted average cost of capital at each debt ratio. We can’t say for sure that the weighted average cost of capital has an absolute minimum between zero and 100% debt. Even if such minimum exists, the debt ratio that results in this minimum may not be the one that maximizes the firm value. These results are contrary to the conventional view that there exists a unique debt ratio between zero and 100% that simultaneously minimizes the weighted average cost of capital and maximizes the firm value. The proponents of this view would need to explain how the expected cash flow stream can be assumed constant across debt ratios in the context of the trade-off theory, if this is an assumption. We prove that if the weighted average cost of capital is U-shaped, the firm opportunity cost of capital cannot be a constant across debt ratios. Since the opportunity cost of capital reflects asset risk, the proponents would also need to explain how and why the asset risk is perceived changing across debt ratios in the way implied by the shape of the opportunity cost of capital.
The “pure-play” method to determine a new project’s discount rate is correct only if the opportunity cost of capital remains constant with respect to debt ratio or if the debt ratio of the comparable firm is equal to the target debt ratio of the firm evaluating the project. Strictly speaking, even if the two debt ratios are the same, the opportunity cost of capital for the comparable firm is not necessarily equal to that for the project unless the two costs of capital are identical functions of the debt ratio. Therefore, this method may not be valid.
Cite this paper
Hsieh, C. and Szarvas, T. (2016) Critical Re-Examinations on the Relationships among Capital Structure, Costs of Capital, and Firm Value. Journal of Mathematical Finance, 6, 792- 809. http://dx.doi.org/10.4236/jmf.2016.65055
References
- 1. Modigliani, F. and Miller, M.H. (1958) The Cost of Capital, Corporation Finance, and the Theory of Investment. American Economic Review, 48, 261-297.
- 2. Modigliani, F. and Miller, M.H. (1963) Corporate Income Taxes and the Cost of Capital: A Correction. American Economic Review, 53, 433-443.
- 3. Stiglitz, J.E. (1969) A Re-Examination of the Modigliani-Miller Theorem. The American Economic Review, 59, 784-793.
- 4. Rubinstein, M.E. (1973) A Mean-Variance Synthesis of Corporate Financial Theory. The Journal of Finance, 167-181.
http://dx.doi.org/10.1111/j.1540-6261.1973.tb01356.x - 5. Robichek, A.A. and Myers, S.C. (1966) Problems in the Theory of Optimal Capital Structure. The Journal of Financial and Quantitative Analysis, 1, 1-35.
http://dx.doi.org/10.2307/2329989 - 6. Baxter, N.D. (1967) Leverage, Risk of Ruin and the Cost of Capital. The Journal of Finance, 22, 395-403.
http://dx.doi.org/10.1111/j.1540-6261.1967.tb02975.x - 7. Stiglitz, J.E. (1972) Some Aspects of the Pure Theory of Corporate Finance: Bankruptcies and Takeovers. The Bell Journal of Economics and Management, 3, 458-482.
http://dx.doi.org/10.2307/3003033 - 8. Kraus, A. and Litzentberger, R.H. (1973) A State-Preference Model of Optimal Financial Leverage. The Journal of Finance, 28, 911-922.
http://dx.doi.org/10.1111/j.1540-6261.1973.tb01415.x - 9. Scott Jr., J.H. (1976) A Theory of Optimal Capital Structure. The Bell Journal of Economics, 7, 33-54.
http://dx.doi.org/10.2307/3003189 - 10. Kim, E.H. (1978) A Mean-Variance Theory of Optimal Capital Structure and Corporate Debt Capacity. The Journal of Finance, 33, 45-63.
http://dx.doi.org/10.1111/j.1540-6261.1978.tb03388.x - 11. Jensen, M.C. and Meckling, W.H. (1976) Theory of the Firm: Managerial Behavior, Agency Costs, and Ownership Structure. Journal of Financial Economics, 3, 305-360.
http://dx.doi.org/10.1016/0304-405X(76)90026-X - 12. Brealey, R.A., Myers, S.C. and Allen, F. (2014) Principals of Corporate Finance. 11th Edition, McGraw-Hill, Irwin, 438.
Appendix
Example 1. This example shows that if 










Example 2. Possible shapes of r(x) and w(x) when
Example 3. Possible shapes of r(x) and w(x) when
Example 4. Possible shapes of r(x) and w(x) when
NOTES
1 [1] [2] [4] do not assume that the firm rebalances its debt to maintain the debt ratio over time.
2 [1] [2] do not assume that the firm rebalances its debt to maintain the debt ratio over time. If this assumption is made, the expected interest tax shields would have a risk equal to the firm’s operations and should be discounted at ρ, and 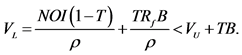
3The discussions up to this point are within the frameworks of [1] [2] . However, the discussions are based on the debt ratio of x, instead of



4This means that the first and second derivatives exist and are continuous on [0, 1].
5Using the continuity of


6Although f(x) in this example is specified arbitrarily, it satisfies the conditions that 

7ρ is greater than f(x) except when x = 1.
8If there is no debt rebalancing, the tax shields have a risk equal to the debt, thus the discount rate should be f(x), and

9The gain from tax shields is accounted for by using the after-tax cost of debt in w(x).
10Indeed, debt agency costs are often treated as part of the financial distress costs.
11In “cashing-out,” the management liquidates assets for cash and pay out the cash as dividends to benefit shareholders at the expense of the debtholders.
12The assumptions for f(x) are 

13The unlevered equity risk premium is thus equal to
14The differentiability of r(x) and w(x) follows from the assumptions.
15Also, as proved earlier, if f(x) is increasing and concave up and r(x) is constant, w(x) must be decreasing and concave down (see Figure 2 and Figure 3). The contra-positive statement is that if w(x) is in a different shape such as U-shape, r(x) cannot be a constant. Although Equation (6) requires constant debt rebalancing, r(x) is not necessarily a constant when market imperfections are allowed.
16
























