ABSTRACT

Consider an ephemeral sale-and-repurchase of a security resulting in the same position before the sale and after the repurchase. A sale-and-repurchase is a wash sale if these transactions result in a loss within ±30 calendar days. Since a portfolio is essentially the same after a wash sale, any tax advantage from such a loss is not allowed. That is, after a wash sale a portfolio is unchanged so any loss captured by the wash sale is deemed to be solely for tax advantage and not investment purposes. This paper starts by exploring variations of the birthday problem to model wash sales. The birthday problem is: Determine the number of independent and identically distributed random variables required so there is a probability of at least 1/2 that two or more of these random variables share the same outcome. This paper gives necessary conditions for wash sales based on variations on the birthday problem. Suitable variations of the birthday problem are new to this paper. This allows us to answer questions such as: What is the likelihood of a wash sale in an unmanaged portfolio where purchases and sales are independent, uniform, and random? Portfolios containing options may lead to wash sales resembling these characteristics. This paper ends by exploring the Littlewood-Offord problem as it relates capital gains and losses with wash sales.

Keywords:

Wash Sales, Tax, Birthday Problem, Littlewood-Offord, Probability, Finance

1. Introduction

Wash sales occur when a security is sold and quickly bought back with the sole intent to capture a tax loss from the sale. Wash sales impact a portfolio’s tax liabilities. Deter- mining the likelihood of wash sales is also important for understanding investment strategies and for comparing actively and passively managed portfolios. Wash sales apply to investors, but not to market makers.

Taxes play a significant role in economics and finance. Taxes influence behavior, shape the engineering of financial transactions, and sometimes have unintended consequences. Therefore, thoughtful analysis is imperative for taxes. This paper adds firm mathematical foundations to aid the understanding of wash sale taxes.

The main goal of this paper is: To provide foundations for certain wash sales-in cases when they may occur as well as the capital gain implications. This may also help differentiate managed funds and unmanaged index funds in terms of wash sales.

Wash sales are sometimes created by the exercise of options, thus a portfolio manager may not be able to avoid a wash sale in some contexts. For example, suppose an in-the-money American-style put option is written in a portfolio. Provided this option remains in-the-money, it may be exercised by its holder¹ at anytime up to its expiry. If the exercise of this put option replaces shares sold at a loss in the prior 30 days, then this is a wash sale. This option’s exercise is beyond control of the portfolio manager.

The foundations given here start with variations of the classical birthday problem from probability theory [1] - [3] . This work has implications on wash sales. Also, the Littlewood-Offord problem [4] - [6] is applied to understand capital gains for certain wash sales. The Littlewood-Offord problem is viewed from the perspective of the pro- babilistic method.

For convenience, let.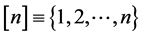

1.1. Wash Sales in Detail

Suppose a security is sold at a loss on day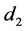. This sale is a wash sale if substantially the same security is purchased within 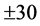calendar days from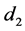, see for example [7] .

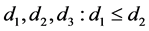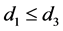Definition 1 (US wash sale [7] ) Consider three dates and where 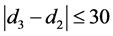calendar days. Suppose s shares of a security are purchased on date 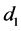at price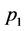. At some later date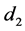, s shares are sold for price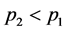. Thus, the s shares are sold at a loss. Then within 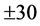days on date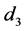, s shares are repurchased for price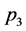. This is a wash sale and since 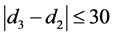days, then the next adjustments must be made [7] :

1) The loss 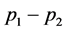is not permissible for taxes. That is, this loss may not be subtracted from profits or gains and it may not be used to get a lower tax rate.

2) The cost-basis of the shares repurchased on 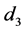is set to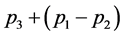. The shares purchased on have the start of their holding period reset to.

Short positions may also be wash sales. For example, consider holding a short position of 100 shares of a security starting on date in a portfolio. Then suppose this short position is closed at a loss by purchasing 100 shares on day. Once this position is closed on day, then contains no shares of this security. Next re-short another 100 shares of substantially the same security on where days. These transactions leave the portfolio the same while getting a tax advantage for the loss. This tax advantage is also disallowed by the wash sale rules.

Consider a wash sale as described by Definition 1, where or in other words. Suppose the shares are sold at price at the later date. In the case with the wash sale, there is a capital gain of which is smaller than the capital gain if the wash sale had not occurred. Capital gains are taxable. A capital gain is from the single purchase of the shares for price on and the single sale of the shares on date for price, thus skipping the sale at a loss and repurchase.

This means such a wash sale gives or less taxable income than a single purchase of the security at price on date and a single sale for price on. Of course, a wash sale’s loss is not allowed.

Wash sales may be avoided by restricting each security in a portfolio to be either purchased or sold only every 31 calendar days. This restriction may not be suitable for many portfolios. In a portfolio containing options, it may be impossible to maintain this restriction.

It has also been suggested, e.g. [9] , wash sales may be avoided by purchasing or selling (moderately) correlated, but not substantially the same, securities. That is, if a security is sold at a loss then purchase a different but correlated security within 30 days maintaining some of a portfolio’s characteristics while keeping the tax advantage.

Historically many securities are assumed to only trade on about business days per year [10] . Although reflecting on global markets one may assume there are trading days.

1.2. Background

There has not been much research on wash sales, e.g., [9] . There is important work on taxation and its investment implications. Take, for example, [11] - [13] .

The birthday problem is classical.

Definition 2 (Birthday-Collision) Given two random variables mapping respectively to in the same range, then a birthday-collision is when.

To model random wash sales, this paper assumes independent identically distributed random variables. A common statement of the birthday problem is:

Definition 3 (Birthday Problem) Consider n days in a year and k independent identically distributed (iid) uniform random variables whose range is and. What is the probability of at least one birthday-collision among these k random variables?

According to a blog post by Pat B [14] the birthday problem may have originally been given by Harold Davenport as cited in [15] and later published by [1] . In any case, von Mises gave the first published version to the best of our knowledge.

Bounds of day counts for the birthday problems include [16] who gives bounds for birthdays of distance d for both linear years as well as cyclic years. In a cyclic year, 1-January is a single day from 31-December of the same year. Bounds for birthdays of distance d for cyclic years are given by [17] .

The birthday problem applied to boys and girls (random variables with different labels) are discussed in [18] as well as [19] . That is, how many birthdays are shared by one or more boys and one or more girls? A comprehensive view is provided by [20] including stopping problems with the boy-girl birthday problem. Non-uniform bounds for online boy-girl birthday problems are given by [21] and [22] .

Tight bounded Poisson approximations for birthday problems are given by [23] . Poisson approximations to the binomial distribution for the boy-girl birthday problem is given by [19] . A Stein-Chen Poisson approximation is used by [24] to solve variations of the standard birthday problem. Matching and birthday problems are given by [25] . Incidence variables are used to study birthday problems with Pareto-type distributions in [26] .

Applications of the birthday problem include: computer security [20] [21] [26] [27] , public health and epidemiology [28] , psychology, DNA sequence alignment, experi- ments, and games [29] [30] . Summaries of work on the birthday problem are in [29] - [31] .

Results on the expectation for getting j different letter k-collisions are given by [32] . Their results are expressed as truncated exponentials or gamma functions.

The Littlewood-Offord problem hails from complex analysis [6] . Erdös [5] improved Littlewood and Offord’s result by an elegant application of the probabilistic method. These and related results determine the concentration of sums of random variables multiplied by integers. The Littlewood-Offord problem is applied to certain capital gains.

1.3. Structure of This Paper

Section 2 reviews variants the birthday problem applied here. First the classical birthday problem is discussed. Next this section progresses through the birthday problem. After the definition and key results are given about the birthday problem, the boy-girl birthday problem is explored. Finally, the boy-girl birthday problem is defined and several bounds are derived as they relate to a necessary condition for wash sales.

Subsection 2.1 gives an example of wash sales based on boy-girl birthday collisions of a single day.

Section 3 generalizes results of the previous sections. In particular, it shows how to compute, the number of b boys and g girls that give a probability of 1/2 or more where a boy and a girl have birthdays within d days of each other over n days.

Subsection 3.1 gives an example of wash sales based on boy-girl birthday collisions over a range of days.

Finally, Section 4 explores how wash sales impact capital gains and losses. Since wash sales are capital losses, they may offset capital gains. Several results, including the Littlewood-Offord problem, are applied to capital gains and losses as they may be impacted by wash sales.

2. The Birthday Problem and Wash Sales

The birthday problem is often applied to finding the probability of coincidences. So there is a rich literature on variations of the birthday problem [29] [30] . Asset sales are often viewed as carefully selected. However, portfolios using American-style options may exhibit asset sales or purchases beyond the control of the portfolio managers.

A key question is: Over n consecutive days for what integer k does

hold for k iid uniform random variables? In other words,

given n days, what is the least k iid uniform random variables so that?

Solutions to this basic variation of the birthday problem are well known. The probability is the compliment of the probability of k iid uniform random variables having no birthday-collisions. Therefore, if there are no birthday-collisions,

then k birthdays can be in permutations out of all possible mappings of the k random variables onto. In other words, the subsets of k distinct

elements of is the exact number of subsets the k variables may map to without a collision. These k variables may be ordered in permutations. That is,

(1)

for and otherwise.

Starting with n and a probability, then computing k is often done using the inequality. In particular, the smallest k giving a probability of 1/2 that there is at least one birthday-collision requires k to be roughly or about. See for example, [1] [33] [34] .

Another classical approach is to look at the random variable X as the sum of all birthday-collisions of k people over n days, see for example [19] [25] [35] [36] . A concise exposition is given in [36] which we follow. Presume the birthday of person is given by the random variable. Since a potential birthday collision is

a Bernoulli trial, so X is binomially distributed. Thus, where is the maximum number of potential birthday-collisions. The expectation of the maximum number of birthday collisions possible is with probability

where. The expected maximum number of birthday-collisions is. If n is sufficiently larger than k, then X is approximately Poisson where. Thus,.

In the case of the birthday problem, if two random variables map within d days of each other, then this is a birthday-collision [16] .

Two birthdays and of distance demark a span of size. For example, , so these dates are in a span, but not in a span of.

The next definition is based on [16] [17] [29] .

Definition 4 (±d Birthday Collisions) Consider n days in a year, spans of less than days, and k iid uniform random variables with range: Then is the probability at least two such random variables have a birthday-collision. That is, these two random variables have ranges in less than d days of each other.

In n days with a span, then gives the smallest k so

there is a probability of at least 1/2 where at least two such random variables are fewer than d days from each other.

Definition 5 (Blocks of days) Let. Suppose birthdays are ordered as, then for a birthday its nearest birthday pairs are and. There are no birthdays between and and there are no birthdays between and.

A block of days contains a single birthday on one of its end-points. The birthday is associated with two blocks: and.

The days between and form a block of size since there are no birthdays between and. Thus, two nearest birthday pairs contained in a span of are separated by a block of size.

Take k iid uniform random variables and consider birthday-collisions over days. Naus [16] gives the next idea: If there are no birthday-collisions, then there must be at least size blocks of no birthdays between each nearest birthday pair. This gives a total of days with no birthdays in contiguous blocks of at least days each. Therefore, if there are no birthday-collisions, then k birthdays can be in permutations out of all possible map-

pings of the k random variables. Thus, to get the probability of at least one birthday collision, take the compliment of the probability of having no birthday- collisions. The next result follows.

Theorem 1 ( [16] ).

(2)

for and otherwise.

Using the bound on Naus’ result gives k of about, see [16] . Also [29] approximate k to about for the cyclic version.

Note, Theorem 1 with gives the solution to the standard birthday problem of Definition 3. That is, a span of and blocks of size.

The falling factorial is

(3)

In these terms, Theorem 1 may be expressed as.

The next classic result is important.

Lemma 1 (Classical) Let. The falling factorial is the number of injective mappings of elements to the range.

The next definition is based on [18] [20] [23] .

Definition 6 (Boy-Girl Birthdays) Consider n days in a year and two sets of dis- tinctly labeled iid uniform random variables all with range: g of these variables are girls and b of these variables are boys. Then is the probability at least one girl and one boy have a birthday-collision.

For instance, in n days, gives the value and

so there is a probability of 1/2 where at least one girl and one boy have the same birthday.

Stirling numbers of the second kind [37] count the number of non-empty partitions of a given set. For example given the set, the number of partitions of into i

non-empty subsets is.

Due to their nature, it is common to define Stirling numbers of the second kind

recursively [37] : with the base cases and. Finally, for any. As an example,

(4)

The next classical equality counts the number of functions from elements to elements, ,

(5)

expressed as the number of non-empty i partitions of the elements and the number of surjections from the i partitions by Lemma 1.

Theorem 2 ( [18] [20] ) Consider n days in a year and two sets of distinctly labeled iid uniform random variables all with range: g random variables are girls and b random variables are boys. Then is the probability at least one girl and at least one boy have a birthday-collision and

(6)

The next Lemma is from [18] [38] .

Lemma 2 ( [18] [38] ) Consider n days in a year and two sets of distinctly labeled iid random variables all with range: g random variables are girls and b random variables are boys. Then is the probability that at least one girl and at least one boy have a birthday-collision and

(7)

Wash Sale Example 1: Same Day Purchase and Sale

Consider a portfolio where is asset (security) i held in. At the end of business on day, consider portfolio the market value of asset i in is and the total value of is. Just before the start of each tax year, asset i has market value and has total market value. Assume each asset is sufficiently liquid so our purchases or sales do not impact its market price.

Suppose portfolio has T total iid uniform and random transactions during the business days of one calendar year. Assume trades are distributed on an asset-weighted basis from the initial weight of each asset in the portfolio just before the trading year commences. Thus, just prior to the first trading day and with no other information,

asset is expected to have trades in one year.

Take transactions and define the independent Rademacher² random variables representing buys or sells of portions of asset class i in portfolio:

(8)

for. That is, the b independent Rademacher random variables where represent buys (boys) and the g random variables where represent sells (gals).

To apply a suitable version of Chernoff's bound ( [39] , Appendix A) where

, then for any

(9)

So, for example, take, then holds with high probability as gets large. Of course, as gets large, the likelihood of wash sales increases. That is, the total number of buys and sells is expected to converge to be about the same as the total number of transactions grows. However, along the way, the number of buys or sells may not be as balanced [2] [40] .

Select the probabilities that the number of buys and sales are the same, given total trades, in asset class are:

Let h be half the total trades. That is,. Assuming trading days gives the probabilities of same-day girl-boy birthday collisions for a single asset-type as:

In fact, and. So, considering only equal numbers of sales and buys over days of the same asset type, 14 girls and 14 boys is the first case where there is greater than a 50% chance of a (same-day) boy- girl birthday collision.

Assuming the portfolio already holds this single asset type, a boy-girl collision only is a necessary condition for a wash sale. A birthday collision must be accompanied by a sale at a loss and a repurchase of substantially the same security within 30 calendar days.

3. General Wash Sales

Necessary conditions are given here for wash sales where a purchase and sale are within calendar days. Since the purchase and sale are not known to be at a loss while keeping substantially the same portfolio before and after the birthday collision.

Definition 7 (Boy-Girl Birthdays) Consider n days in a year, spans of days, and two sets of distinctly labeled iid uniform random variables all with range: g random variables are girls and b random variables are boys. Then is the probability at least one girl and one boy are mapped to less than d days of each other.

For example, starting with and and, then

gives k so there is a probability of so at least one girl

and one boy have -birthday collisions.

The next result is based on [16] [18] [20] [38] .

Theorem 3. Consider n days in a year, a span of days, and two sets of distinctly labeled iid uniform random variables all with range: g random variables are girls and b random variables are boys. Then is the probability at least one girl and one boy have a birthday-collision and:

(10)

Proof. This proof calculates the probability of not having no boy-girl birthday collisions. That is, one minus the probability of no boy-girl birthday collisions. This gives the probability of at least one boy-girl birthday collision.

Given n days, a span, and iid uniform random variables separated into g (girls) random variables and b (boys) random variables. Then the total number unconstrained mappings of the b and g variables to is giving the denominator in front of the double sum.

The value is not impacted if either any number of boys have the same birthday or separately any number of girls have the same birthday. Rather is impacted by boy-girl collisions. Therefore, consider partitions of b boys and girls. To prevent the girls’ partitions and boys’ partitions from colliding into spans of the same range, count the number of places these i and j non-empty partitions may be mapped so there is no birthday-collision. By Lemma 1 there are

(11)

injective functions to for sets of boys and sets of girls with blocks of contiguous days with no boy or girl in them.

Now, consider placing the i and j partitions in separate locations among the function mappings to, see Naus [16] . That is, the i partitions of where each partition is in a different location and j partitions of where each partition is also in a different location by Equation (11). That is, given

and, then the product is the total number of injective

mappings of boys to i non-empty partitions and independently the number of injective

mappings of girls to j non-empty partitions.

This completes the proof.

Wash Sale Example 2: d = ±30 Calendar Days

Start with the same setup as the previous wash sale example from subsection 2.1.

Let h be half the total trades in day i. That is,. Assuming trading days and calendar days gives the probabilities of girl- boy -day birthday-collisions for a single asset type is:

Consider only a single asset type. The intuition behind these probabilities is straight- forward. For instance, consider days and to avoid boy-girl collisions each girl and boy must be separated by at least 30 days before and after their birthday from the other gender. So the 365 days may be broken into about six blocks of about 60 days.

4. Wash Sale and Integral Capital Gains and Losses

Capital gains or capital losses may be rounded to the nearest integer for US tax calculations. Provided all trades are rounded. Rounding drops the cents portion for gains whose cents portion is 50-cents or below. Rounding adds a dollar to the dollar portion of gains whose cents portion is greater than 50 cents while dropping the cents portion. Losses work the same way. Gains and losses must all be rounded or none must be rounded. So, from here on, let all gains or losses be integers.

Long term capital gains and losses are aggregated and at the same time short term capital gains and losses are aggregated. At the end of the tax year the long term and short term aggregates are added together to get the final capital gain or loss for taxation.

The focus here is capital gains or losses for capital assets that may have wash sales. Wash sales are losses, but losses may offset gains. The study of options and their associated premiums is classical [10] and we do not address it here. So, option premiums are ignored.

In a portfolio, individual capital gain values and individual capital loss values are usually distinct. Though rare, identical capital gains and capital losses are possible. Identical capital gains or losses are possible for portfolios built using options. We are ignoring option premiums. That is, asset purchases may be done via the exercise of cash-covered American-style put options. Also asset sales may be done via the exercise of American-style covered-call options. In these cases with options that become in-the-money, a portfolio manager has no control of the asset sales or purchases or timing of such trades. See Figure 1.

Most often, put or call option strike prices are at discrete increments. For example, many put and call equity options have strike prices in $5 or $10 increments. Suppose a portfolio is built only using the exercise of American-style options. Many asset gains and losses may be for identical amounts. Of course, this depends on the size of the underlying positions or the number of options written. Options with the same expiry on identically sized underlying assets may have very different values [10] .

In such option-based portfolios assume uniform, independent, and random capital gains and capital losses. This may be modeled by the Littlewood-Offord Problem.

Definition 8 is classical and extensive discussion may be found in the likes of [6] [41] . It is based directly on [4] [6] [41] .

Definition 8 (Littlewood-Offord Problem) The integer Littlewood and Offord’s problem is given an integer multi-set where and

so each is such that, for

, then what is?

Assuming equal probability of gains and losses and no drift [10] . Given an integer multi-set so. The multi-set V represents capital gains and capital losses. Capital gains and capital losses are all from sales. The iid Rademacher random variables determine if a is a capital gain or loss. All are positive since all the Rademacher variables have range, see also [5] and [40] .

Over a tax year, the total capital gain or loss is

(12)

In an optimal solution of this version of the Littlewood-Offord problem, [5] showed

the n-element multi-set has.

The next lemma’s proof follows immediately from the linearity of expectation given Rademacher random variables. See, for example, [39] .

Lemma 3. Consider any integer multi-set where and the random variable, where

, for all, then.

For any Rademacher random variable, it must be and. Since is constant. Thus, a proof of the next theorem follows since the variance of a sum of independent random variables is the sum of the variances.

Theorem 4. Consider any non-negative integer vector v and the random variable

, where, for all, then

and.

Thus, the lowest variance, , for the integer Littlewood-Offord problem occurs exactly when and. Assuming the are all Rade- macher random variables, then is maximized [6] [40] [41] as and.

Theorem 4 implies the next corollary.

Corollary 1. Assume and where

, for all, then the standard deviation of is

.

Corollary 1 highlights an exceptional case where all capital gains and capital losses are the same. Wash sales require the loss and gain to be from essentially the same security.

The generality of Theorem 4 asserts large variances too. Consider the set

, then by Theorem 4,. This last equality

follows since the sum is a geometric series.

Definition 9 (Distinct sums of a set or multi-set V) Consider a set or multi-set and let each element of the lists and be fixed values from. The two sums of V,

(13)

(14)

are distinct iff there is some, for.

Given any multi-set of positive integers, enumerate all dis- tinct sums as, for example, see Figure 2. Given any set of positive integers, where none of the distinct sums add to the same value gives.

An important observation by [5] , is that for any fixed sum s the values and differ by. Next, this observation is used to show the set has no distinct sums that add to the same value.

In particular, take any distinct sums and with associated fixed values and, respectively, for all. Suppose, for the sake of a contradiction, that. Building on Erdös’ observation, the values and may be written as where and and likewise where and, for all. Finally, the uniqueness of binary-number representations means which in turn means, for all. So, in fact, the sums and are equal, giving a contradiction.

Thus, the set satisfies the antecedent of the next theorem.

Theorem 5. Among all sets of distinct positive integers where no two distinct sums add to the same value, the set has a minimal sum .

Proof. Suppose, for the sake of a contradiction, that for some set of distinct positive integers where no two distinct sums add to the same value.

Take the next enumeration of the 2ⁿ distinct sums, , and by our supposition, and, so.

Let where sum has the list of fixed values so that, where is the vector dot pro- duct. Likewise, the sum has the list of fixed values.

The difference of any two distinct sums must be even since any fixed values and, for, are so that,

(15)

giving

(16)

which must be even.

Starting from and going to contains intervals. Since all, for, are different and their differences must be even so spans at least. That is,. This gives a contradiction of the assumption, completing the proof.

Given a set of distinct positive integers V where, Theorem 5 indicates that

. So in the case where all distinct sums of V add to different

values, erasing a wash sale loss may have a very large impact. In particular, the multi-set has largest loss, where Theorem 5 indicates

has the largest loss. In this case, when no distinct sums add to the same value, let giving

. Assuming wash sales occur with the same random and uniform probability among all losses, the expected disallowed loss is. This is

because all losses are of the form, for, and by assumption these losses all have the same probability of occurring.

Since by Lemma 3, Littlewood-Offord results are useful for under- standing likely values for. That is, gives most likely capital gains or losses outside of the expected value. None of the values in Figure 2 are 0, but if V has an even number of 1s, then the most common value is 0.

The following tail bound is given by [42] where,

(17)

(18)

(19)

Since by Theorem 4,.

Suppose and is odd. Since no sum of V is 0, there are capital gains and capital losses. This means if, then there are capital gains and capital losses. Losses are necessary for wash sales. Therefore, the bound gives the probability there are at least more gains than losses. That is, there are fewer opportunities for wash sales.

Following Figure 2, given then is the case with zero capital losses. Likewise, is the case with zero capital gains. By Lemma 3, since and, thus. Also suppose a single wash sale disallows a capital loss among all identical capital gains and losses. The single wash sale disallows a single capital loss giving the expected capital gain or loss:

(20)

The term is excluded since it has no losses, hence no wash sales.

The boy-girl birthday problem gives a necessary condition for wash sales of substantially identical securities. Recall is the probability of at least one boy-girl birthday collision, so is the probability of no such birthday collision.

Given any number of boy-girl birthday collisions of the same security and suppose these birthday collisions produce at most a single wash sale. In this case let G be a total taxable gain or loss where all gains and losses are the same. Suppose these gains and losses are all 1. This gives,

(21)

(22)

(23)

(24)

5. Conclusions and Further Directions

This paper shows the probabilistic method may be used to model some tax implications for wash sales. Variations of the birthday problem and the Littlewood-Offord problem are applied to certain tax implications of wash sales.

Modeling and simulating taxes are important in both public policy settings as well as in practical tax planning. In public policy settings, conflicting fiscal and social policies make tax rules contentious. In tax planning, unexpected events may have serious consequences. Thus, reducing certain taxes to mathematical terms gives an unusual level of percision. Such percision can only benefit public policy and tax planning.

Acknowledgements

Thanks to Noga Alon and C.-F. Lee for insightful comments.

Cite this paper

Bradford, P.G. (2016) Foundations for Wash Sales. Journal of Mathematical Finance, 6, 580-597. http://dx.doi.org/10.4236/jmf.2016.64044

References

NOTES

¹Options, like shares of stock, are fungible and there are specific option exercise assignment allocation methods used to allocate exercised options [8] .

²We used Bernoulli random variables for outcomes and we use Rademacher for outcomes.