Journal of Mathematical Finance
Vol.05 No.04(2015), Article ID:61464,11 pages
10.4236/jmf.2015.54034
Stock Price Information Content, Idiosyncratic Volatility and Expected Return
Meimei Liang
School of Finance, Shanghai University of Finance and Economics, Shanghai, China

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 21 October 2015; accepted 22 November 2015; published 25 November 2015

ABSTRACT
How idiosyncratic risks are priced in capital asset is always concerned in the financial sector. This paper theoretically analyzes the impact of idiosyncratic volatility on the expected return from the perspective of stock price’s information content, and use Chinese A-share market data, from 1994 to 2013, to do the empirical test. It finds that, if other conditions remain unchanged, when the degree of stock price information content is low, idiosyncratic volatility and expected return are negatively correlated; when the degree of stock price information content is rich, idiosyncratic volatility and expected return are positively correlated. After taking the impact of different regression methods and time spans into consideration, the conclusions are still valid, which indicates that the conclusions are robust. The reason for the above phenomenon is that idiosyncratic volatility is mainly driven by noise or information, which has different impacts on expected return.
Keywords:
Stock Information, Idiosyncratic Volatility, Expected Return, Asset Pricing

1. Introduction
How risks are priced in capital assets is always a core issue in finance. Traditional capital asset pricing model only concerns the impact of systematic risk on asset prices, omitting the impact of idiosyncratic risk. However, being restricted by the ability of funding and the ability to get access to information, it is difficult for investors to completely spread out the idiosyncratic risk. Therefore, it is necessary to analyze how idiosyncratic risks are priced.
According to Miller [1] , the existence of heterogeneous beliefs and restriction of short selling will lead to the stock’s overvaluation, since stock prices tend to reflect the optimists’ emotion. For this reason, in the existence of short selling restrictions, heterogeneous beliefs need to be considered as a pricing factor. Miller’s [1] theory implies that, when the restriction of short selling exists, there is a negative correlation between heterogeneous beliefs and expected return. There exists a positive correlation between idiosyncratic volatility and heterogeneous beliefs [2] , thus, higher idiosyncratic volatility correlates to larger heterogeneous beliefs and lower expected returns, which indicates that idiosyncratic volatility and expected return have negative correlation. Merton [3] assumes that there are no short selling restriction and no heterogeneous beliefs, but the cost to get information is very high, investors only hold stocks that they are familiar with, which makes investors not fully spread out the non-systematic risk. Thus, it requires a compensation to cover this kind of risk, which means the greater the idiosyncratic risk the higher the expected return of assets. Boehme et al. [4] believes that there are differences in the model specification between Merton [3] and Miller [1] , which makes the two conclusions different. Boehme et al. [4] introduces the assumption of short-selling restrictions in Merton’s [3] model. They found that the relationship between idiosyncratic volatility and expected return depends on the strength of short selling restrictions. In the absence of short selling restrictions, there exists a positive correlation between idiosyncratic volatility and expected return. In the condition of a complete short selling restriction, there exists a negative correlation between idiosyncratic volatility and expected return.
However, Ang et al. [5] [6] , using the data from developed countries’ markets, found a negative correlation between idiosyncratic volatility and expected return; and it could not be explained by the factors like the size of the company, book-to-market ratio, momentum, liquidity, company’s financial leverage, trading volume, turnover, spreads, co-skewness, or the degree of difference in analysts’ predictions. In addition, developed countries obtained relatively well-established short selling mechanism, it could not be reasonably explained from the above theory, then it was called “the idiosyncratic volatility mystery”. After that, lots of scholars began to look for the explanation of “the idiosyncratic volatility mystery”, but they had not reached a consensus yet.
Fu et al. [7] and other scholars, using the data of different markets and different time spans, empirically illustrated the relationship between idiosyncratic volatility and expected rate of return; they found a positive correlation between the two and believed that the so-called “idiosyncratic volatility mystery “does not exist”. Bali and Cakici [8] found that the frequency of data used to estimate the idiosyncratic volatility, the weights used to calculate portfolios’ rate of return, the number of stocks in each stock portfolio, the size of company, the liquidity and other indicators would affect the estimation results, so that the conclusion of Ang et al. [5] was not robust. Jiang et al. [9] explained “the idiosyncratic volatility mystery” from the perspective of heterogeneous beliefs, they believed that the difference in investors’ expectation about companies with poor profitability in the future would lead to greater transaction volume and higher idiosyncratic volatility; after taking control of the profitability, the relationship between idiosyncratic volatility and cross-sectional rate of return became not significant. Huang et al. [10] examined “the idiosyncratic volatility mystery” proposed by the Ang et al. [5] , and found that “the idiosyncratic volatility mystery” was mainly caused by the reverse effect of the rate of return.
In summary, there have not formed a consensus in the pricing of idiosyncratic risk in capital assets pricing, neither theoretically nor empirically; and the researches on “the idiosyncratic volatility mystery” are still relatively active. The main contribution of this paper is that it considered from fresh perspective of information’s content, and built a theoretical model to analyze how idiosyncratic volatility affected expected return, and then it used the data from 1994 to 2013 of Chinese A-share market to test empirically.
2. Theoretical Model
This paper is based on theoretical model of Lee and Liu [11] and also do further analysis; in consideration of paper’s length limitation and its readability, this paper will first show the hypotheses and the main conclusions in Lee and Liu’s [11] model (more details of derivation can be visible originally), then do further theoretical derivation, then obtain this paper’s conclusion.
Lee and Liu [11] assume that, there exists risk free assets and N + 1 risky assets on the market, risky assets 1 to N are individual stocks, risky asset N + 1 is market index, all of the assets exists for periods of T, the liquidity value of assets n in T period is:
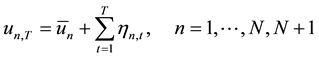 (1)
(1)
where  is the expected value of liquidity of asset n,
is the expected value of liquidity of asset n, 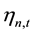 is a shock to the asset value of n at the period t. In addition, Lee and Liu [11] assume that there exist three types of traders in the market: the noise trader; the discretionary type trader; the informed trader. In the period of t, the noise traders do not know
is a shock to the asset value of n at the period t. In addition, Lee and Liu [11] assume that there exist three types of traders in the market: the noise trader; the discretionary type trader; the informed trader. In the period of t, the noise traders do not know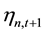 , their demand for assets is exogenous; it does not depend on the real value of the assets. Noise trader’s total demand for assets
, their demand for assets is exogenous; it does not depend on the real value of the assets. Noise trader’s total demand for assets  is
is ,
, 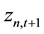 meets the following distribution:
meets the following distribution:
 . (2)
. (2)
Same as the noise trader, the discretionary type trader does not know the value of 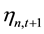 at the period of time t. Every discretionary type trader can choose to continue as uninformed or choose to become informed trader by making noise signals, but it requires some certain costs. In particular, the value of
at the period of time t. Every discretionary type trader can choose to continue as uninformed or choose to become informed trader by making noise signals, but it requires some certain costs. In particular, the value of  can be decomposed into two parts:
can be decomposed into two parts:
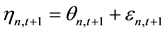 . (3)
. (3)
Among them, 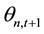 and
and 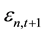 are independent of each other, they are subject to the following distributions:
are independent of each other, they are subject to the following distributions:
 (4)
(4)
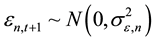 . (5)
. (5)
By making noise signals at the time period of t, the discretionary trader can observe the value of 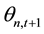
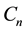

where a represents risk aversion coefficient, 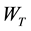
Suppose the investor j owns 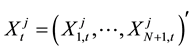
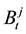
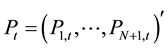
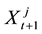
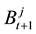
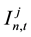
From the above model assumptions that the stock yield can be obtained:
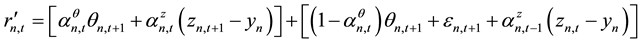
where 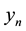
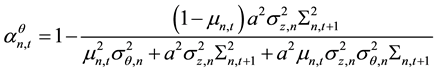

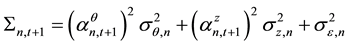
Stock price information content is:
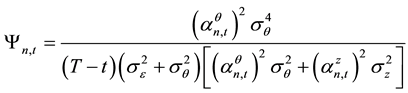
On this basis, the main conclusions on Lee and Liu’s [11] paper are (herein referred to as the conclusions: 1) the values of parameters that made the idiosyncratic volatility increases with the increase of stock
price information content do not exist, that is, there is no parameters that made 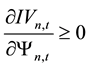
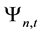
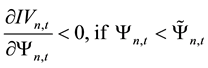
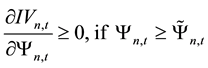

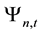
The above are model’s assumptions and main conclusions from Lee and Liu’s [11] paper, then, based on it, this paper goes for further analyses. First, by the Formula (7) we find the first derivative of the stock’s expected rate of return with respect to the number of informed traders:
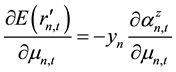
among them,
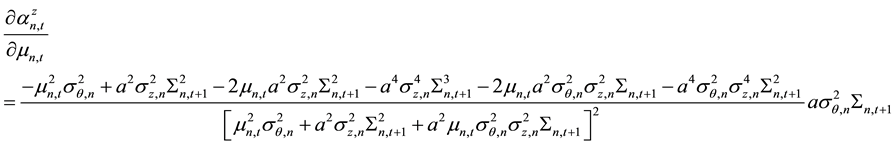
Next, the paper will first analyze the positive or negative of the derivative of the stock’s expected rate of return with respect to the number of informed traders, so as to determine the impact of the number of informed traders to the stock’s expected rate of return. Since Lee & Liu (2011) [11] assumed that investor are not extremely risk-averse, and the degree of risk aversion meets,
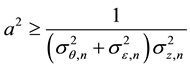
And because

there
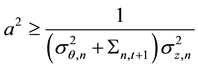
so
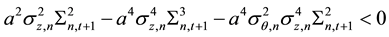
then

Taking Formula (12) and Formula (18) together it can be obtained that,
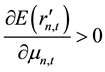
From the above, the derivative of stock’s expected rate of return with respect to the number of informed traders is positive, which indicates that the number of informed traders yields a positive impact on stock’s expected rate of return. Next, the paper will analyze the impact of the number of informed traders to the information content of the stock. By Lee and Liu’s (2011) [11] conclusion, the expression of stock price information content is:

Let,
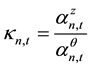
the derivative of stock price information content with respect to the amount of informed trading is:

Because,
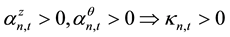
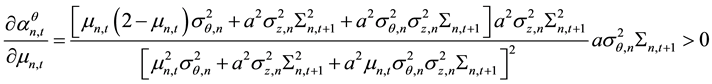
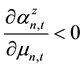
so,

then,
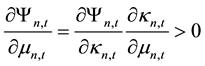
Whereby, the derivative of stock price information content with respect to the number of informed traders is positive, which means that the larger the number of informed traders the richer degree of information content the stock has. Next it will analyze the derivative of stock’s expected rate to return with respect to the information content of the stocks, so as to analyze how the degree of information content of stocks impact on its expected rate of return. According to the chain rules we can obtain,
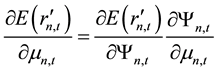
Combining (19) with (27) it can be obtained,
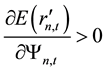
Hence, the derivative of stock’s expected rate of return with respect to stock price information content is positive, which indicates that stock price information content has a positive impact on stock’s expected rate of return, which means that the richer the degree of information content of stock price the higher the expected rate of return. Next the paper will demonstrate the relationship between idiosyncratic volatility and stock’s expected rate of return on the basis above.
According to Equation (19) and the chain rule it can be obtained that,
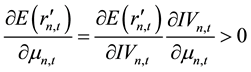
For this reason, the sign of 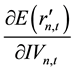
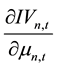
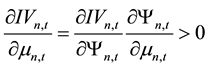
For this reason, 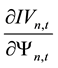
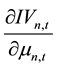

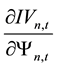
on the stock’s expected rate of return and the impact of stock price information content are the same, and both are subject to the effect of the information content of the stock. Taking Lee and Liu’s [11] conclusions on the relationship of stock price information content and idiosyncratic volatility together, the paper can get to the following relationship between stock’s expected rate of return and idiosyncratic volatility: 1) there does not exist parameters that made expected rate of return increase as the idiosyncratic volatility increases, which means that
there are no parameters that make
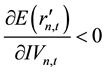


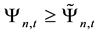
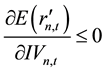

3. Sample Data Selection and Empirical Methods
3.1. Sample Data Selection
The paper takes Chinese A-share listed companies stock’s data and financial data, from 1994 to 2013, and filters it based on the following principles: 1) excluding financial and insurance companies; 2) excluding the ones with trading day less than 120; 3) excluding abnormal data, such as the data of market value less than or equal to zero; 4) excluding the ones missing important variables, such as the lack of market capitalization, profits etc. Therefore, the size of the sample is 18,004; in order to exclude the impact from extreme variables the paper deal with all the variables based on 1% of winsorize.
All the data this paper use are from CSMAR (China Stock Market Accounting Research) database.
3.2. Variable Measurement
1) Idiosyncratic volatility. Similar to Lee and Liu’s [11] method, this paper use daily data for each stock each year to perform Fama and French’s 3-factor model, then using one to minus the coefficient of determination from the regression, thereby it measures the stock’s idiosyncratic volatility of this year. Specific regression equation is as follows:
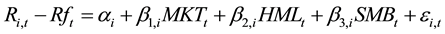
where 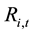
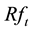
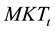
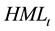

2) Stock price information content.
Price reaction measurement measures the degree of influence on stock price from a certain amount of investor’s transaction. When other conditions remain unchanged, the larger the price reaction measurement, then the larger shock to the stock price from the certain stock transaction and indicate the weaker the stock’s liquidity is. Whereas, when the stock pricing is much more efficient, the stock will have much well liquidity. Thus, While the stock price more efficient, better liquidity, therefore, can take the opposite number of the stock price reaction to measure the degree of information content [11] . According to the method adopted by Amihud [12] , divided the absolute value of daily return by daily trading volume (one hundred million Yuan for the unit),making logarithm adjustment, then taking average of such result, finally taking the opposite number of it; what we get is the price reaction measurement for that year. Specific calculation is as follows:

where 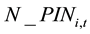
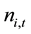
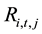
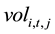
However, the larger the company size, the smaller the idiosyncratic volatility, and the much more unstable the company’s profit, the larger the idiosyncratic volatility. But all these are not caused by the change in the stock price information content, to this end, in the study these two variables need to be controlled. Similar to Lee and Liu’s [11] , this paper takes the opposite number of price responsiveness on company size and company earnings volatility regression, and the resulting residual is regarded as share price information content which has a direct impact on the idiosyncratic volatility, denoted as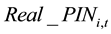
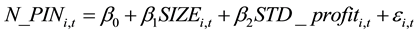
where 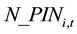

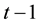
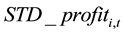
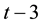
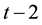
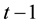
3.3. Empirical Methods
In this paper, three groups are arranged each year according to the one-year lagged stock information content, where, G = 1 represents the lowest degree of information content of the stock price; G = 2 represents the moderate degree of information content of the stock price; G = 3 represents the richest degree of information content of the stock price. For the different information content stock groups, the paper analyzes the relationship between idiosyncratic volatility and stock’s expected rate of return respectively; the regression model used is as follows:
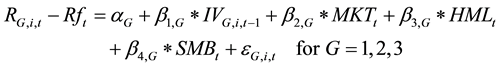
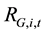
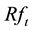



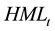
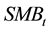
4. Empirical Results
4.1. Descriptive Statistics
Table 1 shows the descriptive statistics for the variables of this paper, you can see, the average of idiosyncratic volatility is 0.551, which indicates that 3-factor pricing model holds a overall explanatory power of less than 50% in our country’s stock pricing, therefore, it is quite necessary to consider the effect of non-systematic risk into pricing.
4.2. The Impact of Stock Price Information Content on Idiosyncratic Volatility
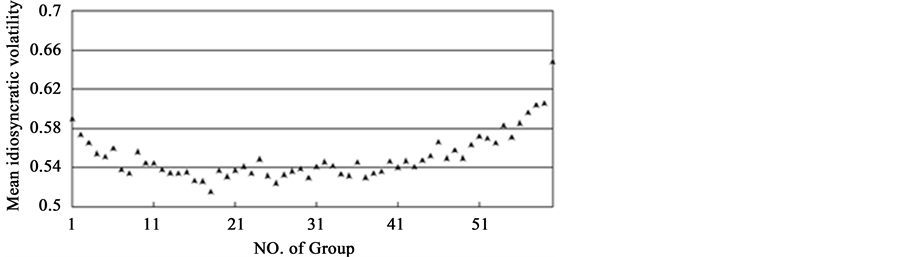
According to the theoretical analysis of this paper, the paper first needs to examine whether idiosyncratic volatility and stock price information content present a U-shaped relationship in our country. Despite that there have scholars verified the U-shaped relationship between the two by using China’s A-share data [13] , the data range and variables’ measurement methods used herein are different from it, it is necessary to make a test in this paper. Firstly, according to the degree of stock price information content the stocks are divided into 60 groups every year; the larger the group number the richer the degree of stock price information content. Then calculate the average of the idiosyncratic volatility of the 60 groups, and let group number is the x axis and idiosyncratic volatility be y axis, drawing a scatter plot, specifically shown in Figure 1. As can be seen from Figure 1, the average of idiosyncratic volatility decreases, as the degree of stock price information content gets richer (before Group 20), and then be stable (Group 21 to Group 40), finally rising (after Group 20), indicating that idiosyncratic volatility and stock price information content may present U-shaped relationship.
Table 2 shows the fama-macbeth regression results of idiosyncratic volatility to the stock price information content. G = 1 (2, 3) represents the regression results obtained from the use of the former 20 groups’ stock price information content (Group 21 to Group 40, Group 41 to Group 60). From Table 2 it can be found that, when G = 1, the coefficient of stock price information content is −0.0438, be significant at the 1% critical point; when G
Table 1. Descriptive statistics.
Figure 1. A scatter plot of the mean value and stock price information content group.
Table 2. Regression analysis of idiosyncratic volatility and stock price information content.
Note: The value of t statistics in parentheses, *, **, *** denote p < 0.1, p < 0.05, p < 0.01.
= 2, the coefficient of stock price information content is 0.0128, but not significant; when G = 3 the coefficient of stock price information content is 0.0888, be significant at the 1% critical point. This suggests that as the degree of stock price information content gets higher the idiosyncratic volatility first increases then decreases presenting U-shaped relationship between the two, which are in line with the conclusions of the theoretical model.
4.3. The Impact of Stock Price Information Content on the Rate of Return
Table 3 presents the regression results of the stock’s rate of return to the stock price information content. It can be seen from Table 3 that no matter what type of regression methods the coefficients of stock price information content are all positive and are significant at the 1% critical point. It demonstrates that the richer the degree of stock price information content, the general investors need higher risk compensation when the amount of informed traders gets larger.
4.4. Stock Price Information Content, Idiosyncratic Volatility and Stock’s Expected Rate of Return
Followed the method of Ang et al.’s (2006, 2009), using the one-year lagged idiosyncratic volatility (denoted as L_IV) as expected idiosyncratic volatility. Acquiring Fama-macbeth cross-section regression method, for the various degree of lagged stock price information content, regress stock’s rate of returns on one-year lagged idiosyncratic volatility, the specific regression results are shown in Table 4. From Table 4 it can be found that, when the one-year lagged stock price information content is very low (G = 1), the coefficient of lagged idiosyncratic volatility is −0.197 and it is significant at the 5% critical point; when the lagged stock price information content is very rich (G = 3), the coefficient of lagged idiosyncratic volatility is 0.325 and it is significant at the 1% critical point. This suggests that, when the stock price information content is very low, the impact of idiosyncratic volatility on expected rate of return is negative, while when the stock price information content is very rich, the impact of idiosyncratic volatility on expected rate of return is positive, and it is consistent with the paper’s theoretical conclusion.
4.5. Robustness Test
Ang et al. (2006, 2009), using the time span of January, March, June, December’s data respectively to analyze the relationship between idiosyncratic volatility and expected rate of return to verify that time span does not
Table 3. Regression results of rate of returns to stock price information content.
Note: Regression (4), WKT, HML and SMB are the corresponding coefficients of market factor, value factor and size factor, the same below. Value of t statistics in parentheses, *, **, *** denote p < 0.1, p < 0.05, p < 0.01.
Table 4. Regression results of stock returns to one-period lagged idiosyncratic volatility.
Note: The value of t statistics in parentheses, *, **, *** denote p < 0.1, p < 0.05, p < 0.01.
have significant impact on the relationship between idiosyncratic volatility and expected rate of return. Therefore, the paper taking January, March, June as the time span do the analysis, it found that changing the time span does not have significant impact on the above conclusions.
Some scholars believe that, compared to three-factor model, multi-factor model can examine the impact of various factors on the dependent variable directly (Han Liyan et al., 2008), drawing on their idea, this paper will include book-to-market ratio, company capitalization and market excess returns rate as the control variables into the regression model, the results are the same as the empirical results, which indicates that changing the regression model does not influence the paper’s conclusions.
5. Conclusions
This paper, based on Chinese A-share market data and from the perspective of stock price information content, analyzes how idiosyncratic volatility impact on the stock’s expected rate of return both theoretically and empirically. It was found that, if other conditions remain unchanged, when the degree of stock price information content is rich, the idiosyncratic volatility and the stock’s expected rate return have a positive correlation; when the degree of stock price information content is low, such correlation is negative. This paper holds that, when the degree of stock price information content is rich, idiosyncratic volatility is mainly driven by information; so the richer the degree of stock price information content, the greater the idiosyncratic volatility, the more informed traders. The more involvement of informed traders makes the asymmetric information risk that general investors faced with get larger, which will require more risk compensation, hence higher expected rate of return for stocks. Taking different time spans and regression models into consideration, we find the above conclusions are still valid, hence, the conclusions are robust.
The paper theoretically analyzes how the stock price information content effects on idiosyncratic volatility then impact on stock’s expected rate of return, in addition it tests empirically; it provides a fresh perspective for the study of “the mystery of idiosyncratic volatility”, which has a relatively strong academic meaning.
Acknowledgements
This research is supported by NSSF (13 ECJL032).
Cite this paper
MeimeiLiang, (2015) Stock Price Information Content, Idiosyncratic Volatility and Expected Return. Journal of Mathematical Finance,05,401-411. doi: 10.4236/jmf.2015.54034
References
- 1. Miller, E.M. (1977) Risk, Uncertainty, and Divergence of Opinion. Journal of Finance, 32, 1151-1168.
http://dx.doi.org/10.1111/j.1540-6261.1977.tb03317.x - 2. Rajgopal, S. and Venkatachalam, M. (2011) Financial Reporting Quality and Idiosyncratic Return Volatility. Journal of Accounting and Economics, 51, 1-20.
http://dx.doi.org/10.1016/j.jacceco.2010.06.001 - 3. Merton, R.C. (1987) Presidential Address: A Simple Model of Capital Market Equilibrium with Incomplete Information. Journal of Finance, 42, 483-510.
http://dx.doi.org/10.1111/j.1540-6261.1987.tb04565.x - 4. Boehme, R.D., Danielsen, B.R. and Kumar, P. (2009) Idiosyncratic Risk and the Cross-Section of Stock Returns: Merton (1987) Meets Miller (1977). Journal of Financial Markets, 12, 438-468.
http://dx.doi.org/10.1016/j.finmar.2009.01.004 - 5. Ang, A., Hodrick, R., Xing, Y. and Zhang, X. (2006) The Cross-Section of Volatility and Expected Returns. Journal of Finance, 61, 259-299.
http://dx.doi.org/10.1111/j.1540-6261.2006.00836.x - 6. Ang, A., Hodrick, R., Xing, Y. and Zhang, X. (2009) High Idiosyncratic Volatility and Low Returns: International and Further U.S. Evidence. Journal of Finance Economics, 91, 1-23.
- 7. Fu, F. (2009) Idiosyncratic Risk and the Cross-Section of Expected Stock Returns. Journal of Financial Economics, 91, 24-37.
http://dx.doi.org/10.1016/j.jfineco.2008.02.003 - 8. Bali, T.G. and Cakici, N. (2008) Idiosyncratic Volatility and the Cross Section of Expected Returns. Journal of Financial and Quantitative Analysis, 43, 29-58.
- 9. Jiang, G.J., Xu, D. and Yao, T. (2009) The Information Content of Idiosyncratic Volatility. Journal of Financial and Quantitative Analysis, 44, 1-28.
http://dx.doi.org/10.1017/S0022109009090073 - 10. Huang, W., Liu, Q., Rhee, S.G. and Zhang, L. (2010) Return Reversals, Idiosyncratic Risk and Expected Returns. Review of Financial Studies, 23, 147-168.
http://dx.doi.org/10.1093/rfs/hhp015 - 11. Lee, D.W. and Liu, M.H. (2011) Does More Information in Stock Price Lead to Greater or Smaller Idiosyncratic Return Volatility. Journal of Banking and Finance, 35, 1563-1580.
- 12. Amihud, Y. (2002) Illiquidity and Stock Returns: Cross-Section and Time-Series Effects. Journal of Financial Markets, 5, 31-56.
http://dx.doi.org/10.1016/S1386-4181(01)00024-6 - 13. Zhang, Y.R. and Li, X.Y. (2010) R2 and Stock Price Information. Journal of Management Science, 13, 17-28.