Journal of Mathematical Finance
Vol.05 No.02(2015), Article ID:56252,14 pages
10.4236/jmf.2015.52015
Optimal Investment under Dual Risk Model and Markov Modulated Financial Market
Lin Xu, Liming Zhang, Dongjin Zhu
School of Mathematics and Computer science, Anhui Normal University, Wuhu, China
Email: xulinahnu@gmail.com, zlmiac@yahoo.com, djzhu@mail.ahnu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 October 2015; accepted 30 April 2015; published 12 May 2015
ABSTRACT
In this paper, the optimal investment problem for an agent with dual risk model is studied. The financial market is assumed to be a diffusion process with the coefficients modulated by an external process, which is specified by the solution to a kind of stochastic differential equation. The object of the agent is to maximize the expected utility from terminal wealth. Together with the regularity property of the value function, by dynamic programming principle, the value function of our control problem is turned to be the unique solution to the associated Hamilton-Jacob-Bellman (HJB for short) equation. When the utility is an exponential function with constant risk aversion, close form expressions for value function and optimal investment policy are obtained.
Keywords:
Optimal Investment, Dual Risk Model, Markov Modulated Model, HJB Equation

1. Introduction
The classical surplus process of an insurer is given by
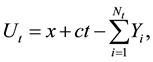 (1)
(1)
where x > 0 is the initial surplus, c is the positive constant premium income rate, Nt is Poisson process with parameter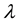 , which denotes the total number of claims up to time t. Denote the time of arrival of the ith claim by Ti and the size of the ith claim by Yi. More details about the surplus process can be found in Asmussen and Albrecher [1] , Rolski et al. [2] . As pointed out by Albrecher et al. [3] , its dual process may also be relevant for companies whose inherent business involves a constant flow of expenses while revenues arrive occasionally due to some contingent events (e.g. discoveries, sales). For instance, pharmaceutical or petroleum companies are prime examples of companies for which it is reasonable to model their surplus process as
, which denotes the total number of claims up to time t. Denote the time of arrival of the ith claim by Ti and the size of the ith claim by Yi. More details about the surplus process can be found in Asmussen and Albrecher [1] , Rolski et al. [2] . As pointed out by Albrecher et al. [3] , its dual process may also be relevant for companies whose inherent business involves a constant flow of expenses while revenues arrive occasionally due to some contingent events (e.g. discoveries, sales). For instance, pharmaceutical or petroleum companies are prime examples of companies for which it is reasonable to model their surplus process as
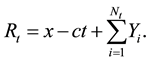 (2)
(2)
The past decade has witnessed an increasing attention on the research of dual risk model. For example, see Albrecher et al. [3] for optimal dividend problem, see Cheung and Drekic [4] for dividend approximation and dual risk model with perturbation, see Yao et al. [5] for optimal dividend and equity issuance, see Zhu and Yang [6] for ruin probability under a Markov modulated dual risk model.
As we all know, investment is an important element in the financial agent for which can bring them potential profit. Thus, optimal investment for insurers has drawn great attentions in recent years, for example, see the works of Bai and Guo [7] , Browne [8] , Fleming and Hernández [9] , Hipp and Plum [10] , Li et al. [11] , Zhang and Siu et al. [12] . However, to our best knowledge, there are few papers concentrate on the optimal investment of agent with dual risk process. This is the main contributions of this paper.
Usually, the coefficients of the dynamics of the financial market are assumed to be constant. However, in reality, the returns from the risky assets might not be constants. So, it would be of practical relevance and importance to consider asset pricing models with non-constant coefficients, which can incorporate the feature of non- stationary returns. Among all kinds of stochastic coefficients models, Markov-modulated risky model has been recognized recently as an important feature to asset price models. There is much literature documenting such models in assets returns, such as French et al. [13] . Meanwhile, since Markov-modulated risky model contains several very important stochastic volatility models, thus can be seen as an explanation of many well-known empirical findings, such as the volatility smile, the volatility clustering, and the heavy-tailed nature of return distributions (c.f. Fleming and Hernández [9] , Pham [14] , Zariphopoulou [15] [16] , and references therein). In this paper, the optimal investment problem of an agent with dual risk process under the Markov modulated financial market is studied. By dynamic programming principle, we obtained the HJB equations satisfied by the value function and finished the corresponding verification theorem. A solid example is presented to illustrate how to solve the HJB equation when the claims are exponential distribution. This rest of this paper is organized as follows. In Section 2, the model and problem are introduced. The HJB equation associated with our control problem and the verification theorem for optimal control are investigated in Section 3. In Section 4, we focus on the exponential utility function and closed form expression for optimal investment is obtained. In Section 5, we listed the highlights of this paper and conclusions from the results.
2. Formulation of the Problem
Let 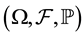 be a complete probability space which carries all random variables to appear in this paper. To proceed our discussion, we introduce the following variables and notations. Let
be a complete probability space which carries all random variables to appear in this paper. To proceed our discussion, we introduce the following variables and notations. Let 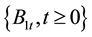 and
and  are two standard Brownian motions, which describe the perturbations of the insurer and the financial market and
are two standard Brownian motions, which describe the perturbations of the insurer and the financial market and  is the augmented filtration generated by aforementioned stochastic process, i.e.
is the augmented filtration generated by aforementioned stochastic process, i.e.
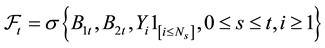
and satisfying the usual conditions. For simplicity,  ,
,  ,
,  and
and  are assumed to be mutually independent.
are assumed to be mutually independent.
Assume that there are two kinds of asset available for investors, one risky asset and one risk free asset. The risky asset is assumed to be
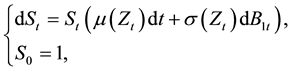 (2.1)
(2.1)
where ,
,  are the stochastic investment return rate and volatility of the risky market respectively. The dynamic of the external factor is specified by the solution to the following stochastic differential equation (SDE for short)
are the stochastic investment return rate and volatility of the risky market respectively. The dynamic of the external factor is specified by the solution to the following stochastic differential equation (SDE for short)
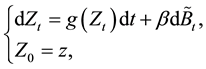 (2.2)
(2.2)
where




where 



where 

with the convention that
Definition 1 We say that the strategy 
1) The strategies Kt has to be measurable and predictable with respect to the filtration
2) There is a constant CK which may depend on the strategies K such that
We denote the set of admissible strategies as
Suppose that the company is interested in maximizing the expected utility of wealth at time T. Without loss of generality, we can define the utility function 



We say that an admissible combined strategies 
Hypothesis 1 1) The functions


2) The function 


3. Properties of Value Function and the Verification Theorem
In this section we embed the problem of maximizing the expected utility from terminal wealth on a finite horizon 

with terminal condition
The following verification theorem shows that under some proper conditions, a solution to previous HJB equation provides us the optimal investment policy.
Theorem 2 (The Verification Theorem) Suppose that there is a smooth solution 




Then for each
Suppose further that there exist two bounded measurable functions

then 
Proof. Let

where 

Compensate (3.5) by
we have

Assumptions (3.3) and (3.4) mean that
are martingales. Assumption (2.8) implies that
is a martingale. Then, by taking the expectation on both sides of (2.11) yields that

Note that f is a smooth solution to HJB equation (2.6), we have
That is to say for any

Taking 

The proof of the second part of this theorem follows in a similar manner. If we plug 


By taking the supremum over all 
By considering (2.13) for all
Letting 
Moreover, by recalling (2.14), it is easy to find that
This completes the proof.
Remark 1 Classical method of applying HJB equation for solving optimal control problems is pre-assume (or find) that there exist a smooth solution to the HJB equation, and then finish the argument by verification theorem. However, the HJB equations do not always admit classical solution, and thus the verification theorem invalid. In this case, viscosity solution will be introduced to cover the connections between the optimal control problem and the HJB equation. However, in next section, we exploit a closed representation of the solution to the HJB Equation (3.1) when the utility function is an exponential type. By this results, we further find the closed from optimal investment policy and the expressions of value function. As to very general utility function, it is difficult to find closed form solutions to HJB equation and we leave it as future research.
4. Existence of a Optimal Pair of Solutions under the Exponential Utility Function
In this section, we devote to the existence and uniqueness of the solution of the HJB Equation (3.1) when the preferences of the insurer are exponential, i.e., the utility function is governed by

In order to get a linear PDE, in the remainder of this paper we consider only the case where the correlation coefficient is equal to zero
Hypothesis 2 1) 
2) g is uniformly Lipschitz and bounded;
3) 
Considering the form of the utility function, We speculate the following function as a solution to the HJB Equation (3.1)

where 






Plugging these partial derivatives of f into the HJB Equation (3.1), we obtain

For simplicity of presentation let us introduce the following notation
It is trivial to see that the supremum is achieved at
Indeed, by a measurable selection theorem, we may find a pair of bounded progressively measurable processes 


The following theorem asserts the existence and uniqueness of aforementioned Cauchy equation (4.9).
Theorem 3 Assume that

Then the Cauchy problem given by (4.9) has a unique solution, which satisfies the following conditions:


where C1 and C2 are constants.
Proof. The theorem will be proved if we can show that the Cauchy problem given by (4.9) satisfies the conditions of the Theorem A.1. So we just need to check them.
・ Since 

・ Considering Hypothesis 2, we know immediately that 
・ Now we show that
is bounded and uniformly Hölder continuous in compact subsets of
In fact, by Hypothesis 2, it is clear that the first term of 


Thus 


Noting that 




For the second term of


Then 




Then by the mean value theorem of bivariate functions, we know that there is 
where 




By (4.10), we obtain that 



Since the Cauchy problem (4.9) is homogeneous with a constant terminal condition, then the right-hand side of (4.9) satisfies the property of linear growth and continuous. Finally, the conditions of Theorem A.1, it is easy to find that the Cauchy problem (4.9) has a unique solution 
The aim of the next theorem is to relate the value function V in the form (4.2) to the HJB Equation (3.1) in the form of the Cauchy problem (4.9).
Theorem 4 If (4.10) are satisfied, then the value function defined by (2.5) has the form:
where 
then the investment strategy 

and
Proof. We have already verified that
is a smooth solution of the HJB Equation (3.1). To prove that 

Firstly, we consider the case in which



In the last line, we used 


We find that
In the last inequality, we used Hölder inequality (


where C is a positive constant. Moreover, by the Minkovski inequality
(


i.e., 

One should note that
and
Recall that K is a pair of admissible strategy, by Hölder inequality, we have
Since 
This indicates that

and
Evidently, (3.3) and (3.4) are easily seen to hold with




By 


This case is dealt with the same arguments by suitable modification to the first part of the proof. First, we get
and
To accomplish the proof, it is sufficient to prove that

Note that
and the fact that 

Similarly, since K is a pair of admissible strategy and 
This completes the proof.
5. Highlights and Summary
The main contributions of this paper include:
・ Both stochastic coefficients financial model and dual risk model are taken into account.
・ Rigorous proof of verification theorem for optimal policy is provided and closed form expressions for optimal policies and value function are derived.
・ A solid example is presented to illustrate how to solve the HJB equation.
As a result, we find that the optimal investment policy is a function of the state of the external Modulate Markov process. When there is no modulated process, the model considered in this paper is reduced to the optimal investment problem under the risky market with stationary coefficient and our results cover those existing results (see Bai and Guo [7] or Li et al. [11] ). One should note that when the coefficients are not sensitivity to the changes of the external Markov process, i.e. when the external Markov process changes, the coefficients of the risky market do not oscillate greatly, then our optimal investment policies seem to be very conservative because the optimal investment amount is near to a constant.
Acknowledgements
The authors are very grateful to anonymous referees’ detailed comments and suggestions, which makes this paper much better. Lin Xu would like to acknowledge the support of the National Natural Science Foundation of China (Grant No. 11201006). Zhu Dongjin would like to acknowledge the support of Major Projects of Colleges and Universities in Anhui Province Natural Science Foundation (KJ2012ZD01).
References
- Asmussen, S. and Albrecher, H. (2010) Ruin Probabilities. World Scientific, Singapore. http://dx.doi.org/10.1142/9789814282536
- Rolski, T., Schmidli, H., Schmidt V. and Teugels, J. (2009) Stochastic Processes for Insurance and Finance. John Wiley & Sons, Hoboken.
- Albrecher, H., Badescu, A. and Landriault, D. (2008) On the Dual Risk Model with Tax Payments. Insurance: Mathematics and Economics, 42, 1086-1094. http://dx.doi.org/10.1016/j.insmatheco.2008.02.001
- Cheung, E.C.K. and Drekic, S. (2008) Dividend Moments in the Dual Risk Model: Exact and Approximate Approaches. Astin Bulletin, 38, 399-422. http://dx.doi.org/10.2143/AST.38.2.2033347
- Yao, D.J., Yang, H.L. and Wang, R.M. (2010) Optimal Financing and Dividend Strategies in a Dual Model with Proportional costs. Journal of Industrial and Management Optimization, 6, 761-777. http://dx.doi.org/10.3934/jimo.2010.6.761
- Zhu, J.X. and Yang, H.L. (2008) Ruin Probabilities of a Dual Markov―Modulated Risk Model. Communications in Statistics―Theory and Methods, 37, 3298-3307. http://dx.doi.org/10.1080/03610920802117080
- Bai, L.H. and Guo, J.Y. (2008) Optimal Proportional Reinsurance and Investment with Multiple Risky Assets and No- Shorting Constraint. Insurance: Mathematics and Economics, 42, 968-975. http://dx.doi.org/10.1016/j.insmatheco.2007.11.002
- Browne, S. (1995) Optimal Investment Policies for a Firm with a Random Risk Process: Exponential Utility and Minimizing the Probability of Ruin. Mathematics of Operations Research, 20, 937-958. http://dx.doi.org/10.1287/moor.20.4.937
- Fleming, W.H. and Hernández, D. (2005) The Tradeoff between Consumption and Investment in Incomplete Financial Markets. Applied Mathematics and Optimization, 52, 219-235. http://dx.doi.org/10.1007/s00245-005-0826-1
- Hipp, C. and Plum, M. (2000) Optimal Investment for Insurers. Insurance: Mathematics and Economics, 27, 215-228. http://dx.doi.org/10.1016/S0167-6687(00)00049-4
- Li, Z.F., Zeng, Y. and Lai, Y.Z. (2012) Optimal Time-Consistent Investment and Reinsurance Strategies for Insurers under Heston’s SV Model. Insurance: Mathematics and Economics, 51, 191-203. http://dx.doi.org/10.1016/j.insmatheco.2011.09.002
- Zhang, X. and Siu, T.K. (2009) Optimal Investment and Reinsurance of an Insurer with Model Uncertainty. Insurance: Mathematics and Economics, 45, 81-88. http://dx.doi.org/10.1016/j.insmatheco.2009.04.001
- French, W.E., Schwert, G.W. and Stambaugh, R.F. (1987) Expected Stock Returns and Volatility. Journal of Financial Economics, 19, 3-29. http://dx.doi.org/10.1016/0304-405X(87)90026-2
- Pham, H. (2002) Smooth Solutions to Optimal Investment Models with Stochastic Volatilities and Portfolio Constraints. Applied Mathematics and Optimization, 46, 55-78. http://dx.doi.org/10.1007/s00245-002-0735-5
- Zariphopoulou, T. (1999) Optimal Investment and Consumption Models with Nonlinear Stock Dynamics. Mathematical Methods of Operations Research, 50, 271-296. http://dx.doi.org/10.1007/s001860050098
- Zariphopoulou, T. (2001) A Solution Approach to Valuation with Unhedgeable Risks. Finance and Stochastics, 5, 61-82. http://dx.doi.org/10.1007/PL00000040
Appendix. Parabolic Partial Differential Equations
To illuminate the expression of our research problem, now we introduce and summarize some important results on parabolic PDEs, which play a key role in the proof of Theorem 4.1 (existence and uniqueness theorem), and some terminology and definitions are introduced. We believe that this work will be useful in the development of this paper.
Definition 5 Let
1) We say that E is uniformly elliptic, if there is 
for all 
2) A function f on 




3) f is said to be uniformly Hölder continuous in 


Theorem A.1 (Friedman, 1975). We consider the following Cauchy problem:

where L is given by
If the Cauchy problem (A.1) satisfies the following conditions:
1) The coefficients of L are uniformly elliptic;
2) The functions 



3) The functions 


4) The function 



5) The function 


6) The function 




Lemma A.1 Let f be a real positive bounded function with bounded derivative, then f is uniformly Hölder continuous with exponent
Proof. By the mean value theorem and using that 
where K is a constant. By f is positive,we have
i.e.
The proof of this Lemma is now complete.
Theorem A.2 (Pham, 1998). Let 
with a standard Brownian motion Bs. We assume that for some

for all










































































