Journal of Mathematical Finance
Vol.4 No.4(2014), Article
ID:49339,7
pages
DOI:10.4236/jmf.2014.44026
Extending Multi-Period Pluto and Tasche PD Calibration Model Using Mode LRDF Approach
Denis Surzhko
Credit Risk Modeling Unit, OJSC VTB Bank, Moscow, Russia
Email: densur@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2014; revised 15 July 2014; accepted 3 August 2014
ABSTRACT
The intention of this paper is to propose extension to the Pluto and Tasche PD calibration model for low default portfolios that could produce more stable LRDF estimates and eliminate the necessity of quartile choice, while preserving adequate level of conservatism. Multi-period Pluto and Tasche model allows us to fulfill Basel committee requirements regarding long-term LRDF calibration even for portfolios with no observable defaults. The main drawback of that approach is a very strict requirement for the sample: only borrowers that are observable to the bank within each point on long-term horizon could be used as observations. Information regarding rating migrations, borrowers that arrived in the portfolio after sample cutoff date and borrowers that left the portfolio before the end of long-term calibration horizon should be excluded from the sample. Proposed Mode approach pairs Pluto and Tasche model with mode LRDF estimator (proposed by Canadian OSFI), as the results, it eliminates drawbacks of the original Pluto and Tasche model.
Keywords:Credit Risk, Low Default Portfolio, PD Calibration

1. Introduction
This paper is dedicated to ultra-low default portfolios. Ultra-low default portfolio is the portfolio for which we haven’t got enough historical defaults to estimate discriminatory power of the ranking model (e.g. calculate Gini coefficient) and/or central tendency. Therefore it’s impossible to perform classical central tendency probability of default (PD) calibration using one of the common approaches described, for example, in Tasche (2009) [1] . Nevertheless, using Pluto and Tasche (2005) [2] model it is possible to statistically calibrate PD for ultra-low default portfolios even in case of absence of historical defaults.
The idea of Pluto and Tasche approach is the following (details see in Pluto K. and Tasche D. (2005) [2] ). We assume that PD assigned to rating classes (still to be estimated) reflects the decreasing credit-worthiness of the grades, i.e. PD is a non-decreasing function of rating class:
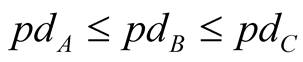 . (1)
. (1)
The most prudent assumption of PD for any given rating is its equality to the PD of the worst rating within the rating grade. Therefore, we assume  for rating class A,
for rating class A, 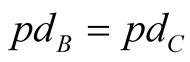 for B rating and so forth. Assuming unconditional independence of the default events, the probability of observing no defaults turns out to be
for B rating and so forth. Assuming unconditional independence of the default events, the probability of observing no defaults turns out to be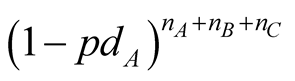 , where
, where 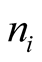 denotes number of borrowers in the rating class i. In order to find PD estimate for rating class A, we should solve the following inequality (given some confidence level
denotes number of borrowers in the rating class i. In order to find PD estimate for rating class A, we should solve the following inequality (given some confidence level 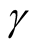 for
for 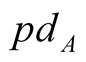 estimation):
estimation):
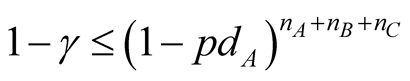 . (2)
. (2)
In case of available 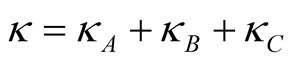 (number of defaults should be less or equal to the number of borrowers in each rating class:
(number of defaults should be less or equal to the number of borrowers in each rating class: ) historical defaults we simply replace probability estimate by the CDF (cumulative distribution function) of binomial distribution:
) historical defaults we simply replace probability estimate by the CDF (cumulative distribution function) of binomial distribution:
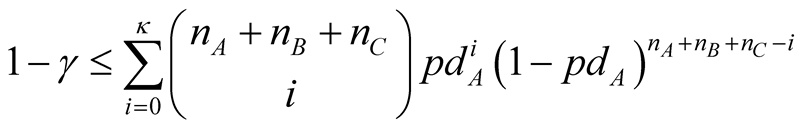 (3)
(3)
Using the same logic we could estimate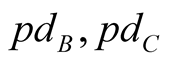 :
:
 (4)
(4)
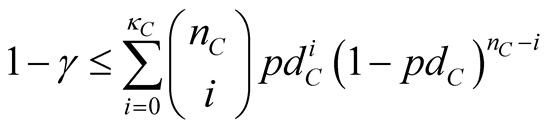 . (5)
. (5)
Generalized rule for PD calibration that is used under original P&T model that could be expressed as:
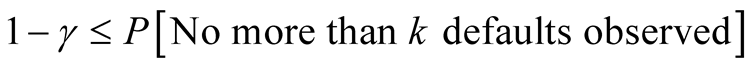 (6)
(6)
As the result, solving (6) for each separately leads us to original P&T one-period PD calibration approach that obviously don’t comply with Basel committee requirement for long-term LRPD estimation period [3] . In order to comply with the requirements, one can use pooling, e.g. replacing the one-year number of borrowers in a grade with the sum of the borrower numbers of this grade over the years (analogously for the numbers of defaulted borrowers). However, when turning to the case of cross-sectionally and intertemporally correlated default events, pooling does not allow for an adequate modelling—there is no way to incorporate into the model information about correlation between borrowers and autocorrelation of the systemic factor. Other option is to use multi-period extension of the Pluto and Tasche (P&T) model which takes into account correlation between borrowers and autocorrelation of the systemic factor.
Multi-period P&T model assumes (as in Vasicek, Oldrich A. (1997) [4] ) that a default of borrower is triggered if the change in a value of its assets results in a value lower than some default threshold :
:
 (7)
(7)
where 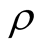 stands for the so-called asset correlation,
stands for the so-called asset correlation, 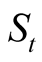 is the realization of the systematic factor in year t, and
is the realization of the systematic factor in year t, and 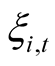 denotes the idiosyncratic (or borrower-specific) component of the change in value. The cross-sectional dependence of the default events stems from the presence of the systematic factor
denotes the idiosyncratic (or borrower-specific) component of the change in value. The cross-sectional dependence of the default events stems from the presence of the systematic factor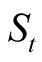 . Both systematic and idiosyncratic factors are standard normally distributed, and idiosyncratic factors are i.i.d., while joint distribution of
. Both systematic and idiosyncratic factors are standard normally distributed, and idiosyncratic factors are i.i.d., while joint distribution of 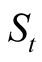 is completely determined by the correlation matrix RC (which could be expressed using time-distance function).
is completely determined by the correlation matrix RC (which could be expressed using time-distance function).
Borrower i’s default occurs in year t if:
 (8)where default threshold
(8)where default threshold 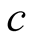 could be calibrated from unconditional PD:
could be calibrated from unconditional PD:
 (9)
(9)
with 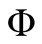 denoting the standard normal distribution function.
denoting the standard normal distribution function.
Following Bluhm, C., Overbeck, L. and C. Wagner (2003) [5] , conditional on particular systematic factor realization default probability in a given year could be expressed as the following link function:
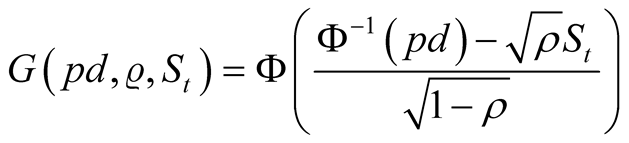 (10)
(10)
From (7), (8) and by using of the conditional independence of the 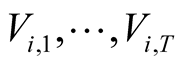 and given systematic factors
and given systematic factors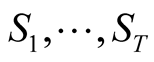 , we obtain:
, we obtain:
 (11)
(11)
Right hand side of (6) could be written as:
 (12)
(12)
Solving inequality (6) in each rating class separately for PD values given Equation (12) leads us to PD estimates according to original multi-period Pluto & Tasche model.
Above described P&T model has obvious drawbacks in case of multi-period calibration. Pooling approach is unable to take into account correlation between borrowers and systematic factor time series, as the result, we get PD estimates that has zero sensitivity to really observable economic effect of default clusterization.
Multi-period P&T model considers only the borrowers that were present at the beginning of the observation period. Therefore we lose significant amount of information for stable portfolios and decreasing stability of PD estimates. Moreover, in case of shifts in the portfolio (like significant growth of the portfolio or high prepayment rate) the model is totally inapplicable.
The other drawback of P&T model is the necessity of the quartile  choice. Mode
choice. Mode  could be seen as not enough conservative value (could underestimate true LRDF in more than 50% cases—see Monte Carlo simulation results below). Current practices of quartile choice relate to external factors such as external ratings, CDS spreads and so on. Those practices are suitable for quartile choice under ICAAP, but a PD value of the borrower is an objective figure that obviously should not vary between banks and depend on risk profile of a lender.
could be seen as not enough conservative value (could underestimate true LRDF in more than 50% cases—see Monte Carlo simulation results below). Current practices of quartile choice relate to external factors such as external ratings, CDS spreads and so on. Those practices are suitable for quartile choice under ICAAP, but a PD value of the borrower is an objective figure that obviously should not vary between banks and depend on risk profile of a lender.
2. P&T Model Extension Using Mode Calibration
The idea of the proposed approach is to pair P&T model with the approach proposed by Canadian financial institutions regulator, the Office of the Superintendent of Financial Institutions (OSFI), as a possible way to increase conservatism of LRPD estimation. For detail illustrations, please refer to OSFI document: “Risk Quantification of IRB Systems at IRB Banks” [6] and Miu P. and Ozdemir B. (2008) [7] .
The idea of the approach is to find the 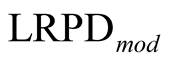 given the average long-term default rate in a given rating class as:
given the average long-term default rate in a given rating class as:
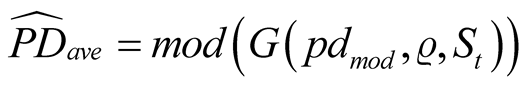 (13)
(13)
where mod (•) is the mode of the distribution of the average default rate given the arguments of the link function (4). Since there is no explicit analytical Equation to relate the mode of the distribution with the underlying LRPD, this approach involves changing the assumed value of LRPD until we obtain a mode (through simulations) of the distribution of the simulated average default rate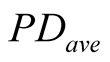 , which is identical (or close enough) to the observed average default rate average
, which is identical (or close enough) to the observed average default rate average .
.
Proposed approach consists of the following steps (assuming we have historical data for T periods in R rating classes, for each period—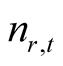 borrowers and
borrowers and 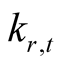 defaults):
defaults):
1) Apply to each historical period  one-period P&T model (1) with the quartile
one-period P&T model (1) with the quartile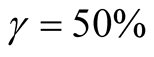 . The output of the model is a set of one period PDs:
. The output of the model is a set of one period PDs: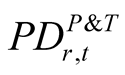 ;
;
2) Let’s assume that 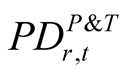 is a true default rate within period t in rating class r (instead of observed default rate which could be distorted due to LDP nature of the portfolio);
is a true default rate within period t in rating class r (instead of observed default rate which could be distorted due to LDP nature of the portfolio);
3) Apply OSFI 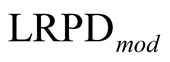 approach to
approach to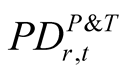 .
.
a) Calculate mean of P&T default rates in each rating class:
 (14)
(14)
b) Simulate 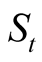 using normal multivariate distribution with correlation matrix RC for
using normal multivariate distribution with correlation matrix RC for 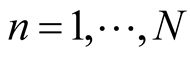 scenarios.
scenarios.
c) For each rating class R find such  that satisfies Equation:
that satisfies Equation:
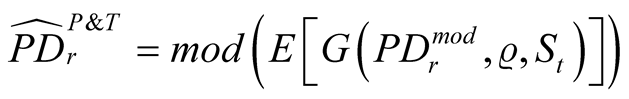 , (15)
, (15)
where expectation is taken with respect to scenarios.
Equation (15) provides us with the values of 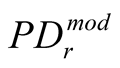 that correspond to claimed Mode LRDF calibration approach. In order to prove the efficiency of the proposed estimator we could use Monte-Carlo simulations.
that correspond to claimed Mode LRDF calibration approach. In order to prove the efficiency of the proposed estimator we could use Monte-Carlo simulations.
3. Monte-Carlo Simulation Details
All examples are based on the portfolio with 3 rating classes A, B, C with the number of borrowers for the first portfolio: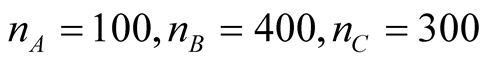 ; second portfolio:
; second portfolio: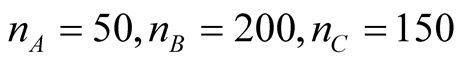 . One-factor model crosssectional correlation is constant
. One-factor model crosssectional correlation is constant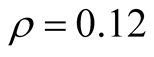 , while intertemporal correlation, described by correlation matrix RC, depends on time distance:
, while intertemporal correlation, described by correlation matrix RC, depends on time distance:
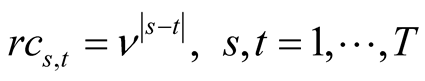 (16)
(16)
where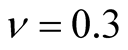 , number of periods T is 5 (as required by [3] ).
, number of periods T is 5 (as required by [3] ).
In order to simulate the loss of information in multi-period P&T model random repayment events are incorporated into the simulations. Each borrower in each period could leave the portfolio due to debt repayment with the probability P [repayment]. Simulations were held with two different values: 15% and 30%. We assume that the bank is keen to hold stable rating structure, i.e. in case of default or repayment, the borrower is replaced by another one in the same rating class. Therefore in case of the Proposed Mode approach we have the same rating structure at the beginning of each period.
True LRDF rates (PD variables values in Equation (10)) by rating classes are: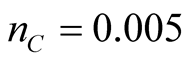
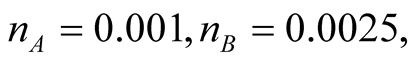 .
.
1) Monte-Carlo simulation schema (applied for each combination of the repayment probability and portfolio) is the following:
a) Generate 1000 portfolio scenarios, in each scenario;
b) Generate 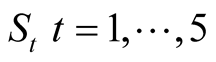 values using correlation matrix (16);
values using correlation matrix (16);
c) Test each borrower for default case (using its rating LRDF value and link function (10));
d) Simulate repayments with the uniform probability P [repayment];
i) Produce two types of tables (number of borrowers and defaults) by rating classesii) Taking into account repayments, not taking into account default replacements (multi-period P&T model).
2) Under assumption of stable rating structure—all repaid and defaulted borrowers are replaces in the next period (pooled P&T model, Proposed Mode based approach):
a) Estimate LRDF values using the following approaches;
b) P&T with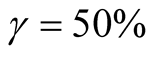 ;
;
c) P&T with ;
;
d) Proposed Mode based approach.
e) Pooled P&T model.
3) For each approach calculate the following statistics:
a) Mean of LRDF estimates;
b) Standard deviation of LRDF estimates;
c) Percentage of LRDF underestimations;
d) Plot LRDF estimates density (using build-in «R» function «density» for kernel).
Simulation results for different combinations of prepayment rates and portfolios are provided in Tables 1-4. LRDF estimates density graphs are provided in the Figures 1-4.

Figure 1. Portfolio: (50, 200, 150); Repayment probability = 15%.

Figure 2. Portfolio: (50, 200, 150); Repayment probability = 30%.

Figure 3. Portfolio: (100, 400, 300); Repayment probability = 15%.

Figure 4. Portfolio: (100, 400, 300); Repayment probability = 30%.
In all cases Proposed Mode approach is more conservative than multi-period P&T 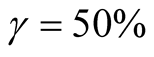 model and Pooling approach and less conservative than multi-period P&T
model and Pooling approach and less conservative than multi-period P&T . The maximum LRDF underestimation rate for Mode approach is less than 30%, therefore the approach is enough conservative and there is no need in additional parameters involvement (in terms of max LRDF underestimation rate Mode approach is almost twice more conservative than P&T
. The maximum LRDF underestimation rate for Mode approach is less than 30%, therefore the approach is enough conservative and there is no need in additional parameters involvement (in terms of max LRDF underestimation rate Mode approach is almost twice more conservative than P&T 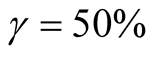 model and Pooling).
model and Pooling).
The standard deviations of the estimates is on par with multi-period P&T 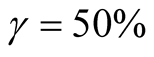 model and Pooling approach, at the same time Mode approach SD is significantly smaller than multi-period P&T
model and Pooling approach, at the same time Mode approach SD is significantly smaller than multi-period P&T 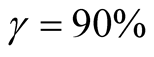 SD. As the result, additional conservatism in the Mode approach does not lead to decreasing in the stability of the estimates.
SD. As the result, additional conservatism in the Mode approach does not lead to decreasing in the stability of the estimates.
Increase in repayment probability leads to shift in mean of PD estimates and increased SD for multi-period P&T models (despite there is no economic reason to increasing PD due to increase in repayment rates). Obviously, it’s due to significant sample restrictions. Proposed Mode approach has not got such restriction, as the result, both mean and standard deviations of estimates are stable despite repayment rate changes.
4. Conclusions
The Proposed Mode approach has the following advantages:
1) It takes into account all available information about borrowers and defaults in comparison to serious sample constrains of multi-period P&T model. As the result, estimates don’t depend on the repayment profile of the portfolio: increase in repayments does not lead to negative changes in standard deviation of the results and shifts in PD values.
2) It takes into account cross-sectional and intertemporal correlation structure (see steps 3. b and 3. c in Monte Carlo simulation schemas) that leads to more accurate and theoretically justified LRDF estimates.
3) It provide enough level of conservatism (the approach is a much more conservative approach than pooled and one-period P&T model γ = 50%) while maintaining the same of standard deviation of estimates, therefore there is no need to use additional quartile parameter in order to increase conservatism.
4) Additional conservatism of the approach does not lead to increase in standard deviation values as it happens in case of increased quartile in P&T model.
References
- Tasche, D. (2009) Estimating Discriminatory Power and PD Curves When the Number of Defaults Is Small. Working Paper
- Pluto, K. and Tasche, D. (2005) Thinking Positively. Risk, August, 72-78.
- Basel Committee on Banking Supervision (BCBS) (2004) Basel II: International Convergence of Capital Measurement and Capital Standards: A Revised Framework. http://www.bis.org/publ/bcbs107.htm
- Vasicek, O.A. (1997) The Loan Loss Distribution. Technical Report, KMV Corporation, San Francisco.
- Bluhm, C., Overbeck, L. and Wagner, C. (2003) An Introduction to Credit Risk Modeling. Chapman & Hall/CRC, Boca Raton
- Office of the Superintendent of Financial Institutions (OSFI) of Canada (2004) Risk Quantification of IRB Systems at IRB Banks: Appendix—A Conservative Estimate of a Long-Term Average PD by a Hypothetical Bank. December 2004.
- Miu, P. and Ozdemir, B. (2008) Estimating and Validating Long-Run Probability of Default with Respect to Basel II Requirements. Journal of Risk Model Validation, 2, 1-39.


