Open Journal of Marine Science
Vol.05 No.01(2015), Article ID:53131,17 pages
10.4236/ojms.2015.51008
Overview of Tide Characteristics in Cameroon Coastal Areas Using Recent Observations
R. Onguene1,2,3*, E. Pemha4, F. Lyard2, Y. Du-Penhoat2, G. Nkoue5, T. Duhaut3, E. Njeugna1, P. Marsaleix3, R. Mbiake1, S. Jombe6, D. Allain2
1Multidisciplinary Climate Change Research Laboratory, University of Douala, Douala, Cameroon
2LEGOS/OMP UMR 5566 (CNES-CNRS-IRD-UPS), Toulouse, France
3Laboratoire d’Aérologie, CNRS and Toulouse University, Toulouse, France
4Laboratory of Applied Mechanics and Hydraulic, Faculty of science, University of Yaounde I, Yaounde, Cameroon
5Faculty of Science, University of Douala, Douala, Cameroon
6DOUALA Harbour, Douala, Cameroon
Email: *ziongra@yahoo.fr, portdouala@iccnet2000.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 November 2014; revised 28 November 2014; accepted 7 December 2014
ABSTRACT
Time series of sea level heights have been collected at different stations along the Cameroon coast. The dataset covers a period ranging from 2007 to 2012. Tide data measured by float type recorders have been digitalized and quality-controlled with tools developed at Laboratoire d’Etudes Géo- physique et Océanographie Spatiale (LEGOS). Short gaps in the data have been interpolated while large gaps were not. Tide constituents were retrieved through harmonic analysis using 123 waves having a period ranging from long ones to eighth-diurnal ones. The reconstructed signal is used to assess the quality of both the data and the analysis and the erroneous records were examined and corrected. The effect of the hourly averaging of the raw data on the quality of the analysis is also investigated. The tide constituents having the largest amplitudes are, as expected, the semi-diur- nal, diurnal, fourth-diurnal and long term constituents. The major components of semi-diurnal waves are the M2 and S2 tides. The M2 tide height ranges between 0.5 and 0.85 m. The maximum height is found at Cameroon estuary and the minimum at the Kribi station located in the South coast. The S2 constituent varies similarly as the M2 constituent. Its amplitude ranges between 0.18 and 0.52 m. The lowest S2 amplitude occurs also at Kribi station. In the Dibamba estuary the spectrum shows a larger number of significant semi-diurnal and fourth-diurnal waves than other zones. Concerning diurnal waves, the dominant one is the K1 tide and its amplitude is homogeneous along the coast. The influence of the long-term components is the strongest in the Cameroon estuary due to important fluctuations of the rivers run-off.
Keywords:
Tide, Cameroon Coast, Harmonic Analysis, Prediction

1. Introduction
The Cameroon coast is a zone where important industrial and environmental interests are located. Cameroon, as its neighbouring countries, is an important offshore oil and gas producer. The Cameroon government also in- vests in important marine projects like the industrial Kribi harbour complex and the marine protected areas of Kribi-Campo and Mouanko. Moreover, the country faces other problems in coastal areas like salinity intrusion and sediment transport increase in Cameroon estuary, which are probably linked to climate change [1] . All these issues led to an increasing interest in the understanding of the local coastal dynamics and especially tides.
Geographically, the coast of Cameroon is connected to the equatorial Atlantic Ocean. The shoreline spreads over 400 km (8.3˚E - 10.15˚E and 3.3˚N - 5˚N) (Figure 1) between Idenau and Campo. The littoral zone pre- sents an array of varying geomorphological attributes consisting of creeks, lagoons, sand and rocky beaches, coastal plains, wetlands and mangroves [2] . These varying landforms include the Cameroon estuary which has the particularity to be a vast delta where three important rivers join. The tides of the Cameroon coast have been described by many authors but little attention has been given to the tide components. Most of these studies are very descriptive. [3] shows that tides are meso-tidal with the maximum tidal range of 3 m. According to [4] [5] tides in Cameroon estuary are semi-diurnal and very asymmetric.
The signal variations in the Kribi zone suggest that the diurnal constituents are higher in this region. In the Cameroon estuary, and more specifically in the Dibamba and Wouri estuaries, an investigation realized by [6] shows that the tide amplification depends mostly on convergence shapes. However, none of these studies pre- sents a harmonic analysis of tide data. This paper aims to investigate the tidal constituents using the harmonic analysis method in the Cameroon coastal areas in order to perform a tide prediction.
The data in this region is scarce and not homogeneously distributed. The research collaboration between the University of Douala, Douala harbour and LEGOS in France has allowed creating a database including all the
Figure 1. Map of the Cameroonian coast. The red points in the figure correspond to the location of the stations listed in Table 1.
different observation networks. Some locations are better surveyed than others. The Wouri estuary (SM2 and SM4 in Figure 1), for example has many tide gauges. In the north-west of the Cameroon coast (Limbe, SM SONARA), in the south (Kribi-Campo, SM KRIBI) and in Japoma water station in Dibamba (SMD), few measurements have been taken between 2007 and 2010. In all cases, the minimum duration of the recorded time series is six months. This period corresponds to the minimum duration required to perform an accurate harmonic analysis [7] . The paper is organized as follows: Section 2 presents the database. Section 3 addresses the harmonic analysis and prediction methods. Section 4 presents the resulting tidal constituents for the Cameroon coast and the related prediction. Section 5 focused on discussion and concludes paper.
2. Observations
2.1. Materials
The tide gauges installed in Cameroon use different technologies and measuring processes. A float type recorder using an analogue technology has been installed in Japoma water station in the Dibamba estuary (SMD in Figure 1).
The device consists of a float on a lever arm connected to a recorder (Figure 2(a)) and uses a still well to re-
Figure 2. Tide gauge sensors installed in the Cameroonian coast: (a) Float type recorder (stations SM2, SM4, SMD) with analogue recorder; (b) Float type recorder (stations SM2, SM4) with digital recorder; (c) Radar sensor tide gauge (SM SONARA); (d) Pressure sensor installed on the bottom in the coastal water close to Kribi habour.
duce the effects of waves and wind. This type of sensor has also been installed at stations SM2 and SM4 (Figure 1) in the Wouri estuary.
The other tide gauge operate using numerical recorders and have two different measuring processes. The first process records the pressure at a fixed depth (for example on the bottom) and converts it to an equivalent sea level using the hydrostatic equation. The pressure sensor deployed in the Cameroon estuary is shown in Figure 2(b). Raw data are sampled at 4 Hz and data logged as average over burst. Burst length is selectable between 1 to 60 seconds. This sensor is connected to a radio transmitter that communicates with a radio receiver connected to a computer. This model is installed at SM2 and SM4 stations (Figure 1). Figure 2(d) shows the one installed at Kribi during the period running from November 2009 to June 2010 (SM Kribi, see Figure 1). The last type is a very accurate radar sensor tide gauge (Figure 2(c)). This tidal gauge is part of the Global Sea Level Observing System network (GLOSS). It is installed at the SONARA refinery. This tide gauge is referenced in Figure 1 by SM SONARA.
2.2. The Tide Dataset
The tide datasets used in this study covers the period 2007-2012. The years and the durations of the records are varying for each station. Table 1 summarizes the positions of the tide gauges, the names of the stations, their characteristics and the measurement periods. In order to reduce the size of the dataset, the values are averaged over time. For Kribi and Limbe the data are sampled every fifteen minutes. For SM2 and SM4, the data are given every minute. Analogue tide gauge records at SM2, SM4 and SMD stations have been sampled manually with the time interval of 60 minutes. The data time series in the SMD station is short (eight months from January to August 2007) and includes large period of missing data, therefore the analysis derived from the measurements of this station is not very accurate.
3. Harmonic Analysis and Prediction Method
In order to provide the tide harmonic constants for the 5 stations along the Cameroon coast a tool developed at LEGOS laboratory has been used (for details on this tool, refer to ftp://ftp.legos.obs-mip.fr/pub/ecola/tools/ttb.pdf). The aim of harmonic analysis is to obtain significant and stable parameters describing the tidal regime at the place of observation [8] . This method is based on the assumption that the tidal variations can be represented by a finite number
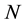 of harmonic terms having the form:
of harmonic terms having the form:
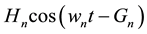 (1)
(1)
where
 is the amplitude,
is the amplitude,
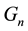 the phase lag defined using as a reference the tide phase at Greenwich, and
the phase lag defined using as a reference the tide phase at Greenwich, and
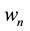 the angular speed. Harmonic constants are the solution of the following system expressed under its complex form, only applicable in case of the Darwin convention, described in Schureman (1940: pp. 74-79).
the angular speed. Harmonic constants are the solution of the following system expressed under its complex form, only applicable in case of the Darwin convention, described in Schureman (1940: pp. 74-79).
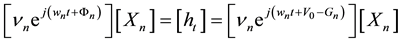 (2)
(2)
where
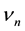 is a complex number giving the nodal correction in amplitude and phase,
is a complex number giving the nodal correction in amplitude and phase,
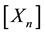 the harmonic coefficient vector linked to the gauge point,
the harmonic coefficient vector linked to the gauge point,
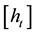 the time series vector,
the time series vector,
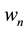 the astronomic pulsation of the wave,
the astronomic pulsation of the wave,
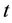 the time,
the time,
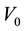 the equilibrium argument at the time zero.
the equilibrium argument at the time zero.
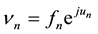 (3)
(3)
where
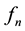 is the nodal factor and
is the nodal factor and

Table 1. Location and characteristics of the tide stations.
Taking

the solution is given by doing a standard least square fit by multiplying both sides with the transposed matrix of harmonic vectors

When time series are shorter than 1 year, we used the admittance method developed by Cartwright et al., 1980, which stipulates that the oceans and seas have a fairly smooth response. This means that the ratio of the amplitude over the astronomic potential of astronomic waves can be interpolated from their neighbours. This is useful when the length the data does not allow separating two constituents, which makes the matrix


where


If the length of the data does not allow some components to be separated,


According to [7] - [9] , the prediction of the sea level at time



where


The amplitude of the diurnal and semi-diurnal tide is modulation by slow variations associated with longer period motions of the Earth, Moon, and Sun [8] - [12] . These inter-annual tide modulation effects have been observed with two extensively documented signals (the 18.61-year lunar nodal cycle and the 8.85-year cycle of lunar perigee, see [13] - [16] .
4. Results
4.1. Tide Constituents
The International Hydrographic Organisation (IHO) and Service Hydrographique et Océanographique de la Marine (SHOM) recommend the use of 500 waves to guarantee the quality of tidal predictions (see, e.g., http://www.iho.int/mtg_docs/com_wg/IHOTC/IHOTC_Misc/TWLWG_Constituent_list.pdf). However, the duration of the time series analysed here limits the number of tidal constituents that can be retrieved. Therefore the harmonic analysis method use in this study computes only 75 waves for the oceanic stations and 123 waves for the estuarine stations. This limits the spectrum to the eighth-diurnal period, which is sufficient in our framework because the amplitudes of waves having a shorter period are lower than 1 mm.
The amplitude and phase for each wave is computed for all stations and the results of the analysis for each station are presented in Figure 3. Table 3 gives the tide constituents for waves having amplitude greater that 5 mm for each station. The tide constituents having the largest amplitudes are, as expected, the semi-diurnal, di- urnal, fourth-diurnal and long term constituents. The results show that the tidal constituents in the Cameroon
Table 2. Principle astronomical harmonic components according to [7] - [11] .
Table 3. Tide constituents (amplitude and phase lag) for each station. Only waves with amplitude higher than 5 mm are shown. The phase lag is ranged between −180 and 180 deg.
Figure 3. Amplitude spectrum of tide for the five stations whose location is given in Figure 1.
coast are moderated with average amplitude of the M2 tide equal to 0.5 m over the continental slope. This confirms the results of the tide atlas build by [6] . The tide is amplified in the shallow water of estuaries and its peak is observed in the Wouri (SM4) and Dibamba (SMD) estuaries because of the strong convergence of these bays. The minimum is observed at the Kribi station located in the South coast. Over all the stations, the M2 tide amplitude ranges between 0.5 and 0.85 m.
The S2 constituent varies similarly as the M2 constituent. Its amplitude ranges between 0.18 and 0.52 m. The lowest S2 amplitude occurs also at Kribi station and the maximum occurs in Cameroon estuary. At the Japoma water station, in addition to the classic M2 and S2 components, the spectrum shows a large number of semi-di- urnal waves (ST2, 2N2 SNK2, Nu2, R2, LA2, T2 and MSN2) with amplitude higher than 0.1 m (Figure 3). This explains the larger tide amplitude observed in this location compared to other stations despite relatively smaller M2 and S2 amplitudes. The major diurnal wave in the Cameroon coast is the K1 tide with an amplitude of the order of 0.14 m and its amplitude is homogeneous along the coast.
The fourth-diurnal waves are amplified in the estuary. In this group, the M4 tide is the major component. Figure 3 shows that the amplitudes of the fourth-diurnal waves in the estuary stations (SM4 and SMD) are higher than the ones of the stations located in the continental slope (SM2, SM-Kribi and SM-SONARA). Figure 3 also shows that long-term components (Sa, Ssa, Msm and Msf) at the SMD station have a higher amplitude than other stations. As shown in Figure 1, this station is located upstream in the Dibamba river, therefore this result can be explained by the strong fluctuations of the river run-off and non-linear interactions between M2 and S2 tides occurring in shallow waters. For example, the amplitude of the Msf tide that is due to these non- linear effects is equal to 0.14 m and therefore not negligible.
Comparatively, in coastal zones out of estuaries the amplitudes of the lunar-solar fortnightly Msf (corresponding to a 14.765 day period) and the lunar fortnightly Mf (corresponding to a 13.661 day period) is of the order of 1 cm. However, as explained above, the harmonic analysis of the data collected at the SMD station needs to be confirmed with longer records.
4.2. The Effect of the Hourly Averaging
Usually the harmonic analysis method is applied to hourly data. However, in estuaries, the high frequency constituents of tide (above the fourth-dirunal constituent) have an important amplitude (see the previous section).
Therefore the use of hourly average data may introduce a non negligible error in the analysis compared to using the raw data sampled at a 1mn time interval. This problem may affect the SM2, SM4 and SMD station in the Cameroon estuary.
In order to investigate the impact of the hourly average, the harmonic analysis is performed on two datasets collected at the SM2 and SM4 stations equipped with a numerical recorder. The SM2 dataset corresponds to the raw data sampled at a 1mn time interval and the second corresponds to the hourly average of these raw data. Figure 4 and Figure 5 show the differences of the tide constituents amplitude and phase between the two sample periods for the two stations. The amplitude difference is of the order of 1 cm for major waves. However, at the SM2 station, the R2 and T2 tide amplitudes present significant differences, respectively equal to 0.16 and 0.14 m, which were not expected. The scatter plot presented in Figure 4(a) also shows that there is a non negligible phase shift between the two datasets at SM2 station. These differences indicate that the quality of the SM2 data are questionable, which will be discussed in the next section. As to the SM4 data, the amplitude difference is very small over all the frequencies and the scatter plot presented in Figure 5(a) shows that the phase shift is not significant, except for a few waves.
Despite the fact that the SM4 station is located upstream in the Wouri estuary and that, as a consequence, its spectrum exhibit important high frequency harmonics, the results obtained with the hourly SM4 data are comparable to those obtained with a 1mn sampling interval. This suggests that we can provide an accurate harmonic analysis using hourly data even in the estuaries, which allows collecting longer time series due to the limited memory required to store this type of data.
4.3. Prediction of Tides
The quality of the tide constituents obtained by harmonic analysis is evaluated by reconstructing the tidal signal and comparing it to the data. The prediction of tides is realized with a tool developed at LEGOS (for details on this tool, refer to ftp://ftp.legos.obs-mip.fr/pub/ecola/tools/ttb.pdf). The results are satisfactory for the SM- SONARA, SM-Kribi and SM4 stations (Figure 6). The observed tide and the predicted tide are perfectly in phase and the difference between the two signals is a residual noise. The amplitude of these differences can be up to 0.2 m at low and high tides.
However, Figure 6(a) shows that the prediction is not accurate for the SM2 station operated by the Douala harbour. The amplitude of the difference between the predicted tide and the data reaches 0.5 m at low and high tides. The residual clearly includes an important part of the dominant components, which implies that the harmonic analysis does not correctly extract the tide for this station. This problem had already been noticed in the previous section where the amplitude of the R2 and T2 constituents for this station was found to be ten times greater than the ones of the others stations. These values are therefore unrealistic and can be the cause of the high prediction error.
One of the typical problems in the observation of tides is due to a shift of the reference time. Figure 7 indeed
Figure 4. Comparison between the harmonic analysis results computed with data sampled at 1 minute and data averaged at a 1h time scale at the station SM2. The scatter plot (a) gives the phase for the 1 h averaged data as a function of the phase for raw data for each constituent. The spectrum (b) shows the constituents amplitudes for 1h averaged data (red), raw data (blue) and their differences (green).
shows several time shifts in the dataset measured at the SM2 station. We need to fix in order to recompute the tide constituents. To investigate this hypothesis, the time derivative of the sea surface height was computed in order to locate sudden jumps in the data, which is possible because the tide involves only slow changes of height. This analysis is presented in Figure 7 which shows that the peaks in the time derivative correspond very well to the errors in data. Five major anomalies were detected and were found to be an increase or a decrease of one hour in the reference time. These anomalies always occur in the first day or last day of the month, which sug- gests that they could be caused by the operator during maintenance activities. After correction of these spurious jumps, the T2 and R2 tides constituents fell down to 1.5 and 0.2 cm respectively. The M2 amplitude also in- creases from 0.71 to 0.75 m and its phase from 135.46˚ to 149.1˚. Table 4 shows the corrected major tides constituents for the SM2 station. As expected, the amplitude of the corrected residual is consequently reduced (see Figure 8).
Figure 5. Comparison between the harmonic analysis results computed with data sampled at 1 minute and data averaged at a 1 h time scale at the station SM4. The scatter plot (a) gives the phase for the 1 h averaged data as a function of the phase for raw data for each constituent; The spectrum (b) shows the constituents amplitudes for 1 h averaged data (red), raw data (blue) and their differences (green).


Figure 6. Observed tide (green curve), predicted tide (red curve) and residual (blue curve) as a function of time in julian day at: (a) SM2 station; (b) SM4 station; (c) SM SONARA station; (d) SM Kribi station.





Figure 7. Tidal height measured at the SM2 station (in meter, red curve) and time derivative (in cm∙s−1, green curve) for various days (a); (b); (c); (d) and (e).
Table 4. Tide constituents (amplitude and phase lag) for SM2 station with corrected data. Only waves with amplitude higher than 5 mm are shown. The phase lag is ranged between −180 and 180 deg.
Figure 8. Observed tide (green curve), predicted tide (red curve) and residual (blue curve) as a function of time in julian day at the SM2 station after correction of the spurious jumps.
5. Discussion and Conclusion
Harmonic analysis allows extracting the tidal constituents and predicting the sea level height. However, this method does not extract perfectly all the amplitude of the tide constituents. As can be seen in Figure 6 and Figure 8, the residuals still include both low and high frequencies. A Demerliac filter can be applied to remove the low frequency signal from the residuals [17] . The difference between the residuals and the filtered signal can be added to the prediction of the tide.
This correction can have great interest for sea surface height data assimilation and adjustment of numerical tidal model that require high quality tide predictions. The remaining high frequencies of the residuals are more difficult to analyse because one part is due to the atmospheric forcing and another to the tidal forcing.
The records used in this study are not long enough to allow the very long-term constituents to be retrieved with harmonic analysis. For example, the lunar nodal, nodal sub-harmonic, lunar perigean, and perigean sub- harmonic cycles (corresponding to 18.6, 9.3, 8.85, and 4.4-year signals respectively [18] [19] ) cannot be obtained. Moreover, the diurnal and semi-diurnal tides are modulated over a large range of time scales including annual and inter-annual variations [20] and these cycles constituents requires dedicated techniques to be retrieved.
Although harmonic analysis combined with the admittance method shows accurate results with relatively short time series, these results are less reliable in the more non-linear and mixed semi-diurnal zone of the Camer- oon estuary. Indeed, the harmonic components in shallow water are not only astronomical. For example, the S2 component is strongly astronomic, but also radiational and includes non-linear combinations like S1 + S1, S3 − S1 and K1 + P1. M2 also includes a non-astronomical combinations of K1 + O1, N2 a combination of M1 + O1 and K1 a combination of S2 − P1. Therefore the resulting prediction can be inaccurate when it is performed over interval for which there is no available data.
The scope of this study is also limited due to the fact that tide gauges are sparse in Cameroon coastal areas. It is therefore of primary importance to build a more dense network of sea level gauges. This project would have to be designed and implemented with consideration for at-risk areas to complement the existing system.
In conclusion, the harmonic analysis method has been used to extract the tide constituents for five stations along the Cameroon coast. After corrections, particularly on the SM2 dataset, the prediction of tide derived from the analysis gave very accurate results compared to the data. However, the SMD station was only equipped with an analogue recorder and therefore the results for this station are less satisfactory due to the short duration of the recorded data and the important number of missing data. The use of hourly data instead of data sampled at 1 mn was found to generate negligible errors in harmonic analysis, even in estuaries where high frequency waves have a larger amplitude.
The maximum tide height in the Cameroon coast is observed in Cameroon estuary. In Limbe (SM SONARA) the tide amplitude is smaller but bigger than the one observed in the south coast (SM Kribi). The amplitudes of the fourth-diurnal waves in the estuary stations (SM4 and SMD) are higher than the ones of the stations located in the continental slope, which can be explained by non-linear interactions between M2 and S2 tides occurring in shallow waters. The strong fluctuations of rivers run-off also affects the long-term components of the tide, which can be observed at the SMD station located upstream in the Dibamba river.
Acknowledgements
Sea level data for this analysis were supplied by the Douala harbour, CERECOMA of Kribi, GLOSS tide gauge (Port SONARA). We would like to express our gratitude to IRD-DPF (Institut de Recherche pour le Développement-DPF) for its financial support. The authors also thank Dr. J. Folack for his collaboration, the IUT students for the digitalization of float type recorders data and Dr L. de Montera for his careful proofreading of the paper.
References
- Fonteh, M., Esteves, L.S. and Gehrels, W.R. (2009) Mapping and Valuation of Ecosystems and Economic Activities along the Coast of Cameroon: Implications of Future Sea Level Rise. EUCC―Die Küsten Union Deutschland e.V.: International Approaches of Coastal Research in Theory and Practice. Coastline Reports, 13, 47-63.
- Asangwe, C.K. (2006) The Douala Coastal Lagoon Complex, Cameroon: Environmental Issues, Administering Marine Spaces: International Issues. FIG publication No. 36.
- Jean, F., Mbome, L., Bokwe, A. and Tangang, A. (1999) Profil côtier du Cameroun, Projet Grand Ecosystème Marin du Golfe de Guinée. Ministère de l’Environnement et des Forêts. Yaoundé, Cameroun, 106 p.
- Olivry, J.C. (1974) Hydrologie du bief maritime de la Dibamba en periode d’étiage, note sur les étiages du mungo 9, ed. Mesres-Orstom, Paris.
- Olivry, J.C. (1986) Fleuves et Rivières du Cameroun. Collection Monographie Hydrologique 9, ed. Mesres-Orstom, Paris.
- Onguene, R., Duhaut, T., Lyard, F., Marsaleix, P., Allain, D, Pemha, E., Njeugna, E., Nguyen, C. and Du-Penhoat, Y. (2013) Hydrodynamic and Salinity Modeling of Estuaries in Central Africa. Application to the Cameroon Estuaries. 3rd JEAI-ALOC_GG International Workshop, Cotonou, 3-8 2013.
- Schureman, P. (1940) Manual of Harmonic Analysis and Prediction of Tides. United States Government Printing Office, 317 p. (reprinted with correction, 1976) United States Coast and Geodetic Survey Special Publication No. 98, Department Of Commerce, Washington DC.
- Pugh, D. (1987) Tides, Surges and Mean Sea-Level. John Wiley, London.
- Simon B. (2007) La marée océanique côtière. In: Institut Océanographique, Ed., Collection “Synthèses”, Paris, 433 p.
- Defant, A. (1961) Physical oceanography. Pergamon Press, New York.
- Manasrah (2013) Tide Variation and Signals during 2000-2004 in the Northern Gulf of Aqaba, Red Sea. Natural Science, 5, 1264-1271. http://dx.doi.org/10.4236/ns.2013.512154
- Wood, F. (2001) Tidal Dynamics: Theory and Analysis of Tidal Forces. Journal of Coastal Research, 1, Coastal Education Research Foundation, West Palm Beach, Fla.
- Araujo, I.B. and Pugh, D.T. (2008) Sea Levels at Newlyn, 1915-2005: Analysis of Trends for Future Flooding Risks. Journal of Coastal Research, 24, 203-212. http://dx.doi.org/10.2112/06-0785.1
- Boon, J.D. (2004) Secrets of the Tide: Tide and Tidal Current Analysis and Applications, Storm Surges and Sea Level Trends. Ellis Horwood, Chichester.
- Shaw, A.G.P. and Tsimplis, M.N. (2010) The 18.6 yr Nodal Modulation in the Tides of Southern European Coasts. Continental Shelf Research, 30, 138-151. http://dx.doi.org/10.1016/j.csr.2009.10.006
- US Army Corps of Engineers (1989) Water Levels and Wave Heights for Coastal Engineering Design. US Army Corps of Engineers, Hyattsville.
- Demerliac, M.A. (1974) Calcul du niveau moyen journalier. Annales Hydrographiques du SHOM 5 éme série, 49-57.
- Pugh, D. (2004) Changing Sea Levels, Effects of Tides, Weather and Climate. Cambridge University Press, Cambridge, 280 p.
- Wood, F. (2001) Tidal Dynamics: Extreme Tidal Peaks and Coastal Flooding. Journal of Coastal Research, 2, Coastal Education Research Foundation, West Palm Beach, Fla.
- Doodson, A.T. (1921) Harmonic Development of the Tide-Generating Potential. Proceedings of the Royal Society of London A, 100, 305-329. http://dx.doi.org/10.1098/rspa.1921.0088
NOTES
*Corresponding author.












