Open Journal of Statistics
Vol.09 No.01(2019), Article ID:90276,15 pages
10.4236/ojs.2019.91008
Internal Transactions for Multiple Risky Assets
Qiong Zhang1, Shuang Chen2
1School of Science, Hebei University of Technology, Tianjin, China
2School of Science, Beijing Institute of Petrochemical Technology, Beijing, China

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 2, 2019; Accepted: January 27, 2019; Published: January 30, 2019
ABSTRACT
Most of the articles about insider trading assume that there is only one risky asset in the market. On the basis of these papers, this thesis is mainly divided into three parts to study the situation of multiple risky assets in the market. In the first part, the situation of multiple risky assets in the market when two transactions are in progress is studied and then, the equilibrium when the market requires the internal traders to disclose the trading volume after each transaction is analyzed. In the second part, the equilibrium of multi-period based on the two phases of transaction is derived. The third part is the summary of the paper.
Keywords:
Insider Trading, Multiple, Risky Assets, Multi-Period, Noise Trader

1. Introduction
In modern finance mathematics, many models assume that all investors in the market have the same information and the same expectation. However, in real financial market or spot market, information asymmetry is common, such as the securities market. Traders with private information may release their own information at the beginning of the transaction, or they may conceal private information by adjusting their strategies. In 1985, Kyle [1] published a paper that analyzed the situation when there was only one risk-neutral internal trader. The results showed that the informed trader revealed his information at a constant rate when trading in continuous time. Based on this article, Holden and Subrahmanyam [2] [3] gave a model in which there are more than two informed traders and analyzed the impact of the number of insider traders to the market, with the result that their information was revealed almost immediately and the market depth is infinite. In addition, many experts have done further work on the basis of these papers, such as Hudart, Hughes, Levine [4] and Shunlong Luo [5] , Qiang Zhang [6] .
All the above papers assume that there is only one risky asset in the market. On the basis of these papers, this thesis mainly divides into two parts to study the situation of multiple risky assets in the market. In the first part, we study the situation of multiple risky assets in the market when two transactions are in progress. Furthermore, we analyze the equilibrium when the market requires the internal traders to disclose the trading volume after each transaction. In the second part, we derive the equilibrium of multi-period based on the two phases of transaction.
2. Two-Phase Transactions
2.1. Transactions Not Required for Publication of Trading Volume
Holden and Subrahmanyam model gives the two-phase equilibrium result when there is only one risky asset in the market and the internal trader is not required to reveal his trading volume. In this part, we consider the second-phase equilibrium results when there are multiple risky assets in the market without requiring internal traders to disclose their trading volume.
Next, we analyze one of these assets and call it asset j. The trading strategy of the i-th insider is shown as follows:
, where (1.1.1)
The pricing rules of market makers are as follows:
, where (1.1.2)
Then we can get the following formulas,
; (1.1.3)
, (1.1.4)
(1.1.5)
Obviously, the profit of the j-th asset is .
(1.1.6)
Nash equilibrium
Nash equilibrium refers to the situation in the game, for each participant, as long as others do not change their strategy, he cannot improve his situation. Nash proved that Nash equilibrium must exist on the premise that each participant has only a limited choice of strategies and allows mixed strategies. Take the price war between the two companies as an example, if the other side does not change the price, it can neither raise the price, or further lose the market; nor reduce the price, because there will be a loss sale. So the two companies can change the original interest pattern and seek a new benefit assessment and allocation scheme through negotiation, namely Nash equilibrium.
Sub-game perfect Nash equilibrium
becomes Nash equilibrium [7] , if all , , and other strategies have
;
;
;
and
2.2. Transaction Required to Announce Trading Volume
Lemma: Let , be two normal random vectors, where , , Given , the conditional distribution of (which we call ) is still normal. Accurately,
,
We assume that the trading volume of internal traders is disclosed (but not verified afterwards) before the second trading begins after the end of the first trading, then the above price and trading strategy are not balanced under the new framework [8] . Assuming that the market maker guesses that each internal trader’s strategy for j-th asset in the first period is , , the market
maker can speculate that when observing , thus his pricing rule is and . Insider traders will choose
strategy because they are aware of the behavior of market makers. Any such violation may lead to mispricing in the second period. Because the market maker chooses , the market depth is infinite and the second profit of the internal trader is infinite.
Obviously, any reversible strategy can not be an equilibrium strategy. We assume that the first stage strategy of an internal trader consists of two parts, one is the part that can be predicted with the information available to him, the other is the noise part , that is, the part that cannot be predicted by the information he has. is a normal distribution with 0 as its mean and as its variance, and it is independent of and . is the expected value [9] of under and , so . In the second phase of pricing, took the place of . . It is easy to know from symmetry that given a market maker’s linear pricing strategy, the only possible equilibrium is that these internal traders adopt the same strategy (because their information is identical), so we can analyze any one of them. Here we use backward induction to analyze internal trader 1.
2.2.1. The Optimization Problem of the Second Phase
In the case of given and , the second period optimal problem of internal trader 1 is shown below.
;
(1.2.1)
where .
Next is the maximization of the solution. We record the largest on the top of the equation as . First order derivation can be obtained from the upper form.
Let , we can obtain that (1.2.2)
;
(1.2.3)
The two order derivation is , so the two order condition is .
2.2.2. The Optimization Problem of the First Phase
Next, we study the optimization problem of the first phase.
;
(1.2.4)
Let , than we get the following formula from the first order condition.
Let , than we can obtain that
(1.2.5)
From the second-order condition we can obtain that
(1.2.6)
If our hypothetical mixed trading strategy holds in equilibrium, i.e.
(1.2.7)
(1.2.8)
then from the Formula (1.2.5) we can obtain that , and satisfy , ,
(1.2.9)
(1.2.10)
Combined with (1.2.9) and (1.2.10), we can get
(1.2.11)
(1.2.12)
From the conditions of market effectiveness, we can get
;
;
.
where
;
;
.
In conjunction with lemma , we can obtain that
1) (1.2.13)
Proof: , and are independent of each other.
a)
b)
2) (1.2.14)
Proof:
The next step is to find the expression of .
;
3) (1.2.15)
Proof:
(1.2.16)
From the three formulas of (1.2.12), (1.2.13), (1.2.14), we can get the following two formulas.
, (1.2.17)
Proof:
From the three formulas of (1.2.11), (1.2.16), (1.2.17), we can get the following formula.
(1.2.18)
According to Formula , we can obtain .
(1.2.19)
Combined with the eighth formula, we get .
(1.2.20)
The eleventh formula can be reduced to
(1.2.21)
(1.2.22)
In conclusion, we can get the following propositions.
Proposition: When the market requires the internal trader to announce the trading volume, the sub-game equilibrium has uniqueness. In this equilibrium, there are constants , , , , and , satisfying [10]
(1.2.23)
(1.2.24)
(1.2.25)
(1.2.26)
(1.2.27)
(1.2.28)
For all internal traders. constants , , , , and , satisfying
(1.2.29)
(1.2.30)
(1.2.31)
(1.2.32)
(1.2.33)
(1.2.34)
(1.2.35)
Analysis
The results show that , which means that the trading intensity of each internal trader in the first phase is not as strong as that of the second phase, because the trader does not consider the impact of the transaction on earnings in the second phase. At the same time, it can be seen from that the trader conceals his trading strategy through the noise trader’s trading.
3. Multi Period Transactions
We generalize the two-period results to the multi-period case, assuming that there is a total N-period transaction, the traders announce his trading volume after the end of each transaction. Transaction prices reflect the volume of transactions in the past and present.
First, the following proposition is given based on the two phase result.
Proposition In the market where M insiders exist, there is a unique subgame Nash equilibrium. In this equilibrium, there are constants , , , and to satisfy the following equations.
(2.1)
(2.2)
(2.3)
(2.4)
(2.5)
,
Given
and
, constants
,
,
, 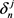 and
and 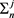 are the unique solutions of the following equations.
are the unique solutions of the following equations.
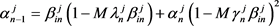 (2.6)
(2.6)
 (2.7)
(2.7)
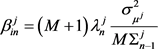 (2.8)
(2.8)
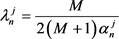 (2.9)
(2.9)
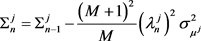 (2.10)
(2.10)
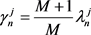 (2.11)
(2.11)
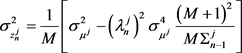 (2.12)
(2.12)
 ;
;
when n = N,
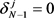 (2.13)
(2.13)
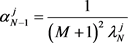 (2.14)
(2.14)
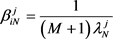 (2.15)
(2.15)
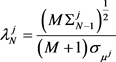 (2.16)
(2.16)
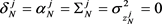 (2.17)
(2.17)
Proof: By using backward induction, the optimal problem of the period N of a trader i for given 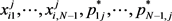 can be recorded as follows:
can be recorded as follows:
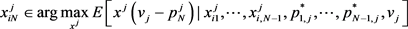


The first order derivative can be obtained for the upper form.

Let


Therefore







The first derivative of the upper form is

Let

Because of

Because 



It can be drawn from the above two formulas that
Thus


By market availability, we can get the following formula.

According to the results of the second phase, we can get the values of 



Combined with

Thus




The relation between 


Analysis
From the results of the proposition, we can see that the transaction volume is proportional to the value of the asset, but inversely proportional to the price of the asset in the previous period; the price of the asset is proportional to the total transaction volume of the asset; and the depth of the market is inversely proportional to the number of traders.
4. Conclusion
This paper mainly studies the trader’s trading strategy, market maker’s pricing rules and equilibrium conditions when the trader is not required to announce the volume of transactions and the trader is required to announce the volume of transactions in two periods. Then, according to the trading situation of two periods, we deduce the trading strategy of traders and the pricing rules of market makers in multi-period trading. The noise trader is also considered in this paper. From the two propositions in the paper, we can see the relationship between the variables.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Zhang, Q. and Chen, S. (2019) Internal Transactions for Multiple Risky Assets. Open Journal of Statistics, 9, 85-99. https://doi.org/10.4236/ojs.2019.91008
References
- 1. Kyle, A.S. (1985) Continuous Auctions and Insider Trading. Econometrica, 53, 1315-1335. https://doi.org/10.2307/1913210
- 2. Holden, C.W. and Subrahmanyam, A. (1992) Long-Lived Private Information and Imperfect Competition. Journal of Finance, 47, 247-270. https://doi.org/10.1111/j.1540-6261.1992.tb03985.x
- 3. Holden, C.W. and Subrahmanyam, A. (1994) Risk Aversion, Imperfect Competition and Long-Lived Information. Economics Letters, 44, 181-190. https://doi.org/10.1016/0165-1765(93)00288-Y
- 4. Huddart, S., Hughes, J.S. and Levine, C.B. (2001) Public Disclosure and Dissimulation of Insider Traders. Econometrica, 69, 665-681. https://doi.org/10.1111/1468-0262.00209
- 5. Luo, S.L. (2001) The Impact of Public Information on Insider Trading. Economics Letters, 70, 59-68. https://doi.org/10.1016/S0165-1765(00)00347-5
- 6. Luo, S.L. and Zhang, Q. (2002) Dynamic Insider Trading. AMS/IP Studies in Advanced Mathematics, 4, 93-104.
- 7. Liu, H. (2008) Internal Transactions in the Case of Information Asymmetry. Doctoral Thesis of Chinese Academy of Sciences, Beijing.
- 8. Liao, X.Q. and Zou, H.F. (2004) An Analysis of the Transaction Behavior of Internal Traders. World Economy, 11, 16-22.
- 9. Xiao, K. and Zhou, Y.H. (2014) Internal Trading in Incomplete Signals. Journal of Chongqing Technology and Business University (Natural Science Edition), 2, 50-55.
- 10. Xiao, K. and Zhou, Y.H. (2013) Internal Trading under Incomplete Noise Trading Information. Journal of Guizhou Normal University (Natural Sciences), 5, 56-60.
Notations
M: The number of internal traders
N: Total number of transactions























