Open Journal of Statistics
Vol.06 No.05(2016), Article ID:71275,10 pages
10.4236/ojs.2016.65067
Comparison of REML and MINQUE for Estimated Variance Components and Predicted Random Effects
Nan Nan1, Johnie N. Jenkins2, Jack C. McCarty2, Jixiang Wu3*
1Department of Mathematics and Statistics; South Dakota State University, Brookings, SD, USA
2Crop Science Research Laboratory USDA-ARS, Mississippi State, MS, USA
3Agronomy, Horticulture, and Plant Science Department, South Dakota State University, Brookings, SD, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 20, 2016; Accepted: October 15, 2016; Published: October 18, 2016
ABSTRACT
Linear mixed model (LMM) approaches have been widely applied in many areas of research data analysis because they offer great flexibility for different data structures and linear model systems. In this study, emphasis is placed on comparing the properties of two LMM approaches: restricted maximum likelihood (REML) and minimum norm quadratic unbiased estimation (MINQUE) with and without resampling techniques being included. Bias, testing power, Type I error, and computing time were compared between REML and MINQUE approaches with and without Jackknife technique based on 500 simulated data sets. Results showed that MINQUE and REML methods performed equally regarding bias, Type I error, and power. Jackknife- based MINQUE and REML greatly improved power compared to non-Jackknife based linear mixed model approaches. Results also showed that MINQUE is more time- saving compared to REML, especially with the use of resampling techniques and large data set analysis. Results from the actual cotton data analysis were in agreement with our simulated results. Therefore, Jackknife-based MINQUE approaches could be recommended to achieve desirable power with reduced time for a large data analysis and model simulations.
Keywords:
Linear Mixed Model Approaches, MINQUE, REML, Jackknife

1. Introduction
Linear mixed models (LMM) are a generalization of various linear models covering simple linear regression models, ANOVA models, and complex genetic models. LMM approaches including maximum likelihood (ML) [1] , restricted maximum likelihood (REML) [2] , and minimum norm quadratic unbiased estimation (MINQUE) [3] are among the most commonly used ones for variance component estimation and random effect prediction. Numerical comparisons of the statistical properties among these LMM approaches could help users choose appropriate approaches for various data analyses.
ML and REML approaches have been integrated into SAS [4] and into R such as lme4 [5] [6] and ASReml [7] . Due to their popularity and long-term availability, a wide range of applications in various areas, has occurred. For example, based on a recent google scholar search in May, 2016, more than 43,000 publications were available. Both ML and REML approaches are based on the assumption that data are normally distributed (Laird and Ware, 1982) and require iterations [8] . Compared to ML and REML, MINQUE approaches were less popular. However, MINQUE approaches do not require normally distributed data nor iterations [3] [9] . Thus, they could offer more flexibility with reduced computational intensity. Since 1989, MINQUE approaches have been widely used in quantitative genetics studies [10] - [19] .
Though LMM approaches are currently widely used, a potential issue associated with LMM is low power in statistical tests for variance components and random effects. With the use of jackknife methods, statistical powers could be significantly improved [20] - [22] . On the other hand, with resampling techniques, it is possible to generalize statistical tests for various parameters of interest. Resampling techniques including jackknife and permutation methods have been integrated in linear mixed model approaches and two R packages, minque and qgtools, which are currently available online [23] [24] .
The aim of this study was to compare statistical properties between REML and MINQUE approaches with and without a jackknife technique [25] through Monte Carlo simulations. A cotton data set [25] including 24 genotypes under two environments was used for both simulations and actual data analyses. These methods were compared regarding statistical power, Type I error, and computational time. Results including variance components and genotypic effects from actual data analysis were also compared. Results could provide statistical information on appropriate use of these LMM approaches.
2. Materials and Methods
2.1. Materials
Various data structures and related linear mixed models can be used for our simulations and actual data analysis. Without losing our focus of this study, we employed a cotton data set including 24 cotton genotypes under two locations each following a randomized complete block design with six replications [25] . The data were collected on the two sites at the research farm at Mississippi State University, Starkville, MS. The data structure was used for simulation study using the model detailed below (Equation (1)). Two agronomic traits: lint yield (LY), and lint percentage (LP), were included and used for our actual data analysis. The data set, cot, is currently available in the R package, minque [23] .
2.2. Statistical Model and Methods
Given the data structure, the observation 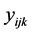 standing for the genotype j under the kth block in the environment i can be expressed by using the following linear mixed model:
standing for the genotype j under the kth block in the environment i can be expressed by using the following linear mixed model:
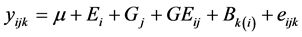 (1)
(1)
where 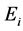 is an environmental effect and treated as fixed effect;
is an environmental effect and treated as fixed effect; 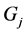 is a genotypic effect and treated as random;
is a genotypic effect and treated as random; 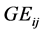 is a genotype-by-environment interaction effect and random;
is a genotype-by-environment interaction effect and random;  is a random block effect within environment; and
is a random block effect within environment; and 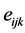 is the random error.
is the random error.
Two linear mixed model approaches, MINQUE and REML [2] [3] [9] , were applied. In addition, a randomized 10-fold Jackknife technique [21] was integrated with these two linear mixed model approaches. Therefore, four combinations of methods in total were used for both simulation and actual data analysis. To simplify our description, we defined these four combinations of methods as: M1 = MINQUE without jackknife; M2 = REML without jackknife; M3 = MINQUE with jackknife; and M4 = REML with jackknife. Regarding simulation studies, there could be numerous parameter settings, however, we only considered two representative parameter settings because the major aim of this study was to compare statistical properties among these four methods. The first setting was to preset all variance components to 20 (interested users may use other settings), targeting power and bias. The second setting was to preset all variance components to zero except the random error variance which was 20, targeting Type I error and bias for all variance components except random error variance. For each parameter setting, five hundred simulated data sets [26] [27] were generated and analyzed by each combination of these four methods. Statistical properties including bias, and testing power/Type I error were calculated for each method [28] [29] . Type I error is the false significance rate for a preset variance component being zero while testing power is the true significance rate for a positive preset variance component over 500 simulations. The bias is for each variance component is the deviation of mean estimated variance component from the preset variance component (0 or 20 in this study) which is given by Equation (2):
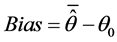 (2)
(2)
where, 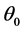 is a preset variance component and
is a preset variance component and  is mean estimated variance component. We briefly defined the following terms. The standard error (SE) is defined by
is mean estimated variance component. We briefly defined the following terms. The standard error (SE) is defined by , a standard error for a mean estimated variance component. In addition, computational time (in seconds) was recorded for every 100 simulations out of 500 simulations (Table 3).
, a standard error for a mean estimated variance component. In addition, computational time (in seconds) was recorded for every 100 simulations out of 500 simulations (Table 3).
For actual data analysis, variance components were estimated by REML and MINQUE approaches and genotypic effects were predicted by the adjusted unbiased prediction method [30] . All simulations and data analyses were conducted using the functions that are available in the R package minque [23] under the R Studio environment [31] . The computational time recorded for simulation was based on HP Z440 with 32G ram under Windows 7 64-bit operation system.
3. Results and Discussion
3.1. Simulation Results
Bias, standard error, power, Type I error, and computational time based on 500 simulated data for four methods are summarized in Table 1 and Table 2. Results showed that bias for each variance component was similar among the four methods (M1-M4) (Table 1 and Table 2). Standard errors (SE) for each variance component among 500 estimates were also similar for the four methods (Table 1 and Table 2). Non-Jackknife based MINQUE and REML methods (M1 and M2) had similar power (at the probability level of 5%). However, Jackknife based REML and MINQUE methods (M3 and M4) had improved power for variances of genotypic and block effects compared to non-Jackknife based methods(M1 and M2) (Table 1). All four methods yield acceptable Type I error (around 5% or lower) for all variance components except the random error variance component (Table 2). Overall, both MINQUE and REML performed equally well regarding bias, power, and Type I error for variance component estimation. However, jackknife based MINQUE and REML could greatly improve power with acceptable Type I error compared to non-jackknife based methods.
Computational time in seconds used for each 100 simulations for each method and parameter setting is given in Table 3. Though other tasks were possible active during
Table 1. Estimated bias, standard error (SE), and power (at 0.05) for four preset components based on 500 simulated data sets with four methods.
Ɨ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife ǂ:  = variance component for genotype effects;
= variance component for genotype effects; 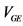 = variance component for genotype and environment interaction effects;
= variance component for genotype and environment interaction effects;  = variance component for block effects; and
= variance component for block effects; and 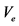 = variance component for random error.
= variance component for random error.
Table 2. Estimated bias, standard error (SE), and Type I error (at 0.05) for four preset components based on 500 simulated data sets with four methods.
Ɨ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife ǂ:  =variance component for genotype effects;
=variance component for genotype effects; 


Table 3. Computational time (seconds) recorded each 100 simulations out of 500 simulations for each method and parameter setting.
Ɨ: Parameter settings 1: all variance components were preset as 20; Parameter settings 2: all variance components were preset as 0 except the error variance component being set to 20. ǂ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife.
the simulation process, computational time among five 100-simulations was similar given a particular parameter setting and method. Among four methods, M1, M2, and M3 were time-saving (less than two minutes) while M4 took much longer (over 10 minutes) than the other three methods. For parameter setting 1, M2 (REML without jackknife) took 14.6 seconds longer than M1 (MINQUE without jackknife) and M3 (MINQUE with jackknife) was only 24.1 seconds longer than M1 over 500 simulations (Table 3). For parameter setting 2, M2 (REML without jackknife) was little longer than M1 and M3, which had similar computing time. M1 and M3 appeared more time-saving for the parameter setting 2 compared to the parameter setting 1. Our repeated simulations showed the same pattern (results not shown). One possible reason is that REML may need more iterations to converge for zero or negative variance components than for positive variance components. M4 was over eight-fold slower compared to M3 for the parameter setting 1 while 17 times slower for the parameter setting 2. Therefore, the results showed that MINQUE approach with or with jackknife was very time-saving yet yielded almost identical results compared to REML approach especially integrated with resampling process.
3.2. Actual Data Analysis
With the same model, two agronomic traits: cotton lint yield (LY) and lint percentage (LP), were analyzed by the same four methods used in our simulation studies. Estimated variance components for these two traits are summarized in Table 4 and Table 5 while predicted genotypic effects are presented in Table 6 and Table 7. Results showed that estimated variance components were similar for four methods for each of two traits while M3 and M4 yielded smaller standard error compared to M1 and M2 (Table 4 and Table 5). On the other hand, all four methods yielded similar predicted genotypic effects while M3 and M4 had lower standard errors compared to M1 and M2 (Table 6 and Table 7). The results in Tables 4-7 showed that Jackknife technique integrated
Table 4. Estimated variance components for lint yield (LY) by four methods.
Ɨ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife ǂ: 



Table 5. Estimated variance components for lint percentage (LP) by four methods.
Ɨ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife ǂ: 



Table 6. Predicted genotypic effects for lint yield (LY, kg/ha) by four methods.
Ɨ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife.
with two LMM approaches could significantly reduce standard errors for these estimated variance components and predicted effects and thus statistical power for these parameters increased considerably with the use of jackknife method, as shown in Table 1. The results from actual data analysis were highly consistent with the simulated results.
Based on the results from our simulation and actual data analysis in this study, several clear conclusions could be drawn: 1) MINQUE and REML approaches perform equally well (M1 vs M2 and M3 vs M4) regarding variance component estimation and random effect prediction); 2) Jackknife based MINQUE and REML approaches could
Table 7. Predicted genotypic effects for lint percentage (LP, %) by four methods.
Ɨ: M1 = MINQUE approach without Jackknife; M2 = REML approach without Jackknife; M3 = MINQUE approach with Jackknife; and M4 = REML approach with Jackknife.
improve test power while maintaining acceptable Type I error (M1 vs M3 and M2 vs M4); and 3) MINQUE approaches provide less computational intensity especially integrated with jackknife approaches or for simulation study compared to REML approaches.
Though, in this study, we only reported results based on a given data set, many other results also showed the similar patterns that we have found in this study. The methods used for simulations and actual data analysis and example R scripts are available in the two R packages, minque and qgtools [23] [24] . Interested readers may follow these R scripts to conduct their own statistical data analysis and model comparisons and evaluations.
Cite this paper
Nan, N., Jenkins, J.N., McCarty, J.C. and Wu, J.X. (2016) Comparison of REML and MINQUE for Estimated Variance Components and Predicted Random Effects. Open Journal of Statistics, 6, 814-823. http://dx.doi.org/10.4236/ojs.2016.65067
References
- 1. Hartley, H.O. and Rao, J.N.K. (1967) Maximum-Likelihood Estimation for the Mixed Analysis of Variance Model. Biometrika, 54, 93-108.
http://dx.doi.org/10.1093/biomet/54.1-2.93 - 2. Patterson, H.D. and Thompson, R. (1971) Recovery of Inter-Block Information When Block Size Are Unequal. Biometrika, 58, 545-554.
http://dx.doi.org/10.1093/biomet/58.3.545 - 3. Rao, C.R. (1971) Estimation of Variance and Covariance Components—MINQUE Theory. Journal of Multivariate Analysis, 1, 257-275.
http://dx.doi.org/10.1016/0047-259X(71)90001-7 - 4. Littell, R.C., et al. (2006) SAS for Mixed Models. SAS Institute Inc., Cary, NC.
- 5. Bates, D., Machler, M., Bolker, B. and Walker, S. (2015) Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67, 1-48.
http://dx.doi.org/10.18637/jss.v067.i01 - 6. Demidenko, E. (2013) Mixed Models: Theory and Applications with R. John Wiley & Sons Inc., Hoboken.
- 7. Butler, D., Cullis, B. and Gilmour, A. (2007) ASReml-R: An R Package for Mixed Models Using Residual Maximum Likelihood.
https://www.r-project.org/conferences/useR-2007/program/presentations/butler.pdf - 8. Searle, S.R., Casella, G. and McCulloch, C.E. (1992) Variance Components. Wiley, New York.
http://dx.doi.org/10.1002/9780470316856 - 9. Zhu, J. (1989) Estimation of Genetic Variance Components in the General Mixed Model. North Carolina State University, Raleigh, NC.
- 10. Zhu, J. (1995) Analysis of Conditional Genetic-Effects and Variance-Components in Developmental Genetics. Genetics, 141, 1633-1639.
- 11. McCarty, J.C., Jenkins, J.N., Tang, B. and Watson, C.E. (1996) Genetic Analysis of Primitive Cotton Germplasm Accessions. Crop Science, 36, 581-585.
http://dx.doi.org/10.2135/cropsci1996.0011183X003600030009x - 12. Tang, B., Jenkins, J.N., Watson, C.E., McCarty, J.C. and Creech, R.G. (1996) Evaluation of Genetic Variances, Heritabilities, and Correlations for Yield and Fiber Traits among Cotton F2 Hybrid Populations. Euphytica, 91, 315-322.
http://dx.doi.org/10.1007/BF00033093 - 13. Zhu, J. and Weir, B.S. (1996) Mixed Model Approaches for Diallel Analysis Based on a Bio-Model. Genetics Research, 68, 233-240.
http://dx.doi.org/10.1017/S0016672300034200 - 14. Lou, X.Y. and Zhu, J. (2002) Analysis of Genetic Effects of Major Genes and Polygenes on Quantitative Traits. II. Genetic Models for Seed Traits of Crops. Theoretical and Applied Genetics, 105, 964-971.
http://dx.doi.org/10.1007/s00122-002-0958-5 - 15. McCarty, J.C., Jenkins, J.N. and Wu, J.X. (2004) Primitive Accession Derived Germplasm by Cultivar Crosses as Sources for Cotton Improvement: I. Phenotypic Values and Variance Components. Crop Science, 44, 1226-1230.
http://dx.doi.org/10.2135/cropsci2004.1226 - 16. Lou, X.Y. and Yang, M.C.K. (2006) Estimating Effects of a Single Gene and Polygenes on Quantitative Traits from a Diallel Design. Genetica, 128, 471-484.
http://dx.doi.org/10.1007/s10709-006-7853-y - 17. Wu, J., Xu, H. and Zhu, J. (1997) An Approach to Eliminating Systematic Errors in Genetic Analysis. International Conference on Mathematical Biology, Hangzhou, 26-29 May 1997, 265-270.
- 18. Jenkins, J.N., et al. (2006) Genetic Effects of Thirteen Gossypium barbadense L. Chromosome Substitution Lines in Top Crosses with Upland Cotton Cultivars: I. Yield and Yield Components. Crop Science, 46, 1169-1178.
http://dx.doi.org/10.2135/cropsci2005.08-0269 - 19. Saha, S., Wu, J., Jenkins, J.N., McCarty, J.C. and Stelly, D.M. (2013) Interspecific Chromosomal Effects on Agronomic Traits in Gossypium hirsutum by AD Analysis Using Intermated G. barbadense Chromosome Substitution Lines. Theoretical and Applied Genetics, 126, 109-117.
http://dx.doi.org/10.1007/s00122-012-1965-9 - 20. Wu, J., Jenkins, J.N. and McCarty, J.C. (2008) Testing Variance Components by Two Jackknife Techniques. Proceedings of Applied Statistics in Agriculture, Manhattan, 27-29 April 2008, 1-17.
- 21. Wu, J.X., et al. (2013) Genetic Analysis without Replications: Model Evaluation and Application in Spring Wheat. Euphytica, 190, 447-458.
http://dx.doi.org/10.1007/s10681-012-0835-5 - 22. Zhu, J. (1998) Genetic Models and Analytical Methods. China Agricultural Press, Bejing.
- 23. Wu, J. (2014) Minque: An R Package Fir Linear Mixed Model Analyses.
https://cran.r-project.org/web/packages/minque/index.html - 24. Wu, J., Jenkins, J.N. and McCarty, J.C. (2014) qgtools: Tools for Quantitative Genetics Data Analyses.
https://cran.r-project.org/web/packages/qgtools/index.html - 25. Wu, J.X., Jenkins, J.N., McCarty, J.C. and Glover, K. (2012) Detecting Epistatic Effects Associated with Cotton Traits by a Modified MDR Approach. Euphytica, 187, 289-301.
http://dx.doi.org/10.1007/s10681-012-0770-5 - 26. Bondalapati, K.D., Wu, J. and Glover, K.D. (2014) An Augmented Additive-Dominance (AD) Model for Analysis of Multi-Parental Spring Wheat F2 Hybrids. Australian Journal of Crop Science, 8, 1441-1447.
- 27. Bondalapati, K.D., Wu, J.X., Jenkins, J.N. and McCarty, J.C. (2015) Field Experimental Design Comparisons to Detect Field Effects Associated with Agronomic Traits in Upland Cotton. Euphytica, 206, 747-757.
http://dx.doi.org/10.1007/s10681-015-1512-2 - 28. Wu, J., Saha, S., Jenkins, J.N., McCarty, J.C. and Stelly, D.M. (2006) An Additive-Dominance Model to Determine Chromosomal Effects in Chromosome Substitution Lines and Other Gemplasms. Theoretical and Applied Genetics, 112, 391-399.
http://dx.doi.org/10.1007/s00122-005-0042-z - 29. Wu, J., Jenkins, J.N., McCarty, J.C. and Wu, D. (2006) Variance Component Estimation Using the Additive, Dominance, and Additive × Additive Model When Genotypes Vary across Environments. Crop Science, 46, 174-179.
http://dx.doi.org/10.2135/cropsci2005.04-0025 - 30. Zhu, J. (1993) Methods of Predicting Genotype Value and Heterosis for Offspring of Hybrids. Journal of Biomathematics, 8, 32-44. (In Chinese)
- 31. RStudio (2015) RStudio: Integrated Development Environment for R. Boston, MA.


