Received 27 August 2015; accepted 20 October 2015; published 23 October 2015

ABSTRACT

This paper considers the computation of sparse solutions of the linear complementarity problems LCP(q, M). Mathematically, the underlying model is NP-hard in general. Thus an l_p(0 < p < 1) regularized minimization model is proposed for relaxation. We establish the equivalent unconstrained minimization reformation of the NCP-function. Based on the generalized Fiser-Burmeister function, a sequential smoothing spectral gradient method is proposed to solve the equivalent problem. Numerical results are given to show the efficiency of the proposed method.

Keywords:

Linear Complementarity Problem, Sparse Solution, Spectral Gradient, Generalized Fischer-Burmeister

1. Introduction

Given a matrix 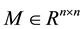and an n-dimensional vector q, the linear complementarity problem, denoted by LCP(q, M), is to find a vector 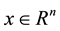such that

.

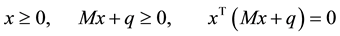The set of solutions to this problem is denoted by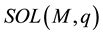. Throughout the paper, we always suppose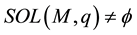. The LCP has many wide applications in physics, engineering, mechanics, and economics design [1] [2] . Numerical methods for solving LCPs, such as the Newton method, the interior point method and the non-smooth equation methods, have been extensively investigated in the literature. However, it seems that there are few methods to solve the sparse solutions for LCPs. In fact, it is very necessary to research the sparse solution of the LCPs such as portfolio selection [3] [4] and bimatrix games [5] in real applications.

In this paper, we consider the sparse solutions of the LCP. We call 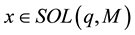a sparse solution of LCP (q, M) if 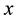is a solution of the following optimization problem

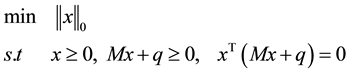(1)

To be more precise, we seek a vector by solving the l₀ norm minimization problem, where 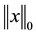stands for the number of nonzero components of x. A solution of (1) is called the sparsest solution of the LCP.

Recently, Meijuan Shang, Chao Zhang and Naihua Xiu design a sequential smoothing gradient method to solve the sparse solution of LCP [6] . We inspire by the model and use the spectral method based on the generalized Fischer-Burmeister function to solve our new model (3). The spectral method is proposed by Barzilai and Borwein [7] and further analyzed by Raydan [8] [9] . The advantage of this method is that it requires little computational work and greatly speeds up the convergence of gradient methods. Therefore, this technique has received successful applications in unconstrained and constrained optimizations [10] -[13] .

In fact, the above minimization problem (1) is a sparse optimization with equilibrium constraints. From the problem of constraint conditions, as well as the non-smooth objective function, it is difficult to get solutions due to the equilibrium constraints to overcome the difficultly, and we use the NCP-functions to construct the penalty of violating the equilibrium constraints.

A function φ: R² → R¹ is called a NCP-function, if for any pair.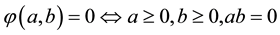

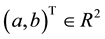A popular NCP-functions is the Fischer-Burmeister (FB), which is defined as

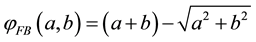
The Fischer-Burmeister function has many interesting properties. However, it has limitations in dealing with monotone complementarity problems since it is too flat in the positive orthant, the region of main interest for a complementarity problem. In terms of the above disadvantage of the Fischer-Burmeister function, we consider the following generalized Fischer-Burmeister function [10] .

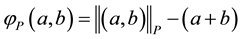(2)

where p is any fixed real number from 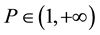and 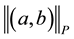denotes the p-norm, i.e.

In other words, in the function, we replace the 2-norm of in the FB function by a more general p-norm of. The function is still an NCP-function.

Define by

where with and. Obviously, if and only if. By further employing the l_p regularization term for seeking sparsity, we obtain the following unconstrained minimization problem to approximate

(3)

where is a given regularization parameter, and for any 0 < p < 1. We call (3) as l_p

regularized minimization problem.

Let us denote the first term of (3) by the function. That is

(4)

For any given, the function is shown to possess all favorable properties of the FB function; we can see [8] . It plays an important part in our study throughout the paper. We observe in [14] [15] that P has a great influence on the numerical performance of certain descent-type methods; a larger P yields a better convergence rate, whereas a small P often gives a better global convergence.

The paper is organized as follows: In Section 2, we present absolute lower bounds for nonzero entries in local solution of (3). In section 3, we approximate the minimal zero norm solutions of the LCP. In section 4, we give a sequential smoothing spectral gradient method to solve the model. In Section 5, numerical results are given to demonstrate the effectiveness of the sequential smoothing spectral gradient method.

2. The l_p Regularized Approximation

In this section, we consider the minimizers of (3). We study the relation between the original model (1) and the l_p regularized model (3), which indicates the regularized model is a good approximation. We use a threshold lower bound L [6] for nonzero entries in local minimizers and the choice of the l_p minimization problem (3).

2.1. Relation between (3) and (1)

The following result is given in [6] , which is essentially based on some results given by Chen Xiaojun [14] .

Lemma 2.1. [6] for any fixed the solution set of (3) is nonempty and bounded. Let be a solution

of (3), and be any positive sequence converging to 0. If, then has at least one accumulation point, and any accumulation point of is a solution of (3). That is, for any satisfied

and.

2.2. Lower Bounds for Nonzero Entries in Solutions

In this section, we extend the above result to the l_p norm regularization model (2) for approximating minimal l₀ norm solutions of the LCP. We provide a threshold lower bound L > 0 for any local minimizer, and show

that any nonzero entries of local minimizers must exceed L. Since, the objective function

is bound below and if. Moreover, the set of local minimizers of (3) is nonempty and bounded.

Lemma 2.2. [6] let be any local minimizer of (3) satisfying for an arbitrarily given point. Set

(5)

Then we have: for any.

Moreover, the number of nonzero entries in is bounded.

Let us denote the first term of (3) by the function. That is

(6)

First we present some properties of and.

Lemma 2.3. [12] let be given by (3). Then, the following properties hold:

1) is a positive homogeneous and sub-additive NCP-function.

2) is strongly semismooth.

3) If with, or, or, , then

when.

4) Given a point, very element in the generalized gradient has the representation, where

and for

sgn(.) represents the sign function; and are real numbers that satisfy.

Theorem 2.1. The function is continuously differentiable everywhere and the gradient of can be obtained by

(7)

where and are diagonal matrices whose diagonal element is giv-

en by

where is any vector satisfying.

3. Smoothing Method for l_p Regularization

Most optimization algorithms are efficient only for convex and smooth problems. However, some algorithms for

Non-smooth and non-convex optimization problems have been developed recently. Note that the term (0 <

p < 1) in (3) is neither convex nor Lipschitz continuous in. Solving the non-convex, non-Lipschitz continuous minimization problem is not easy. We use some approximation methods to surmount the non-Lipschitz continuity problem in solving (3).

Smoothing Counterpart for (3)

For, let

(8)

It is clear to see that, for any,

and is continuously differentiable with

We can construct a smoothing approximation of (2) as

(9)

by noting that is continuously differentiable, and since

(10)

for any.

Let denote the set of local minimizers of (10). We have the similar results as in Lemmma 2.1 and 2.2, corresponding to the smoothing counterpart (10).

Theorem 3.1. Let be a sequence of vectors being global minimizers of (10) with as.

Then, any accumulation point of is a global minimizer of (3).

Proof. Let be a global minimizer of (3) and be an accumulation point of.

We can deduce from (11) that

On the other hand, we have, and consequently

Which indicates is a global minimizer of (3).

Lemma 3.2. [6] for any, let be any local minimizer of (14) satisfying for an arbitrarily given initial points. Let L be defined in Lemma 2.2. Then, we have for any

4. SS-SG Algorithm

We suggest a sequential Smoothing Spectral Gradient (SS-SG) Method to solve (3). With the SS-SG method, we need the Spectral Gradient method as the main step for decreasing the objective value. The smoothing method is very easy to implement and efficient to deal with optimization; see [15] .

We first introduce the spectral projected gradient method in [8] as follow.

Algorithm 1. Smoothing Spectral Gradient Method

Step 0: Choose an initial point, and parameters, ,. Let, ,.

Step1: Let, , where,. If

, then stop.

Step 2: Compute the step size by the Armijo line search, where satisfies

Set.

Step 3: If, then set; otherwise, choose.

Algorithm 2. Sequential Smoothing Spectral Gradient Method

Step 1: Find by using the algorithm 1 to solve

Step 2: Compute

Use the lower bound to set the entries of with small values to zeros and obtain the computed solution with

Step 3: Decrease the parameter and set.

5. Numerical Experiments

In this section, we test some numerical experiments to demonstrate the effectiveness of our SG algorithm. In order to illustrating the effectiveness of the SS-SG algorithm we proposed, we introduce another algorithm of talking the LCPs. In [6] , the authors designed a sequential smoothing (SSG) method to solve the l_p regularized model and get a sparse solution of LCP(q, M). Numerical experiments show that our algorithm is more effective than (SSG) algorithm.

The program code was written in and run in MATLAB R2013 an environment. The parameters are chooses as, and. The maximum number of iterations in step 1 is set to be 2000. We end the SS-SG algorithm in Step 1, if and, or it reaches the maximum number of iterations.

5.1. Test for LCPs with Positive Semidefinite Matrices

Example 1. We consider the LCP(q, M) with

The solution set is.

When, the vector is the sparse solution of LCP(q, M). We choose P = 10, p = 0.1 in (3) for this small example, and use our SS-SG algorithm with the regularization parameter. We use the initial point, we get a minimal norm solution and the distance

.

Example 2. We consider the LCP(q, M) with

The solution set is

When, the vector is the sparse solution of LCP(q, M). When, the vector

is the sparse solution of LCP(q, M). We choose the same parameters as Example 1. We use the initial point, we get a minimal norm solution and the distance

. We use the initial point, we get a minimal norm solution and the distance.

These examples show that, given the proper initial point, our algorithm can effectively find an approximate sparse solution.

5.2. Test for LCPs with Z-Matrix [6]

Let us consider LCP(q, M) where

and

Here is the identity matrix of order n and. Such a matrix M is widely used in statistics. It is clear that Mis a positive semidefinite Z-matrix. For any scalar, we know that the vector is a solution to LCP(q, M), since it satisfies that

Among all the solutions, the vector is the unique sparsest solution. We test the SS-SG algorithm for different dimensions with n = 100, 300, 500, 1000, 1300, respectively. In this set of experiments, we set.The results are displayed in Table 1.

In Table 1, “” denotes the Euclidean distance between and the true sparsest, and “time” denotes the computational time in seconds. Form Table 1, we can see that the SS-SG algorithm is effective to find the sparse solution of LCPs.

In order to test the effectiveness of the SS-SG algorithm, we compare with the SSG algorithm of talking the LCPs. In [10] , the authors use the Fiser-Burmeister function established a l_p (0 < p < 1) regularized minimization model and designed a SSG method to solve the LCPs. The results are displayed in Table 2, where “_” denotes the method is invalid. Although the sparsity is same and the recovered errors are pretty small, the average cpu time less than the SSG algorithm.

6. Conclusion

In this paper, we have studied a l_p (0 < p < 1) model based on the generalized FB function defined as in (2) to find the sparsest solution of LCPs. Then, an l_p normregularized and unconstrained minimization model is proposed for relaxation, and we use a sequential smoothing spectral gradient method to solve the model. Numerical results demonstrate that the method can efficiently solve this regularized model and gets a sparsest solution of LCP with high quality.

Acknowledgements

This work is supported by Innovation Programming of Shanghai Municipal Education Commission (No. 14YZ094).

Cite this paper

ChangGao,ZhenshengYu,FeiranWang, (2015) Spectral Gradient Algorithm Based on the Generalized Fiser-Burmeister Function for Sparse Solutions of LCPS. Open Journal of Statistics,05,543-551. doi: 10.4236/ojs.2015.56057

References