Open Journal of Statistics
Vol.04 No.11(2014), Article ID:52860,5 pages
10.4236/ojs.2014.411090
On Rotational Robustness of Shapiro-Wilk Type Tests for Multivariate Normality
Richie Lee, Meng Qian, Yongzhao Shao
Division of Biostatistics, New York University School of Medicine, New York, USA
Email: shaoy01@nyu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 October 2014; revised 10 November 2014; accepted 16 November 2014
ABSTRACT
The Shapiro-Wilk test (SWT) for normality is well known for its competitive power against numerous one-dimensional alternatives. Several extensions of the SWT to multi-dimensions have also been proposed. This paper investigates the relative strength and rotational robustness of some SWT-based normality tests. In particular, the Royston’s H-test and the SWT-based test proposed by Villaseñor-Alva and González-Estrada have R packages available for testing multivariate normality; thus they are user friendly but lack of rotational robustness compared to the test proposed by Fattorini. Numerical power comparison is provided for illustration along with some practical guidelines on the choice of these SWT-type tests in practice.
Keywords:
Multivariate Normality, R Packages, Robust Power, Shapiro-Wilk Test, Rotational Robustness

1. Introduction
Normal distributions are of central importance in statistical inference and in numerous applications. Thus, testing for normality including assessing multivariate normality has been studied extensively in statistics. For instance, in a research monograph, Thode [1] reviewed more than 30 formal statistical procedures proposed specifically for testing normality. For univariate data, the Shapiro-Wilk test (SWT) [2] for normality is the well- known benchmark of omnibus tests in terms of competitive power performance against a broad range of alternatives. Many extensions of the univariate SWT to multi-dimensions have been developed [1] , and at least two R packages for testing multivariate normality have recently been made based on the SWT-based tests by Royston [3] - [7] and Villaseñor-Alva and González-Estrada [8] [9] . The recently developed R-packages make the two SWT-based tests quite user-friendly thus have potential to be widely used by many practitioners in various fields of applications. Therefore, assessing the relative strength and robustness of these normality tests and providing insights and guidelines on when to use them would be of practical interest. This paper discusses the relative strength and rotational robustness of these user-friendly SWT-based tests and provides some guidelines for selecting tests in practical applications. In the next section we briefly review the original SWT [2] and two SWT-based tests for multivariate normality with R packages [3] - [9] . Section 3 discusses rotational robustness and the FA test [10] . Section 4 discusses the Iris data example and reports Monte Carlo simulation results. Section 5 provides some guidelines and remarks. The R code for the FA test is provided in the appendix.
2. The SWT-Based Normality Tests with R-Packages
Originally created to test univariate distributions for normality, given univariate data 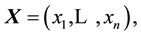 the Shapiro-Wilk test (SWT) [2] statistic is
the Shapiro-Wilk test (SWT) [2] statistic is

where  are the order statistics of the univariate data
are the order statistics of the univariate data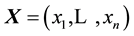 ,
,  is the sample mean, and the constants
is the sample mean, and the constants  are
are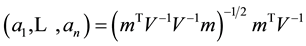 , with
, with 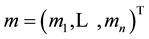 and
and  being the mean
being the mean
vector and covariance matrix of the order statistics of a random standard normal sample of size . The univariate SWT can be performed easily in R using the function shapiro.test based on Royston’s algorithms [3] [4] . The Shapiro-Wilk test (SWT) for normality is well known for its competitive power against numerous one-di- mensional alternatives. Many extensions of the SWT to the multivariate case have been proposed in the literature including Royston’s H-test [3] - [7] and a new multivariate extension of the SWT by Villaseñor-Alva and González-Estrada [8] . The first step in the extension of SWT proposed in [8] is to standardize the multiva-
. The univariate SWT can be performed easily in R using the function shapiro.test based on Royston’s algorithms [3] [4] . The Shapiro-Wilk test (SWT) for normality is well known for its competitive power against numerous one-di- mensional alternatives. Many extensions of the SWT to the multivariate case have been proposed in the literature including Royston’s H-test [3] - [7] and a new multivariate extension of the SWT by Villaseñor-Alva and González-Estrada [8] . The first step in the extension of SWT proposed in [8] is to standardize the multiva-
riate data  by substracting the sample mean
by substracting the sample mean 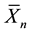 and multiplying by the square root of the
and multiplying by the square root of the
inverse of its covariance matrix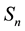 . It is known that the covariance matrix
. It is known that the covariance matrix 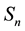 of a
of a 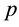 -variate normal is non-
-variate normal is non-
degenerate with probability one. Without loss of generality, let  be the symmetric square root of
be the symmetric square root of 



Under the null hypothesis, 

where 



age called mvShapiroTest that makes it very user friendly [9] . Moreover, power simulations against many alternatives reported in [8] indicate that the new test has competitive power compared to many well-known normality tests including the HZ test of Henze and Zirkler [11] . Similarly, the well-known Royston’s extension of SWT has also been made into an R-package recently called royston [7] . Both Villaseñor-Alva and González- Estrada [8] and Royston developed effective numerical approximations to the null distribution of the normality tests so that p-values can easily be estimated for any given sample size. Thus the R-packages make these tests much more user-friendly than other SWT-based tests for multivariate normality in the literature [1] [12] - [14] . In addition, the royston package can also draw q-q plots thus facilitating visualization of the non-normality in the data [7] . Given the importance of assessing multivariate normality in practical applications, it is of practical interest to systematically investigate the relative strength of these user-friendly normality tests and provide potential guidelines about test selection among these candidate tests in practice.
3. Rotational Robustness and the FA Test of Fattorini
The multivariate normal distributions have rotational invariance. In particular, 






[15] . When 








roTest or the Royston test. The FA test statistic is given by







bust power properties of the FA test, Thode [1] recommended the FA test as a generally powerful multivariate normality test besides the HZ test by Henze and Zirkler [11] after reviewing more than 30 tests for normality including both SWT-based and non-SWT based tests. The HZ test uses empirical characteristic functions instead of using extensions of the SWT.
4. The Iris Data Example and Numerical Studies
4.1. The Iris Data Example
The Iris data set is a well-known multivariate data set collected to measure the morphologic variation of Iris flowers of three related species. The data set consists of 50 samples from each of three species of Iris including setosa, virginica and versicolor. For each sample, four variables were measured including the length and the width of the sepals and petals, in centimeters. Fisher [16] used the Iris data to demonstrate the use of unclassified observations in estimating discriminant function. The non-normality of the multivariate Iris data has been investigated by many statisticians [17] [18] . For illustration, we consider the bivariate normality of the Iris data set by using the length and the width of the sepals of two of the species Iris setosa, and Iris versicolor that are the first two columns and first 100 rows of the Iris data. The p-values of the mvShapiro.Test and royston.test in R were 0.26 and 0.37, respectively. Thus both tests fail to detect non-normality when testing X. However, if we test U(X) instead of X for normality, both the mvShapiro.Test and royston.test have very small p-values, 0.0003 and 0.0018, respectively, providing significant evidence of non-normality. Thus in this case, the two tests based on testing U(X) are more powerful than testing X. For the above data the FA test has p-values < 0.001 in testing both X and U(X) indicating rotational robustness.
4.2. Simulation Studies
From the above Iris data example, it is clear that testing for X and testing for U(X) can have dramatically different powers for the mvShapiro.Test and royston.test, we conducted further simulations for a wide variety of alternatives. Indeed, neither of these two tests has robust power against rotational alternatives when the marginal distributions of X are independent. They are seriously lack of rotational robustness compared to the FA test. More specifically, the R package mvShapiroTest was used to evaluate the test statistics, the critical values, and powers of the test discussed in [8] [9] . The mvShapiro.Test function was applied to 500,000 independent samples from the standard bivariate normal distribution to evaluate the test statistics and the percentiles corresponding to alpha = 5% and 1%. The estimated power was the percentage of the simulated mvShapiro.Test$statistic
that exceeded the previously calculated critical values under 50,000 samples from each alternative. Similarly the royston package in R is used to calculate critical values of the royston.test based on 500,000 samples from the standard bivariate normal distribution and the empirical power based on 50,000 samples from each alternative distribution. Using the same set up, the critical values and power of the FA test [10] were obtained using the R code provided in the Appendix. Note that all three tests are applied to standardized data in our simulations to make sure Type I errors are correct under multivariate normality with unknown mean vector and covariance matrix and to ensure fair power comparison.
4.3. Simulation Findings
The simulated power is illustrated in Table 1 for the sample size n = 50 and
Table 1. Power (in percent): (α = 5%, n = 50).
ternative χ2(5)*χ2(5) stands for a bivariate distribution with the two independent marginal distributions each being the χ2(5) distribution. 













5. Discussion
If we have prior information that 


angle in the Royston test among six fixed angles 


comparable to the FA test in the bivariate case. Of course, combining SWT-based tests with other non-SWT type tests (e.g. the kurtosis test [18] - [20] ) might also worth consideration in order to obtain generally robust and powerful tests such as the combination test developed in [21] .
Acknowledgements
The authors would like to thank Dr. Ming Zhou and Dr. Jiqiang Guo for help with R programming and for constructive conversations. Y.S.’s research is partially supported by the NYU NIEHS Center Grant P30 ES00260 and the NYU Cancer Center Support Grant 2P30 CA16087.
References
- Thode Jr., H.C. (2012) Testing for Normality. Marcel Dekker, Inc., New York.
- Shapiro, S.S. and Wilk, M.B. (1965) An Analysis of Variance Test for Normality (Complete Samples). Biometrika, 52, 591-611. http://dx.doi.org/10.1093/biomet/52.3-4.591
- Royston, T.P. (1982) An Extension of Shapiro and Wilk W Test for Normality to Large Samples. Applied Statistics, 31, 115-124. http://dx.doi.org/10.2307/2347973
- Royston, T.P. (1983) Some Techniques for Assessing Multivarate Normality Based on the Shapiro-Wilk W. Applied Statistics, 32, 121-133. http://dx.doi.org/10.2307/2347291
- Royston, T.P. (1992) Approximating the Shapiro-Wilk W-Test for Non-Normality. Statistics and Computing, 2, 117- 119. http://dx.doi.org/10.1007/BF01891203
- Royston, J.P. (1995) Remark AS R94: A Remark on Algorithm AS 181: The W Test for Normality. Applied Statistics, 44, 547-551. http://dx.doi.org/10.2307/2986146
- Korkmaz, S. (2013) Royston’s H Test: Multivariate Normality Test. http://cran.r-project.org/web/packages/royston/index.html
- Villaseñor-Alva, J.A. and González-Estrada, G. (2009) A Generalization of Shapiro-Wilk’s Test for Multivariate Normality. Communications in Statistics-Theory and Methods, 38, 1870-1883. http://dx.doi.org/10.1080/03610920802474465
- Gonzalez-Estrada, G. and Villaseñor-Alva, J.A. (2013) Generalized Shapiro-Wilk Test for Multivariate Normality. http://rpackages.ianhowson.com/cran/mvShapiroTest/
- Fattorini, L. (1986) Remarks on the Use of the Shapiro-Wilk Statistic for Testing Multivariate Normality. Statistica, 46, 209-217.
- Henze, N. and Zirkler, B. (1990) A Class of Invariant Consistent Tests for Multivariate Normality. Communications in Statistics-Theory and Method, 19, 3595-3618. http://dx.doi.org/10.1080/03610929008830400
- Malkovich, J.F. and Afifi, A.A. (1973) On Tests for Multivariate Normality. Journal of American Statistical Association, 68, 713-718. http://dx.doi.org/10.1080/01621459.1973.10481358
- Mudholkar, G., Srivastava, D. and Lin, C. (1995) Some p-Variate Adaptations of the Shapiro-Wilk Test of Normality. Communications in Statistics-Theory and Method, 24, 953-985. http://dx.doi.org/10.1080/03610929508831533
- Srivastava, M. and Hui, T. (1987) On Assessing Multivariate Normality Based on Shapiro-Wilk W Statistic. Statistics and Probability Letters, 5, 15-18. http://dx.doi.org/10.1016/0167-7152(87)90019-8
- Shao, Y. and Zhou, M. (2010) A Characterization of Multivariate Normality through Univariate Projections. Journal of Multivariate Analysis, 101, 2637-2640. http://dx.doi.org/10.1016/j.jmva.2010.04.015
- Fisher, R.A. (1936) The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, 179-188. http://dx.doi.org/10.1111/j.1469-1809.1936.tb02137.x
- Looney, S.W. (1995) How to Use Tests for Univariate Normality to Assess Multivariate Normality. The American Statistician, 49, 64-70.
- Small, N. (1980) Marginal Skewness and Kurtosis in Testing Multivariate Normality. Applied Statistics, 29, 85-87. http://dx.doi.org/10.2307/2346414
- Mardia, K.V. (1974) Applications of Some Measures of Multivariate Skewness and Kurtosis in Testing Normality and Robustness Studies. Sankhyā: The Indian Journal of Statistics, Series B, 36, 115-128.
- Srivastava, M.S. (1984) A Measure of Skewness and Kurtosis and a Graphical Method for Assessing Multivariate Normality. Statistics and Probability Letters, 2, 263-267. http://dx.doi.org/10.1016/0167-7152(84)90062-2
- Zhou, M. and Shao, Y. (2014) A Powerful Test for Multivariate Normality. Journal of Applied Statistics, 41, 351-363. http://dx.doi.org/10.1080/02664763.2013.839637
Appendix: The R Code for Calculating the FA Test Statistic
“SW” <- function(X) shapiro.test(X)$statistic
“FA” <- function(X) {
X < - as.matrix(X)
n < - NROW(X)
p < - NCOL(X)
mu< - apply(X,2,mean)
nSinver< - solve((n-1)*cov(X))
Y < - X%*%t ((X-matrix(rep(mu,n),ncol=p,byrow=TRUE))%*%nSinver)
return(min(apply(Y,2,SW)))}
## END




