Open Journal of Statistics
Vol.05 No.01(2015), Article ID:54132,5 pages
10.4236/ojs.2015.51008
Statistical Models for Forecasting Tourists’ Arrival in Kenya
Albert Orwa Akuno1, Michael Oduor Otieno2, Charles Wambugu Mwangi1, Lawrence Areba Bichanga1
1Department of Mathematics, Egerton University, Egerton, Kenya
2Department of Mathematics and Computer Science, Laikipia University, Nyahururu, Kenya
Email: orwaakuno@gmail.com, mkaili91@yahoo.com, charlesmwangi@gmail.com, lawareba@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 January 2015; accepted 13 February 2015; published 16 February 2015
ABSTRACT
In this paper, an attempt has been made to forecast tourists’ arrival using statistical time series modeling techniques―Double Exponential Smoothing and the Auto-Regressive Integrated Moving Average (ARIMA). It is common knowledge that forecasting is very important in making future decisions such as ordering replenishment for an inventory system or increasing the capacity of the available staff in order to meet expected future service delivery. The methodology used is given in Section 2 and the results, discussion and conclusion are given in Section 3. When the forecasts from these models were validated, Double Exponential Smoothing model performed better than the ARIMA model.
Keywords:
Exponential Smoothing, ARIMA Model, Tourists’ Arrival Data

1. Introduction
Tourism is one of Kenya’s major foreign exchange earners. This greatly depends on the arrival of various groups of tourists. The forecast of tourists’ arrivals is important since it would enable the tourism related industries like airlines, hotels and other stakeholders to adequately prepare for any number of tourists at any future date. In this paper, an attempt has been made to forecast tourists’ arrivals using statistical time series modeling techniques―Double Exponential Smoothing and Auto-Regressive Integrated Moving Average (ARIMA). [1] used the same models to forecast milk production in India. [2] used univariate SARIMA models to forecast tourists’ demands in India.
Then data on tourists’ arrival in Kenya were obtained from the Ministry of East African Affairs, Commerce and Tourism, Department of Tourism. Tourists’ arrival for the period 1995 to 2008 was used for model fitting, and data for the remaining periods from 2009 to 2012 were used for model validation. The analysis was carried out using R-language, Excel and Minitab version 16.1.1.
2. Methodology
2.1. Selection of Appropriate Smoothing Techniques
Once the presence of trend is detected in the data, smoothing of the time series data follows. Various smoothing techniques as discussed by [3] include; Simple Exponential Smoothing (SES), Double Exponential Smoothing (
2.1.1. Simple Exponential Smoothing (SES)
For the series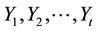 , the forecast for the preceding value
, the forecast for the preceding value , say
, say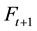 , is based on the weights
, is based on the weights 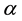 and
and 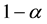 to the recent observation
to the recent observation 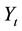 and forecast
and forecast 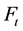 respectively, where
respectively, where 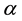 is the smoothing constant. The form of the model is
is the smoothing constant. The form of the model is
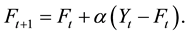 (1)
(1)
The size of 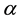 used has a great influence on the forecast. The best value of
used has a great influence on the forecast. The best value of 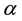 corresponding to the minimum mean square error (MSE) is usually used.
corresponding to the minimum mean square error (MSE) is usually used.
2.1.2. Double Exponential Smoothing (Holt’s)
The form of the model is
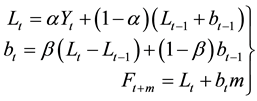 (2)
(2)
where 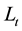 in the model is the level of the series at time
in the model is the level of the series at time 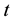 and
and 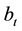 is the slope (Trend) of the series at time
is the slope (Trend) of the series at time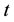 ,
, 









The pair of 

2.1.3. Triple Exponential Smoothing (Winter’s)
When time series data exhibit seasonality, Triple Exponential Smoothing method is the most recommendable. It incorporates three smoothing equations; first for the level, second for trend and third for seasonality.
2.2. Auto-Regressive Integrated Moving Average (ARIMA Model)
2.2.1. Model Identification
According to Box and Jenkins two graphical procedures are used to access the correlation between the observations within a single time series data. According to [5] , these devices are called an estimated autocorrelation func- tions and the estimated partial autocorrelation function. These two procedures measure statistical relationships within the time series data. Summarization of statistical correlation within the time series data is the other step in the identification. Box and Jenkins suggest a whole family of ARIMA models from which we may choose.
In choosing the model that seems appropriate we use the estimated ACF and PACF. This is due to the basic idea that every ARIMA model will have unique ACF and PACF associated with it. Thus we select the model whose theoretical ACF and PACF resembles the anticipated ACF and PACF of the time series data [6] .
2.2.2. Estimation
An estimate of the coefficients of the model is obtained by modified least squares method or the maximum likelihood estimation method suitable to the time series data.
2.2.3. Diagnostic Checking
Diagnostic checks help to determine if the anticipated model is adequate. At this stage, an examination of the residuals from the fitted model is done and if it fails the diagnostic tests, it is rejected and we repeat the cycle until an appropriate model is achieved.
The ARIMA model is obtained by taking 

Equation (3) is referred to as the ARIMA
Different combinations of AR and MA individually yield different ARIMA models [7] . The optimal model is obtained on the basis of minimum value of Akaike Information Criteria (AIC) given by

where 


where 


3. Results and Discussions
3.1. Exponential Smoothing Model
Table 1 shows the yearly tourists’ arrival in Kenya (in thousands) for the period 1995-2012. The time plot (Figure 1) revealed that there was increasing trend from the year 2002 to 2007. However, there was a sharp drop
Table 1. Data on tourists’ arrival in Kenya for the period 1995 to 2012.
Source: Ministry of East African affairs, Commerce and Tourism: Department of Tourism (Kenya).
in the number of tourists in the year 2008 followed by an increasing trend from the year 2009 to 2012. For smoothing the data, Holt’s Double Exponential Smoothing was used. Various combinations of 




where 


3.2. ARIMA Model
Figure 1 showed that the series was non-stationary since there was some trend component present. The data was made stationary by taking the first order difference
Using R-language for different values of 


The estimation of the model parameters was done by maximum likelihood estimation technique. The fitted model was then used to forecast tourists’ arrival from 2009 to 2012. The forecast values are shown in Table 3.
Table 2. Forecast of tourists’ arrival in Kenya using double exponential smoothing.
Figure 1. Time plot of tourists’ arrival in Kenya between 1995 and 2009.
Figure 2. Plot of differenced tourists’ arrival data.
Table 3. Forecast of tourists’ arrival in Kenya ARIMA (1, 1, 1) models.
Table 4. Forecast of tourists’ arrival in Kenya using double exponential smoothing and ARIMA (1, 1, 1) models.
3.3. Comparison and Conclusion of the Performance of the Two Models
Performance evaluation measures MAPE and the RMSE were obtained for the forecasted tourists’ arrivals for the years 2009 to 2012.
The comparison of the two models based on MAPE and RMSE is as given in Table 4. Based on the results from the table, Double Exponential Smoothing model was the best to forecast tourists’ arrival in Kenya as both its MAPE and RMSE values were least compared to those of ARIMA (1, 1, 1).
References
- Satya, P., Ramasubramanian, V. and Menta, S.C. (2007) Statistical Models for Forecasting Milk Production in India. Journal of the Indian Society of Agricultural Statistics, 61, 80-83.
- Padhan, P.C. (2011) Forecasting International Tourists Footfalls in India: An Assortment of Competing Models. International Journal of Business and Management, 6, 190-202.
- Gardener, E.S. (1985) Exponential Smoothing―The State of the Art. Journal of Forecasting, 4, 1-28. http://dx.doi.org/10.1002/for.3980040103
- Jani, P.N. (2014) Business Statistics: Theories and Applications. PHI Learning Private Limited, Delhi.
- Box, G.E.P. and Jenkins, G.M. (1970) Time Series Analysis: Forecasting and Control. Holden-Day, San Francisco.
- Pankratz, A. (1983) Forecasting with Univariate Box-Jenkins Models: Concepts and Cases. John Wiley and Sons, New York. http://dx.doi.org/10.1002/9780470316566
- Makridakis, S., Wheelwright, S.C. and Hyndman, R.J. (1998) Forecasting: Methods and Applications. John Wiley & Sons, New York.






