Received 4 August 2014; revised 9 September 2014; accepted 29 September 2014

ABSTRACT

The Goel-Okumoto software reliability model is one of the earliest attempts to use a non-homo- geneous Poisson process to model failure times observed during software test interval. The model is known as exponential NHPP model as it describes exponential software failure curve. Parameter estimation, model fit and predictive analyses based on one sample have been conducted on the Goel-Okumoto software reliability model. However, predictive analyses based on two samples have not been conducted on the model. In two-sample prediction, the parameters and characteristics of the first sample are used to analyze and to make predictions for the second sample. This helps in saving time and resources during the software development process. This paper presents some results about predictive analyses for the Goel-Okumoto software reliability model based on two samples. We have addressed three issues in two-sample prediction associated closely with software development testing process. Bayesian methods based on non-informative priors have been adopted to develop solutions to these issues. The developed methodologies have been illustrated by two sets of software failure data simulated from the Goel-Okumoto software reliability model.

Keywords:

Nonhomogeneous Poisson Process, Software Reliability Models, Non-Informative Priors, Bayesian Approach

1. Introduction

Software reliability is defined as the probability of failure free software operations for a specified period of time in a specified environment [1] . The reliability of any software is of great interest to the software developers before a decision is made to release the software into the market. Software developers need correct and concise information about how reliable software is before they decide to release the software into the market as single software defect can cause system failure and to avoid these failures, reliable software is required [2] . Software reliability is achieved through testing during the software development stage [3] . The usual way of removing bugs from a software system is by running test cases on the software system similar to the way users will operate it in their particular environment. However, the emulation of end-user environment during the test interval is difficult, expensive and time consuming especially when there are multiple types of end-users in different environments. Software reliability modeling can be used to address this dilemma especially when reliability testing on two software systems can be achieved in one testing period. Software reliability modeling can provide the basis for planning reliability growth tests, monitoring progress, estimating current reliability, forecasting and predicting future reliability improvements [4] . Predictive analyses help in conducting forecasting and prediction. A prediction interval is usually constructed to provide the time frame when the 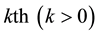future failure observation will occur with a pre-determined confidence level [5] .

An Exponential Nonhomogeneous Poisson Process with intensity function

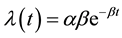(1)

is the earliest software reliability model to be developed. Such a model is a NHPP and is mostly referred to as the Goel-Okumoto (1979) software reliability model, after the researchers Goel and Okumoto who first introduced it in 1979.

The model described in Equation (1) is a software reliability model and has been applied to a number of software testing environments and its application and usefulness in describing and assessing software failures has been conducted by various authors. For instance, [6] used Kolmorgorov-Sminorv goodness-of-fit test for checking the adequacy of the software reliability model and they also presented they also presented software failure data which, after study, depicted that the failure rate, i.e. the number of failures per hour, seemed to be decreasing with time. One-sample Bayesian predictive analysis on the model has also been conducted, [7] . However, there is no literature on two-sample Bayesian predictive analyses on the model.

This paper therefore focuses on two-sample Bayesian predictive analyses on the model whose intensity function is described in Equation (1). First, three issues in two-sample predictions that may be experienced during the development testing stage of the software are identified and their corresponding predictive distributions are thereafter developed in Section 2. The main results for the two-sample prediction are presented in Section 3. The developed methodologies are illustrated in Section 6 using simulated two-software failure data. Discussion is given in Section 7 and finally, mathematical proofs are given in the Appendix.

2. Issues in Two-Sample Software Reliability Prediction

In this section, three issues associated closely with software development testing process are presented and their predictive distributions are developed using Bayesian approach. For the purposes of the three predictive issues, it is assumed that a reliability growth testing is performed on a software and the cumulative number of failures of the software in the time interval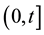, denoted by is observed. It is further assumed that 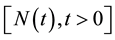follows the NHPP with intensity function given in Equation (1).

Let 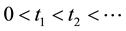be the observed failure times. Failure data is said to be failure-truncated when testing stops after a predetermined 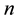number of failures occur. The 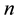failure times are denoted by 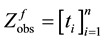where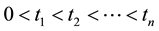. Failure data is said to be time truncated if testing stops at a predetermined time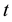. The corresponding observed failure data is denoted by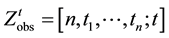, where . Now, let us consider two software systems and assume that their cumulative inter-failure times obey the Goel-Okumoto (1979) software reliability model with observed data being eithe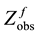r or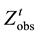. Based on 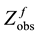or, we are interested in the following problems:

A1: How to predict the failure time of the second software system;

B1: How to predict the number of failures that will occur in the time interval for the second software system.

C1: How to predict the failure time of the second software system supposing that the number of failures in for the second software system is but the exact occurrence times are unavailable.

Posterior and Predictive Distributions

Let represent or. The joint density of is therefore

. (2)

Case 1: when the shape parameter is known, the following non informative prior distribution of is adopted

. (3)

Thus, the posterior distribution of is given by

. (4)

Let be the random variable being predicted. The posterior predictive distribution of is then given as

. (5)

Hence the Bayesian UPL of with level denoted as must satisfy

. (6)

3. Main Results for the Two-Sample Prediction

Proposition 1 (for issue A1)

The Bayesian UPL of (i.e. the failure time of the second software system) with level when is known is

. (7)

Proposition 2 (for issue B1)

The probability that the number of failures in the time interval for the second system does not exceed a pre-determined nonnegative integer, when is known is

. (8)

Proposition 3 (for issue C1)

Given that the number of failures in for the second software is, the Bayesian UPL of with level is satisfying the equation

. (9)

4. Data Simulation

In this section, two software failure data sets are generated from the Goel-Okumoto (1979) software reliability model. The two data sets are simulated using the same model and parameters. The simulated data is used to illustrate the methodologies developed for the two sample Bayesian predictive analyses. The simulation procedure was as follows. The Goel-Okumoto (1979) model is as given in Equation (1).

The values of and were fixed. A value of from the set was selected. The study used T = 200. The simulation used in the study is for illustrative purposes only. Nevertheless, there is a practical interpretation to the choices of and. Case studies e.g. [8] have shown that a software fault density at the system testing stage is frequently on the order of five bugs per 1000 lines of code. The choice of α = 100 could be thought of as symbolizing a practically large software system that is on the order of 20,000 lines of codes. The choices for and together imply that most of the failures will be discovered during the simulated test period. Following the forgoing discussion, the following steps were used to simulate two data sets from the Goel-Okumoto (1979) software reliability model:

Step 1:.

Step 2: Generate a random number.

Step 3:, if, stop.

Step 4: Generate a random number U.

Step 5: If, set,.

Step 6: Go to step 2.

In the above steps, is known as the intensity function and is such that. the last value of represents the number of events time, and are the event times. The above procedure of simulation is referred to as the thinning algorithm since it ‘thins’ the homogeneous Poisson points. It is the most efficient simulation procedure in the sense that it has the fewest number of rejected events times when is near throughout the interval [9] . Using the above procedure, the following two data sets were generated. The first data set is assumed to be the software failure times from the first software and the second data set is assumed to be the failure times from the second software.

Software one: 8.9345, 27.0177, 34.5816, 54.8606, 83.5715, 111.4006, 139.8851, 157.4743, 181.0868, 182.8410.

Software two: 2.3159, 16.2530, 20.5721, 23.3416, 42.8030, 46.7417, 61.0926, 63.8807, 75.1330, 80.7768, 97.3435, 117.9091, 129.3157, 138.0590, 169.3410, 172.7516, 186.0293, 193.1918, 198.5999.

5. Maximum Likelihood Estimation

Suppose the observation of the failure times occurred in the time interval where T = 200, and faults were observed at the failure times. The joint density of the failure times is as in Equation (2). Taking the log-likelihood function of Equation (2) gives

. (10)

Differentiating with respect to and and equating to zero gives

(11)

. (12)

Solving Equation (11) and Equation (12) we obtain

(13)

. (14)

A necessary and sufficient condition for Equation (13) and Equation (14) to have a unique and positive solution is that, [10] . That is, the ML estimates of and will exist only and only if

two times the mean failure time is less than. In most cases, the precision in the difference in the denominator of the second part in the RHS of Equation (14) will be poor since will always be very close to unity. This brings a numerical difficulty in finding the root of Equation (14). An alternative form of Equation (14) that overcomes this difficulty is

. (15)

A numerical procedure known as the Newton Raphson method can be used to solve Equation (13) and Equation (15). The Newton Raphson method requires choosing of initial values of and. Consequently, α = 95 and were chosen as the initial values. There is no any other explanation to the choosing of the initial values other than the fact that they are very close to the values α = 100 and that were used during the simulation of the two software failure data sets in Section 4.6. Consequently, the ML estimates and for software one were obtained.

6. Real Example for Two-Sample Bayesian Prediction

Here, we use the two software data sets simulated in Section 4.6 to illustrate the developed propositions in Section 4.4 for two sample Bayesian prediction problems. Assuming that the two software systems were observed in the time interval, and their successive failure times are given by:

Software one: 8.9345, 27.0177, 34.5816, 54.8606, 83.5715, 111.4006, 139.8851, 157.4743, 181.0868, 182.8410.

Software two: 2.3159, 16.2530, 20.5721, 23.3416, 42.8030, 46.7417, 61.0926, 63.8807, 75.1330, 80.7768, 97.3435, 117.9091, 129.3157, 138.0590, 169.3410, 172.7516, 186.0293, 193.1918, 198.5999.

The two software failure times are simulated from the same Goel-Okumoto (1979) software reliability model. The three issues in the two sample prediction in chapter three are addressed as follows:

Issue A2: First, we assume that the failure times of the second software were not observed. Based on the failure data of software one, the maximum likelihood estimate of is given by 0.001022177. When is known to be 0.001022177, and from Equation (7), the Bayesian UPL for the failure time of the second software with level is such that

.

Issue B2: if, then from Equation (8), the probability that the number of failures in the time interval for the second software not exceeding a pre-determined nonnegative integer, is.

Issue C2: suppose that the number of observed failures of the second software during is. Based on the failure data of the second software, if, then from Equation (9), the Bayesian UPL for with level is

7. Discussion

Several issues may arise during development testing of a software system especially when the Goel-Okumoto (1979) software reliability model has been used to model the failure process of the software system. This paper has provided solutions to three issues associated closely with software development testing process. Bayesian approach with non-informative prior has been used to address the three issues. Explicit solutions to the issues have been obtained. These solutions may prove useful to software engineers in determining when to modify, debug and terminate the software development testing process.

Non-informative prior has been used in this paper to develop the methodologies to the said three issues. However, informative priors may also prove useful in deriving the methodologies. We leave this open for future research. Further, this paper has only derived the methodologies for known shape parameter. It may be interesting to derive solutions for the same problems for the case when the shape parameter is unknown. The procedures presented in this paper can also be extended to other NHPPs such as the Musa-Okumoto process, the delayed S-shaped process and the Cox-Lewis process.

References

Appendix (Proofs of Proposition 1-3)

The following identity is used in proving some of the propositions. The identity is given without proof.

(A.1)

where is any positive integer, and are two real numbers is an increasing and differentiable function, and.

Proof of Proposition 1

We know that given, the failure times have the same distribution as the order statistics corresponding to independent random variables with density, which reduces to. This implies that. This is to say that. Consequently,

. (A.2)

The joint density of is also given by Equation (2). Equation (2) divided by Equation (A.2) yields the density of and we have

(A.3)

Replacing by, for the second system, we have the density of being given as

. (A.4)

From Equation (5) and Equation (A.4) we have

(A.5)

From Equation (6) and Equation (A.5), we have

. (A.6)

Equation (A.6) implies the formula in Equation (7) .

Proof of Proposition 2

The study is interested in predicting the number of failures (denoted by) of the second system occurring in the time interval. Obviously,

. (A.7)

For any level, the Bayesian Upper prediction limit for is satisfying

.

Here, an equivalent problem is considered. For any given positive integer, we want to compute the probability that i.e.

. (A.8)

When is known, from Equation (A.7) and Equation (4) we have

. (A.9)

Rearranging Equation (A.9) we obtain

. (A.10)

Equation (A.9) implies the formula in Equation (8) .

Proof of Proposition 3

First, we want to find the conditional density of given, from Equation (2),

. (A.11)

After integrating Equation (A.11) with respect to we obtain

. (A.12)

Further integrating Equation (A.12) with respect to, yields

. (A.13)

Therefore, the conditional density of given is

(A.14)

Which is independent of. When is known, Equation (5) can be re-written as

where is given by Equation (A.14) and

is given by Equation (4). Hence.

Given, the Bayesian UPL of with level is such that

. (A.15)

If, Equation (A.15) becomes

. (A.16)

Solving the integral part of Equation (A.16), we obtain

. (A.17)

Thus, the Bayesian UPL of with confidence level is that satisfies Equation (A.17).