Open Journal of Statistics
Vol.4 No.5(2014), Article ID:49084,10 pages
DOI:10.4236/ojs.2014.45039
One-Sample Bayesian Predictive Analyses for an Exponential Non-Homogeneous Poisson Process in Software Reliability
Albert Orwa Akuno, Luke Akong’o Orawo, Ali Salim Islam
Department of Mathematics, Egerton University, Egerton, Kenya
Email: orwaakuno@gmail.com, orawo2000@yahoo.com, asislam54@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 May 2014; revised 28 June 2014; accepted 12 July 2014
Abstract
The Goel-Okumoto software reliability model, also known as the Exponential Nonhomogeneous Poisson Process, is one of the earliest software reliability models to be proposed. From literature, it is evident that most of the study that has been done on the Goel-Okumoto software reliability model is parameter estimation using the MLE method and model fit. It is widely known that predictive analysis is very useful for modifying, debugging and determining when to terminate software development testing process. However, there is a conspicuous absence of literature on both the classical and Bayesian predictive analyses on the model. This paper presents some results about predictive analyses for the Goel-Okumoto software reliability model. Driven by the requirement of highly reliable software used in computers embedded in automotive, mechanical and safety control systems, industrial and quality process control, real-time sensor networks, aircrafts, nuclear reactors among others, we address four issues in single-sample prediction associated closely with software development process. We have adopted Bayesian methods based on non-informative priors to develop explicit solutions to these problems. An example with real data in the form of time between software failures will be used to illustrate the developed methodologies.
Keywords: Nonhomogeneous Poisson Process, Non-Informative Priors, Software Reliability Models, Bayesian Approach

1. Introduction
Over the last decade of the 20th century and the first few years of the
21st century, the demand for complex software systems has gone high as
it is seen that today, computers are embedded in automotive mechanical and safety
control systems, industrial and quality process control, real-time sensor networks,
aircrafts, nuclear reactors, hospital healthcare and air traffic control systems
among others; computer systems have become an indispensable component of our modern
society today. Consequently, the reliability of software used in these systems has
been a major concern and a requirement in the modern generation. Software reliability
is defined as the probability of failure-free software operations for a specified
period of time in a specified environment [1] .
A single software defect can cause system failure and to avoid these failures, reliable
software is required. Software reliability is achieved through testing during the
software development testing stage [2] . The usual
criteria of removing bugs in software are by running test cases in a manner that
exercises the software similar to the way that users will operate in their particular
environment. However, emulating end-user environment during the test interval is
difficult and time-consuming especially when there are multiple types of end-users
and also, business pressure to release a software system within a tight market window
puts a constraint on the amount of time that can be spent testing the software.
Software reliability modeling comes in handy to address this dilemma. As indicated
by [3] , software reliability modeling can provide
the basis for planning reliability growth tests, monitoring progress and estimating
current reliability and forecasting and predicting future reliability improvements.
Forecasting and prediction are achieved through predictive analyses. In particular,
predictive analyses are useful in determining when to terminate the development
process of software or hardware. Often, a prediction interval is constructed to
provide the time frame when the
 future failure observation will occur with a pre-determined confidence level [4] .
future failure observation will occur with a pre-determined confidence level [4] .
Many software reliability models have been developed by various authors and researchers in the past three decades. Amongst, an Exponential Nonhomogeneous Poisson Process with intensity function
 (1)
(1)
is the earliest software reliability model to be developed by Goel and Okumoto in 1979. In various literatures, this NHPP is called the Goel-Okumoto (1979) model.
As noted by [5] , the Goel-Okumoto (1979) model
has been applied to a number of software testing environments and its application
on assessing and detecting software failures has been investigated by various authors.
For instance, the Goel-Okumoto model has been used to develop a statistical control
mechanism that could be used to detect whether a software process is statistically
under control or not. ML estimation of the parameters of the Goel-Okumoto (1979)
model has been conducted and in particular, it has been shown that the ML estimates
of the parameters of the model are not consistent as the testing period extends
to infinity. [6] presented an empirical method
for selecting software reliability growth models for release decision-making where
they applied iteratively various software reliability models namely Goel-Okumoto
(1979), Delayed S-shaped, Gompertz and Yamada exponential software reliability growth
models to weekly cumulative software failure data during system test to determine
the number of remaining failures expected in software after release. [7] also performed parameter estimation of the Goel-Okumoto,
Yamada S-shaped and Inflection S-shaped software reliability growth models where
they also established a necessary and sufficient condition with respect to the software
failure data, of which, if satisfied, will ensure that the MLE method returns a
unique positive and finite estimation of the unknown parameters of the Goel-Okumoto
and the Yamada S-shaped models. [8] presented software
failure data which, after study, depicted that the failure rate, i.e. the number
of failures per hour, seemed to be decreasing with time, an indication that a Nonhomogeneous
Poisson Process with mean value function

 , a mean value function corresponding to that
of the Goel-Okumoto software reliability model, was a reasonable model to describe
the failure process. From the literature, it is evident that most of the study that
has been done on the Goel-Okumoto software reliability model is parameter estimation
using, especially, the MLE method and model fit. There is a conspicuous absence
of literature on both the classical and Bayesian predictive analyses on the model.
, a mean value function corresponding to that
of the Goel-Okumoto software reliability model, was a reasonable model to describe
the failure process. From the literature, it is evident that most of the study that
has been done on the Goel-Okumoto software reliability model is parameter estimation
using, especially, the MLE method and model fit. There is a conspicuous absence
of literature on both the classical and Bayesian predictive analyses on the model.
This paper focuses on single-sample predictive inference for the Goel-Okumoto (1979) software reliability model using Bayesian approach. We first identify four issues in the single-sample prediction associated closely with the development testing process of software and proceed to develop and derive the corresponding predictive distributions in Section 2. The main results for single-sample prediction are presented in Section 3. A real example in the form of secondary software failure data in the form of execution times between successive software failures is used to illustrate the proposed and developed methodologies in Section 4. A discussion is given in Section 5 and thereafter, mathematical proofs are given in the Appendix.
2. Predictive Issues and Bayesian Method
During the development testing stage of a software, statisticians and engineers
are overly interested in various predictive problems whose solutions are believed
to be very important in modifying, debugging and determining when to terminate software
development testing process. In this section, we present four issues associated
closely with software development testing process and derive the predictive distributions
using Bayesian approach. For the purposes of the four predictive issues, we assume
that a reliability growth testing is performed on a software and the cumulative
number of failures of the software in the time interval , denoted by
, denoted by
 is observed. We further assume that
is observed. We further assume that
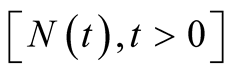 follows the NHPP with intensity function given in Equation (1). Let
follows the NHPP with intensity function given in Equation (1). Let
 be the observed failure times. Failure data is said to be failure-truncated when
testing stops after a predetermined n number of failures occur. We denote the n
failure times by
be the observed failure times. Failure data is said to be failure-truncated when
testing stops after a predetermined n number of failures occur. We denote the n
failure times by
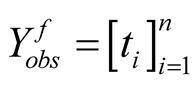 where
where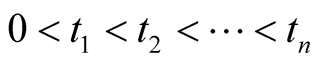 . Failure data is said to be time truncated
if testing stops at a predetermined time t. We denote the corresponding observed
failure data by
. Failure data is said to be time truncated
if testing stops at a predetermined time t. We denote the corresponding observed
failure data by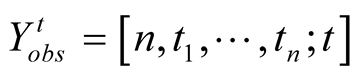 , where
, where .
.
Prediction interval is a confidence interval for a future observation or a function
of some future observations. Specifically, a double-sided (bilateral) prediction
interval for
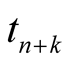 with confidence level
with confidence level
 is defined by
is defined by
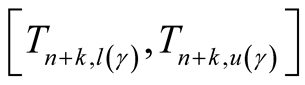 such that
such that . Similarly, a single-sided
(unilateral) lower or upper prediction limit for
. Similarly, a single-sided
(unilateral) lower or upper prediction limit for
 with level
with level
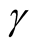 is defined by
is defined by
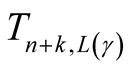 (or
(or ) which satisfies
) which satisfies
 (or
(or ). Both
). Both
 and
and
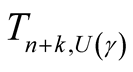 depends only on a single sample (or a single software) and are called single-sample
prediction limits. Prediction limits involving two samples (or two softwares) can
be defined similarly and are called two-sample prediction limits.
depends only on a single sample (or a single software) and are called single-sample
prediction limits. Prediction limits involving two samples (or two softwares) can
be defined similarly and are called two-sample prediction limits.
2.1. Issues in Single-Sample Software Reliability Prediction
Here, we consider one software and assume that its cumulative inter-failure times
obey the Goel-Okumoto (1979) software reliability model with observed data being
either
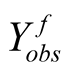 or
or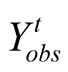 . Based on
. Based on
 or
or , we are interested in the following problems:
, we are interested in the following problems:
Issue A: what is the probability that at most k software failures will occur in
the future time period
 with
with ?
?
Issue B: suppose that the pre-determined target value
 for the failure rate of the software undergoing development testing is not achieved
at time T, what is the probability that the target value
for the failure rate of the software undergoing development testing is not achieved
at time T, what is the probability that the target value
 will be achieved at time
will be achieved at time ?
?
Issue C: suppose that the target value
 for the software failure rate is not achieved at time T, how long will it take so
that the software failure rate will be attained at
for the software failure rate is not achieved at time T, how long will it take so
that the software failure rate will be attained at ?
?
Issue D: what is the upper prediction limit (UPL) of
 with level
with level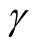 ,
,
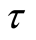 being a predetermined value greater than T?
being a predetermined value greater than T?
2.2. Posterior and Predictive Distributions
Let
 represent
represent
 or
or . The joint density of
. The joint density of
 is therefore
is therefore
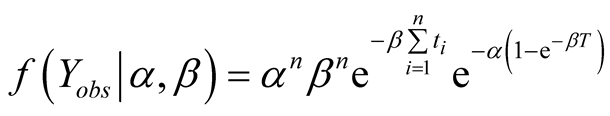 (2)
(2)
Case 1: When the shape parameter
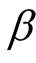 is known, we adopt the following non-informative prior distribution of
is known, we adopt the following non-informative prior distribution of :
:
 . (3)
. (3)
The posterior distribution of
 is thus given by
is thus given by
 (4)
(4)
Let
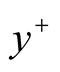 be the random variable being predicted. Then the posterior predictive distribution
of
be the random variable being predicted. Then the posterior predictive distribution
of
 is give as
is give as
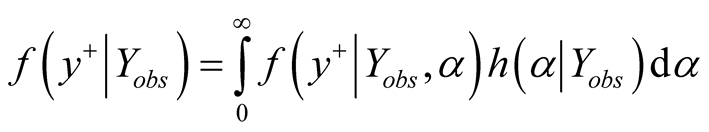 (5)
(5)
Hence the Bayesian UPL of
 with level
with level
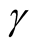 denoted as
denoted as
 must satisfy
must satisfy
 . (6)
. (6)
Case 2: When the shape parameter
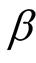 is unknown, we consider the following non-informative joint prior density for
is unknown, we consider the following non-informative joint prior density for
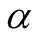 and
and
 (we assume that
(we assume that
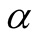 and
and
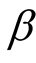 are independent).
are independent).
 (7)
(7)
Hence the corresponding joint posterior density is given as
 (8)
(8)
where
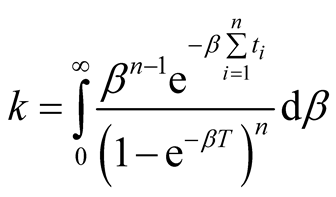 . (9)
. (9)
Similar to Equation (5) and Equation (6), let
 denote the Bayesian UPL of
denote the Bayesian UPL of
 with level
with level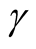 , then
, then
 (10)
(10)
and
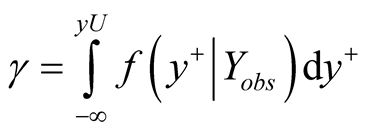 (11)
(11)
3. Main Results for the Prediction Problems
In this section, we address the four single-sample prediction issues raised in Section
2.1 using Bayesian approach. The following propositions are considered as the main
results with proofs being given in the Appendix. In the subsequent results, we use
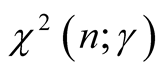 to represent the
to represent the
 percentage point of the chi-square distribution with n degrees of freedom and we
also assume the priors to be Equation (3) and Equation (7).
percentage point of the chi-square distribution with n degrees of freedom and we
also assume the priors to be Equation (3) and Equation (7).
Proposition 1 (for issue A): The probability that at most k software failures will
occur in the future time period
 with
with
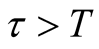 is
is
 (12)
(12)
Proposition 2 (for issue B): Suppose that the pre-determined target value
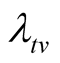 for the failure rate of the software undergoing development testing is not achieved
at time T, the probability that the target value
for the failure rate of the software undergoing development testing is not achieved
at time T, the probability that the target value
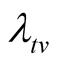 will be achieved at time
will be achieved at time
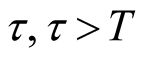 is
is
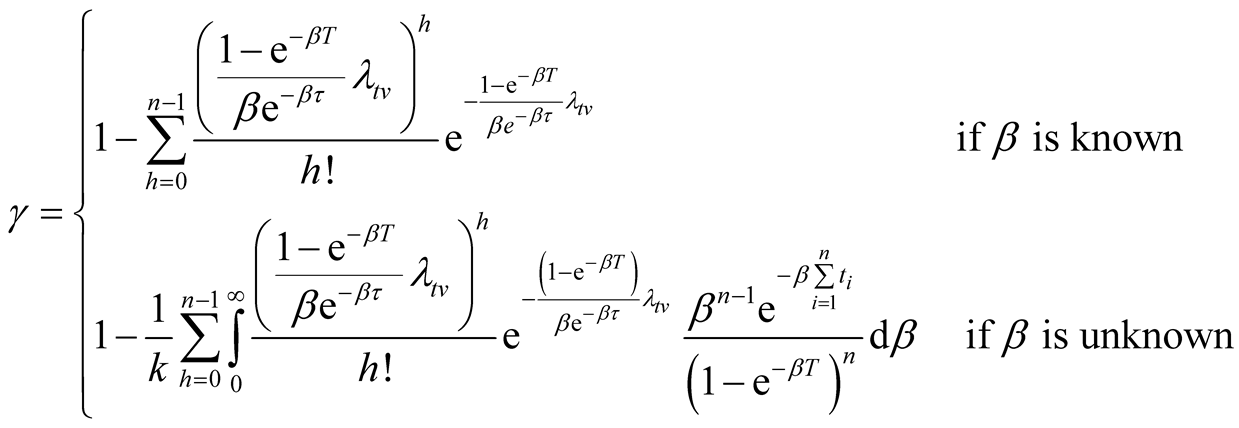 (13)
(13)
Remark 1: Let
 be i.i.d. sample from
be i.i.d. sample from , we can approximate
the second part of (13) via MCMC method.
, we can approximate
the second part of (13) via MCMC method.
Proposition 3 (for issue C): For given level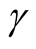 , the time
, the time
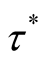 required to attain
required to attain
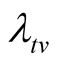 is
is
(i)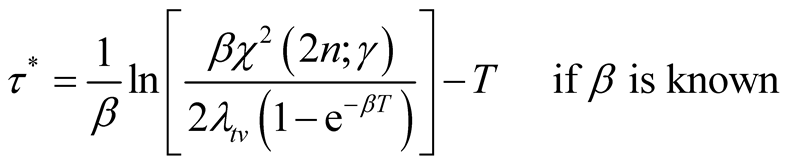 (14)
(14)
(ii) (15)
(15)
where
 is the solution to the following equation:
is the solution to the following equation:
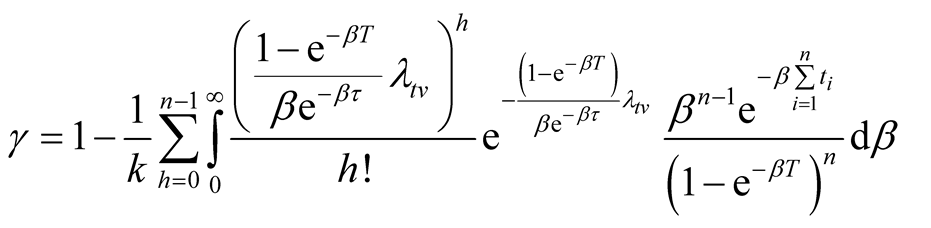 (16)
(16)
Proposition 4 (for issue D): The Bayesian UPL of
 with level
with level
 is
is
(i) (17)
(17)
(ii) ( unknown)
unknown)
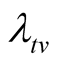 such that (18)
such that (18)
 (19)
(19)
4. Example
In this section, a real example from the time between failure data given by [9] is used to illustrate the developed methodologies for the single-sample Bayesian predictive analysis. The Table 1 gives the Time Between Failure.
The study has used the cumulative time between failures as failure times
 where
where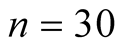 . These data obey the Goel-Okumoto (1979) software
reliability model [10] . The MLEs of the parameters
of the software reliability model based on the data are
. These data obey the Goel-Okumoto (1979) software
reliability model [10] . The MLEs of the parameters
of the software reliability model based on the data are
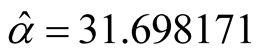 and
and . In the illustration of the developed methodologies,
the study has used these MLEs.
. In the illustration of the developed methodologies,
the study has used these MLEs.
1) Suppose that we are interested in the probability
 that at most k failures will occur in the future time period
that at most k failures will occur in the future time period
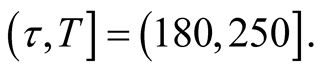 a) When
a) When
 is known (say
is known (say ), using the first formula
in Equation (12), we have
), using the first formula
in Equation (12), we have ,
,
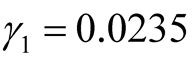 ,
,
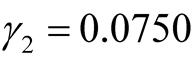 ,
,
 ,
,
 ,
,
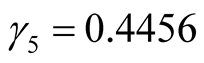 ,
,
 ,
,
 0.7193,
0.7193,
 ,
,
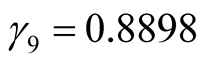 ,
,
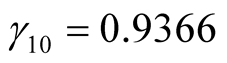 ,
,
 ,
,
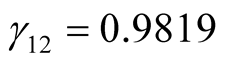 ,
,
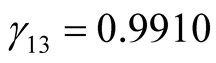 ,
,
 and
and
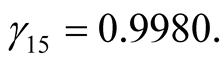 b) When
b) When
 is unknown, from the second formula in Equation (12) we obtain,
is unknown, from the second formula in Equation (12) we obtain,
 ,
,
 ,
,
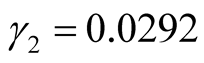 ,
,
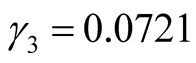 ,
,
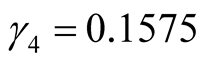 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
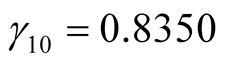 ,
,
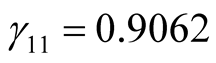 ,
,
 ,
,
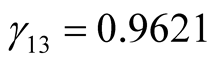 ,
,
 ,
,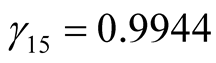 .
.
Figure 1 shows the graph of the desired probabilities
for the case when
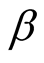 is known and when
is known and when
 is unknown.
is unknown.
2) Suppose that the target value is given by . At time
. At time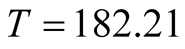 , the MLE of the achieved
failure rate for this software is
, the MLE of the achieved
failure rate for this software is
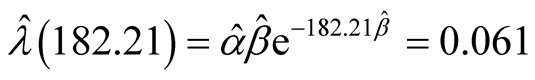 which is greater than
which is greater than
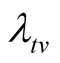 i.e. it cannot be achieved at time
i.e. it cannot be achieved at time . Thus the development
testing will continue. Suppose we want to predict the probability that the target
value
. Thus the development
testing will continue. Suppose we want to predict the probability that the target
value
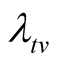 will be achieved at time
will be achieved at time . a) When
. a) When
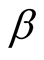 is known, say
is known, say , from the first formula
in Equation (13) we obtain
, from the first formula
in Equation (13) we obtain . Thus we can conclude
that the target value (failure rate) will not be achieved. b) When
. Thus we can conclude
that the target value (failure rate) will not be achieved. b) When
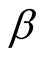 is unknown, from the second formula in Equation (13) and Remark 1, we obtain
is unknown, from the second formula in Equation (13) and Remark 1, we obtain
 where the Monte Carlo sample size is
where the Monte Carlo sample size is .
.
Table 1. Time between failures data.

Figure 1. Comparison of the probabilities γk that at most k failures will occur in the time interval (180, 240] for the cases of known and unknown β.
3) Since the target value
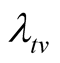 was not achieved at time
was not achieved at time , we want to know how long
it will require in order to attain
, we want to know how long
it will require in order to attain . a) When
. a) When
 is known (i.e.
is known (i.e.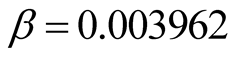 ), let
), let , from Equation (14)
we obtain
, from Equation (14)
we obtain . In other words, it will
take another 268.6116h in order to achieve the desired failure rate. b) When
. In other words, it will
take another 268.6116h in order to achieve the desired failure rate. b) When
 is unknown, from Equation (15) and Equation (16), we obtain
is unknown, from Equation (15) and Equation (16), we obtain . In other words, it will take another
770.79 h in order to achieve the desired failure rate when
. In other words, it will take another
770.79 h in order to achieve the desired failure rate when
 is unknown.
is unknown.
4) Given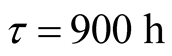 , a) when
, a) when
 is known, from Equation (17), the Bayesian Upper Prediction Limit of
is known, from Equation (17), the Bayesian Upper Prediction Limit of
 with level 0.90 is given by
with level 0.90 is given by
 b) When
b) When
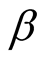 is unknown, from Equation (18) and Equation (19), the Bayesian UPL of
is unknown, from Equation (18) and Equation (19), the Bayesian UPL of
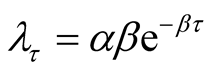 with level 0.90 is given by
with level 0.90 is given by .
.
5. Discussion
Several prediction problems arise during the development of any software especially when the Goel-Okumoto (1979) software reliability model is used to model the failure process. We have used Bayesian approach with non-informative priors to address some of the prediction problems that may arise during software development testing stage. We have obtained explicit solutions to these problems, which may prove useful for the modification, debugging and for the decision to terminate the development testing process of the software.
The adoption of Bayesian approach for the derivation of the solutions is advantageous in that the approach is available for cases of small sample sizes [11] [12] . Another advantage of the Bayesian approach is that it allows the input of prior information about the reliability growth process and provides full posterior and predictive distributions.
In this paper, we have used non-informative priors to derive the methodologies to address the said prediction problems. However, informative priors can similarly be used in place of non-informative priors. The same procedures presented in this paper can also be applied to other NHPPs such as the delayed S-shaped process and the Cox-Lewis process.
References
- Nuria, T.R. (2011) Stochastic Comparisons and Bayesian Inference in Software Reliability. Ph.D. Thesis, Universidad Carlos III de Madrid, Madrid.
- Daniel, R.J. and Hoang, P. (2001) On the Maximum Likelihood Estimates for the Goel-Okumoto Software Reliability Model. The American Statistician, 55, 219-222. http://dx.doi.org/10.1198/000313001317098211
- Meth, M. (1992) Reliability Growth Myths and Methodologies: A Critical View. Proceedings of the Annual Reliability and Maintainability Symposium, New York, 21-23 January 1992, 230-238.
- Yu, J.-W., Tian, G.-L. and Tang, M.-L. (2007) Predictive Analyses for Nonhomogeneous Poisson Processes with Power Law Using Bayesian Approach. Computational Statistics & Data Analysis, 51, 4254-4268.http://dx.doi.org/10.1016/j.csda.2006.05.010
- Kapur, P.K., Pham, H., Gupta, A. and Jha, P.C. (2011) Software Reliability Assessment with OR Applications. Springer Series in Reliability Engineering, Springer-Verlag London Limited, London. http://dx.doi.org/10.1007/978-0-85729-204-9
- Stringfellow, C. and Amschler, A.A. (2002) An Empirical Method for Selecting Software Reliability Growth Models. Empirical Software Engineering, 7, 319-343. http://dx.doi.org/10.1023/A:1020515105175
- Meyfroyt, P.H.A. (2012) Parameter Estimation for Software Reliability Models. Ph.D. Thesis, Universidad Carlos III de Madrid, Madrid.
- Razeef, M. and Mohsin, N. (2012) Software Reliability Growth Models: Overview and Applications. Journal of Emerging Trends in Computing and Information Sciences, 3, 1309-1320.
- Xie, M., Goh, T.N. and Ranjan, P. (2002) Some Effective Control Chart Procedures for Reliability Monitoring. Reliability Engineering and System Safety, 77, 143-150. http://dx.doi.org/10.1016/S0951-8320(02)00041-8
- Satya, P., Bandla, S.R. and Kantham, R.R.L. (2011) Assessing Software Reliability Using Inter Failures Time Data. International Journal of Computer Applications, 18, 975-978.
- Phillips, M.J. (2000) Bootstrap Confidence Regions for the Expected ROCOF of a Repairable System. IEEE Transactions on Reliability, 49, 204-208. http://dx.doi.org/10.1109/24.877339
- Quigley, J. and Walls, L. (2003) Confidence Intervals for Reliability-Growth Models with Small Sample-Sizes. IEEE Transactions on Reliability, 52, 257-262. http://dx.doi.org/10.1109/TR.2003.811865
Appendix (Proofs of Propositions 1 - 4)
In order to prove the propositions, we first give an identity without proof. The identity is
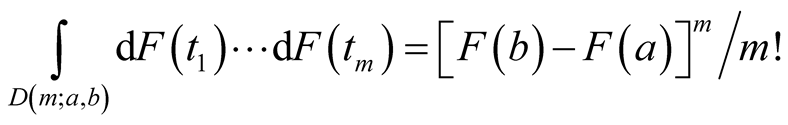 (A.1)
(A.1)
where m is any positive integer, a and b are two real numbers ,
,
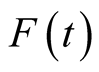 is an increasing and differentiable function,
and
is an increasing and differentiable function,
and

Proof of Proposition 1: The probability that at most k failures will occur in the
interval
 is
is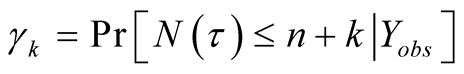 . When
. When
 is known, we have
is known, we have
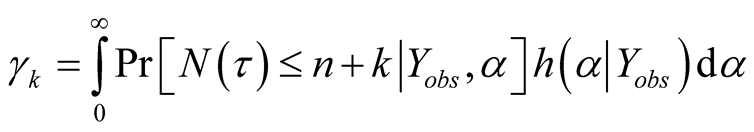 (A.2)
(A.2)
where
 is given by Equation (4) and
is given by Equation (4) and
 (A.3)
(A.3)
From Equation (2) we have
 and
and

 (A.4)
(A.4)
Hence (A.3) becomes
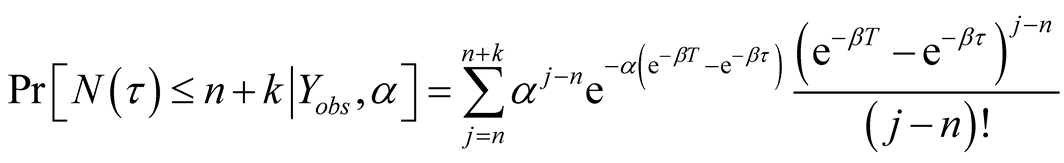 (A.5)
(A.5)
And (A.2) becomes
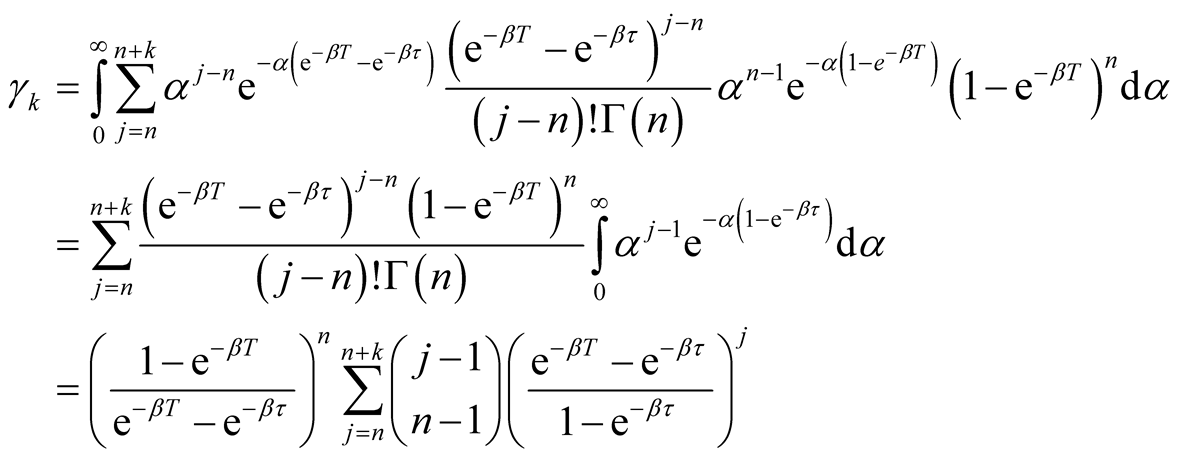 (A.6)
(A.6)
Equation (A.6) implies the first formula of Equation (12).
When
 is unknown, noting that
is unknown, noting that
 and
and
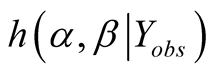 are given by Equation (A.3) and Equation (8) respectively, we have
are given by Equation (A.3) and Equation (8) respectively, we have
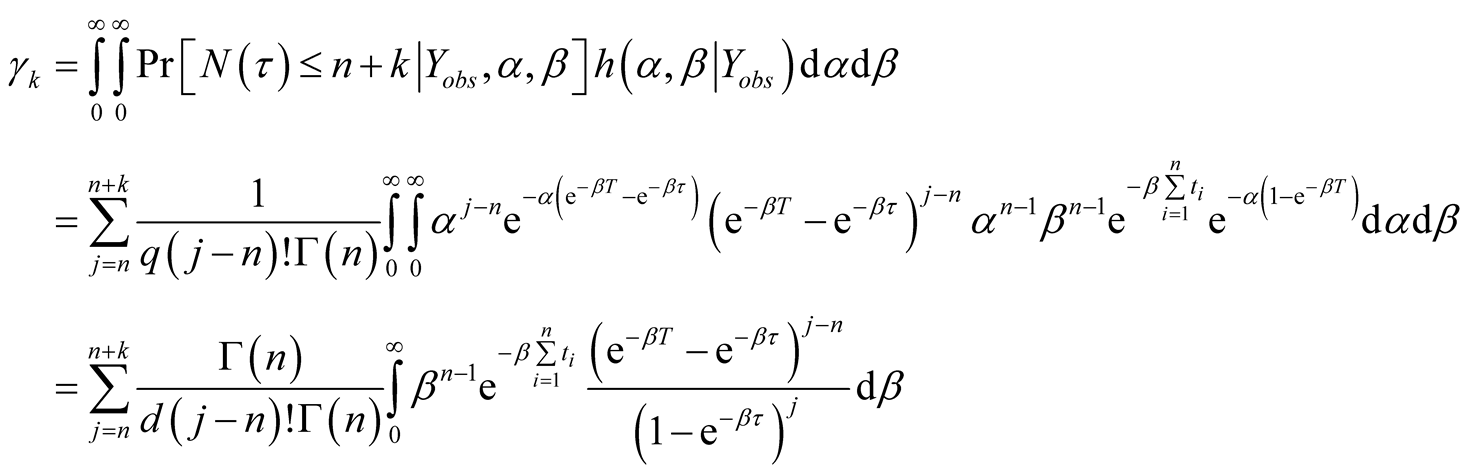 (A.7)
(A.7)
Equation (A.7) implies the second formula of Equation (12).
Proof of Proposition 2: Let
 denote the posterior density of
denote the posterior density of . Hence the probability
that the target value
. Hence the probability
that the target value
 will be achieved at time
will be achieved at time

 is given by
is given by
 . (A.8)
. (A.8)
When
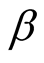 is known, making the transformation
is known, making the transformation
 , we have
, we have
 and
and . Consequently, the posterior density of
. Consequently, the posterior density of
 is
is . This implies that
. This implies that
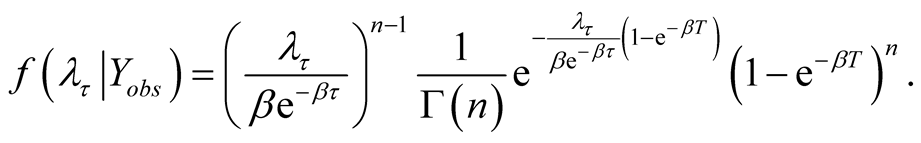
 which after simplification reduces to
which after simplification reduces to
 (A.9)
(A.9)
We note that
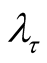 from Equation (A.9) follows a gamma distribution with parameters n and
from Equation (A.9) follows a gamma distribution with parameters n and
 Noting the relationship between gamma and Poisson distributions as
Noting the relationship between gamma and Poisson distributions as
 (A.10)
(A.10)
and from Equations (A.8), (A.9) and (A.10), we obtain the first formula of Equation (13).
When
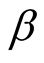 is unknown, making the transformation
is unknown, making the transformation
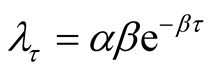 and
and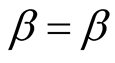 , we obtain
, we obtain
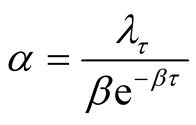 and
and . Note that the Jacobian is
. Note that the Jacobian is
 . From Equation (8), the joint posterior density
of
. From Equation (8), the joint posterior density
of
 is given as
is given as
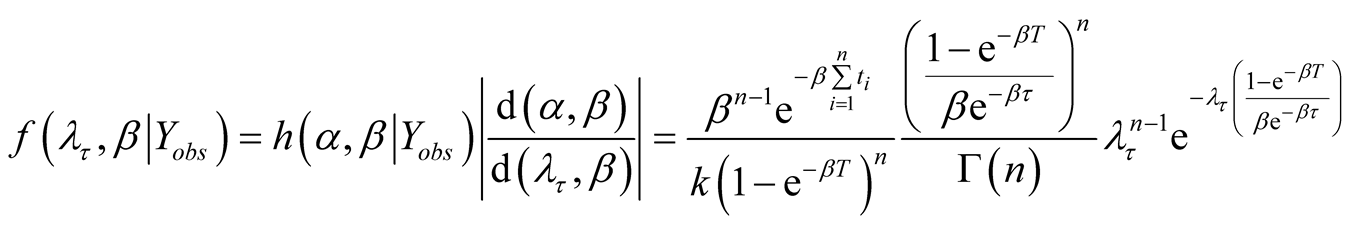 (A.11)
(A.11)
From Equation (A.8), Equation (A.10) and Equation (A.11) we obtain
 (A.12)
(A.12)
Equation (A.12) implies the second formula of Equation (13).
Proof of Proposition 3: For given level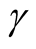 , the time required
to attain the target value
, the time required
to attain the target value
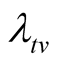 is
is
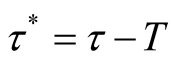 where
where
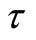 satisfies Equation (A.8). When
satisfies Equation (A.8). When
 is known, from Equation (A.9), it can easily be seen that
is known, from Equation (A.9), it can easily be seen that
 follows a chi-square distribution with
follows a chi-square distribution with
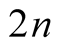 degrees of freedom. Therefore, we have
degrees of freedom. Therefore, we have
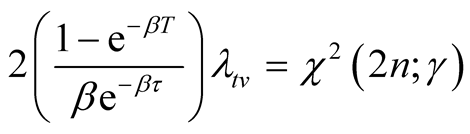 (A.13)
(A.13)
and Equation (14) follows immediately. We can obtain (ii) by following similar arguments given in the proof for the second part of Proposition 2.
Proof of Proposition 4: For a pre-determined

 , the Bayesian Upper Prediction Limit (UPL)
for
, the Bayesian Upper Prediction Limit (UPL)
for
 with level
with level
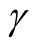 is
is
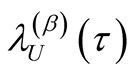 satisfying
satisfying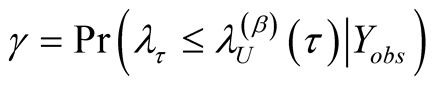 . From Equation (A.8)
and Equation (A.13)
. From Equation (A.8)
and Equation (A.13)
we have . This implies that
. This implies that
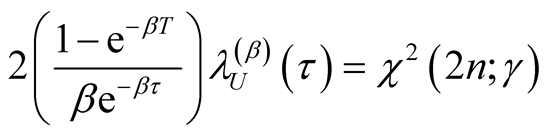 (A.14)
(A.14)
Making
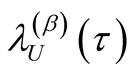 the subject from Equation (A.14) we arrive at
the subject from Equation (A.14) we arrive at
 (A.15)
(A.15)
Equation (A.15) is the exact formula in Equation (17).
The formula in Equation (18) can be obtained by similar arguments.


