ABSTRACT

Six categories of systematic designs derivable from the full 2^k factorial experiment by the interactions-main effects assignment are available for carrying out 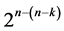factorial experiments sequentially run after the other such that main effects are protected against the linear/quadratic time trend and/or such that the number of factor level changes (i.e. cost) between the 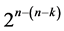runs is minimal. Three of these six categories are of resolution at least III and three are of resolution at least IV. 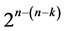The three categories of designs within each resolution are: 1) minimum cost designs, 2) minimum cost linear trend free designs and 3) minimum cost linear and quadratic trend free designs. This paper characterizes these six categories and documents their differences with regard to either time trend resistance of factor effects and/or the number of factor level changes. The paper introduces the last category of systematic 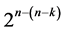designs (i.e. the sixth) for the purpose of extending the design resolution from III into IV and also for raising the level of protection of main effects from the linear time trend into the quadratic, where a catalog of minimum cost linear and quadratic trend free designs (of resolution at least IV) will be proposed. The paper provides for each 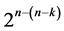design in any of the six categories: 1) the sequence of its runs in minimum number of factor level changes 2) the defining relation or its alias structure and 3) the k independent generators needed for sequencing the 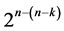runs by the generalized foldover scheme. A comparison among these six categories of designs reveals that when the polynomial degree of the time trend increases from linear into quadratic and/or when the design’s resolution increases from III to IV, the number of factor level changes between the 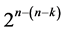runs increases. Also as the number of factors (i.e. n) increases, the design’s resolution decreases.

Keywords: Sequential Factorial Experimentation; Trend Resistant Run Orders; Generalized Fold-Over Scheme; Interactions-Main Effects Assignment; Cost of Factor Level Changes; Design Resolution

1. Introduction

Factorial experiments (confirmatory or exploratory) are experiments for studying the effect of several factors and their interactions on a particular outcome (i.e. response). Such experiments are either full or fractionated depending on whether three-factor and higher-order interactions are negligible or not. Fractional factorial experiments are more economical than full factorial experiments since they require less number of experimental runs. Experimentation cost can further be reduced if only two-level factors are studied in the experiment. Many full or fractionated experiments are carried out sequentially (not randomly) one run or one block at a time. This experimentation scheme suffers sometimes from some drawbacks, where main effects and/or two-factor interactions may be contaminated by the time trend which might be present in the successive responses, hence biasing factor effects. Therefore, it is essential to sequence runs of sequential factorial experiments such that: 1) factor effects are orthogonal to the time trend and to any uncontrollable factor aliased with this trend and/or such that 2) the number of factor level changes (i.e. cost) between successive runs is minimal. Cost can further be reduced if factors with expensive or difficult-to-vary-levels are minimally varied during successive experimentation.

For systematic complete 2ⁿ factorial experiments, there are four main algorithms for sequencing their 2ⁿ runs to overcome either of the above mentioned two problems. These algorithms are due to [1-4]. [5] has conducted a comparison among these algorithms and documented their differences according to three criteria: 1) which algorithm produces run orders in less number of factor level changes, 2) which algorithm produces run orders with more linear/quadratic time trend free main effects and 3) which run order of an algorithm can be generated by another algorithm using either the generalized foldover scheme or the interactions-main effects assignment.

In contrast and for systematic fractionated experiments, fewer algorithms exist for sequencing their 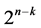runs to overcome the adverse effect of time trend on factor effects and/or to minimize the number of factor level changes between runs. [1] has extensively researched these two problems and summarized the literature and they also constructed efficient run orders for 2ⁿ and 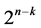factorial experiments using the interactions-main effects assignment. The work of [6] is another significant contribution, where they have proposed an algorithm utilizing the interactions-main effects assignment on the standard 2^k factorial experiment and constructed systematic 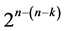designs (of resolutions at least III/at least IV) such that factor level changes between the 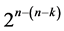runs are extreme (i.e. minimum or maximum) but without regard to factors’ resistance to the time trend and also without regard to how the runs can be sequenced in minimum number of factor level changes. Results [6] are based on three facts, the first and second proved by [1], the first stating that all k main effects and all interaction effects columns of the standard 2^k factorial experiment can be arranged in increasing number of level changes from 1 up to, while the second stating that any t-factor interaction (t ≥ 1) in the standard 2^k experiment is orthogonal to the time trend of degree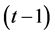. The third fact—proved by [6]—states that minimum/maximum cost 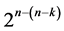designs (of resolutions at least III/at least IV) can be constructed from the standard 2^k experiment (with columns arranged in increasing number of level changes) by selecting sub-tables (i.e. 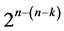designs)of n columns from the 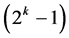effects columns and assigning them to new factors, where the number of factors ensuring design non-singularity and runs non-replication is for resolution at least III and is 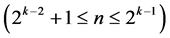for resolution at least IV. Section 2 provides illustration about these three facts.

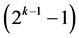For the purpose of achieving cost minimality (i.e. minimality of factor level changes between runs) as well as orthogonality of main effects to the linear time trend, [7] has extended minimum cost nonlinear trend free designs (of resolution at least III) due to [6] and constructed a catalog of minimum cost linear trend free designs 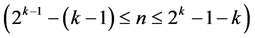of resolution at least III utilizing the interactions—main effects assignment on the standard full 2^k experiment, where all k main effects are excluded from the selection—assignment process due to their nonlinear time trend resistance. In addition and for the purpose of achieving cost minimality as well as linear trend resistance of main effects while ensuring main effects unaliased by non-negligible two-factor interactions, [8] has extended minimum cost nonlinear trend free 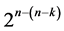designs (of resolution at least IV) due to [6] and constructed a catalog of 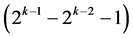minimum cost linear trend free 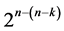designs of resolution at least IV utilizing the interactions-main effects assignment on the standard 2^k experiment, where all k main effects are excluded from the selection-assignment process for their nonlinear time trend resistance as well as excluding a total of interaction effects for violating resolution IV requirement. Section 2 provides illustration about factors’ linear trend resistance under either resolution III or IV.

Now in the case where a fractionated experiment is to be carried out sequentially run after run and the responses drift not only linearly with time but also quadratically, then it becomes necessary to sequence runs of this 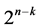experiment in minimum number of factor level changes such that main effects are orthogonal to the quadratic time trend as well as orthogonal to all non-negligible two-factor interactions. Therefore, this research intends to extend the two works of [6] on minimum cost (but nonlinear) trend free 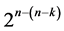designs (of resolution at least IV) which are economic and allow for the estimation of main effects un-aliased by non-negligible two-factor interactions and the work of [8] on minimum cost linear trend free 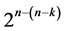designs (of resolution at least IV) which are economic and allow for the estimation of main effects unbiased by the linear (not the quadratic) time trend and unbiased by non-negligible two-factor interactions. This research extension results in the construction of a catalog of minimum cost linear and quadratic trend free 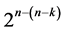designs (of resolution at least IV) by applying the interactions-main effects assignment on the standard 2^k experiment, where all k main effects and their 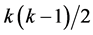two-factor interactions are excluded from the assignment for their non-quadratic time trend resistance as well excluding a total of 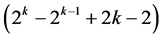three-factor and higher order interactions violating resolution IV requirement, hence leading to only a total of 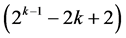three-factor and higher order interactions that are candidates for the assignment process. Section 3 provides illustration about these proposed systematic designs when k = 5. The following information will be provided for each proposed design: 1) the sequence of its 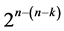runs in minimum number of factor level changes, 2) the defining relation or its alias structure and 3) the k independent generators needed for sequencing the 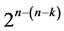runs by the generalized foldover scheme.

Linear and quadratic trend freeness of each proposed systematic 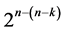design (i.e. orthogonality to the linear/quadratic time trend) besides orthogonality to non-negligible two-factor interactions can be established by the dot product (being zero) between entries (and entries squares) of the runs order vector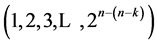

with each main effect column, where it is assumed that the 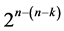runs are conducted sequentially run after the other at equally spaced time intervals from 1 up to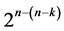. The Linear Time Count Statistic 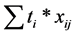and the Quadratic Time Count Statistic 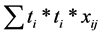of [9] are the two dot-product statistics often used for assessing factors’ time trend resistance in systematic factorial experiments, where x_ij (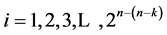and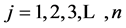) is the i^th entry of the j^th column of the design matrix representing a main effect or an interaction

(of +1’s and ‒1’s) and where the time index t_i is the i^th entry of the vector. Section 2 provides more clarification on these two Time Count Statistics. In addition, cost minimality (i.e. minimality of factor level changes) of the proposed 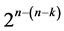designs is ensured by the selection and assignment of the first n interaction effects from the candidate interactions (arranged in increasing number of level changes), where any two proposed 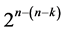designs in n and (n + 1) factors differ only in minimum number of factor level changes. It is worth to note here that quadratic trend freeness of each proposed 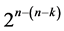design implies its linear trend freeness, a fact becomes clearer in Section 2.

For comprehensiveness purpose, this research will in addition characterize the six categories of systematic 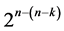designs that can be derived from the full 2^k factorial experiment by the interactions-main effects assignment for either protecting main effects against the linear/quadratic time trend and/or for minimizing the number factor level changes (i.e. cost) between runs. 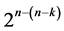Three of these six categories are of resolution at least III and they are: 1) minimum cost designs, 2) minimum cost linear trend free designs and 3) minimum cost linear and quadratic trend free designs. The other three categories are of resolution at least IV and they are: 4) minimum cost 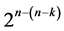designs, 5) minimum cost linear trend free designs and 6) minimum cost linear and quadratic trend free 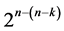designs, which is the category being proposed in this research. The first and fourth categories are due to [6] and the third and fifth categories are due to [7] and [8]. It is worth to note that the construction of these six categories of systematic 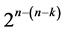designs differ by which main effect and interaction of the standard 2^k experiment are candidates for the interactions-main effects assignment, where for the first three categories of resolution at least III we note that:

1) the minimum cost 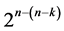designs in the first category incorporate all 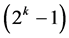effects of the 2^k experiment into assignment, 2) the minimum cost linear trend free 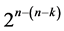designs in the second category exclude all k main effects of the 2^k experiment to secure linear trend resistance of all their n main effects, while 3) the minimum cost linear and quadratic trend free 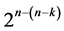designs in the third category exclude all k main effects as well as all 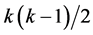two-factor interactions from assignment to secure linear and quadratic trend resistance of all their n main effects. On the other hand and for the three categories of resolution at least IV, we note that: 4) the minimum cost designs in the fourth category have only the following 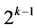candidate effects for assignment under resolution IV constraint: the two main effects A_k‒2 and A_k and the (2k ‒ 4) two-factor interactions A_k‒3A_k‒2, A_k‒4A_k‒2, ×××, A₂A_k‒2, A₁A_k‒2, A_k‒2A_k‒1, A_k‒1A_k, A_k‒3A_k, A_k‒4A_k, ×××, A₂A_k, A₁A_k as well as a total of 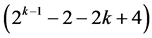three-factor and higher order interactions}, 5) the minimum cost linear trend free 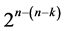designs in the fifth category exclude the two main effect {A_k‒2 and A_k} from the 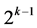candidate effects in the fourth category to secure both resolution IV and linear trend resistance of all their n main effects, while 6) the minimum cost linear and quadratic trend free designs in the six category exclude the two main effect {A_k‒2 and A_k} as well as the (2k ‒ 4) two-factor interactions {A_k‒3A_k‒2, A_k‒4A_k‒2, ×××, A₂A_k‒2, A₁A_k‒2, A_k‒2A_k‒1, A_k‒1A_k, A_k‒3A_k, A_k‒4A_k, ×××, A₂A_k, A₁A_k} from the 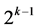candidate effects of the fourth category to secure both resolution IV and quadratic trend resistance of all n main effects. Sections 2 and 3 provide illustration for these 6 categories of systematic designs.

A comparison among these six categories of systematic designs will be conducted to see the effect of the two requirements of linear/quadratic time trend resistance and/or resolutions III/IV on the total number of factor level changes (i.e. cost). The rest of the paper is organized as follows: Section 2 characterizes the six categories of systematic 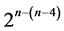designs that can be constructed from the standard 2⁴ factorial experiment by the interactions-main effects assignment and documents their differences. Section 3 proposes for the sixth category a catalog of three minimum cost linear and quadratic trend free 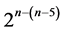designs of resolution at least IV (6 ≤ n ≤ 8) derived from the standard 2⁵ experiment by the interactions-main effects assignment. Section 4 generalizes results of Sections 2 and 3 and provides a characterization of the six categories of systematic designs that can be derived from the standard 2^k factorial experiment by the interactions-main effects assignment, where the sixth category is enriched by a catalog of minimum cost linear and quadratic trend free designs (of resolution at least IV). Section 5 provides a discussion and recommends optimal situations for the implementation of each category of these six categories of systematic designs.

2. Characterization of Six Categories of 16-Run Systematic 2^n‒(n‒4) Designs

This section characterizes the six categories of systematic 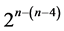designs that can be constructed from the complete 2⁴ factorial experiment by the interactions-main effects assignment for either the protection of main effects against the linear/quadratic time trend and/or for minimizing the number of factor level changes (i.e. cost) between the runs. To this end, the 2⁴ factorial experiment can be laid out as in Table 1, where main effects {A, B, C, D} and their interactions are in increasing number of level changes from 1 up to 15, as the third row from bottom of this table shows.

The 4 main effects in the 1^st, 3^rd, 7^th and 15^th columns are in their standard order. Linear and Quadratic Time Count Statistics in the last two rows of this table will be illustrated shortly. The order of the 15 = (2⁴ ‒ 1) factorial effects of this 2⁴ experiment at the top of Table 1, i.e.

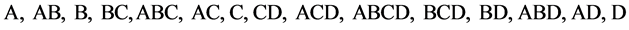(2.1)

can be obtained from the factorial effects order of the 2³ factorial experiment (in increasing number of level changes from 1 up to 7), i.e.

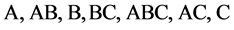(2.2)

by applying the reverse foldover algorithm of [10], where the first (2^4‒1 ‒ 1) = 7 effects in (2.1) are free from the 4^th factor and are exactly the same as those in effects order (2.2), while the last (2^4‒1 ‒ 1) = 7 interaction effects in (2.1) involve the 4^th factor and are obtained from the effects order (2.2) by adjoining the letter D to these effects in reverse order, then finally adding main effect D. In fact, this reverse algorithm can be implemented successively until the generation of the effects order of the complete 2^k experiment in increasing number of level changes (1 up to (2^k ‒ 1)) from the effects order of the full factorial experiment in increasing number of level changes from 1 up to.

For trend resistance of the standard 2⁴ experiment in Table 1, the 6 two-factor interactions {AB, AC, AD, BC, BD, CD} and the 4 three-factor interactions {ABC, ABD, ACD, BCD} as well as the 4-factor interaction ABCD they are linear, quadratic and cubic trend free, respectively, but the 4 main effects {A,B,C, D} are not even linear trend resistant. This fact can be verified by first changing zeros of Table 1 into −1’s to transform the 15 main effects and interactions into contrasts, then taking the dot product between each of these 15 contrasts and the entries(entries squares/cubes) of the run order vector (1, 2, 3, …, 16). Zero values for these two statistics (in the last two rows of Table 1) confirm that 3-factor interactions and 4-factor interactions are quadratic and cubic trend free, respectively. These two trend statistics show also that all 6 two-factor interactions are only linear trend free but not quadratic trend free, where their Linear Time Count is zero while their Quadratic Time Count is not zero. In addition, Table 1 confirms that quadratic trend freeness of an interaction effect implies also its linear trend freeness.

We next describe the six categories of 16-run systematic designs that can be constructed from the full 2⁴ experiment by the interactions-main effects assignment, where each design of each category has its own: 1) run sequence in minimum number of factor level changes, 2) defining relation (i.e. resolution) and 3) level in protection of main effects against the linear/quadratic time trend. For sequencing the 16 runs of each of these systematic 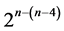designs in minimum number of factor level changes by the generalized foldover scheme, the 4 independent run generators in the 2^nd, 3^rd, 5^th and 9^th runs of each of these designs can be used for this purpose. Illustration of this runs sequencing process is given in category 3.

Category 1: minimum cost nonlinear trend free 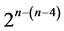designs of resolution at least III due to [6]. There are 8 = 2^4‒1 of these 16-run designs, where all n main effects of each design are orthogonally estimable as contrasts among the 16 runs under negligibility of all interaction effects and the time trend effect. Each of these 8 designs can be constructed from the standard 2⁴ experiment in Table 1 by the interactions-main effects assignment, where all 15 = (2⁴ ‒ 1) factorial effects are candidates for assignment. The largest of these designs (i.e. with the largest number of factors) is the 2^{15‒(15‒4)} design given by the 15 columns of Table 1 after renaming the15 effects columns by the new 15 main effects (A through O) according to the following interactions-main effects assignment:

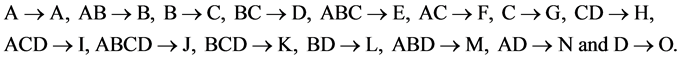
This is a minimum cost 2^{15‒(15‒4)} design (of resolution at least III) where its 16 runs are given by the 16 rows of Table 1 under the above effects column assignment, and where the total number of factor level changes (i.e. cost) is 120 calculated by summing the entries of the third row in the bottom of Table1 The (15 − 4) independent effects in the defining contrast of this 2^{15‒(15‒4)} design are: I = ABC = CDG = ADE = CEF = AFG = BEG = AHI = BIK = AJK = ALM = ANO. The other 7 minimum cost 16-run 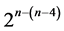designs can be obtained from this largest minimum cost 2^{15‒(15‒4)} design by successively deleting some of its last columns to preserve minimality of factor level changes, where deletion of the last column (i.e. factor O) produces a minimum cost 2^{14‒(14‒4)} design and deletion of the last two columns (i.e. factors N and O) produces a minimum cost 2^{13‒(13‒4)} design, until the deletion of the last 7 columns which produces the smallest minimum cost 2^8‒(8‒4) design, where the 4 independent effects of its defining relation are I = ABC = AFG = BDF = ABCDEFG and where this design’s 16 runs are sequenced as follows:

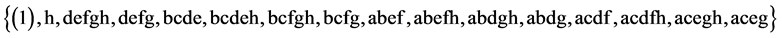(2.3)

with total number of factor level changes 36 = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8). The 4 independent run generators needed for generating this run sequence in (2.3) by the generalized foldover scheme are {h, defgh, bcde, abef}, where for illustration see the systematic 2^5‒(5‒4) design in the third category.

Category 2: minimum cost linear trend free 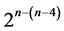designs of resolution at least III 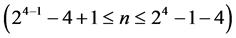due to [7]. There are 7 of these 16-run designs, where main effects are orthogonally estimable as contrasts among the 16 runs un-aliased by the linear time trend under negligibility of all interaction effects. Each of these seven 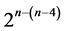designs can be constructed from the standard 2⁴ experiment in Table 1 by the interactions-main effects assignment after excluding all 4 main effects columns {A, B, C, D} for their nonlinear trend resistance. The remaining eleven interaction columns in increasing number of level changes constitute under the interactions-main effects assignment:

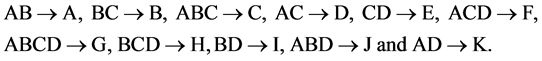
the largest minimum cost linear trend free 2^{11‒(11‒4)} design, where its 16 runs are the16 rows of Table 1 under this assignment and where the total number of factor level changes is 94. The 7 = (11 ‒ 4) independent effects in the defining contrast of this 2^{11‒(11‒4)} design are: I = ABD = BEI = CEJ = DEK = AEG = AFH = BGK. The other 6 minimum cost linear trend free 16-run 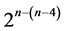designs can be constructed from this largest minimum cost linear trend free 2^{11‒(11‒4)} design by successively deleting some of its last columns to preserve minimality of factor level changes, until the deletion of its last 6 columns which produces the smallest minimum cost linear trend free 2^5‒(5‒4) design with defining relation I = ABD and runs sequence:

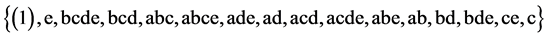(2.4)

where the total number of factor level changes is 25 = (2 + 4 + 5 + 6 + 8).

Category 3: Minimum cost linear and quadratic trend free 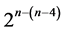designs of resolution at least III. There is only one 16-run systematic design in n = 5 factors, where all 5 main effects are orthogonally estimable as contrasts among the 16 runs un-aliased by the linear and quadratic time trend under negligibility of all interaction effects. This 2^5‒(5‒4) design can be constructed from the standard 2⁴ experiment in Table 1 by the interactions-main effects assignment after deleting all 4 main effects columns {A, B, C, D} and all 6 two-factor interactions {AB, AC, AD, BC, BD, CD} for their non-quadratic trend resistance. The remaining five interaction columns of Table 1 produce under the assignment:

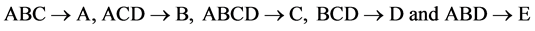
A minimum cost linear and quadratic trend free 2^5‒(5‒4) design, where its 16 runs are sequenced as:

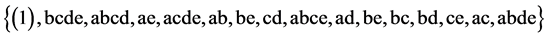(2.5)

and where its defining contrast is I = ABCDE and its total number of factor level changes is 48 = (5 + 9 + 10 + 11 + 13). The 2^nd, 3^rd, 5^th and 9^th runs of this design {bcde = g₁, abcd = g₂, acde = g₃, abce = g₄} are the 4 independent run generators needed for the generalized foldover scheme to generate the same 16-run sequence in (2.5) as follows:

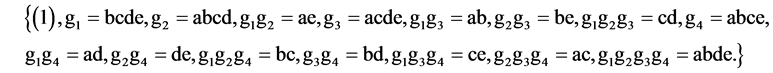
Of course, there are (16)! = 20922789890000 possible run orders among the 16 runs of this 2^5‒(5‒4) design but not all of these run orders render main effects linear and quadratic trend free. In addition, other systematic 2^5‒(5‒4) designs with total number of factor level changes (i.e. cost) less than 48 can be constructed from the standard 2⁴ experiment in Table 1 by selecting and assigning other 5 columns but neither cost minimality nor quadratic trend resistance will be preserved. Also, constructing by the interactions-main effects assignment systematic 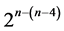designs in less than 5 factors leads either to 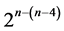designs with replicated runs or to complete 2⁴ factorial designs, while constructing systematic 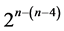designs in more than 5 factors sacrifices quadratic trend resistance and/or leads to designs with replicated runs. Therefore, category 3 contains only one minimum cost linear and quadratic trend free 16-run 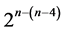design, namely the design in (2.5).

Category 4: minimum cost nonlinear trend free 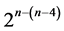designs of resolution at least IV 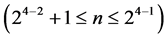due to [6]. There are 4 of these16-run 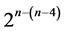designs, where main effects are estimable as contrasts among its 16 runs un-aliased by non-negligible two-factor interactions if time trend is negligible. Each of these four 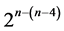designs can be constructed from the standard 2⁴ experiment by the interactions-main effects assignment after deleting the 7 factorial effects columns {A, AC, C, ABCD, BCD, BD, ABD} for violating resolution IV requirement. The remaining 8 effects columns {AB, B, BC, ABC, CD, ACD, AD, D} constitute under the assignment:

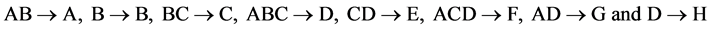
the largest minimum cost 2^8‒(8‒4) design of resolution IV, where the 4 independent effects of its defining relation are I = ABCD = ABEF = ABGH = ACEG and where its 16 runs are sequenced as:

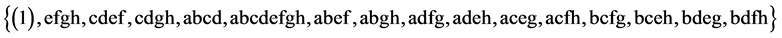(2.6)

The 2^nd, 3^rd, 5^th and 9^th runs {efgh, cdef, abcd, adfg} of this design are the 4 independent generators that generate this runs sequence in (2.6) by the generalized foldover scheme, where cost is 60= (2 + 3 + 4 + 5 + 8 + 9 + 14 + 15). The other 3 minimum cost designs can be obtained from this largest minimum cost 2^8‒(8‒4) design by successively deleting some of its last columns to preserve minimality of factor level changes, until the deletion of the last 3 columns which produces the smallest minimum cost 2^5‒(5‒4) design with defining relation I = ABCD, where its 16 runs are sequenced as:

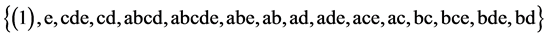(2.7)

The 2^nd, 3^rd, 5^th and 9^th runs {e, cde, abcd, ad} are the 4 independent generators needed for generating this 16-run sequence in (2.7) by the generalized foldover scheme, where the total number of factor level changes is 22= (2 + 3 + 4 + 5 + 8).

Category 5: minimum cost linear trend free 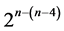designs of resolution at least IV 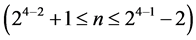due to [8]. There are 2 of these 16-run systematic 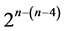designs, where main effects are estimable as orthogonal contrasts un-aliased by either the non-negligible two-factor interactions or the linear time trend. Each of these two 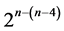designs can be constructed from the 8 = 2^4‒1 candidate effects columns {AB, B, BC, ABC, CD, ACD, AD, D}of the 2⁴ factorial experiment by the interactions-main effects assignment after deleting the two main effects {B, D} for their nonlinear time trend resistance. The remaining 6 interaction columns constitute under the assignment:

the largest minimum cost linear trend free 2^6‒(6‒4) design, where its defining relation is I = ABDF = ACEF = BCDE and where its 16 runs are sequenced as:

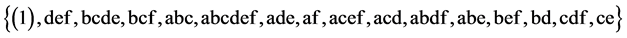
The 2^nd, 3^rd, 5^th and 9^th runs {def, bcde, abc, acef} are its 4 independent generators, where the total number of factor level changes is 42= (2 + 4 + 5 + 8 + 9 + 14). The other minimum cost linear trend free 2^5‒(5‒4) design is constructed from this largest 2^6‒(6‒4) design by deleting its last column to preserve minimality of factor level changes. The resulting systematic 2^5‒(5‒4) design has the defining relation I = BCDE and its 16 runs are sequenced as:

(2.8)

where the total number of factor level changes is 28 = (2 + 4 + 5 + 8 + 9).

Category 6: Minimum cost linear and quadratic trend free designs (of resolution at least IV). These 16-run designs (if exist) can be constructed from the 8 = 2^4‒1 candidate effects columns of the 2⁴ factorial experiment {AB, B, BC, ABC, CD, ACD, AD, D) under resolution IV by the interactions-main effects assignment after deleting the two main effects {B, D} and the four two-factor interactions {AB, BC, CD, AD} for their nonquadratic time trend resistance. The remaining two interaction columns {ABC, ACD} produce under the assignment:

{ABC→A and ACD→B} a degenerate minimum cost linear trend free 2-factor design of resolution at least IV with replicated runs. Section 3 produces a catalog of three 32-run non-degenerate minimum cost linear and quadratic trend free 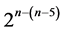designs of resolution at least IV (6 ≤ n ≤ 8).

We now compare these six categories of 16-run systematic 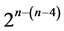designs and notice that raising up the design’s resolution from III into IV increases the total number of factor level changes (i.e. cost). We also notice from the comparison among the three systematic 2^5‒(5‒4) designs in (2.4), (2.5) and (2.8) that lifting up the level of protection of main effects from the linear time trend into the quadratic increases the design’s cost. In addition, as the number of factors (i.e. n) increases, the design’s resolution decreases.

3. A Catalog of Minimum Cost Linear and Quadratic Trend Free 2^n‒(n‒5) Designs of Resolution at Least IV (6≤ n ≤ 8)

There are six categories of 32-run systematic 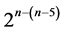designs that can be constructed from the full 2⁵ factorial experiment by the interactions-main effects assignment. This section concentrates on the sixth category and constructs three 32-run minimum cost linear and quadratic trend free 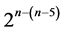designs of resolution at least IV (6 ≤ n ≤ 8). To this end, the full 2⁵ factorial experiment can be laid out such that main effects and interaction columns are in increasing number of level changes (from 1 up to 31) if these columns are arranged as follows:

(3.1)

Main effects {A, B, C, D, E} in the 1^st, 3^rd, 7^th, 15^th and 31^st columns of this 2⁵ experiment are in their standard order with 1,3,7,15 and 31 level changes, respectively. This effects order in (3.1) can also be obtained—as illustrated in (2.1) and (2.2) of Section 2—from the effects order of the 2⁴ factorial experiment by the reverse foldover algorithm.

We now identify the 16 = 2^5‒1 factorial effects of the 2⁵ experiment that are candidates for assignment under resolution IV. These 16 candidate effects are:{BC, ABC, AC, C, CD, ACD, ABCD, BCD, DE, ADE, ABDE, BDE, BE, ABE, AE, E}, which include the 2 main effects {C, E} and the 6 two-factor interactions {BC, AC, CD, DE, BE and AE} while the remaining 8 effects are 3-factor and higher order interactions. These 16 candidate effects columns (in increasing number of level changes) produce under the assignment:

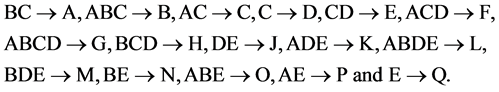
the largest minimum cost 2^{16‒(16‒5)} design (of resolution at least IV). This 2^{16‒(16‒5)} design is not time trend free if time trend is non-negligible, since some effects in this assignment are main effects of the underlying 2⁵ experiment which are nonlinear trend free. Therefore, to ensure linear and quadratic trend resistance of main effects while maintaining resolution IV, we delete the 2 main effects columns {C and E} and the 6 two-factor interaction columns {BC, AC, CD, DE, BE and AE} from this largest minimum cost 2^{16‒(16‒5)} design. The resulting systematic 2^8‒(8‒5) design is given in Table 2 under the assignment:

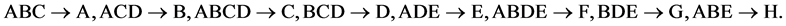
This is a minimum cost linear and quadratic trend free 2^8‒(8‒5) design (of resolution at least IV) and its defining relation is I = ABEH = ACFH = ADGH = BCEF = BDEG = CDFG = ABCDEFGH, where its runs sequence is as follows:

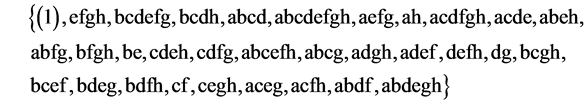
The total number of factor level changes is 118 = (5 + 9 + 10 + 11 + 17 + 18 + 19 + 29) and the 5 independent generators needed for the generalized foldover scheme are the 2^nd, 3^rd, 5^th, 9^th and 17^th runs, namely {efgh, bcdefg, abcd, acdfgh, abcefh}. All eight main effects of this 2^8‒(8‒5) design are estimable un-aliased by either the non-negligible two-factor interactions or the quadratic time trend effect.

The other 2 minimum cost linear and quadratic trend free designs of resolution at least IV (6 ≤ n < 8) can be obtained from this largest minimum cost linear and quadratic trend free 2^8‒(8‒5) design by successively deleting some of its last columns to preserve minimality of factor level changes, until the deletion of its last 2 columns which produces the smallest minimum cost linear and quadratic trend free 2^6‒(6‒5) design (of resolution at least IV) with defining relation I = BCEF and with run structure:

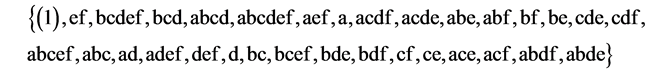
The 2^nd, 3^rd, 5^th, 9^th and 17^th runs of this smallest 2^6‒(6‒5) design {ef, bcdef, abcd, acdf, abcef} are the 5 independent generators needed for sequencing its 32 runs in minimum number of factor level changes by the generalized foldover scheme with total cost 70 = (5 + 9 + 10 + 11 + 17 + 18).

4. Characterization of Six Systematic 2^n‒(n‒k) Designs

This section generalizes results of Sections 2 and 3 and characterizes the six categories of systematic 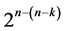designs that can be constructed from the standard 2^k factorial experiment by the interactions-main effects assignment and also enriches the sixth category with a catalog of minimum cost linear and quadratic trend free

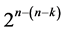designs of resolution at least IV. The 2^nd, 3^rd, 5^th, 9^th, 17^th, ×××, 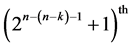runs of each of these

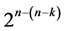designs in the 6 categories are the k independent run generators needed for sequencing their runs in minimum number of factor level changes by the generalized foldover scheme. The starting stepin this characterization is to lay out the 2^k factorial experiment such that main effect and interaction columns are in increasing number of level changes from 1 up to (2^k ‒ 1), where we code these (2^k ‒ 1) effect columns by C_i with increasing index. Index i of effect C_i represents also the number of level changes in this effect column. That is, effect column C_i has i number level changes. Next is the characterization of the 6 categories of systematic 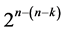designs:

Category (1): contains a catalog of 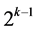minimum cost 2^n-(n-k) designs of resolution at least III, where all 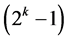effects columns C_i 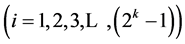of the standard 2^k experiment are candidates for assignment. The largest of these 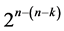designs incorporates all effects columns into assignment, leading to a minimum cost 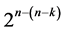design (of resolution at least III) in 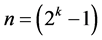factors with total number of factor level changes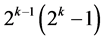, where its 2^k runs are given by all 2^k rows of the 2^k factorial experiment under this assignment. This largest minimum cost design is economic with minimum number of factor level changes but its n main effects are not time trend resistant if this trend is non-negligible. 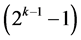The remaining systematic designs can be constructed from this largest minimum cost 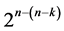design by deleting some of its last columns to preserve minimality of factor level changes, until the deletion of its last 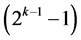effects columns which produces the smallest minimum cost 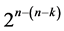design (of resolution at least III) in 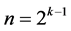factors with total number of factor level changes =.

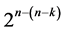Category (2): contains a catalog of minimum cost linear trend free designs of resolution at least III, where all k main effects of the 2^k experiment are excluded from the assignment to secure linear trend resistance for all main effects. The largest of these 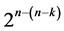designs incorporates all 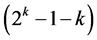interaction effects columns into the assignment, which leads to a minimum cost linear trend free 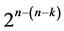design (of resolution at least III) in factors with total number of factor level changes =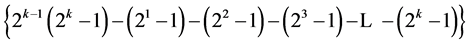. The 2^k runs of this 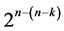design are the 2^k rows of the 2^k factorial experiment under all its 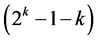interaction columns. The remaining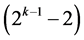

systematic 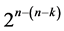designs can be generated from this largest minimum cost linear trend free 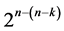design by deleting some of its last columns, until the deletion of the last 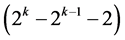effects columns which produces the smallest minimum cost 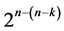design (of resolution at least III) in 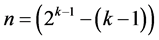factors.

Category (3): contains a catalog of 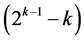minimum cost linear and quadratic trend free 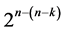designs of resolution at least III 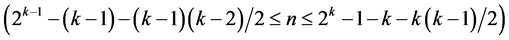in increasing number of factors from 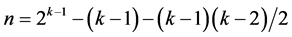up to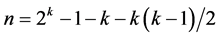. All k main effects as well as all two-factor interactions of the 2^k experiment are excluded from assignment to secure linear and quadratic trend resistance of all main effects. 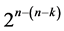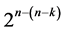The largest of these designs incorporates all selected and assigned three-factor and higher order interaction columns, which leads to a minimum cost linear and quadratic trend free design (of resolution at least III) in

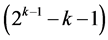factors. The 2^k runs of this design are the 2^k rows of the 2^k experiment under all selected and assigned three-factor and higher order interaction columns. The remaining systematic 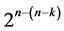designs can be generated from this largest minimum cost linear and quadratic trend free 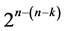design by deleting some of its last columns, until the deletion of its last effects columns which produces the smallest minimum cost linear and quadratic trend free 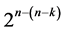design (of resolution at least III) in 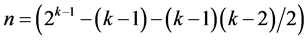factors.

Category (4): contains a catalog of 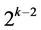minimum cost designs of resolution at least IV 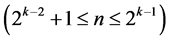, where only 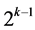effects of the 2^k factorial experiment are candidates for assignment under resolution IV requirement. These 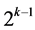effects are in increasing number of level changes and include: the two main effects A_k‒2 and A_k and the (2k ‒ 4) two-factor interactions A_k‒3A_k‒2, A_k‒4A_k‒2, ×××, A₂A_k‒2, A₁A_k‒2, A_k‒2A_k‒1, A_k‒1A_k, A_k‒3A_k, A_k‒4A_k, ×××, A₂A_k, A₁A_k as well as a total of 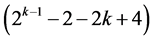three factor and higher order interactions. These candidate effects can be grouped—by the above columns coding 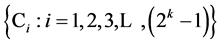—into three sets of successive effects as follows:

Group One: contains the 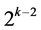effects columns C_i, for, , , ×××, , , , ×××,.

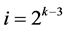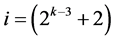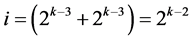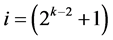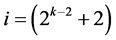Group Two: contains the effects columns C_i, for, , ×××,.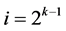

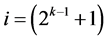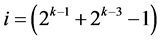Group Three: contains the effects columns C_i,, for, , ×××, ,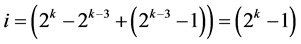. (4.1)

Group One consists of 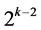successive effects (in increasing number of level changes from 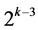up to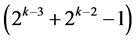), where it starts with the two-factor interaction A_k‒3A_k‒2 at colum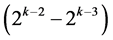n in 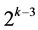level changes and ends with the two-factor interaction A_k‒2A_k‒1 at column 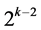in level changes.

This group contains the main effect A_k‒2 at column between the 2 two-factor interactions A₁A_k‒2 at column and A_k‒2A_k‒1 at column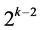. This group contains also the (k ‒ 2) two-factor interactions

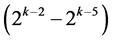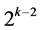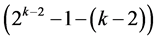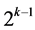at columns, , , ×××, , , respectively. The remaining effects of this group are three-factor and higher order interactions. Group Two contains successive effects (in increasing number of level changes from up to 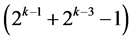without any intervening main effects, where it starts with the only two-factor interaction A_k‒1A_k at colum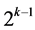n in 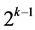level changes, while the other 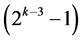effects of this group are three-factor and higher order interactions. Finally, Group Three consists of 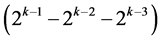successive interaction effects (in increasing number of level changes from up to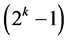), where it starts with the two-factor interaction A_k‒3A_k at column in 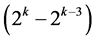level changes and ends with the only main effect in this group A_k at column 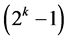with 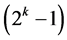level changes. Group Three contains also the (k ‒ 3) two-factor interactions 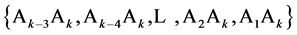at columns

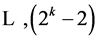, respectively. The remaining 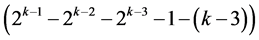effects of Group Three are 3-factor and higher order interactions.

For illustration of the effects grouping of the 2^k experiment in (4.1) under resolution IV, we take k = 5 and refer to the effects order (3.1) of the 2⁵ experiment in increasing number of level changes from 1 up to 31. These 31 effects columns are coded as, where effect column C₉ in (3.1) represents the threefactor interaction ACD in 9 level changes. The 16 = 2^5‒1 factorial effects candidates for interactions-main effects assignment under resolution IV can be grouped—according to (4.1)—into three groups of successive factorial effects as follows:

Group One: contains the 2^5‒2 = 8 effects columns C_i 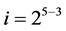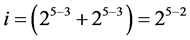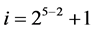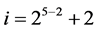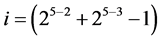{, , , ×××, , , , ×××, } in increasing number of level changes from 2^5‒3 into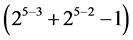. They are the 8 effects {BC, ABC, AC,C, CD, ACD, ABCD, BCD} in (3.1) in level changes from 2^5‒3 up to.

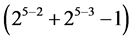Group Two: contains the 2^5‒3 = 4 effects columns C_i {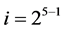, , 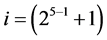×××, 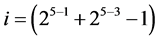} in increasing number of level changes (from 2^5‒1 into). They are the 4 interaction effects {DE, ADE, ABDE, BDE} in (3.1) in level changes from 2^5‒1 up to.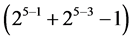

Group Three: contains the 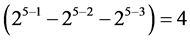effects columns C_i {, , 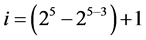×××, 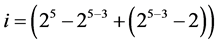, 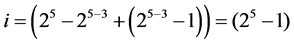} in increasing number of level changes from (2⁵–2^5‒3) into (2⁵‒1). They are the 4 effects {BE, ABE, AE, E} in (3.1) in level changes from (2⁵–2^5‒3) up to (2⁵‒1).  (4.2)

Collecting all 2^5‒1 = (8 + 4 + 4) candidate effects of the 2⁵ experiment under resolution IV in (4.2) gives the 16-element effects set {BC, ABC, AC,C, CD, ACD, ABCD, BCD, DE, ADE, ABDE, BDE, BE, ABE, AE, E}, which produces by the interactions-main effects assignment the largest minimum cost 2^{16‒(16‒5)} design (of resolution at least IV) in n = 2^5‒1 factors with total number of factor level changes 248 = 2^5‒2(2⁵ ‒ 1). All 16 main effects of this 2^{16‒(16‒5)} design are estimable un-aliased by non-negligible two-factor interactions but are not free from aliasing with the time trend, if this trend is non-negligible. The remaining (2^5‒2 ‒ 1) minimum cost 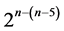designs (of resolution at least IV) can be generated from this largest minimum cost 2^{16‒(16‒5)} design by deleting some of its last columns, until the deletion of its last 7 effects columns which produces the smallest minimum cost 2^9‒(9‒5) design (of resolution at least IV) in n = (2^5‒2 + 1) factors. Section 2 has more illustration for 16-run minimum cost 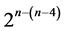designs (of resolution at least IV).

Therefore and based on the effects grouping in (4.1), the largest minimum cost 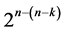design (of resolution at least IV) in the fourth category incorporates all 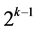candidate effects columns of the 2^k experiment in the three groups. The 2^k runs of this 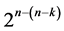design are the 2^k rows of the 2^k experiment under all these candidate effects columns with total number of factor level changes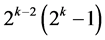. All n main effects of this design are estimable un-aliased by non-negligible two-factor interactions but aliased with the time trend, if this trend is non-negligible. There maining systematic 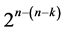designs in this category can be generated fromthis largest minimum cost linear trend free 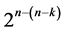design (of resolution at least IV) by deleting some of its last columns, until the deletion of the last 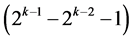effects columns which produces the smallest minimum cost design (of resolution at least IV) in 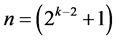factors.

Category (5): contains a catalog of minimum cost linear trend free 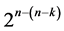designs of resolution at least IV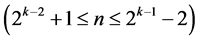, where the two main effect {A_k‒2,A_k} in the 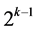candidate effects of the fourth category are excluded from assignment to secure both resolution IV and main effects linear trend resistance. The largest of these designs incorporates all interaction effects columns into the assignment, leading to a minimum cost linear trend free 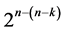design (of resolution at least IV) in

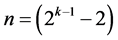factors with total number of level changes =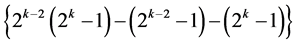. The 2^k runs of this 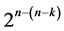design are the 2^k rows of the 2^k experiment under these 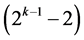selected and assigned interactions. All n main effects of this 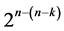design are estimable un-aliased by non-negligible two-factor interactions and orthogonal to the linear time trend. 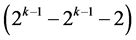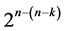The remaining systematic designs in this category can be generated from this largest minimum cost linear trend free design by deleting some of its last columns, until the deletion of its last effects columns which produces the smallest minimum cost linear trend free 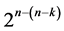design (of resolution at least IV) in 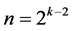factors with total number of factor level changes =.

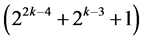Category (6): contains a catalog of minimum cost linear and quadratic trend free 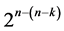designs of resolution at least IV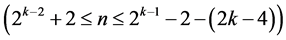, where the two main effect {A_k‒2, A_k} as well as the (2k ‒ 4) two-factor interactions {A_k‒3A_k‒2, A_k‒4A_k‒2, ×××, A₂A_k‒2, A₁A_k‒2, A_k‒2A_k‒1, A_k‒1A_k, A_k‒3A_k, A_k‒4A_k, ×××, A₂A_k, A₁A_k} in the 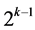candidate effects of the fourth category are excluded to secure both resolution IV and main effects quadratic trend resistance. Therefore, a total of 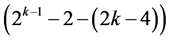three-factor and higher order interactions are candidates for assignment. The largest design in this category incorporates all these candidate interactions into the assignment, leading to a minimum cost linear and quadratic trend free 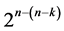design(of resolution at least IV) in 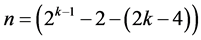factors with total number of factor level changes = {2^k‒2(2^k ‒ 1) ‒ (2^k‒2 ‒ 1) ‒ (2^k ‒ 1) ‒ (2^k‒2 ‒ 2^k‒3) ‒ (2^k‒2 ‒ 2^k–4) – (2^k–2 ‒ 2^k–5) ‒ ××× ‒ (2^k–2 – 2) ‒ 2^k–2 – (2^k – 2^k–3) ‒ (2^k ‒ 2^k–4) ‒ (2^k ‒ 2^k–5) ‒ ××× ‒ (2^k ‒ 2)}. The 2^k runs of this design are the 2^k rows of the 2^k experiment under these selected and assigned three-factor and higher order interactions. All n main effects of this largest 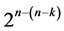design are estimable un-aliased by nonnegligible two-factor interactions and are orthogonal to the linear and quadratic time trend. The remaining systematic 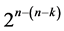designs of this category can be generated from this largest 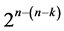design by deleting some of its last columns.

5. Discussion and Recommendations

Literature is abundant with regular and non-regular fractional factorial designs for carrying out fractional factorial experiments randomly or systematically. However, literature lacks fractional factorial designs that can be carried out systematically run after run in minimum number of factor level changes such that main effects are robust against the quadratic time trend effect as well as free from aliasing with non-negligible two-factor interactions. With the introduction of the proposed minimum cost linear and quadratic trend free 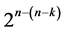designs (of resolution at least IV) in the sixth category, there exists now six categories of systematic 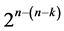designs derivable from the 2^k factorial experiment by the interactions-main effects assignment. This research has characterized these 6 categories and documented their differences. Therefore, if a fractionated 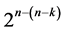experiment is to be carried out sequentially run after run, the following argument can be entertained which leads to recommendations about optimality of the implementation of each category of these designs:

a) if two-factor interactions are negligible and resolution at least III is adequate, then the minimum cost 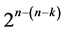designs in the first category due to [6] are preferable if time trend effect is negligible, since they are the most economical and their number of factor level changes (i.e. cost) is the minimal. Whereas if time trend is non-negligible of linear form, then the minimum cost linear trend free 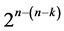designs in the second category due to [7] are more appropriate, although their total number of factor level changes (i.e. cost) is higher than 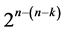designs of the first category. In contrast, if time trend is non-negligible of quadratic form, then the minimum cost linear and quadratic trend free designs(of resolution at least III) in the third category are more appropriate although their total number of factor level changes (i.e. cost) is larger the cost of the 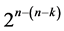designs in the first and second categories.

b) if two-factor interactions are non-negligible and resolution at least IV is required, then the minimum cost 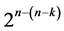designs in the fourth category due to [6] are preferable if time trend effect is negligible. Whereas, if time trend is non-negligible of linear form, then minimum cost linear trend free 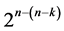designs in the fifth category due to [8] are more appropriate although their total number of factor level changes (i.e. cost) is higher than the cost of 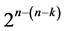designs of [6] in the fourth category. In contrast, if time trend is non-negligible of quadratic form, then the proposed minimum cost linear and quadratic trend free 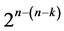designs in the sixth category are the most appropriate although their total number of factor level changes is the largest among all 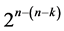designs in the six categories.

[1] REFERENCES

[2] C. S. Cheng and M. Jacroux, “The Construction of Trend-Free Run Orders of Two-Level Factorial Designs,” Journal of the American Statistical Association, Vol. 83, No. 404, 1988, pp. 1152-1158. http://dx.doi.org/10.1080/01621459.1988.10478713

[3] D. C. Coster and C. S. Cheng, “Minimum Cost Trend-Free Run Orders of Fractional Factorial Designs,” Annals of Statistics, Vol. 16, No. 3, 1988, pp. 1188-1205. http://dx.doi.org/10.1214/aos/1176350955

[4] X. Cui and P. W. John, “Time Trend Free Run Orders with Minimum Level Changes,” Communications in Statistics-Theory and Methods, Vol. 27, No. 1, 1998, pp. 55-68. http://dx.doi.org/10.1080/03610929808832650

[5] A. A. Correa, P. Grima and Tort-Martorell, “Experimentation Order with Good Properties for 2^k Factorial Designs,” Journal of Applied Statistics, Vol. 36, No. 7, 2009, pp. 743-754. http://dx.doi.org/10.1080/02664760802499337

[6] H. M. Hilow, “Comparison among Run Order Algorithms for Sequential Factorial Experiments,” Journal of Computational Statistics and Data Analysis, Vol. 58, 2013, pp. 397-406. http://dx.doi.org/10.1016/j.csda.2012.09.013

[7] C. S. Cheng, R. J. Martin and B. Tang, “Two-Level Factorial Designs with Extreme Number of Level Changes,” The Annals of Statistics, Vol. 26, No. 4, 1998, pp. 1522-1539. http://dx.doi.org/10.1214/aos/1024691252

[8] H. M. Hilow, “Minimum Cost Linear Trend Free Fractional Factorial Designs,” Journal of Statistical Theory and Practice, Vol. 6, No. 3, 2012, pp. 580-589. http://dx.doi.org/10.1080/15598608.2012.698209

[9] H. M. Hilow, “Minimum Cost Linear Trend Free 2^n-(n-k) Designs of Resolution IV,” Accepted for Publication in Communications in Statistics—Theory and Methods, 2013.

[10]  N. R. Draper and D. M. Stoneman, “Factor Level Changes and Linear Trends in Eight-Run Two-Level Factorial Designs,” Technometrics, Vol. 10, No. 2, 1968, pp. 301-311. http://dx.doi.org/10.1080/00401706.1968.10490562

[11]  C. S. Cheng and D. M. Steinburg, “Trend Robust Two-Level Factorial Designs,” Biometrika, Vol. 78, No. 2, 1991, pp. 325- 336. http://dx.doi.org/10.1093/biomet/78.2.325