Open Journal of Statistics
Vol.3 No.4(2013), Article ID:35942,5 pages DOI:10.4236/ojs.2013.34032
A New Estimator Using Auxiliary Information in Stratified Adaptive Cluster Sampling
Department of Mathematics, Faculty of Science, Mahasarakham University, Maha Sarakham, Thailand
Email: *j3832024@hotmail.com
Copyright © 2013 Nipaporn Chutiman et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 2, 2013; revised July 2, 2013; accepted July 9, 2013
Keywords: Stratified adaptive cluster sampling; auxiliary variable; ratio estimator; product estimator
ABSTRACT
In this paper, we study the estimators of the population mean in stratified adaptive cluster sampling by using the information of the auxiliary variable. Simulations showed that if the variable of interest (y) and the auxiliary variables (x,z) have high positive correlation then the estimate of the mean square error of the ratio estimators is less than the estimate of the mean square error of the product estimator. The estimators which use only one auxiliary variable were better than the estimators which use two auxiliary variables.
1. Introduction
Adaptive cluster sampling, proposed by Thompson [1], is an efficient method for sampling rare and hidden clustered populations. In adaptive cluster sampling, an initial sample of units is selected by simple random sampling. If the value of the variable of interest from a sampled unit satisfies a pre-specified condition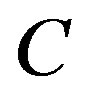 , that is
, that is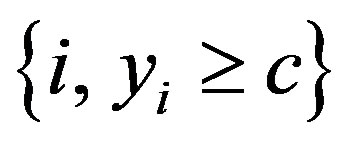 , then the unit’s neighborhood will also be added to the sample. If any other units that are “adaptively” added also satisfy the condition
, then the unit’s neighborhood will also be added to the sample. If any other units that are “adaptively” added also satisfy the condition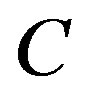 , then their neighborhoods are also added to the sample. This process is continued until no more units that satisfy the condition are found. The set of all units selected and all neighboring units that satisfy the condition is called a network. The adaptive sample units, which do not satisfy the condition are called edge units. A network and its associated edge units are called a cluster. If a unit is selected in the initial sample and does not satisfy the condition
, then their neighborhoods are also added to the sample. This process is continued until no more units that satisfy the condition are found. The set of all units selected and all neighboring units that satisfy the condition is called a network. The adaptive sample units, which do not satisfy the condition are called edge units. A network and its associated edge units are called a cluster. If a unit is selected in the initial sample and does not satisfy the condition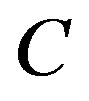 , then there is only one unit in the network. A neighborhood must be defined such that if unit
, then there is only one unit in the network. A neighborhood must be defined such that if unit 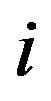 is in the neighborhood of unit
is in the neighborhood of unit  then unit
then unit  is in the neighborhood of unit
is in the neighborhood of unit . In this paper, a neighborhood of a unit is defined as the four spatially adjacent units, that is to the left, right, top and bottom of that unit as shown in Figure 1.
. In this paper, a neighborhood of a unit is defined as the four spatially adjacent units, that is to the left, right, top and bottom of that unit as shown in Figure 1.
Figure 1 illustrates the example of a network. The unit with a star is the initial unit selected. The condition to adaptively added units is a value greater than or equal to 1. Units that are to the left, right, top, and bottom of one another making up a neighborhood. The units in the gray shading form a single network. The units in bold numbers are edge units of the network. The network and its edge units make up a cluster.
Adaptive cluster sampling are applied in stratified random sampling. In adaptive cluster sampling, an initial stratified sample is selected from a population, and whenever the variable of interest for any unit is observed to satisfy the condition, the neighborhood of that unit is added in the sample. Sometimes other variables are related to the variable of interest y. We can obtain additional information for estimating the population mean. The use of an auxiliary variable is a common method to improve the precision of estimates of a population mean. In this paper, we will study the estimator of population mean in stratified adaptive cluster sampling using an auxiliary

Figure 1. The example of network where a unit neighborhood is defined as four spatially adjacent units.
variable. Some comparisons are made using a simulation.
2. Stratified Adaptive Cluster Sampling
For stratified adaptive cluster sampling, the population consists of 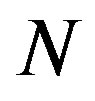 units partitioned into
units partitioned into  strata based on prior information about units that are similar, and it is assumed that the population ignores crossover between strata. The population in each stratum consists of
strata based on prior information about units that are similar, and it is assumed that the population ignores crossover between strata. The population in each stratum consists of 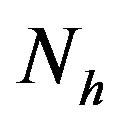 units
units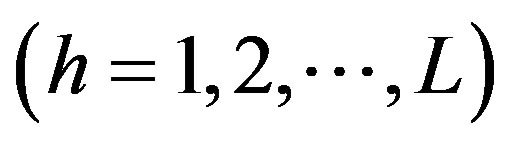 . The population mean of the variable of interest in stratum h is
. The population mean of the variable of interest in stratum h is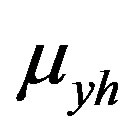 . An initial sample of unit size
. An initial sample of unit size  is selected by simple random sampling without replacement and for those units selected that satisfy the condition. Then the unit’s neighborhood is added to the sample.
is selected by simple random sampling without replacement and for those units selected that satisfy the condition. Then the unit’s neighborhood is added to the sample.
Define

is the average of the y-values of the network to which  belongs.
belongs. 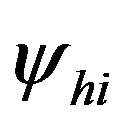 is the network that include unit i in stratum h and
is the network that include unit i in stratum h and 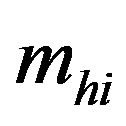 is the size of network that include unit
is the size of network that include unit  in stratum
in stratum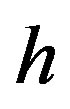 . The estimator of the population mean based on Hansen-Hurwitz estimator (Thompson and Seber [2]) is
. The estimator of the population mean based on Hansen-Hurwitz estimator (Thompson and Seber [2]) is
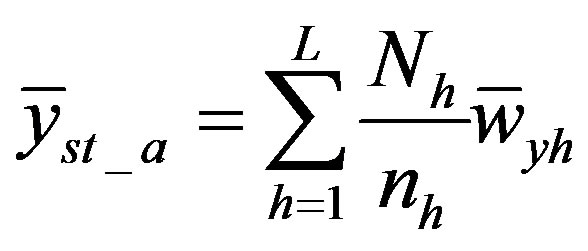 (1)
(1)
where
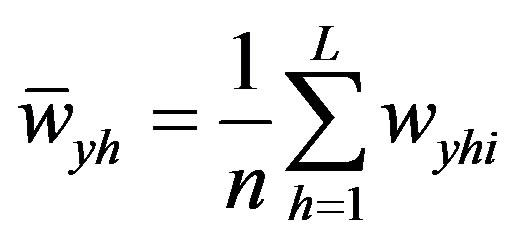
The variance of  is
is
 (2)
(2)
where
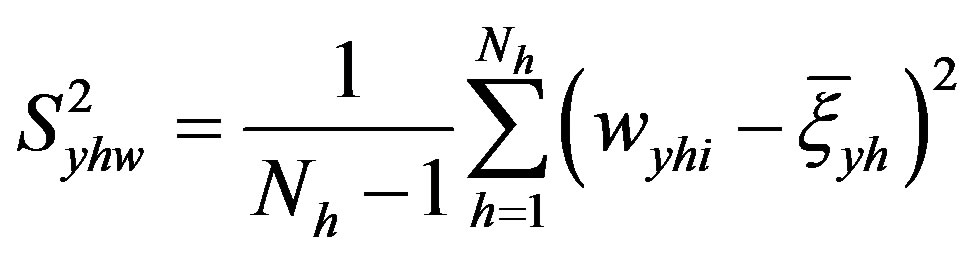
and
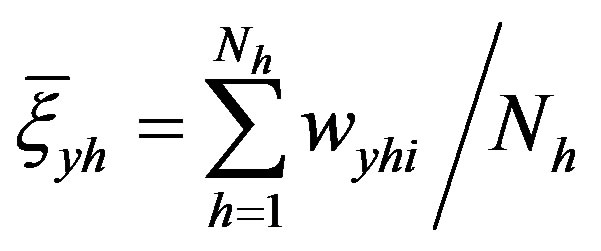 .
.
The estimate of  is
is
 (3)
(3)
where
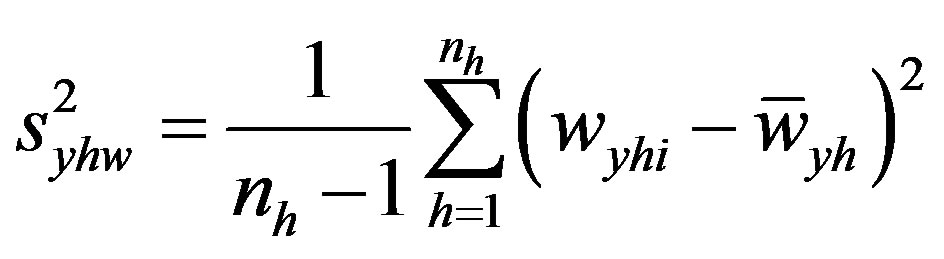 .
.
3. Propose Estimators
The estimator of the population mean in stratified adaptive cluster sampling using two auxiliary variables (x,z) is (Walid A. Abu-Dayyeh, M. S. Ahmed, R. A. Ahmed and Hassen A. Muttlak, [3]),
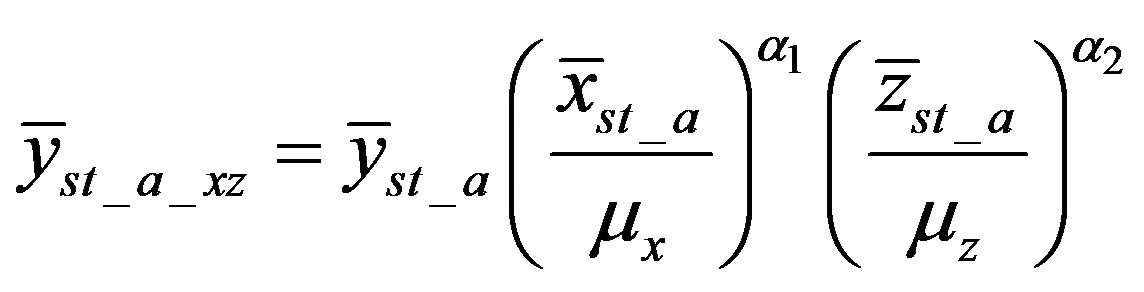 (4)
(4)
α1 = 0 and α2 = 0 is called mean per unit, α1 = −1 and  is called multivariate ratio estimator,
is called multivariate ratio estimator, 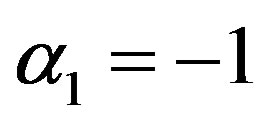 and
and  is called multivariate ratio estimator, α1 = 1 and
is called multivariate ratio estimator, α1 = 1 and 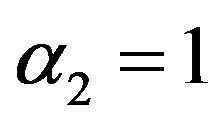 is called multivariate product estimator,
is called multivariate product estimator, 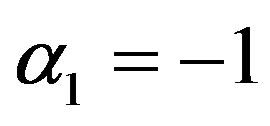 and
and 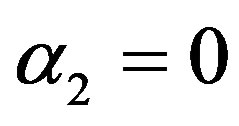 is called ratio estimator using
is called ratio estimator using ,
,  and
and 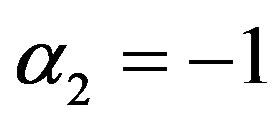 is called ratio estimator using
is called ratio estimator using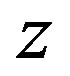 ,
,  and
and 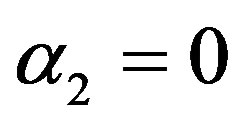 is called product estimator using
is called product estimator using 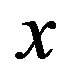 and
and 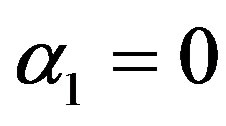 and
and  is called product estimator using
is called product estimator using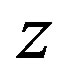 .
.
Let
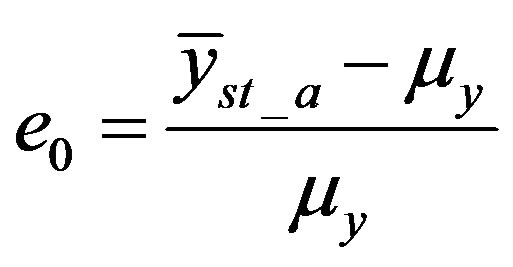 ,
, 
and
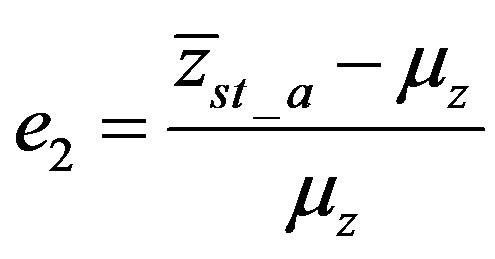
So


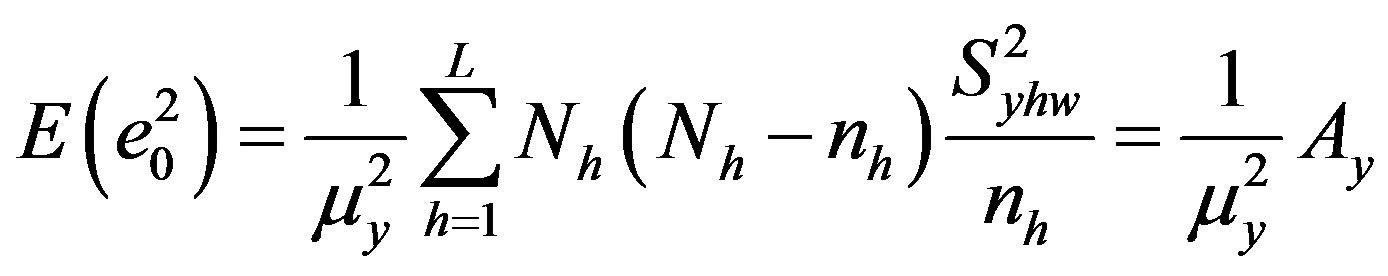 ,
,

Thus
 ,
, 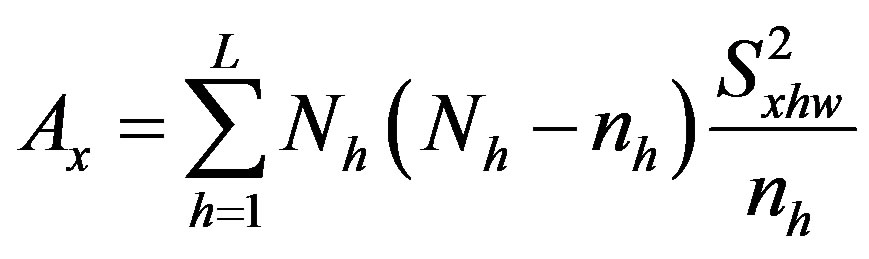
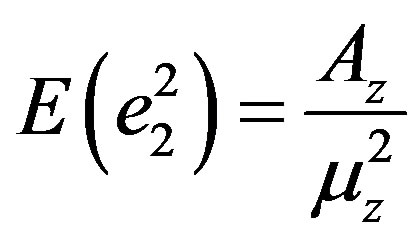 ,
,  ,
,
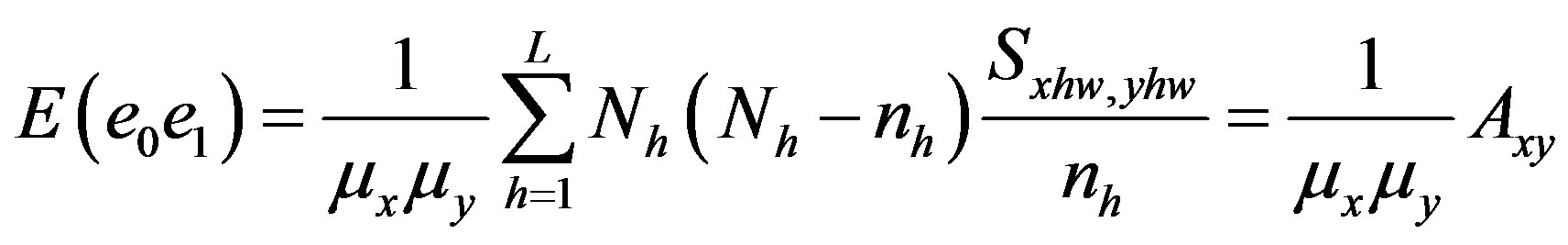

and
 .
.
So,


To find 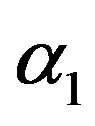 and
and 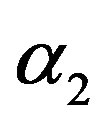 which minimizes
which minimizes 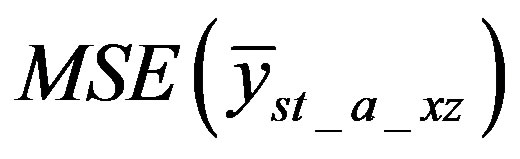 take partial derivative of
take partial derivative of 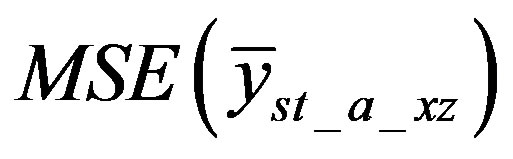 with respect to
with respect to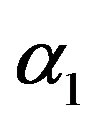 ,
, 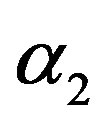 and set it equal to zero.
and set it equal to zero.
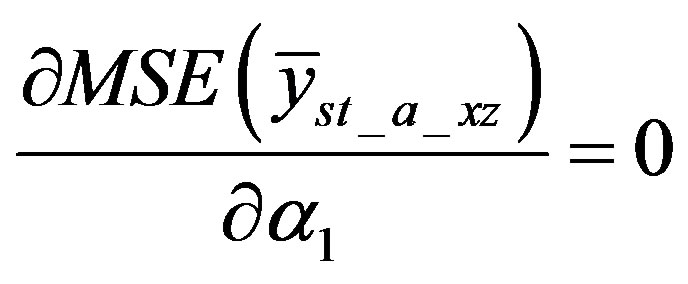
and
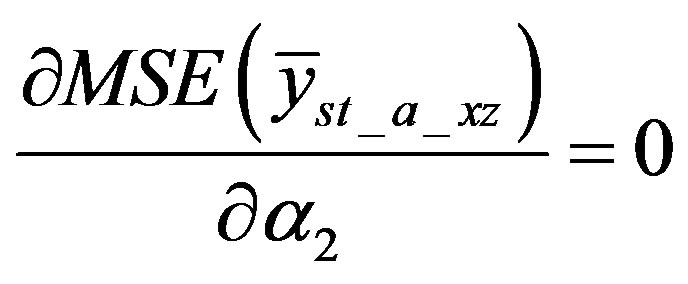
So the optimum values of  and
and 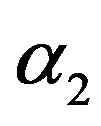 are
are
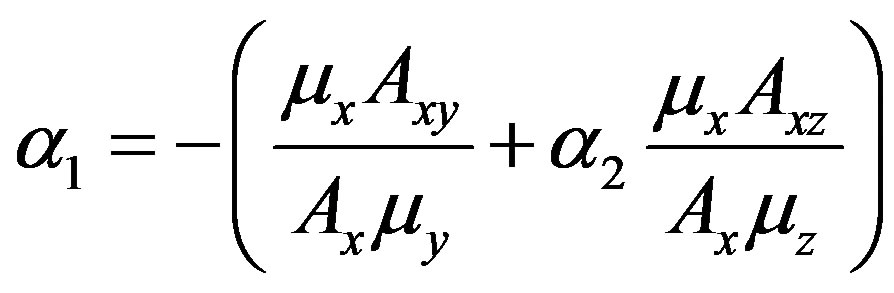
and

The estimate of 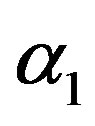 is
is
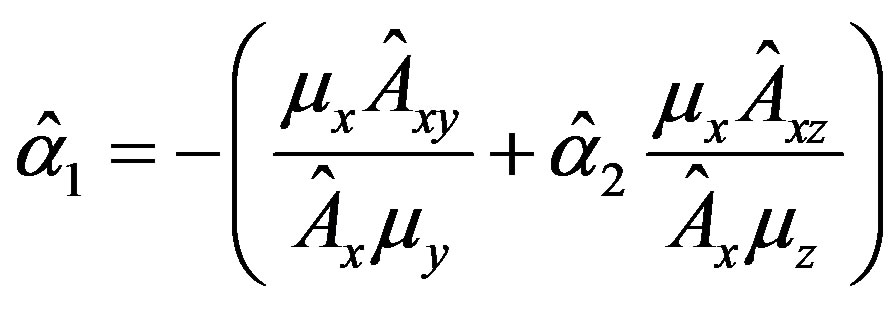
and the estimate of  is
is

where
 ,
,
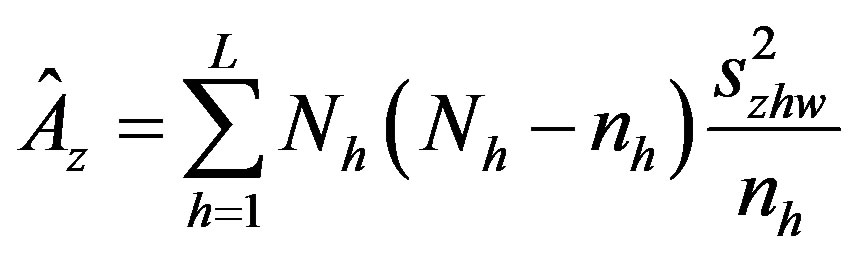 ,
,
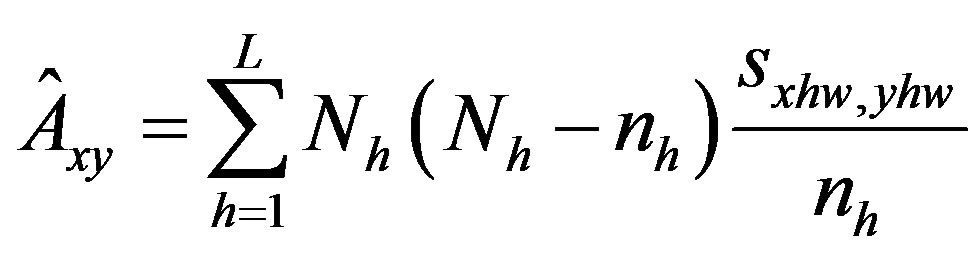 ,
,

and
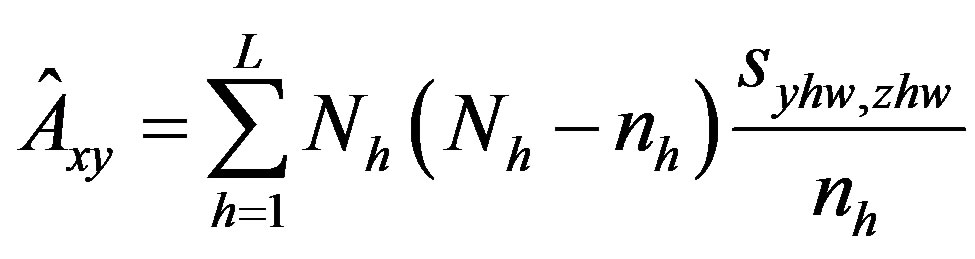 .
.
4. Simulation Study
This section, the simulation x-values z-values and y-values from Chutiman, N. and Kumphon, B. [4] were studied. The data partition into 4 stratum. The stratum size is 20 × 5 = 100 units. The populations were shown in Figures 2-4. Sample of units is selected by simple random sampling without replacement. The y-values are obtained for keeping the sample network. In each the sample network, the x-values and z-values are obtained. The condition for added units in the sample is defined by .
.
For each estimator 5000 iterations were performed to obtain an accuracy estimate. Initial SRS sizes were varied 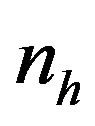 = 5, 10, 15, 20 and 30 were used. The estimated mean square error of the estimate mean is
= 5, 10, 15, 20 and 30 were used. The estimated mean square error of the estimate mean is
 where
where 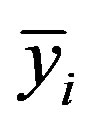 is the value for the relevant estimator for sample
is the value for the relevant estimator for sample .
.
The estimate of the mean square of the estimators  are shown in Table 1, where
are shown in Table 1, where 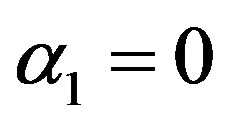 and
and  is called
is called 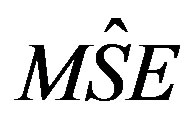 of mean per unit,
of mean per unit,  and
and 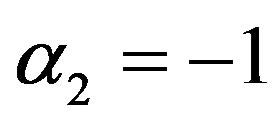 is called
is called 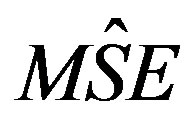 of multivariate ratio estimator,
of multivariate ratio estimator, 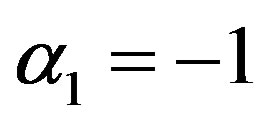 and
and  is called
is called 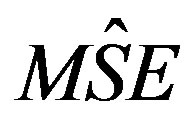 of multivariate ratio estimator,
of multivariate ratio estimator, 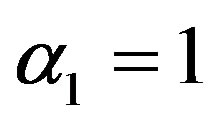 and
and  is called
is called 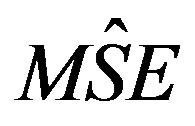 of multivariate product estimator,
of multivariate product estimator,  and
and 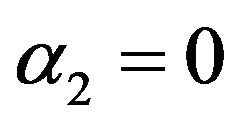 is called
is called 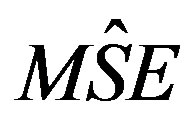 of ratio estimator using
of ratio estimator using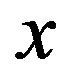 ,
,  and
and  is called
is called  of ratio estimator using
of ratio estimator using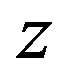 ,
, 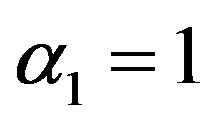 and
and  is called
is called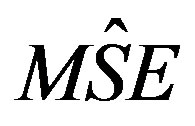 of product estimator using
of product estimator using 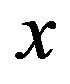 and
and 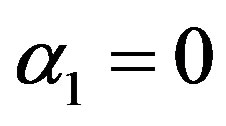 and
and 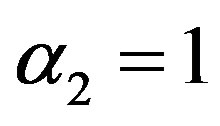 is called
is called  of product estimator using
of product estimator using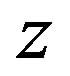 .
.
5. Conclusion
Stratified adaptive cluster sampling is an efficient method for sampling rare and hidden clustered populations. The numerical study showed that if the variable of in-
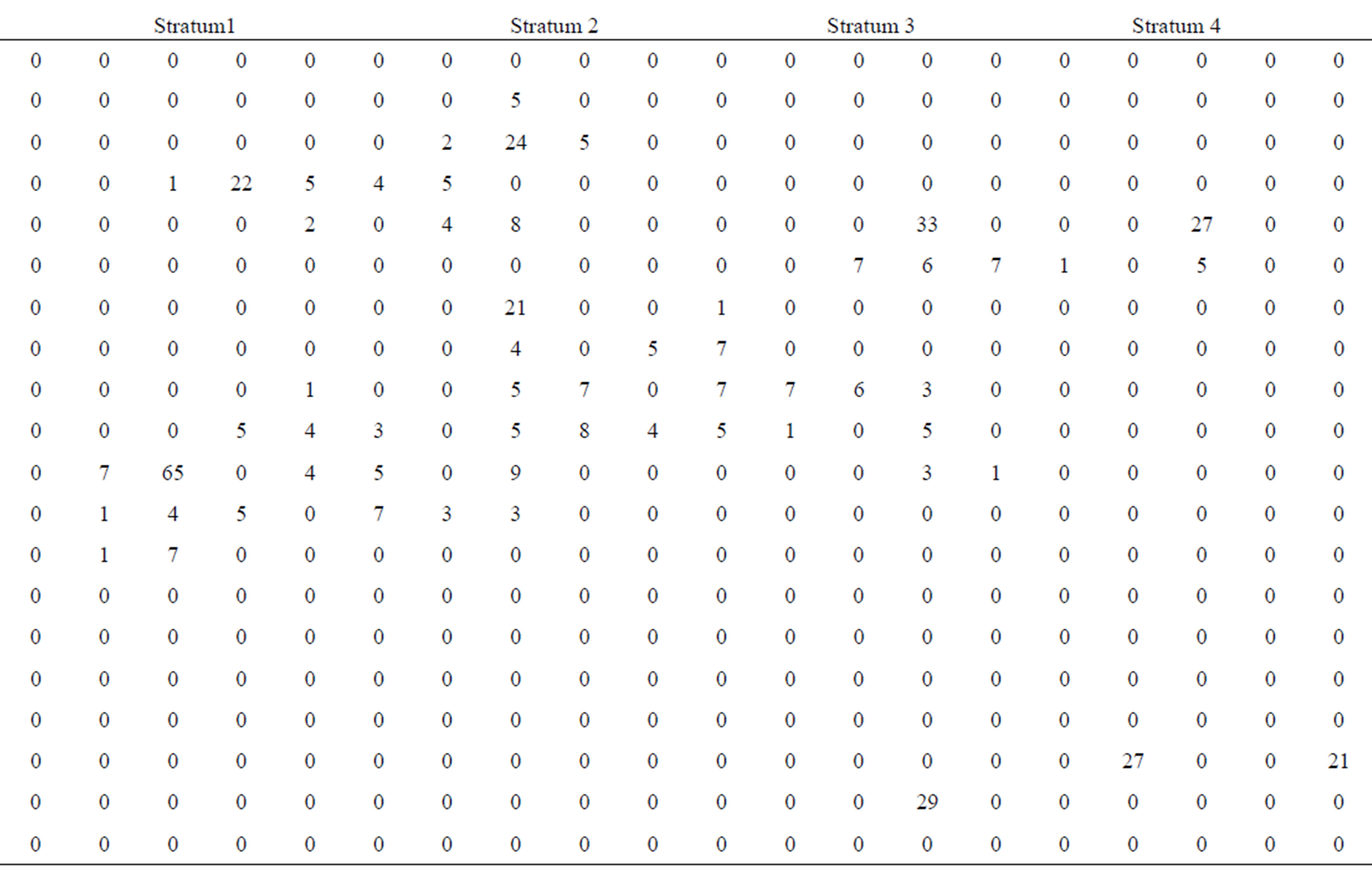
Figure 2. Y values.
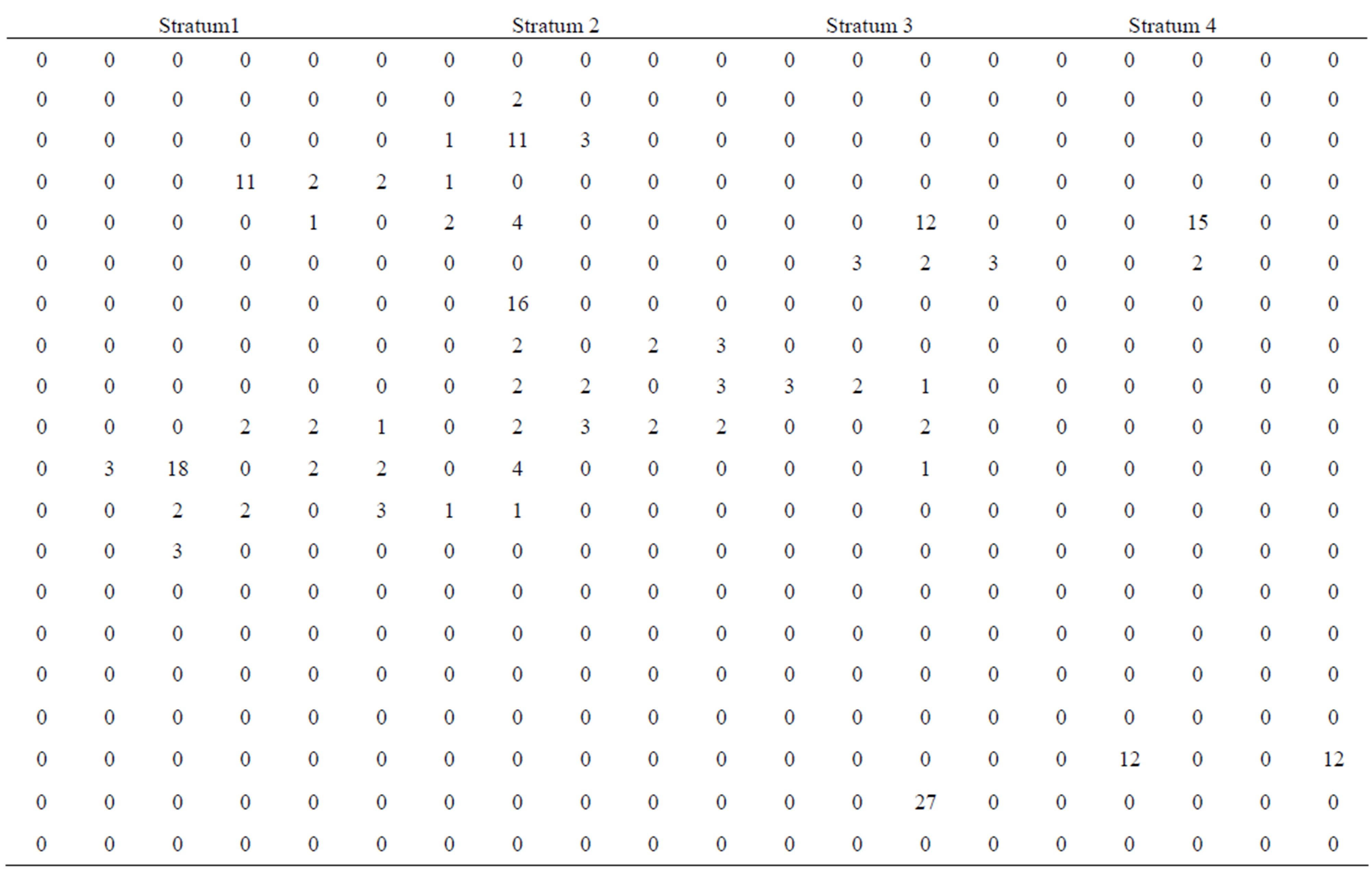
Figure 3. X values.

Figure 4. Z values.
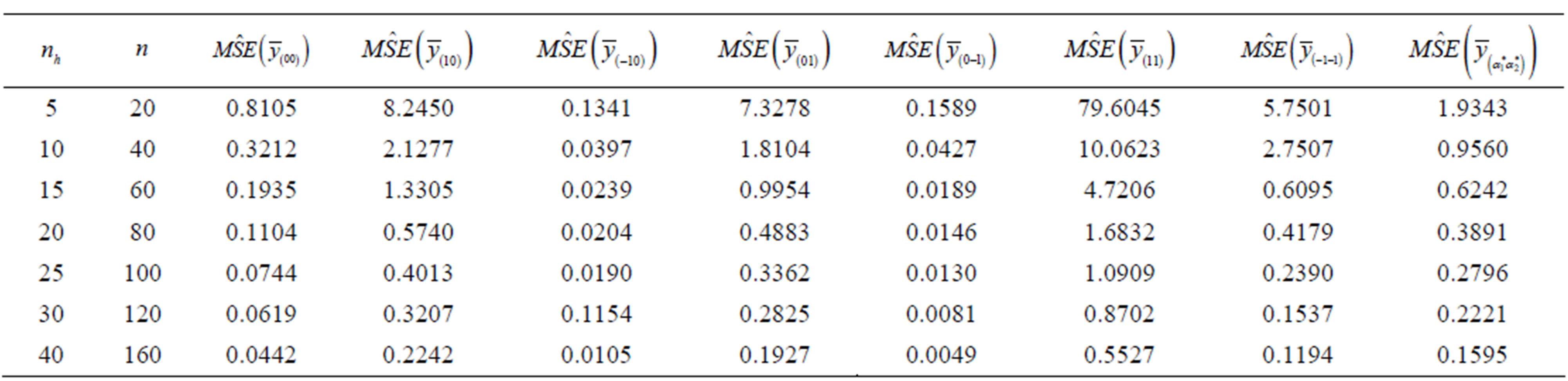
Table 1. The estimate mean square error of the estimators.
terest  and the auxiliary variables
and the auxiliary variables  have high positive correlation then the estimate of the mean square error of the ratio estimators is less than the estimate of the mean square error of the product estimator. The estimators which use only one auxiliary variable were better than the estimators which use two auxiliary variables.
have high positive correlation then the estimate of the mean square error of the ratio estimators is less than the estimate of the mean square error of the product estimator. The estimators which use only one auxiliary variable were better than the estimators which use two auxiliary variables.
6. Acknowledgements
This research was supported by Faculty of science Mahasarakham University, Thailand. We would also like to profoundly thank Mr. Paveen Chutiman for his programming advice.
REFERENCES
- S. K. Thompson, “Adaptive Cluster Sampling,” Journal of the American Statistical Association, Vol. 85, No. 412, 1990, pp. 1050-1059. doi:10.1080/01621459.1990.10474975
- S. K. Thompson and G. A. F. Seber, “Adaptive Sampling,” Wiley, New York, 1996.
- W. A. Abu-Dayyeh, M. S. Ahmed, R. A. Ahmed and H. A. Muttlak, “Some Estimators of a Finite Population Mean Using Auxiliary Information,” Applied Mathematics and Computation, Vol. 139, No. 2-3, 2003, pp. 287- 298. doi:10.1016/S0096-3003(02)00180-7
- N. Chutiman and B. Kumphon, “Ratio Estimator Using Two Auxiliary Variables for Adaptive Cluster Sampling,” Journal of the Thai Statistical Association, Vol. 6, No. 2, 2008, pp. 241-256.
NOTES
*Corresponding author.

