Open Journal of Statistics
Vol.3 No.2(2013), Article ID:30701,9 pages DOI:10.4236/ojs.2013.32015
The Expected Discounted Tax Payments on Dual Risk Model under a Dividend Threshold*
1College of Sciences, Jiangxi Agricultural University, Nanchang, China
2School of Mathematics and Statistics, Nanjing Audit University, Nanjing, China
Email: liuzhang1006@163.com, #zhangailiwh@126.com
Copyright © 2013 Zhang Liu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 19, 2012; revised December 20, 2012; accepted January 3, 2013
Keywords: Dual Risk Model; Expected Discounted Tax Payments; Dividend; Threshold Strategy
ABSTRACT
In this paper, we consider the dual risk model in which periodic taxation are paid according to a loss-carry-forward system and dividends are paid under a threshold strategy. We give an analytical approach to derive the expression of gδ(u) (i.e. the Laplace transform of the first upper exit time). We discuss the expected discounted tax payments for this model and obtain its corresponding integro-differential equations. Finally, for Erlang (2) inter-innovation distribution, closedform expressions for the expected discounted tax payments are given.
1. Introduction
Consider the surplus process of an insurance portfolio
 (1.1)
(1.1)
which is dual to the classical Cramér-Lundberg model in risk theory that describes the surplus at time , where
, where 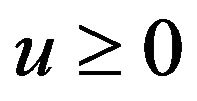 is the initial capital, the constant
is the initial capital, the constant 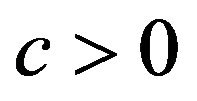 is the rate of expenses, and
is the rate of expenses, and 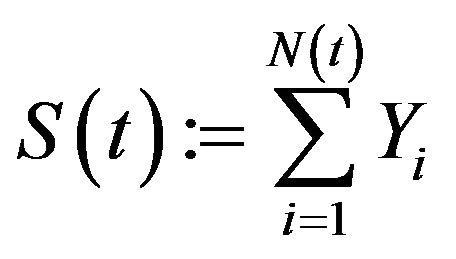 is aggregate profits process with the innovation number process
is aggregate profits process with the innovation number process 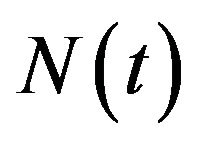 being a renewal process whose inter-innovation times
being a renewal process whose inter-innovation times 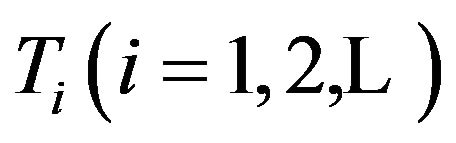 have common distribution
have common distribution . We also assume that the innovation sizes
. We also assume that the innovation sizes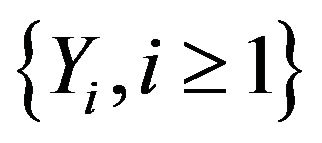 , independent of
, independent of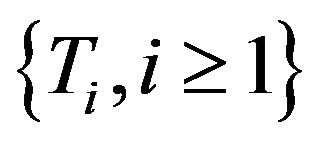 , forms a sequence of i.i.d. exponentially distributed random variables with exponential parameter
, forms a sequence of i.i.d. exponentially distributed random variables with exponential parameter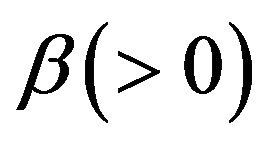 . There are many possible interpretations for this model. For example, we can treat the surplus as the amount of capital of a business engaged in research and development. The company pays expenses for research, and occasional profit of random amounts arises according to a Poisson process.
. There are many possible interpretations for this model. For example, we can treat the surplus as the amount of capital of a business engaged in research and development. The company pays expenses for research, and occasional profit of random amounts arises according to a Poisson process.
Due to its practical importance, the issue of dividend strategies has received remarkable attention in the literature. De Finetti [1] considered the surplus of the company that is a discrete process and showed that the optimal strategy to maximize the expectation of the discounted dividends must be a barrier strategy. Since then, researches on dividend strategies has been carried out extensively. For some related results, the reader may consult the following publications therein: Bühlmann [2], Gerber [3], Gerber and Shiu [4,5], Lin et al. [6], Lin and pavlova [7], Dickson and Waters [8], Albrecher et al. [9], Dong et al. [10] and Ng [11]. Recently, quite a few interesting papers have been discussing risk models with tax payments of loss carry forward type. Albrecher et al. [12] investigated how the loss-carry forward tax payments affect the behavior of the dual process (1.1) with general inter-innovation times and exponential innovation sizes. More results can be seen in Albrecher and Hipp [13], Albrecher et al. [14], Ming et al. [15], Wang and Hu [16] and Liu et al. [17,18].
Now, we consider the model (1.1) under the additional assumption that tax payments are deducted according to a loss-carry forward system and dividends are paid under a threshold strategy. We rewrite the objective process as . that is, the insurance company pays tax at rate
. that is, the insurance company pays tax at rate  on the excess of each new record high of the surplus over the previous one; at the same time, dividends are paid at a constant rate
on the excess of each new record high of the surplus over the previous one; at the same time, dividends are paid at a constant rate ![]() whenever the surplus of an insurance portfolio is more than b and otherwise no dividends are paid. Then the surplus process of our model
whenever the surplus of an insurance portfolio is more than b and otherwise no dividends are paid. Then the surplus process of our model 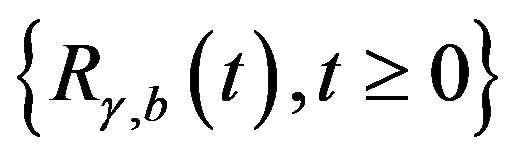 can be expressed as
can be expressed as
 (1.2)
(1.2)
for , with
, with . where
. where  is the indicator function of event
is the indicator function of event  and
and  is the surplus immediately before time
is the surplus immediately before time .
.
For practical consideration, we assume that the positive safety loading condition
 (1.3)
(1.3)
holds all through this paper. The time of ruin is defined as 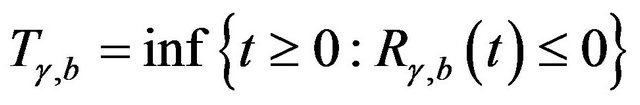 with
with  if
if
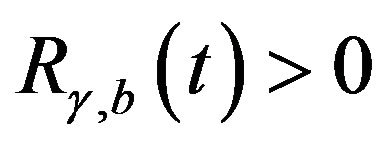 for all
for all .
.
For initial surplus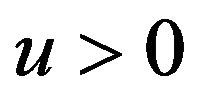 , let
, let  be the present value of all dividends until ruin, and
be the present value of all dividends until ruin, and  is the discount factor. Denote by
is the discount factor. Denote by  the expectation of
the expectation of , that is,
, that is,
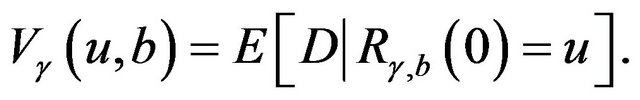 (1.4)
(1.4)
It needs to be mentioned that we shall drop the subscript 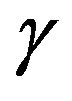 whenever
whenever  is zero.
is zero.
The rest of this paper is organized as follows. In Section 2, We derive the expression of 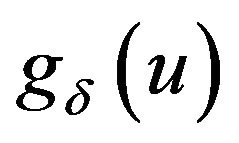 (i.e. the Laplace transform of the first upper exit time). We also discuss the expected discounted tax payments for this model and obtain its satisfied integro-differential equations. Finally, for Erlang (2) inter-innovation distribution, closed-form expressions for the the expected discounted tax payments are given.
(i.e. the Laplace transform of the first upper exit time). We also discuss the expected discounted tax payments for this model and obtain its satisfied integro-differential equations. Finally, for Erlang (2) inter-innovation distribution, closed-form expressions for the the expected discounted tax payments are given.
2. Main Results and Proofs
Let  denote the Laplace transform of the upper exit time
denote the Laplace transform of the upper exit time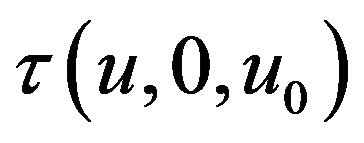 , which is the time until the risk process
, which is the time until the risk process 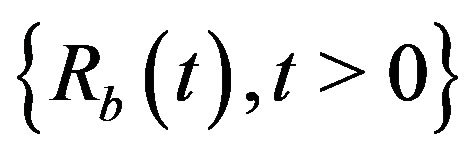 starting with initial capital
starting with initial capital  up-crosses the level
up-crosses the level  for the first time without leading to ruin before that event. In particular,
for the first time without leading to ruin before that event. In particular, ![]() is the probability that the process
is the probability that the process 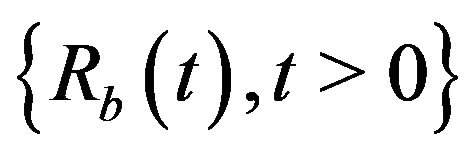 up-crosses the level
up-crosses the level  before ruin.
before ruin.
For general innovation waiting times distribution, one can derive the integral equations for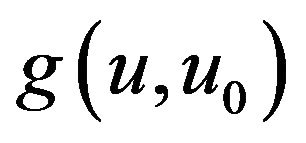 . When
. When ,
,
 (2.1)
(2.1)
When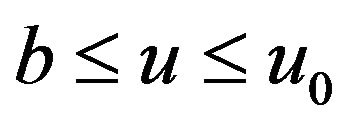 ,
,
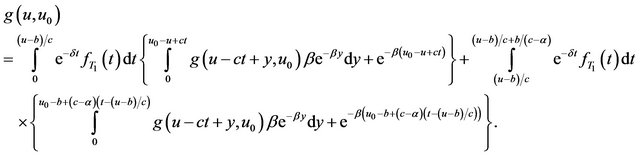 (2.2)
(2.2)
It follows from Equation (2.1) and from Equation (2.2) that 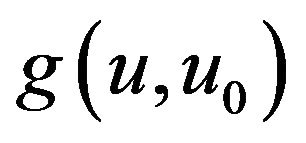 is continuous on
is continuous on 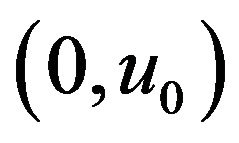 as a function of
as a function of ![]() and that
and that
 (2.3)
(2.3)
For certain distributions , one can derive integrodifferential equations for
, one can derive integrodifferential equations for 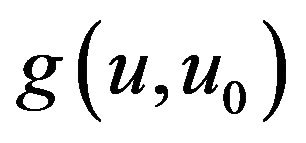 and
and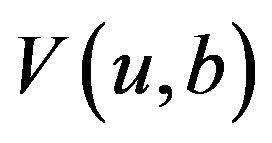 . Let us assume that the i.i.d innovation waiting times have a common generalized Erlang
. Let us assume that the i.i.d innovation waiting times have a common generalized Erlang distribution, i.e. the
distribution, i.e. the![]() ’s are distributed as the sum of n independent and exponentially distributed r.v.’s
’s are distributed as the sum of n independent and exponentially distributed r.v.’s 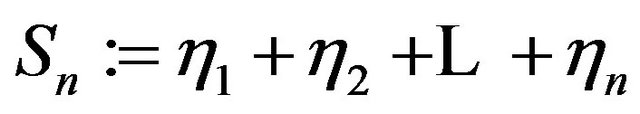 with
with  having exponential parameters
having exponential parameters .
.
The following theorem 2.1 gives the integro-differential equations for  when
when![]() ’s have a generalized Erlang
’s have a generalized Erlang distribution.
distribution.
Theorem 2.1 Let  and
and  denote the identity operator and differentiation operator respectively. Then
denote the identity operator and differentiation operator respectively. Then 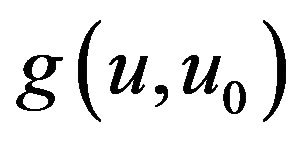 satisfies the following equation for
satisfies the following equation for 
 (2.4)
(2.4)
and
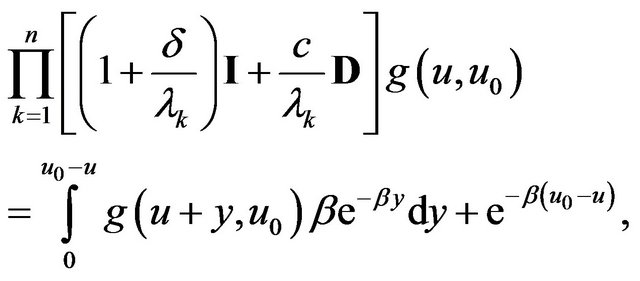 (2.5)
(2.5)
for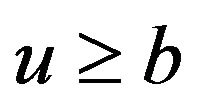 .
.
Proof First, we rewrite  as
as 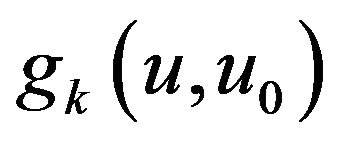 when
when
 with
with 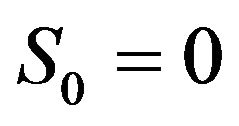 in the surplus process (1.2)
in the surplus process (1.2)
with . Thus, we have
. Thus, we have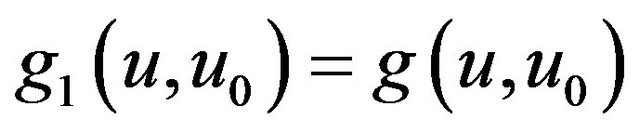 . When
. When ,
,
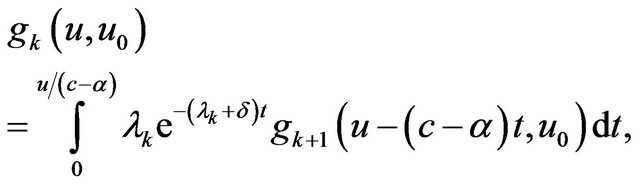 (2.6)
(2.6)
for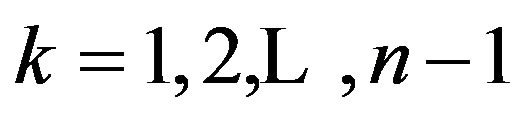 , and
, and
 (2.7)
(2.7)
By changing variables in from Equation (2.6) and from Equation (2.7), we have for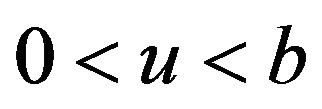 ,
,
 (2.8)
(2.8)
for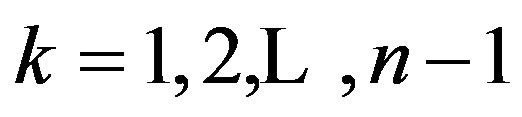 , and
, and
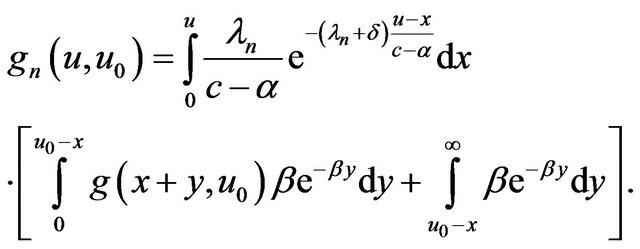 (2.9)
(2.9)
Then, differentiating both sides of from Equation (2.8) and from Equation (2.9) with respect to![]() , one gets
, one gets
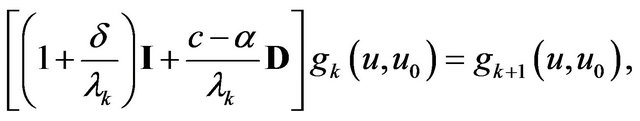 (2.10)
(2.10)
for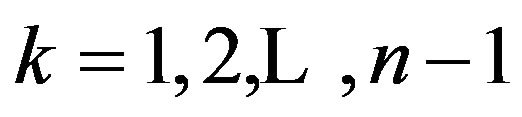 , and
, and
 (2.11)
(2.11)
Using from Equation (2.10) and from Equation (2.11), we can derive from Equation (2.4) for  on
on .
.
Similar to from Equation (2.6) and Equation (2.7), we have for 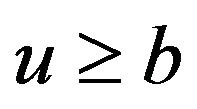
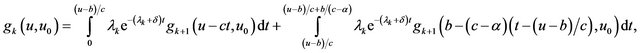 (2.12)
(2.12)
for , and
, and
 (2.13)
(2.13)
Again, by changing variables in Equation (2.12) and Equation (2.13) and then differentiating them with respect to![]() , we obtain for
, we obtain for 
 (2.14)
(2.14)
for , and
, and
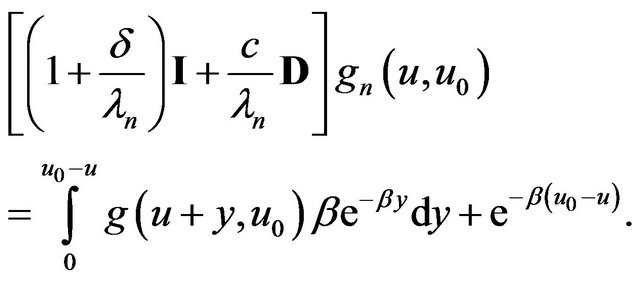 (2.15)
(2.15)
Using Equation (2.14) and Equation (2.15), we obtain Equation (2.5) for 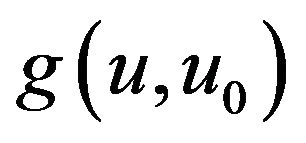 on
on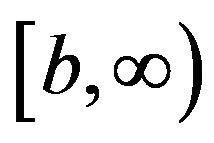 .□
.□
It needs to be mentioned that from the proof of Lemma 2.1, we know that

Therefore, Equations (2.10), (2.11), (2.14) and (2.15) yield
 (2.16)
(2.16)
Remark 2.1 Using a similar argument to the one used in Lemma 2.1, one can get that when the innovation waiting times follow a common generalized Erlang distribution, the expected discounted dividend payments
distribution, the expected discounted dividend payments 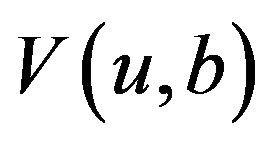 satisfies the following integro-differential equation (see Liu et al. [17]).
satisfies the following integro-differential equation (see Liu et al. [17]).
 (2.17)
(2.17)
and
 (2.18)
(2.18)
with
 (2.19)
(2.19)
In addition, the boundary conditions for 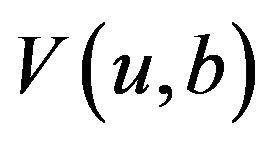 are as follows:
are as follows:
 (2.20)
(2.20)
 (2.21)
(2.21)
with Equation (2.19).
With the preparations made above, we can now derive analytic expressions of the expected ![]() -th moment of the accumulated discounted tax payments for the surplus process
-th moment of the accumulated discounted tax payments for the surplus process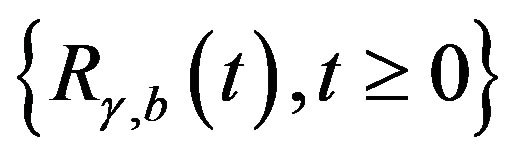 . We claim that the process
. We claim that the process
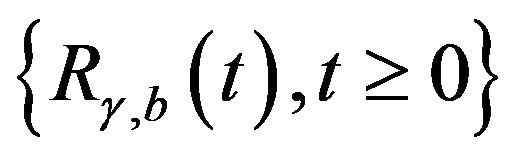 shall up-cross the initial surplus level
shall up-cross the initial surplus level ![]() at least once to avoid ruin.
at least once to avoid ruin.
Now, let
 (2.22)
(2.22)
denote the Laplace transform of the first upper exit time , which is the time until the risk process
, which is the time until the risk process
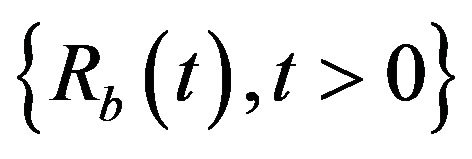 starting with initial capital
starting with initial capital ![]() reaches a new record high for the first time without leading to ruin before that event. In particular,
reaches a new record high for the first time without leading to ruin before that event. In particular, ![]() is the probability that the process
is the probability that the process 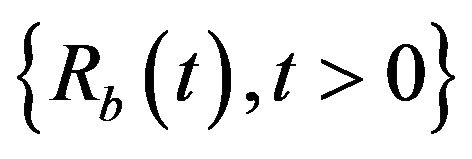 reaches a new record high before ruin. Then the closed-form expression of the quantity
reaches a new record high before ruin. Then the closed-form expression of the quantity 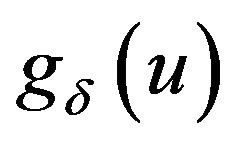 can be calculated as follows.
can be calculated as follows.
When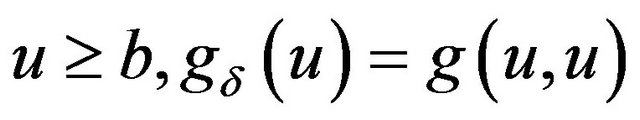 . When
. When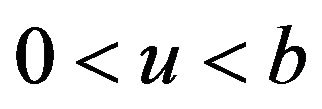 , using a simple sample path argument, we immediately have,
, using a simple sample path argument, we immediately have,

or, equivalently
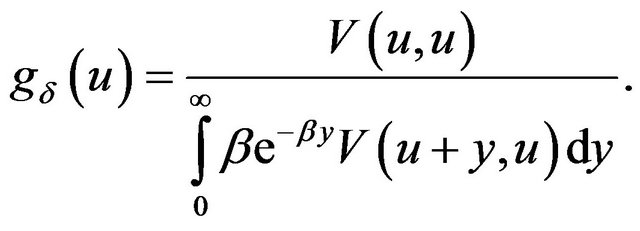 (2.23)
(2.23)
Let  and define
and define
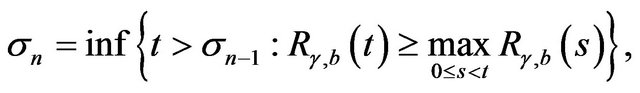 (2.24)
(2.24)
to be the ![]() -th taxation time point. Thus,
-th taxation time point. Thus,

(2.25)
denotes the ![]() -th moment of the accumulated discounted tax payments over the life time of the surplus process
-th moment of the accumulated discounted tax payments over the life time of the surplus process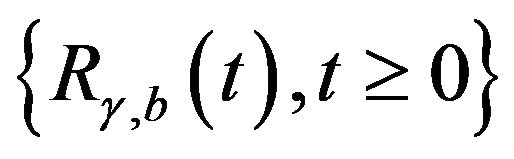 .
.
We will consider a recursive formula of 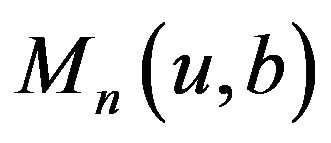 in the following theorem 2.2.
in the following theorem 2.2.
Theorem 2.2 When , we have
, we have
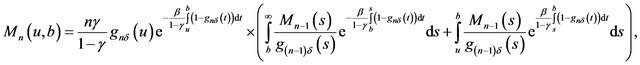 (2.26)
(2.26)
and when , we have
, we have
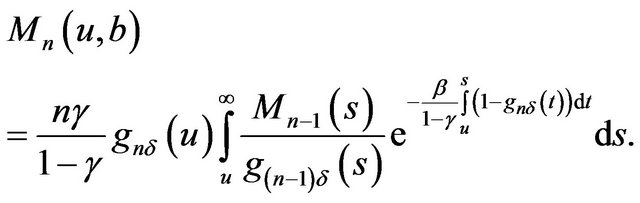 (2.27)
(2.27)
Proof Given that the after-tax excess of the surplus level over ![]() at time
at time 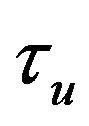 is exponentially distributed with mean
is exponentially distributed with mean  due to the memoryless property of the exponential distribution. By a probabilistic argument, one easily shows that for
due to the memoryless property of the exponential distribution. By a probabilistic argument, one easily shows that for 

(2.28)
Differentiating with respect to ![]() yields
yields
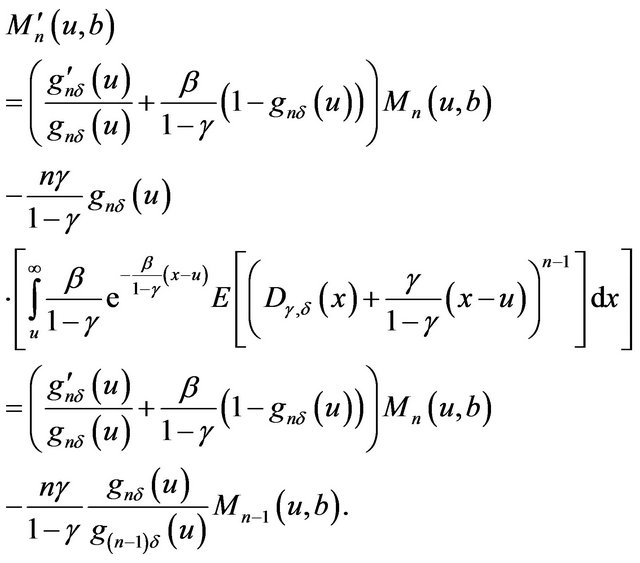
(2.29)
When , we have
, we have
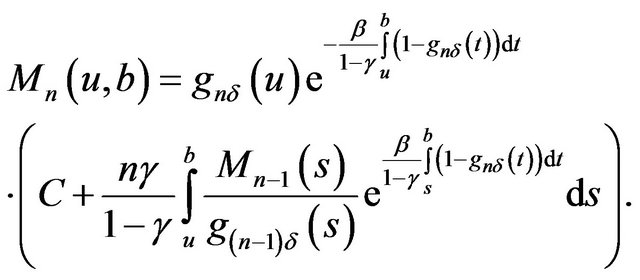 (2.30)
(2.30)
When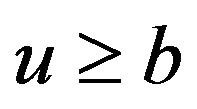 , the general solution of Equation (3.20) can be expressed as
, the general solution of Equation (3.20) can be expressed as
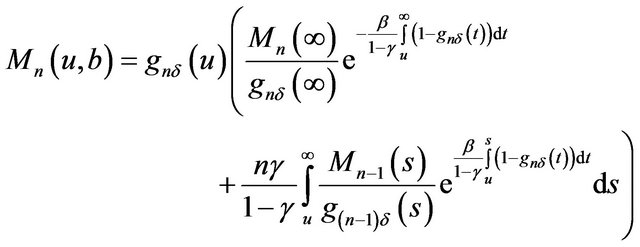
(2.31)
Due to the facts that  and
and  , we have for
, we have for 
 (2.32)
(2.32)
Now, it remains to determine the unknown constant C in Equation (3.20). The continuity of 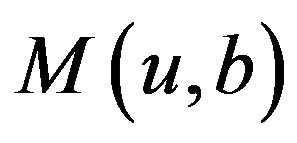 on
on 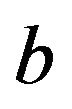 and Equation (3.22) lead to
and Equation (3.22) lead to
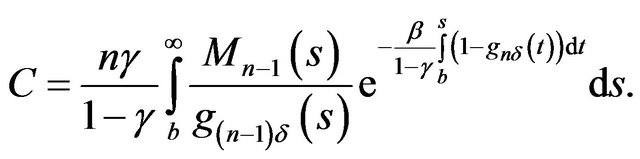 (2.33)
(2.33)
Plugging Equation (2.33) into Equation (2.30), we arrive at Equation (2.26). □
The special case 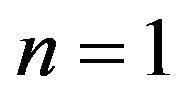 leads to an expression for the expected discounted total sum of tax payments over the life time of the risk process
leads to an expression for the expected discounted total sum of tax payments over the life time of the risk process
 (2.34)
(2.34)
for all .
.
3. Explicit Results for Erlang(2) Innovation Waiting Times
In this section, we assume that ’s are Erlang(2) distributed with parameters
’s are Erlang(2) distributed with parameters 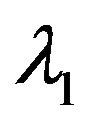 and
and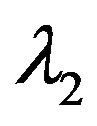 . We also assume that
. We also assume that  (without loss of generality).
(without loss of generality).
Example 3.1 Note that
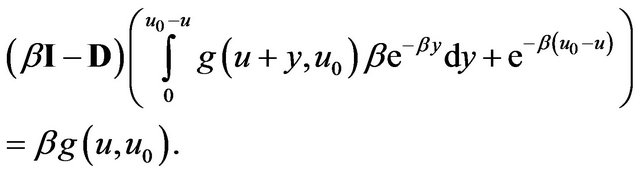 (3.1)
(3.1)
Applying the operator  to Equations (2.4) and (2.5) gives
to Equations (2.4) and (2.5) gives

(3.2)
and
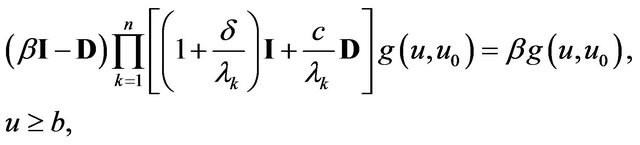
(3.3)
The characteristic equation for Equation (3.2) is
 (3.4)
(3.4)
without loss of generality, we assume that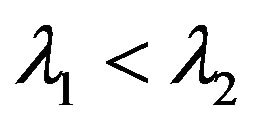 . We know that Equation (3.4) has three real roots, say
. We know that Equation (3.4) has three real roots, say ![]() and
and ![]() which satisfies
which satisfies
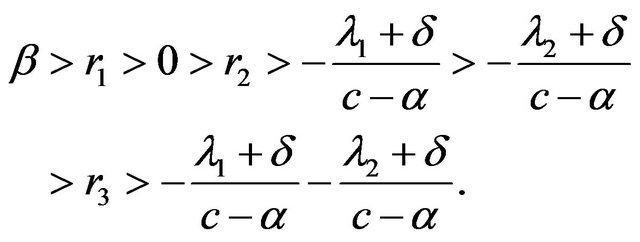
With ![]() replace
replace ![]() in Equation (3.4), we get the characteristic equation of Equation (3.3), whose roots are denoted by
in Equation (3.4), we get the characteristic equation of Equation (3.3), whose roots are denoted by  and
and ![]() with
with

Thus, we have
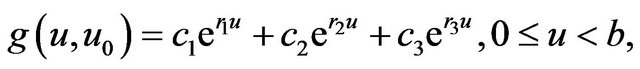 (3.5)
(3.5)
and
 (3.6)
(3.6)
where 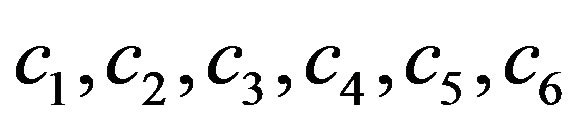 are arbitrary constants. To determine the arbitrary constants, we insert Equations (3.5) and (3.6) into Equation (2.3) and obtain
are arbitrary constants. To determine the arbitrary constants, we insert Equations (3.5) and (3.6) into Equation (2.3) and obtain
 (3.7)
(3.7)
and
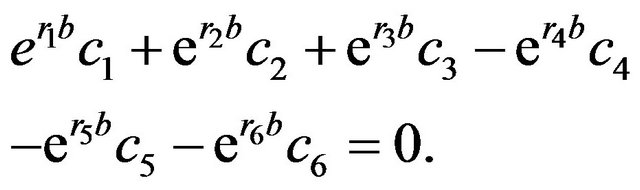 (3.8)
(3.8)
Apply Equation (2.10) together with Equations (2.3) and (3.5) when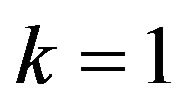 , we get
, we get
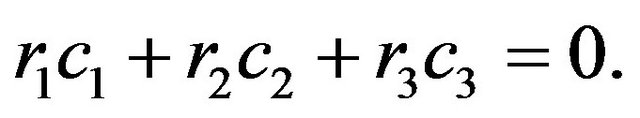 (3.9)
(3.9)
Insert Equation (3.5) into Equation (2.4), we have
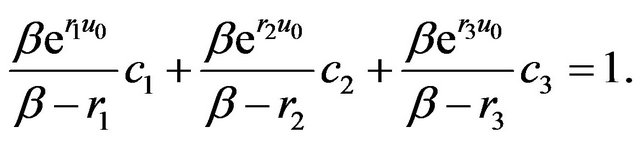 (3.10)
(3.10)
In addition, plugging Equations (3.5) and (3.6) into Equation (2.16) yields
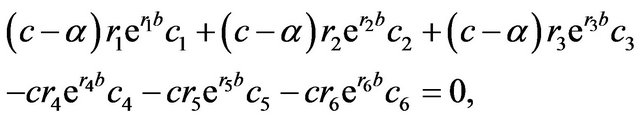 (3.11)
(3.11)
and
 (3.12)
(3.12)
Some calculations give
 (3.13)
(3.13)
with
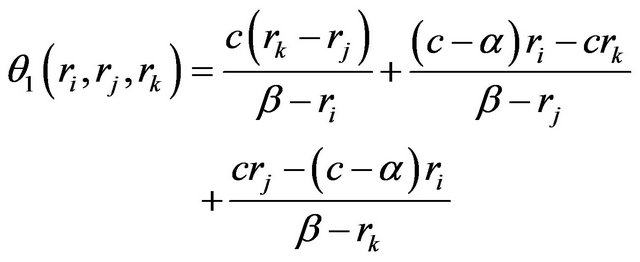 (3.14)
(3.14)
Remark 3.1 Now, we give the explicit results for
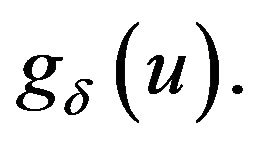 By Equations (3.6) and (3.13), we have for
By Equations (3.6) and (3.13), we have for 
 (3.15)
(3.15)
with
 (3.16)
(3.16)
For , using the explicit expressions of
, using the explicit expressions of  in Liu et al. [17], we obtain
in Liu et al. [17], we obtain
 (3.17)
(3.17)
with
 (3.18)
(3.18)
where

and

We point out that when the innovation times are exponentially distributed, one can follow the same steps to get the explicit expressions of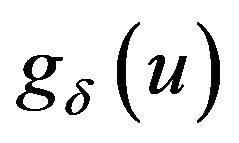 , which coincide with the results in Albrecher et al. (2008).
, which coincide with the results in Albrecher et al. (2008).
Example 3.2 (The expected discounted tax payments.) Following from Equation (2.34) of Theorem 2.2 and Remark 3.1, we have for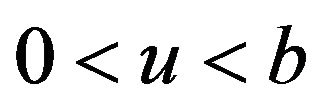 ,
,
 (3.19)
(3.19)
And, for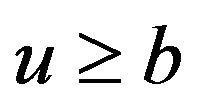 , we have
, we have
 (3.20)
(3.20)
Then we can get that when ’s are Erlang (2) distributed with parameters
’s are Erlang (2) distributed with parameters 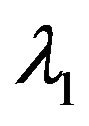 and
and , the expresses of
, the expresses of  can be given by Equations (3.15) and (3.17) and the expected discounted tax payments can be given by Equation (3.20).
can be given by Equations (3.15) and (3.17) and the expected discounted tax payments can be given by Equation (3.20).
4. Acknowledgements
The author would like to thank Professor Ruixing Ming and Professor Guiying Fang for their useful discussions and valuable suggestions.
REFERENCES
- B. De Finetti, “Su un’Impostazione Alternativa Della Teoria Collettiva del Rischio,” Proceedings of the Transactions of the XV International Congress of Actuaries, New York, 1957, pp. 433-443.
- H. Bühlmann, “Mathematical Methods in Risk Theory,” Springer-Verlag, New York, Heidelberg. 1970.
- H. Gerber, “An Introduction to Mathematical Risk Theory. S. S. Huebner Foundation,” University of Pennsylvania, Philadelphia. 1979.
- H. Gerber and E. Shiu, “On the Time Value of Ruin,” North American Actuarial Journal, Vol. 2, No. 1, 1998, pp. 48-78. doi:10.1080/10920277.1998.10595671
- H. Gerber and E. Shiu, “On Optimal Dividend Strategies in the Compound Poisson Model,” Preprint, 2006.
- X. S. Lin, G. E. Willmot and S. Drekic, “The Classical Risk Model with a Constant Dividend Barrier: Analysis of the Gerber-Shiu Discounted Penalty Function,” Insurance: Mathematics and Economics, Vol. 33, No. 3, 2003, pp. 551-566. doi:10.1016/j.insmatheco.2003.08.004
- X. S. Lin and K. P. Pavlova, “The Compound Poisson Risk Model with a Threshold Dividend Strategy,” Insurance: Mathematics and Economics, Vol. 38, No. 1, 2005, pp. 57-80. doi:10.1016/j.insmatheco.2005.08.001
- D. C. M. Dickson and H. R. Waters, “Some Optimal Dividend Problems,” ASTIN Bulletin, Vol. 34 No. 1, 2004, pp. 49-74. doi:10.2143/AST.34.1.504954
- H. Albrecher, J. Hartinger and R. Tichy, “On the Distribution of Dividend Payments and the Discounted Penalty Function in a Risk Model with Linear Dividend Barrier,” Scandinavian Actuarial Journal, Vol. 2005, No. 2, 2005, pp. 103-126. doi:10.1080/03461230510006946
- Y. H. Dong, G. J. Wang and K. C. Yuen, “On the Renewal Risk Model under a Threshold Strategy,” Journal of Computational and Applied Mathematics, Vol. 230, No. 1, 2009, pp. 22-33.
- C. Y. Ng Andrew, “On a Dual Model with a Dividend Threshold,” Insurance: Mathematics and Economics, Vol. 44, No. 2, 2009, pp. 315-324. doi:10.1016/j.insmatheco.2008.11.011
- H. Albrecher, A. Badescu and D. Landriault, “On the Dual Risk Model with Taxation,” Insurance: Mathematics and Economics, Vol. 42, No. 3, 2008, pp. 1086-1094. doi:10.1016/j.insmatheco.2008.02.001
- H. Albrecher and C. Hipp, “Lundberg’s Risk Process with Tax,” Blätter der DGVFM, Vol. 28, No. 1, 2007, pp. 13- 28. doi:10.1007/s11857-007-0004-4
- H. Albrecher, J. Renaud and X. W. Zhou, “A Lévy Insurance Risk Process with Tax,” Journal of Applied Probability, Vol. 45, No. 2, 2008, pp. 363-375. doi:10.1239/jap/1214950353
- R. X. Ming, W. Y. Wang and L. Q. Xiao, “On the Time Value of Absolute Ruin with Tax,” Insurance: Mathematics and Economics, Vol. 46, No. 1, 2010, pp. 67-84. doi:10.1016/j.insmatheco.2009.09.004
- W. Y. Wang and Y. J. Hu, “Optimal Loss-Carry-Forward Taxation for the Levy Risk Model,” Insurance: Mathematics and Economics, Vol. 50, No. 1, 2012, pp. 121-130. doi:10.1016/j.insmatheco.2011.10.011
- Z. Liu, W. Y. Wang and R. X. Ming, “The Threshold Dividend Strategy on a Class of Dual Model with Tax Payments,” Journal of University of Sience and Technology of China, 2013, in Press.
- Z. Liu, R. X. Ming, W. Y. Wang and X. Y. Song, “The Threshold Dividend Strategy in the Dual Risk Model Perturbed by Diffusion,” Journal of University of Sience and Technology of China, Vol. 42, No. 6, 2012, pp. 475- 481.
NOTES
*Supposed by the Jiangxi Agricultural University Youth Science Foundation (No. 09003326).
#Corresponding author.

