Open Journal of Statistics
Vol.1 No.2(2011), Article ID:6349,5 pages DOI:10.4236/ojs.2011.12012
On Asymptotic Properties of AIC Variants with Applications
University of Cyprus & National Technical University of Athens, Athens, Greece
E-mail: alex@ucy.ac.cy, mattheouk@cytanet.com.cy, vonta@math.ntua.gr
Received May 24, 2011; revised June 15, 2011; accepted June 23, 2011
Keywords: AIC, Jackknife, Censored Regression Model, Asymptotic Efficiency
Abstract
In statistical modeling, the investigator is frequently confronted with the problem of selecting an appropriate model from a general class of candidate models. In recent years, various model selection procedures that can be used for the selection of the best possible model have been proposed. The AIC criterion [1] is considered the most popular tool for model selection although many competitors have been introduced over the years. One of the main drawbacks of AIC is its tendency to favor high dimensional models namely to overestimate the true model. A second issue that needs the attention of the investigator is the presence of outlying observations in the data set the inclusion of which in the statistical analysis may lead to erroneous results. In this work we propose AIC variants to handle the above weaknesses. Furthermore the asymptotic properties of the proposed criteria are investigated and a number of applications are discussed.
1. Introduction
In this section we introduce an AIC variant that involves bootstrap-based corrections. The idea of bootstrap to improve the performance of a model was introduced by Efron [2] and discussed by others in recent years (e.g. [3] and [4]).
Assume that n pairs of observations (x1,y1),...,(xn,yn) are available from the p0-dimensional regression model
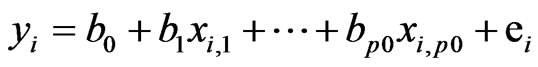
where , i = 1, 2,···, n and e~F(
, i = 1, 2,···, n and e~F(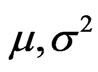 ) for a distribution function F with mean
) for a distribution function F with mean  and variance
and variance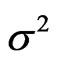 .
.
The Akaike Information Criterion (AIC) evaluated for the p-dimensional model, p < K is given by
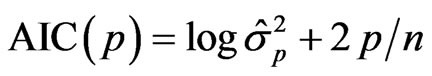 where K a pre-assigned upper bound for the true dimension p0 of the model and
where K a pre-assigned upper bound for the true dimension p0 of the model and 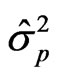 the least squares estimator of
the least squares estimator of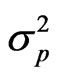 . An equally popular criterion is the so called Bayesian Information Criterion (BIC; [5]) which is defined similarly by
. An equally popular criterion is the so called Bayesian Information Criterion (BIC; [5]) which is defined similarly by
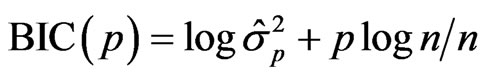 .
.
The bootstrapping algorithm for the AIC variant is defined as follows. We remove the ith observation and apply the criterion to the remaining n – 1 observations. Let 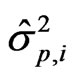 the estimator of the variance of the p-dimensional model which is based on the n – 1 remaining observations. Then, the estimate of AIC is given by
the estimator of the variance of the p-dimensional model which is based on the n – 1 remaining observations. Then, the estimate of AIC is given by
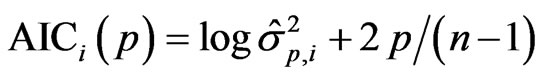 .
.
We now define the AIC average by
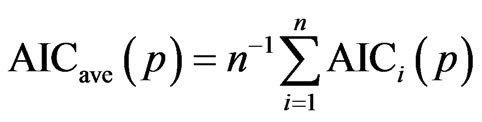 . The AIC variant is finally defined by
. The AIC variant is finally defined by
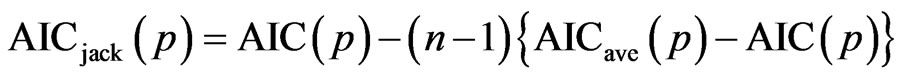 (1)
(1)
Observe that the proposed technique represents a bias correction for the original value of AIC so that the resulting variant form is a bias-corrected version of AIC. Note also that as it turns out, the proposed method can be described better by the jackknife technique rather than the traditional bootstrapping approach.
Observe that a jackknife-corrected version of BIC could be defined similarly. In particular, define the estimate of BIC based on n-1 observations as follows:
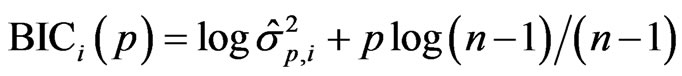 .
.
We now define the BIC average by
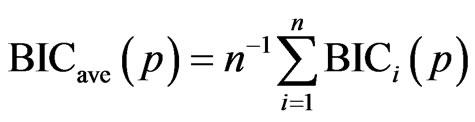 .
.
Finally, the jackknife variant of BIC is given by
 .
.
If the above adjusted approach is applied to the small sample variant AICC proposed by Hurvich and Tsai [6], the resulting AIC estimate will be:
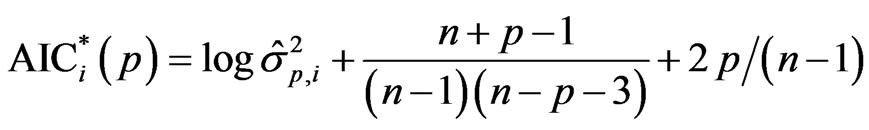
which is equivalent to
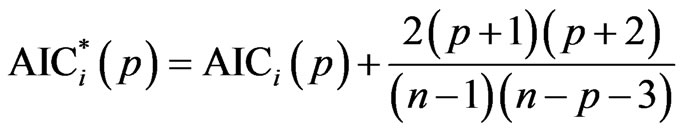 . (2)
. (2)
As a result, the average AIC and the AIC variant criterion can be defined analogously. The resulting criterion is given by
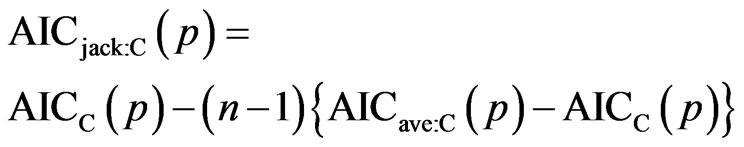
where AICave;C(p) is defined similarly to AICave(p).
It should be pointed out here that model selection criteria such as the above could be applied to a very general context not only in regression models like the ones used in this section but also in autoregression models as well as in survival models.
2. Asymptotic Properties
In this section we first establish the equivalence of AIC and all criteria proposed earlier and then investigate the asymptotic properties of the proposed criteria. The equivalence of the AIC variant given in (1) and the original AIC criterion is established in the following theorem.
Theorem 1: Under the regression setting of the previous section, the following statements hold:
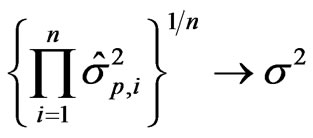
and
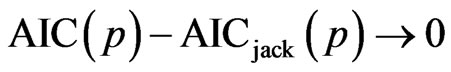
in probability as n tends to infinity.
Proof. Note that according to the jackknife methodology, the quantity 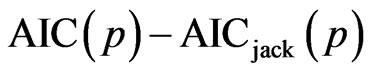 estimates the bias of the estimator:
estimates the bias of the estimator:
 .
.
Simple calculations show that
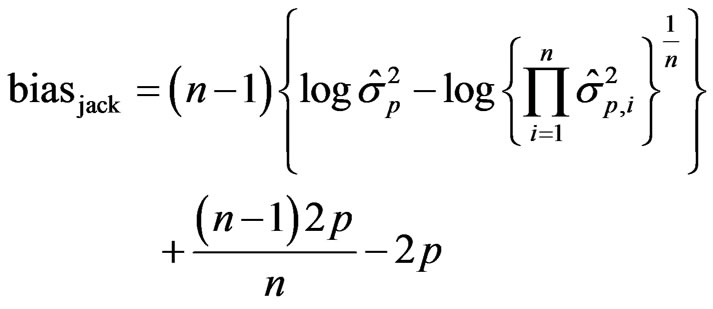
Observe that due to the consistency of the maximum likelihood estimator, we have
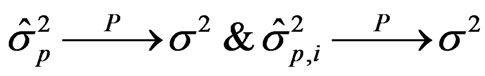
so that
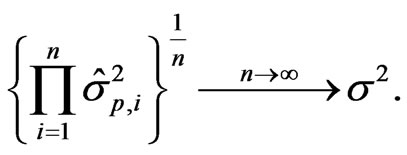
The result is immediate.
Note that the equivalence of all other variants of model selection criteria proposed in the previous Section follows immediately from the above Theorem 1. The result for BICjack and AICjack;C is provided below as a corollary without proof:
Corollary 1: Under the assumptions of Theorem 1, the following statements hold:
1) 
2) 
in probability as n tends to infinity.
Two of the main issues in model selection are consistency and asymptotic efficiency. A natural requirement for a selection procedure is to choose a model as good as possible from a given family of models. Needless to say, the goodness depends on the objective of the analysis. Consistency is our main concern whenever we know the true model as correctly as possible. In other words, the consistency is of great importance if the true model belongs to the family of models from which the selection is to be made.
The asymptotic efficiency is associated with the case where the selected model should yield a good inference. For this objective it is natural to assume that the true model does not necessarily coincide with one of the models under consideration.
It is important to point out that the two issues are not compatible. It has been shown that only the AIC – like criteria are found to be asymptotically optimal in the sense that they produce predictions with the smallest possible prediction error. At the same time these criteria have been found to be inconsistent. In particular, Shibata [7] showed that AIC tends asymptotically to overfit the true dimension (overestimation). On the other hand the BIC although not asymptotically efficient [8] it is consistent [9].
It is easy to show that the asymptotic equivalence between the AIC(.) and the proposed AICjack(.) implies that the latter is an inconsistent selection criterion. On the other hand the asymptotic efficiency is solely associated with prediction and if this is the purpose of the study, then a selection strategy carrying such a property should be used.
The issue of asymptotic efficiency was introduced by Shibata [10] and discussed by several others [6,8,11]. The main idea is based on the selection of that order (dimension) which leads to the smallest average mean squared error of prediction. The concept of asymptotic efficiency is closely associated not with an estimate of the order of the model but rather with a finite approximation to the truly infinite order of the model. Shibata was the first to make the innovative assumption that the data belong to a linear model with infinitely many parameters and established the asymptotic efficiency for zero mean autoregressive processes with Gaussian errors [10].
Recently, Lee and Karagrigoriou [12] derived a powerful result where in a time series setting the AIC-type criteria possess the asymptotic efficiency property irrespectively of the distribution of the error sequence. The main requirement for the asymptotic efficiency is the existence of the 4th moment of the error distribution. Such a result which can be easily adopted in a regression setting shows the great significance of the property. If a procedure under such minimum requirements fails to possess the asymptotic efficiency property then the criterion should not be considered appropriate for predictive purposes.
The following theorem shows the asymptotic optimality of the proposed AICjack(.) criterion.
Theorem 2: Under certain regularity assumptions, the order  selected for a p-dimensional regression model or an AR(p) process by the adjusted AICjack criterion, is asymptotically efficient, i.e., as n tends to infinity
selected for a p-dimensional regression model or an AR(p) process by the adjusted AICjack criterion, is asymptotically efficient, i.e., as n tends to infinity

in probability, where  the mean squared error of prediction of the pth order model,
the mean squared error of prediction of the pth order model,  the average mean squared error of prediction and
the average mean squared error of prediction and  the sequence that minimizes
the sequence that minimizes 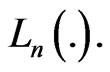
Proof. The asymptotic equivalence of AIC(p) and AICjack(p) from Theorem 1, implies that the same asymptotic result holds for any p and therefore it holds for the quantities  and
and 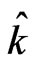 that minimize the two criteria AICjack and AIC respectively. Hence,
that minimize the two criteria AICjack and AIC respectively. Hence,
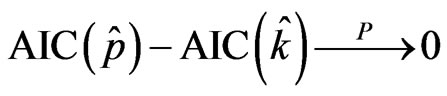 Due to the above asymptotic equivalence, the same asymptotic result holds for the mean squared error of prediction:
Due to the above asymptotic equivalence, the same asymptotic result holds for the mean squared error of prediction:
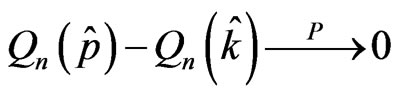
or equivalently
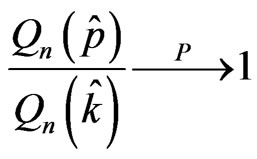 .
.
The desired result follows from:

where the first term tends to 1 by the above result and the other two by the asymptotic efficiency of the original AIC criterion (Shibata, 1980, Theorem 5.2).
3. Applications and Discussion
In this section, some small scale simulation studies are invoked. The simulations were performed with the Windows version of the Statistical Software SAS.
Small number of observations (10 - 50) is simulated for a two - independent variable standard normal regression model of the form
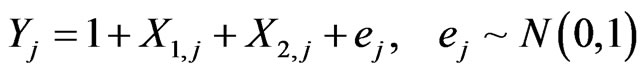 (3)
(3)
with j = 1,2, ··· ,13 where
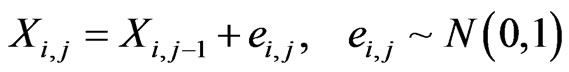
with i = 1,2,3, j = 1,2, ··· ,13 and Xi,0 = 0 for i = 1,2,3. Notice that an extra variable is available which does not enter into the true model given by Equation (3). A total of seven (7) models are available, namely the full model, 3 single-variable models and 3 two-variable models. Note finally that in what follows, the true model is the one involving the independent variables X1 and X2.
We observe that the standard criteria, AIC, BIC and AICC select the correct model in all situations. The adjusted AIC criterion, AICjack, proposed in the present work separates clearly the correct model as well as the “larger” model involving all 3 independent variables but selects the bigger one by a relatively small margin.
In this study we have also used the new adjusted criterion AICjack,C which combines the AICjack with the small sample correction term of Hurvich and Tsay ([6], see Equation (2)). The form of the criterion is given by
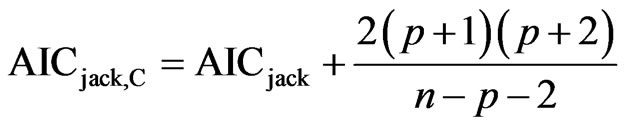 .
.
Note that in our simulation study, the resulting criterion selects the correct model. The actual values of the all the above selection criteria for all models involved are presented in Table 1.
Furthermore, the simulation study allows for the inclusion of outliers. In particular, approximately 20% of the observations in each case are dropped and replaced by observations from various Normal distributions with zero mean and variance larger than 1. In fact, the previous simulation study is repeated with the exception that the last 3 observations are replaced with 3 observations coming from a different normal distribution, namely N (0, 2). Although the standard AIC criterion selects the correct model the same is not true for BIC. Furthermore, the corrected AICC selects the correct model but the value of the criterion for the model with the single independent variable X1 stays very close.
The proposed criteria perform quite well in this case. In particular, the AICjack separates very well the correct model as well as the “larger” ones and selects with a very small margin the bigger one while the AICjack,C with a large margin selects the correct model. The results in this case are summarized in Table 2.
Similar results have been found by simulation studies performed with various samples sizes (n = 20, 30 and 50) and with two (2) additional variables that do not enter into the true model which is given by Equation (3).
All studies arrive at similar conclusions. It should be noted that the effect of the adjustment on AIC depends on the particular application. In particular, if outlying observations are present, then their contribution is downgraded since the jackknife technique reduces their impact. On the other hand, if outlying observations are not present, then the correct model as well as models “larger than” the correct one are easily recognized and the values of the adjusted AIC criteria are well separated from all other candidate models. In particular, it is shown that for any k > p0 and any 

which implies that the proposed criterion separates two competing models much more clearly than the original AIC criterion as long as the models are “larger” than the true model. It should be pointed out that the sample size n in combination with the proportion of outlying observations plays a crucial role. When we deal with relatively small sample sizes (n < 50), differences are easily observed between the proposed jackknife-based criteria and all other known criteria. As the sample size increases, the differences are less distinctive. On the other hand though, if outlying observations are present, the proposed technique can identify the phenomenon much easier than other criteria, adjust accordingly the value of the associated jackknife criteria and proceed with the correct selection. In other words, the presence of outliers makes the
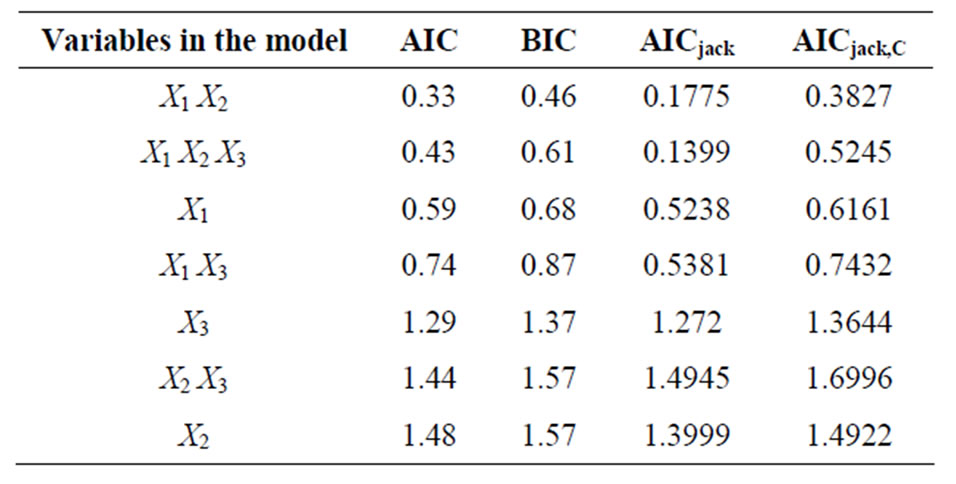
Table 1. Exact values of model selection criteria for simulated data without outliers.
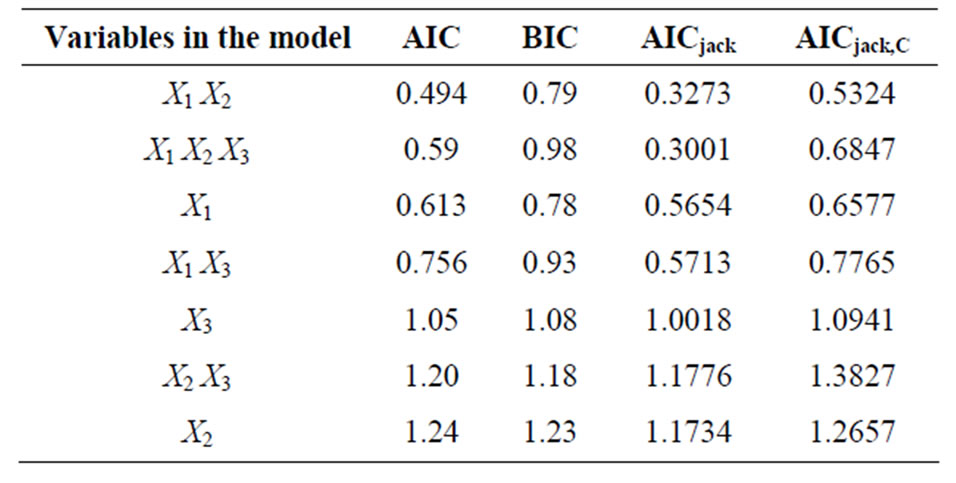
Table 2. Exact values of model selection criteria for simulated data with outliers.
proposed criteria superior to the traditional ones. If though no outliers are present, all criteria have a similar behaviour, especially for large sample sizes (n > 100). If the proportion of outliers is small and the sample size relatively large, the advantages gained by the proposed criteria is limited. The higher the proportion of outliers (combined with small to medium sample sizes), the higher the usefulness of the proposed criteria. As an anonymous referee pointed out, this special feature of our jackknife criteria may be useful in cases where mixtures of distributions are involved, an issue we intend to explore in detail in the near future.
To investigate the behavior of the proposed criteria in a real case, we use the well known Hald’s data (see [13] and [14]). This application is of great interest since different criteria select different models. The response variable represents the heat evolved in calories per gram of cement and the four covariates X1, X2, X3, X4 are measured as percent of the weight of the clinkers from which the cement was made. The AIC criterion selects the full model (all four variables) while BIC and AICC select the model with the variables X1, X2 and X4. Our jackknife criterion although chooses as the best model, the full model, gives as its second best choice the model with only two variables, namely X2 and X3. Note that these diverse results are due to the fact that there is a strong correlation between the variables X1 and X3 as well as between the variables X2 and X4. This implies that the investigator looses a relatively small amount of information if one of the variables X1 and X3 or one of the variables X2 and X4 is missing from the selected model. In that sense, the second best model selected by our jackknife selection criterion appears to be an ideal selection. The appropriateness and possible superiority of the jackknife criteria in situations with heavy correlation between covariates needs further investigation.
Applications of the proposed criteria are found in several settings among which one could mention medical data sets were outlying observations often appear. The outlier detection issue is closely related to the issue of reference (normal) range. The reference range plays the key role in determining the type and the extent of the therapeutic or pharmaceutical action to be taken. In reality the determination of a reference range is equivalent to the construction of a confidence interval in which the true value of a population characteristic lies with high probability.
Recall that the modeling, the statistical inference as well as the prediction inference may be heavily affected by the presence of outliers. The identification of the correct model for a set of data that includes outliers reduces the undesirable features of the above effect and in turn increases the reliability of the resulted confidence interval (reference range).
The so called censored linear regression models provide yet another class of models to which the proposed model selection technique could be applied. These models appear in the standard regression model setting, namely
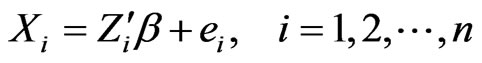
with the exception that we do not observe the event time Xi but instead the triplet (Ti, Zi, Di) which refer to three i.i.d. random variables such that Ti = mn(Xi, Ci), Ci = censored time, Zi = covariate vector and Di = 0 if Xi > Ci and 1 otherwise.
We also assume that the errors ei are independent of Zi and Ci and 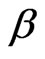 is the unknown vector of parameters. Consistent estimators can be found and the MSE of prediction as well as the Average MSE of prediction can be evaluated. The asymptotic efficiency of the standard selection criteria and the adjusted criteria proposed in this work are easily established.
is the unknown vector of parameters. Consistent estimators can be found and the MSE of prediction as well as the Average MSE of prediction can be evaluated. The asymptotic efficiency of the standard selection criteria and the adjusted criteria proposed in this work are easily established.
4. Acknowledgements
The authors would like to express their appreciation to the Editor and an anonymous referee for constructive and valuable comments that considerably improved the quality and the appearance of the manuscript.
5. References
[1] H. Akaike, “Information Theory and an Extension of the Maximum Likelihood Principle,” Proceeding of 2nd International Symposium on Information Theory, Vol. 1, No. 1973, 1973, pp. 267-281.
[2] B. Efron, “Estimating the Error Rate of a Prediction Rule: Improvement on Cross Validationn,” Journal of the American Statistical Association, Vol. 78, No. 382, 1983, pp. 316-331. doi:10.2307/2288636
[3] B. Efron and R. J. Tibshirani, “An Introduction to Bootstrap,” Chapman and Hall, New York, 1993.
[4] J. E. Cavanaugh, and R. H. Shumway, “A Bootstrap Variant of AIC for State-Space Model Selection,” Statistica Sinica, Vol. 7, No. 2, 1997, pp. 473-496.
[5] G. Schwarz, “Estimating the Dimension of a Model,” The Annals of Statistics, Vol. 6, No. 2, 1978, pp. 461-464. doi:10.1214/aos/1176344136
[6] C. M. Hurvich and C. L. Tsai, “Regression and Time Series Model Selection in Small Samples,” Biometrika, Vol. 76, No. 2, 1989, pp. 297-307. doi:10.1093/biomet/76.2.297
[7] R. Shibata, “Selection of the Order of an Autoregressive Model by Akaike’s Information Criterion,” Biometrika, Vol. 63, No. 1, 1976, pp. 117-126. doi:10.1093/biomet/63.1.117
[8] A. Karagrigoriou, “Asymptotic Efficiency of Model Selection Criteria: The Nonzero Mean Gaussian AR(Infinity) Case,” Communications in Statistics: Theory and Methods, Vol. 24, No. 4, 1995, pp. 911-930. doi:10.1080/03610929508831530
[9] C. Z. Wei, “On Predictive Least Squares Principles,” The Annals of Statistics, Vol. 20, No. 1, 1992, pp. 1-42. doi:10.1214/aos/1176348511
[10] R. Shibata, “Asymptotically Efficient Selection of the Order of the Model for Estimating Parameters of Linear Process,” The Annals of Statistics, Vol. 8, No. 1, 1980, pp. 147-164. doi:10.1214/aos/1176344897
[11] A. Karagrigoriou, “Asymptotic Efficiency of the Order Selection of a Nongaussian AR Process,” Statistica Sinica, Vol. 7, 1997, pp. 407-423.
[12] S. Lee and A. Karagrigoriou, “An Asymptotically Optimal Selection of the Order of a Linear Process,” Sankhyā: The Indian Journal of Statistics, Series A, Vol. 63, No. 1, 2001, pp. 93-106.
[13] H. Woods, H. H. Steinour and H. R. Starke, “Effect of Composition of Portland Cement on Heat Evolved during Hardening,” Industrial and Engineer Chemistry, Vol. 24, No. 11, 1932, pp. 1207-1214. doi:10.1021/ie50275a002
[14] N. Draper and H. Smith, “Applied Regression Analysis,” 2nd Edition, John Wiley, New York, 1981.

