Open Journal of Physical Chemistry
 Vol. 3  No. 1 (2013) , Article ID: 27896 , 9 pages DOI:10.4236/ojpc.2013.31008

Intense Long-Lived Fluorescence of 1,6-Diphenyl-1,3,5-Hexatriene: Emission from the S1-State Competes with Formation of O2 Contact Charge Transfer Complex

Katharina Hunger, Karl Kleinermanns*

Institute for Physical Chemistry, Heinrich-Heine-University, Düsseldorf, Germany

Email: *kleinermanns@uni-duesseldorf.de

Received October 18, 2012; revised November 20, 2012; accepted December 23, 2012

Keywords: DPH; Time-Resolved; Fluorescence; Simulations; Kinetics; Diphenylpolyenes

ABSTRACT

The fluorescence kinetics of 1,6-diphenyl-1,3,5-hexatriene (DPH) dissolved in cyclohexane was investigated as a function of temperature, concentration and 355 nm excitation pulse energy. At concentrations above 2.5 μM and excitation energies above 1 mJ a long-lived, very intense emission, which appears within less than 5 ns and lasts up to 70 ns, is observed. During the first 50 ns the decay does not follow an exponential but rather a linear behaviour. In oxygen saturated solutions the long-lived emission is suppressed and solely short-lived fluorescence with τ < 5 ns can be detected. A kinetic simulation was performed, based on a model whereupon the long-lived emission originates from the S1-state and competes with the formation of DPH-O2 contact charge-transfer complexes and intersystem crossing which both quench the fluorescence. Our investigations show that even the small amount of oxygen dissolved in nitrogen saturated solutions has a distinct influence on the fluorescence kinetics of DPH.

1. Introduction

Carotenes constitute an important molecular class for photosynthesis. They are part of the light-harvesting complex, where they absorb visible light and transfer the energy to the reaction center of the photosystem. Alltrans-α,ω-diphenylpolyenes (also referred to as minicarotenes) are well established as model compounds for the bigger carotenoids such as β-carotene or lutein [1-6]. The latter absorb light and transfer the energy to the chlorophyll unit of the pigment [7]. Another function is protection of the photosynthetic apparatus against damage by highly reactive singlet oxygen [8]. The photophysical properties of these molecules are complex and not fully understood.

Because of its strong emission 1,6-diphenyl-1,3,5- hexatriene (DPH) is used as a fluorescence probe in biological membrane systems [9]. It is known, that the measured fluorescence lifetime is longer than that calculated using the Stickler-Berg [10] relationship and that the lifetime varies with the solvent [11,12]. Hudson and Kohler found evidence that the lowest excited singlet state in diphenyloctatetraene is the 1Ag-state with the 1Bu-state lying slightly above and applied this ordering of states to other polyenes as well [12-14]. Alford and Palmer stated that DPH emission occurs from both states [15]. In the gas phase fluorescence lifetimes up to 90 ns are reported and assigned to S1-(1Ag) state emission with intensity borrowing from the S2-(1Bu) state [16].

Combined density functional theory/multi reference configuration interaction (DFT/MRCI) calculations of the low-lying singlet and triplet states of mini-β-carotenes showed that the sequence of states depends on conjugation length and nuclear geometry [17]. According to the DFT/MRCI calculations for DPH the lowest excited singlet state upon vertical excitation is the 1Bu-state, while it switches order with the 1Ag-state during geometry relaxation [18]. Equilibration of the states takes place within less than a picosecond [19,20], due to the conical intersection between the S1 and S2 potential energy hypersurfaces [18].

Emission from the S1-state is symmetry forbidden, but it can occur via mixing with the S2-state, due to the small S1-S2 energy gap [21,22]. Unlike the S1-state, the energy of the S2-state is influenced by the solvent, which leads to a solvent dependent S1-S2 energy gap and because of the state mixing to a solvent dependent S1 radiative rate [14].

Saltiel et al. presented evidence showing that the fluorescence spectrum of DPH not only consists of the combined S1/S2-emission, but also of emission from the s-cis conformers of DPH [23-27]. Catalán confirmed the influence of s-cis conformers on the emission spectra also for other minicarotenes by calculations [28,29]. A detailed resolution of the emission spectra was accomplished by Turek et al. [30].

We observe DPH emission with an exceptionally long lifetime which decays non-exponentially under special experimental conditions. The long lifetime may be due to the emission originating from a forbidden transition. But to understand the unusual temporal behaviour, additional influences have to be considered. In this work we studied the temporal fluorescence behavior under different conditions like various DPH and O2 concentrations and different temperatures and excitation laser pulse energies to identify the various competing processes like formation of DPH-O2 contact charge-transfer (CCT) complexes, whose interplay leads to the linear decay of the longlived emission.

2. Materials and Methods

1,6-Diphenyl-1,3,5-hexatriene (98%, Aldrich) and cyclohexane (99+%, Acros Organics) were used without further purification. The nanosecond transient fluorescence setup (Applied Photophysics) utilizes the output from a frequency tripled (355 nm) pulsed Nd:YAG laser (Innolas) for photoexcitation. DPH samples were excited with 0.01 - 5 mJ pump energy at 5 ns laser pulse width and 1 or 10 Hz repetition rate. The short laser pulse is created by cutting out the maximum of the 12 ns pulse with a pockels cell. The pump beam of 1 cm diameter is directed into the sample (a flow-through 3.5 mL cuvette) perpendicular to the fluorescence sampling direction. If not stated otherwise, the solution reservoir was purged with nitrogen during the experiment to remove dissolved oxygen from the solutions. The same setup was used to saturate the solutions with oxygen. The samples were purged at least for 20 minutes before the start of the first measurement. The fluorescence light is dispersed behind the sample with a grating monochromator (Applied Photophysics) for wavelength selection. The output signal is detected by a photomultiplier (R928, Hamamatsu) and digitized by an oscilloscope (Agilent Infinium). Typically 16 laser pulses are averaged to record a kinetic trace at a selected wavelength. Stationary absorption spectra were recorded with a Cary 50 (Varian) spectrometer.

The simulations of the kinetic curves were performed with Mathcad 2001 (MathSoft, Inc.) by solving the coupled nonlinear partial differential equations by numerical integration.

3. Results and Discussion

1,6-Diphenyl-1,3,5-hexatriene in cyclohexane shows strong absorption in the region of 300 - 380 nm [11, 21,31]. The excitation wavelength used for our transient fluorescence measurements (355 nm) is near to the absorption maximum of DPH at 353 nm. The emission is very intense and can be detected in solutions with DPH concentrations below 10−10 mol/L (spectra not shown here). After excitation, the fluorescence kinetics can be investigated in our setup. Figure 1 shows the fluorescence decay of an 8.0 × 10−6 M DPH solution flushed with nitrogen. The fluorescence intensity reaches its maximum within the 5 ns laser pulse and subsequently decreases linearly until 50 ns after the laser pulse, where the decay becomes monoexponential. As can be seen in the inset, a monoexponential fit does not describe the observed fluorescence decay as well as a linear fit. Linear decay kinetics are characteristic for zero order reactions which are typical for systems saturated by the reactants (no concentration change) or for processes where the minority partner is regenerated, like a catalyst. The rate constant k obtained according to the rate law is 1.85 × 107 M∙s−1.

If the same sample is flushed with oxygen, fluorescence intensity and lifetime decrease dramatically (Figure 1).

Under these conditions the fluorescence decay is best described monoexponentially, with a decay time of τ = 4.59 ns ± 0.11 ns, which corresponds to the laser pulse width. Thus, the observed decay time does represent an upper limit for the emission lifetime. The dispersed emission spectra after laser excitation of both the nitrogen and oxygen flushed samples agree with the stationary emission spectrum, except for the distortion in the region around 470 nm, where S1→Sn absorption takes place [32,33]. If the oxygen flushed sample is flushed

Figure 1. Kinetic curves of DPH (8.0 × 10−6 M) at 427 nm upon excitation at 355 nm with 1 mJ pulse energy. The sample flushed with nitrogen shows long-lived fluorescence. In the presence of oxygen intensity and lifetime of the fluorescence are decreased significantly. The decay of the nitrogen flushed sample can be seen on a larger scale in the inset with monoexponential (dashed line) and linear (dotted line) fits.

again with nitrogen, the long-lived fluorescence reappears. The decrease of fluorescence lifetime and intensity is thus not caused by oxygen induced chemical degradation of DPH but by a reversible physical process.

Both intensity and lifetime of the long-lived fluorescence increase with increasing concentration, see Figure 2. At concentrations below 1 μM the fluorescence decays exponentially. Above 1 μM the decay shows the aforementioned linear behaviour. Therefore the fluorescence lifetimes shown in Figure 2 were obtained by monoexponential ([DPH] < 1 μM) and linear ([DPH] > 1 μM) fits of the kinetic traces. Upon excitation with 0.3 mJ pulse energy the lifetime reaches a plateau at 37 ns and does not increase further with increasing concentration. At concentrations below 1 μM the number of DPH molecules within the excitation volume is smaller than the number of photons irradiating the sample (Nphoton ≈ 5.4 × 1014). The saturation plateau at ≈ 1.8 µM DPH at 0.3 mJ pulse energy can thus be explained by nearly complete photon absorption if the number of molecules exceeds the number of photons sufficiently.

A further increase of fluorescence lifetime can be

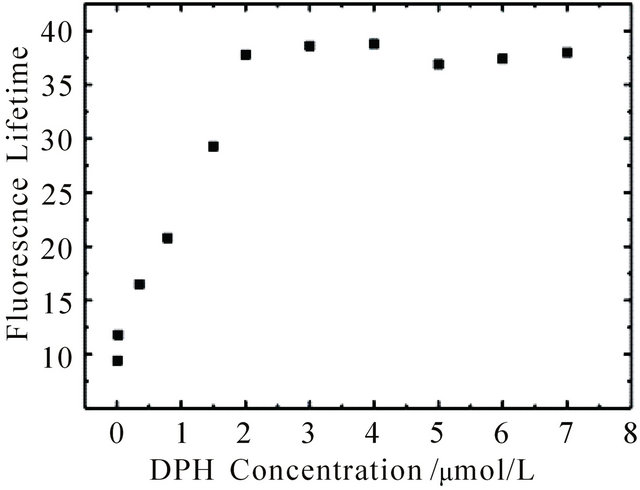
Figure 2. Fluorescence lifetime of DPH in cyclohexane at 427 nm upon excitation at 355 nm with 0.3 mJ pulse energy as a function of DPH concentration. The kinetic curves were fitted monoexponentially at concentrations below 1 mM (t given in ns) and linear above 1 mM (t given in ns∙M−1).

Figure 3. Dependence of fluorescence lifetime of DPH in cyclohexane (8.0 × 10−6 M) at 427 nm upon pumping at 355 nm on excitation laser pulse energy. For calculation of the lifetime the kinetic curves were fitted linear (t given in ns∙M−1).

reached by an increase of laser pulse energy. The effect of pulse energy on the fluorescence lifetime of an 8.0 × 10−6 M DPH solution is shown in Figure 3 between 0.01 mJ and 4 mJ. In the region of laser pulse energies below 1 mJ (Nphoton < 1.8 × 1015) the lifetime increases with increasing laser pulse energy, since the number of photons is smaller than the number of molecules (Nmolecule ≈ 2.4 × 1015). Above 1 mJ once again a plateau is reached (at 68 ns for the 8.0 × 10−6 M DPH solution). Our results thus show that fluorescence intensity and lifetime depend on the concentration of excited molecules.

The observed concentration dependence points to aggregate formation as possible cause of the long-lived fluorescence. It is well known that larger carotenoids are capable of forming aggregates easily. The emission of the aggregates is generally blue-shifted with respect to the emission of the monomer [34]. Increase of temperature leads to aggregate dissociation and a corresponding red-shift of the emission [35]. To check if the long-lived emission originates from DPH aggregates, the emission spectra of DPH were measured at different solution temperatures, spanning the complete range between melting point and boiling point of cyclohexane. The spectra at 8˚C and 75˚C are shown in Figure 4. While the shape of the kinetic traces stays unchanged (see Supplementary Material S1), it is evident that an increase of temperature leads to a decrease of fluorescence intensity. This behaviour is reversible, i.e. decreasing the temperature leads to recovery of the intensity. However, no spectral changes could be observed. Therefore, we assume that DPH does not form aggregates in cyclohexane to an appreciable extent in the concentration range of our studies. We attribute the change of intensity to an increased molecular diffusion rate at higher temperatures and therefore increased collisional quenching of the fluorescence.

The correct mechanism for generation of the longlived fluorescence has to take the following experimental findings into account: 1) fluorescence lifetimes up to ~70 ns, see Figure 1; 2) zero order decay of fluorescence intensity at short times followed by exponential decay,

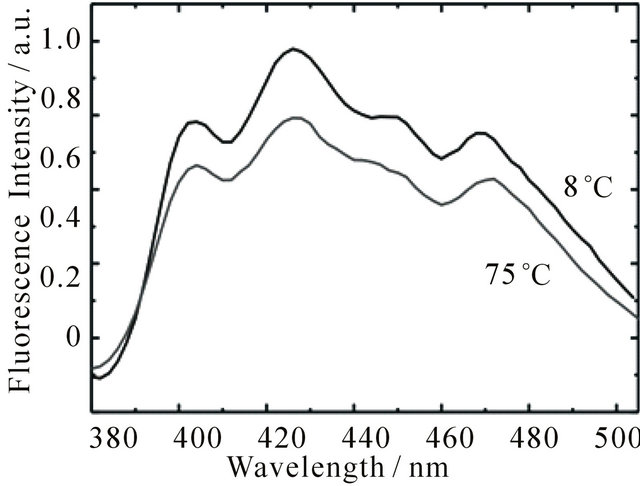
Figure 4. Emission spectra of DPH in cyclohexane (8.0 × 10−6 M) upon excitation at 355 nm with 1 mJ pulse energy at 8˚C and 75˚C. The spectra were obtained by integrating the emission during the first 30 ns after the laser pulse.

see Figure 2; 3) significant population of the DPH triplet state, because we observed intense triplet-triplet absorption (spectra not shown here, since they are well known [19,20,24,36,37]; 4) fluorescence lifetime depends on the concentration of electronically excited DPH, see Figures 2 and 3; 5) fluorescence intensity decreases with increasing temperature, see Figure 4; 6) fluorescence is quenched by higher oxygen concentrations, see Figure 1.

Different mechanisms can be discussed to explain these effects. It is known, that triplet-triplet annihilation (TTA) generates excited singlet state population with an increased fluorescence lifetime. But TTA is diffusion controlled and therefore, at the concentrations studied in this work, too slow to explain the <5 ns fluorescence risetime observed in our experiments [38]. Furthermore, the triplet ground state of DPH is very low in energy, so that the energy available by triplet-triplet annihilation is insufficient to populate the lowest excited singlet state [24,39]. Additionally, the quantum yield for intersystem crossing (ISC) of DPH is very small (i.e. 0.02 in benzene and ethanol) [40]. Nevertheless the triplet state has to be included in any model explaining the long-lived fluorescence since ISC is a competing pathway for depopulation of excited singlet states.

Ionisation, followed by electron-cation recombination to electronically excited singlet states, could also cause long fluorescence lifetimes in principle. By the recombination process, the emitting singlet state becomes populated during a certain time period, which extends the emission time. To ionize DPH (ionisation potential: 7.27 eV [41]) upon excitation with 355 nm (3.49 eV) a multiphoton process is required. The lifetime should be longer in polar solvents but very short in nonpolar solvents, since electrons are not stabilized in nonpolar solvents and recombine immediately. All experiments presented here were performed in cyclohexane, a nonpolar solvent. We did observe long-lived fluorescence in other solvents as well, but no correlation between polarity of the solvent and fluorescence lifetime was discernible from our experiments. Therefore, ionisation and recombination is not considered to be important for the emergence of long-lived DPH fluorescence.

We instead propose the mechanism displayed in Figure 5 to explain the intense long-lived DPH fluorescence. The corresponding kinetic equations, which are used to simulate the observed kinetic traces, are as follows:

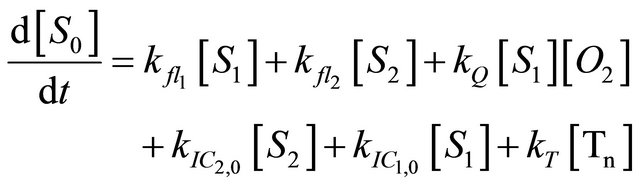(1.1)

(1.2)

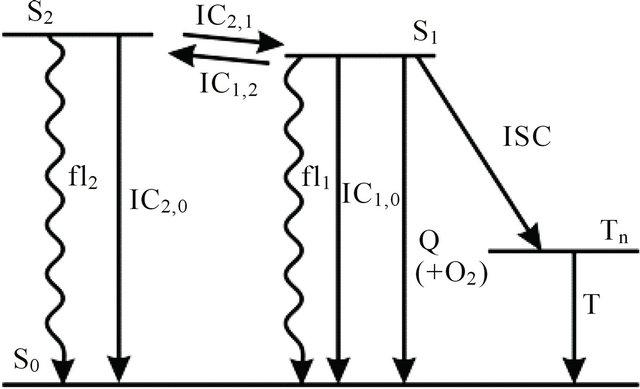
Figure 5. Proposed mechanism for emergence of long-lived fluorescence. Photoisomerization processes are not shown for clarity reasons.

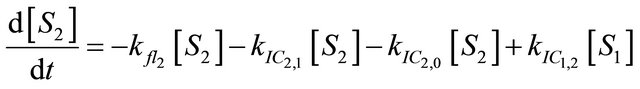(1.3)

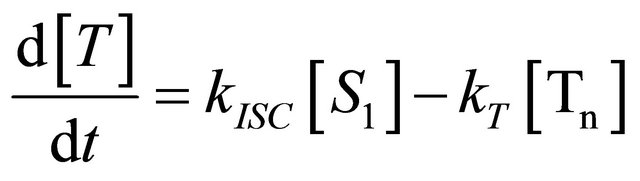(1.4)

After excitation of DPH into the S2-state a cascade of processes follows. Internal conversion into the S1-state (IC2,1) as well as the S0-state (IC2,0) occurs fast and competes with (short-lived) fluorescence (fl2) from the S2-state. The lifetime of the S1-state is affected by internal conversion into the ground state (IC1,0), reverse internal conversion into the S2-state (IC1,2) and intersystem crossing into the triplet state (ISC). Additionally, CCT complex formation with oxygen takes place. Other O2-induced processes may occur as competing processes, e.g. singulet oxygen formation or photoisomerization [42]. These processes, with the CCT complex formation as main reaction are described as oxygen quenching, (Q). In the simulation non-radiative, non-oxygen induced processes which depopulate the S1-state are indistinguishable from each other, as long as the emerging state or species has no influence on the S1-state. This includes IC1,0 and ISC as well as other possible processes, like isomerization (iso, not shown in Figure 5). Therefore it is appropriate to use a combined rate constant kdep for S1-state depopulation.

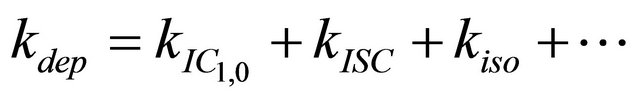(2)

IC1,2 is not included, since here the S2-state is repopulated and subsequently IC2,1 takes place, which means that the S1-state population is influenced by the state emerging from this process. Emission from the S1-state to the electronic ground state (fl1) is symmetry forbidden and should be weak, but can be promoted by intensity borrowing via S1-S2-state mixing. The triplet state is depopulated within several microseconds (T) [24].

In the following we substantiate our model. Kohler and Spiglanin observed a DPH fluorescence lifetime of 90.7 ns in the gas phase and assigned this to emission from the S1-state which borrows intensity from the nearby S2-state [16]. We follow this assignment and ascribe the long-lived fluorescence observed in our experiments to emission from the S1-state. The zero order fluorescence decay of deoxygenated DPH solutions necessitates a quencher of constant concentration. The most obvious candidate is oxygen which at high concentrations quenches the long-lived fluorescence of DPH completely. Although the solutions were purged with nitrogen continuously during the experiments to avoid quenching, a small amount of oxygen remains in the solution [43]. It is well known, that molecular oxygen forms contact complexes with hydrocarbons [43-46], whether they are unsaturated, like DPH, or saturated, like cyclohexane (CH), from which absorption to the contact charge-transfer complex (M+O2−) can take place. Strong O2/CH CCT complex absorption occurs in the region around 210 nm [43]. A deconvolution of the broad absorption band was carried out for unpurged cyclohexane as well as for nitrogen and oxygen saturated cyclohexane, and the O2-CH contact complex concentrations were determined (see Table 1) using the extinction coefficients published by Brownrigg and Kenny [43] (for a detailed description see Supplementary Material S2). The same analysis was carried out for a solution of DPH in cyclohexane. By saturating the unpurged solutions with nitrogen, the contact complex concentration is reduced by at least an order of magnitude, but the amount of remaining oxygen is still considerable ([O2 − CH] = 0.2 mM).

We assume that oxygen bound in the O2-CH complex does not contribute to quenching of the DPH fluorescence in contrast to free oxygen which is in equilibrium with the O2-CH contact complex:

(3)

To include the oxygen quenching into the simulation it

Table 1. Concentration of the contact complex [O2-M] in cyclohexane and in a DPH/cyclohexane solution (8.0∙10−6 M), calculated from deconvoluted UV/Vis absorption and the extinction coefficients published by Brownrigg and Kenny [43].

a)Complex absorption too large to determine complex concentration.

is thus necessary to estimate the amount of free oxygen contained in the solution. It is safe to assume that the equilibrium is strongly located on the side of the contact complex [46-48]. For some hydrocarbons the value of the equilibrium constant K is known to be larger than 1000 M−1. In our case this would imply a free oxygen concentration on the order of 3 × 10−8 M. This is not sufficient to effectively quench the triplet state, but formation of contact complexes between oxygen and excited DPH molecules can occur and thereby depopulate the S1-state. Ultimately, the complexes will break apart under formation of ground or triplet state DPH and free O2 [44,45]. The O2-CH complex serves as oxygen reservoir, the concentration of free oxygen [O2] therefore can be regarded as constant. Directly after the laser pulse the O2 concentration is distinctly smaller than the concentration of S1-state DPH so that the reaction rate depends on constant [O2] and nearly constant [S1] which serves as excess reservoir. This results in zero order reaction kinetics. Later on, when [S1] and [O2] are in the same order of magnitude, the reaction rate depends on the declining S1 concentration and the constant [O2] and the quenching of S1-DPH becomes a first order reaction. With these assumptions made, the kinetic trace of the DPH fluorescence was simulated by fitting the rate constants to the experimental kinetic trace of the 8.0 × 10−6 M DPH solution, excited with 1 mJ pulse energy. The value for was set to 5.0 × 104 s−1, according to the triplet state lifetimes known from literature [24,36,49,50] and [O2] to 0.03 µM according to the estimations described in Supplementary Materials S2.

The fluorescence signal detected in the experiments is composed of contributions from the S1-state and the S2-state. For comparison to the emission intensity detected during the first 100 ns after the laser pulse, the time-dependent evolution of the combined S1 + S2 population derived from the simulation is depicted in Figure 6(a) (signal intensity simulation: grey curves). The resulting set of rate constants is displayed in Table 2 together with the time constants derived thereof.

The slope of the experimental data is emulated considerably better than by a simple monoexponential fit (see inset of Figure 1). Since the concentration of free oxygen could only be estimated, it is advisable to discuss the value of [O2]∙ rather than 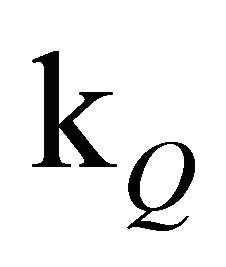alone.

Apparently, the long emission lifetime detected in our experiments derives from the S1 fluorescence, while fluorescence from the S2-state with its lifetime of 1.3 ns (Table 2) cannot be held responsible. The value for 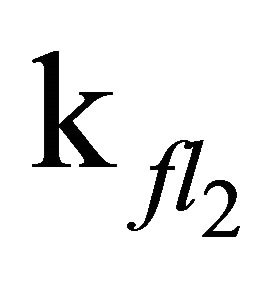obtained in our simulation corresponds well with the Einstein probability of spontaneous emission (A21 = 7.98 × 108·s−1), which can be calculated via equation 4 with the oscillator strength ƒ21 = 2.16, determined by Ye et al.: [51,52].

Table 2. Rate constants derived from the simulation of the time dependent fluorescence of DPH in cyclohexane (8.0 × 10−6 M), flushed with N2, upon excitation with 1 mJ pulse energy.

a)with free oxygen concentration [O2] = 0.03 µM.

(a)(b)

Figure 6. Time dependent fluorescence of DPH in cyclohexane at 427 nm upon excitation with 1 mJ pulse energy, flushed with N2. The grey curves show the sum of concentrations of S1 and S2-state DPH obtained from the simulations. (a) [DPH] = 8.0∙10−6 M (b) [DPH] = 2.0∙10−8 M.

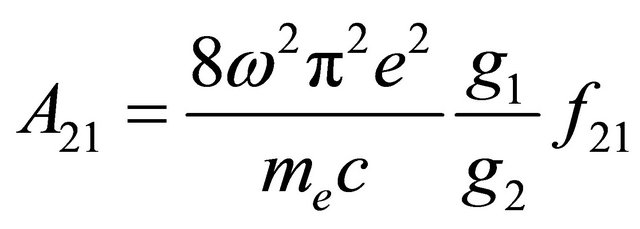(4)

Increasing the value for to the theoretical rate constant determined by Turek et al. [30] (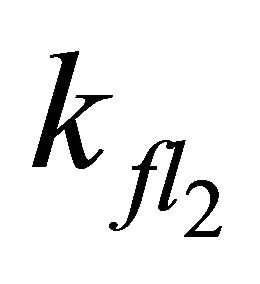= 2.2 × 109·s−1) also leads to satisfying results with the rootmean-square deviation of the simulation slightly increasing from 0.005 to 0.006.

Simulations with < 7.98 × 108 s−1 (even with = 0) describe our experimental data equally well. However, exclusion of S2-state emission influences the simulation during the first picoseconds. Without S2-state emission, an increase of emission intensity should be observed within the first 5 ps. This rise should not be observable if emission from the S2-state occurs, since S2-state emission would superimpose the S1-state emission. Since this is far beyond our experimental time resolution, we can make no substantiated statement whether S2-state emission occurs in DPH or not.

In simulations with larger or smaller 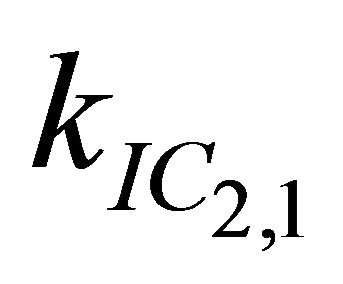combined with smaller emission occurs from the S2-state with a long lifetime but the decay is strictly exponential rather than showing the described linear behaviour during the first 50 ns. The linearity can only be obtained by including the O2 quenching as competing process to S1 fluorescence.

The simulation starting value for was set to 1.6 × 1012 s−1, which is the value corresponding to the S2-state lifetimes obtained by Hirata et al. [20], but a better agreement with our experimental data was obtained with = 7.3 × 1011 s−1. Decreasing 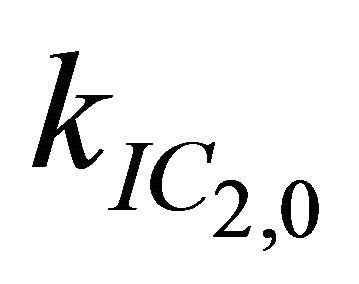to values below 1.0 × 1010 s-1 has no effect on the simulation at all, while higher values for this rate lead to insufficient simulations. Therefore 1.0 × 1010 s−1 is only an upper bound for.

It was found that the fluorescence intensity decreases with increasing temperature, while the shape of the kinetic trace stayed unchanged. The emission intensity strongly depends on the S2-state concentration. At higher temperatures, depopulation of the S2-state by collisional quenching increases. Since this process competes with IC2,1, the S1-state is populated less at higher than at lower temperatures. This results in a decrease of emission intensity. Apparently, collisional quenching plays a minor role in S1-state depopulation.

With an adjusted initial [S2] the same rate constants can also be used to describe the fluorescence of DPH solutions at much lower concentrations, as is shown in Figure 6(b) for [DPH] = 2.0 × 10−8 M. In this case [S1] is already smaller than [O2] directly after the laser pulse. The fluorescence decay is therefore exponential, in the experiment as well as in the simulation. The emission in oxygen saturated solutions resembles the shape of the laser pulse with its lifetime of 5 ns, see Figure 1. In oxygen saturated solutions [O2] is much higher than the initial concentration of excited state DPH. This leads to a very fast O2-quenching of the S1-state in our simulations, which results in a fluorescence decay within 1 ns. Due to our 5 ns laser pulse it is not possible in our setup to measure the correct fluorescence lifetime of the oxygen saturated sample.

4. Conclusion

At high pulse energies of the excitation laser the singlet emission of 1,6-diphenyl-1,3,5-hexatriene can occur via two different pathways. On the one hand, after excitation to the S2-state, emission occurs directly from the pumped state. On the other hand, IC into the S1-state takes place. The fluorescence from the S1-state features long lifetimes since it is symmetry forbidden and can only occur by intensity borrowing via state mixing with the S2-state. The S1-state is depopulated by several processes like reverse IC, ISC and fluorescence. Most important competing process is the formation of DPH-O2 contact complexes, which at low oxygen concentrations considerably influences the kinetic trace of the long-lived fluorescence and quenches the long-lived fluorescence considerably at high oxygen concentrations.

5. Acknowledgements

The authors thank the Deutsche Forschungsgemeinschaft (KL 531/29-1) for financial support and Prof. Weinkauf for valuable discussions.

REFERENCES

  1. S. M. Bachilo, C. W. Spangler, and T. Gillbro, “Excited State Energies and Internal Conversion in Diphenylpolyenes: from Diphenylbutadiene to Diphenyltetradecaheptaene,” Chemical Physics Letters, Vol. 283, No. 3-4, 1998, pp. 235-242. doi:10.1016/S0009-2614(97)01373-0
  2. P. O. Andersson, et al., “Dual Singlet State Emission in a Series of Mini-Carotenes,” Journal of Luminescence, Vol. 51, No. 1-3, 1992, pp. 11-20. doi:10.1016/0022-2313(92)90014-Z
  3. R. L. Christensen, et al., “S1 and S2 States of Apoand Diapocarotenes,” The Journal of Physical Chemistry A, Vol. 103, No. 14, 1999, pp. 2399-2407.
  4. W. Mizukami, et al., “Ab initio Study of the Excited Singlet States of All-trans α,ω-Diphenylpolyenes with One to Seven Polyene Souble Bonds: Simulation of the Spectral Data within Franck-Condon Approximation,” Journal of Chemical Physics, Vol. 131, No. 17, 2009, pp. 10. doi:10.1063/1.3261729
  5. T. Polivka and V. Sundstrom, “Dark Excited States of Carotenoids: Consensus and Controversy,” Chemical Physics Letters, Vol. 477, No. 1-3, 2009, pp. 1-11. doi:10.1016/j.cplett.2009.06.011
  6. M. Yoshizawa, et al., “Ultrafast Relaxation Kinetics of Excited States in a Series of Miniand Macro-β-Carotenes,” Physical Review B, Vol. 67, No. 17, 2003, p. 8.
  7. H. A. Frank, et al., “Carotenoid-to-Bacteriochlorophyll Singlet Energy Transfer in Carotenoid-Incorporated B850 Light-Harvesting Complexes of Rhodobacter sphaeroides R-26.1,” Photochemistry and Photobiology, Vol. 57, No. 1, 1993, pp. 49-55. doi:10.1111/j.1751-1097.1993.tb02254.x
  8. M. Ricci, et al., “Internal Conversion and Energy Transfer Dynamics of Spheroidene in Solution and in the LH-1 and LH-2 Light-Harvesting Complexes,” Chemical Physics Letters, Vol. 259, No. 3-4, 1996, pp. 381-390. doi:10.1016/0009-2614(96)00832-9
  9. S. Yamashita, A. G. Szabo and P. Cavatorta, “Temperature Dependence and Decay Kinetics of the High-Energy Band in DPH Fluorescence,” Bulletin of the Chemical Society of Japan , Vol. 62, No. 9, 1989, pp. 2849-2853. doi:10.1246/bcsj.62.2849
  10. S. J. Strickler and R. A. Berg, “Relationship between Absorption Intensity and Fluorescence Lifetime of Molecules,” The Journal of Physical Chemistry, Vol. 37, No. 4, 1962, pp. 814-822. doi:10.1063/1.1733166
  11. E. D. Cehelnik, et al., “1,6-Diphenyl-1,3,5-hexatriene as a Fluorescence Standard,” Chemical Physics Letters, Vol. 27, No. 4, 1974, pp. 586-588. doi:10.1016/0009-2614(74)80311-8
  12. B. Hudson and B. Kohler, “Linear Polyene Electronic Structure and Spectroscopy,” Annual Review of Physical Chemistry, Vol. 25, No. 1974, pp. 437-460. doi:10.1146/annurev.pc.25.100174.002253
  13. B. S. Hudson and B. E. Kohler, “A Low-Lying Weak Transition in the Polyene α,ω-Diphenyloctatetraene,” Chemical Physics Letters, Vol. 14, No. 3, 1972, pp. 299- 304.
  14. B. S. Hudson and B. E. Kohler, “Polyene Spectroscopy: The Lowest Energy Excited Singlet State of Diphenyloctateratene and Other Linear Polyenes,” The Journal of Physical Chemistry, Vol. 59, No. 9, 1973, pp. 4984-5002. doi:10.1063/1.1680717
  15. P. C. Alford and T. F. Palmer, “Photophysics of Derivatives of all-trans-1,6-Diphenyl-1,3,5-hexatriene (DPH); Part 1.—Model involving Fluorescence from S2 and S1 Excited States,” Journal of the Chemical Society, Faraday Transactions 2, Vol. 79, No. 1983, pp. 433-447. doi:10.1039/f29837900433
  16. B. E. Kohler and T. A. Spiglanin, “Structure and Dynamics of Excited Singlet States of Isolated Diphenylhexatriene,” The Journal of Physical Chemistry, Vol. 80, No. 11, 1984, pp. 5465-5471. doi:10.1063/1.446655
  17. M. Kleinschmidt, et al., “Parallel Multireference Configuration Interaction Calculations on Mini-β-Carotenes and β-Carotene,” The Journal of Physical Chemistry, Vol. 130, No. 4, 2009, pp. 044708. doi:10.1063/1.3062842
  18. B. Küpper, et al., “On the Photophysics of 1,6-Diphenyl- 1,3,5-Hexatriene Isomers and Rotamers,” ChemPhysChem, Vol. 12, No. 10, 2011, pp. 1872-1879. doi:10.1002/cphc.201001068
  19. W. A. Yee, et al., “Femtosecond Transient Absorption Studies of Diphenylpolyenes. Direct Detection of S2→S1 Radiationless Conversion in Diphenylhexatriene and Diphenyloctatetraene,” Chemical Physics Letters, Vol. 276, No. 5-6, 1997, pp. 430-434. doi:10.1016/S0009-2614(97)00842-7
  20. Y. Hirata, et al., “Energy Gap Dependence of the S2→S1 Internal Conversion of α,ω-Diphenylpolyenes (N=3-8) in Solution Phase,” Chemical Physics Letters, Vol. 308, No. 3-4, 1999, pp. 176-180.
  21. S. M. Bachilo, E. V. Bachilo and T. Gillbro, “Spectral Shape of Diphenylpolyene Fluorescence and Mixing of the S1 and S2 States,” Chemical Physics, Vol. 229, No. 1, 1998, pp. 75-91.
  22. T. Itoh, “Evidence for the Coexistence of Two Different Mechanisms for the Occurrence of Anti-Kasha S2 (11Bu) Fluorescence from α,ω-Diphenylpolyenes,” The Journal of Physical Chemistry, Vol. 121, No. 14, 2004, pp. 6956- 6960.
  23. J. Saltiel, et al., “Evidence for Ground-State S-Cis Conformers in the Fluorescence Spectra of All-trans-1,6-diphenyl-1,3,5-hexatriene,” Journal of the American Chemical Society, Vol. 114, No. 10, 1992, pp. 3607-3612. doi:10.1021/ja00036a004
  24. J. Saltiel, et al., “Cis-Trans Photoisomerization of the 1,6-Diphenyl-1,3,5-hexatrienes in the Triplet State. The Quantum Chain Mechanism and the Structure of the Triplet State,” The Journal of Physical Chemistry A, Vol. 102, No. 28, 1998, pp. 5383-5392. doi:10.1021/jp972941c
  25. J. Saltiel, et al., “Direct Photoisomerization of the 1,6-Diphenyl-1,3,5-hexatrienes. Medium Effect on Triplet and Singlet Contributions,” The Journal of Physical Chemistry A, Vol. 104, No. 48, 2000, pp. 11443-11450. doi:10.1021/jp002359f
  26. J. Saltiel, et al., “Photoisomerization of All-trans-1,6-Diphenyl-1,3,5-hexatriene. Temperature and Deuterium Isotope Effects,” The Journal of Physical Chemistry A, Vol. 107, No. 18, 2003, pp. 3178-3186. doi:10.1021/jp021540g
  27. J. Saltiel, et al., “Photoisomerization of All-cis-1,6-Diphenyl-1,3,5-hexatriene in the Solid State and in Solution: A Simultaneous Three-Bond Twist Process,” Angewandte Chemie International Edition, Vol. 48, No. 43, 2009, pp. 8082-8085. doi:10.1002/anie.200902724
  28. J. Catalan and J. L. G. de Paz, “On the Photophysics of All-trans-Polyenes: Hexatriene versus Octatetraene,” The Journal of Physical Chemistry, Vol. 124, No. 3, 2006, pp. 034306-11. doi:10.1063/1.2158992
  29. J. Catalan, “The Emission of α,ω-Diphenylpolyenes: A Model Involving Several Molecular Structures,” Chem. Phys., Vol. 335, No. 1, 2007, pp. 69-78. doi:10.1016/j.chemphys.2007.03.023
  30. A. M. Turek, et al., “Resolution of Three Fluorescence Components in the Spectra of All-trans-1,6-Diphenyl- 1,3,5-hexatriene under Isopolarizability Conditions,” The Journal of Physical Chemistry A, Vol. 109, No. 2, 2005, pp. 293-303. doi:10.1021/jp045201u
  31. M. T. Allen and D. G. Whitten, “The Photophysics and Photochemistry of α,ω-Diphenylpolyene Singlet States,” Chem. Rev., Vol. 89, No. 8, 1989, pp. 1691-1702.
  32. J. C. del Valle, N. Tarkalanov, and J. Saltiel, “Distortion of the Fluorescence Spectrum of All-trans-1,6-Diphenyl-1,3,5-hexatriene with Increasing Laser Pulse Excitation Energies,” The Journal of Physical Chemistry B, Vol. 103, No. 43, 1999, pp. 9350-9355. doi:10.1021/jp991450k
  33. C. M. Marian and N. Gilka, “Performance of the Density Functional Theory/Multireference Configuration Interaction Method on Electronic Excitation of Extended pSystems,” Journal of Chemical Theory and Computation, Vol. 4, No. 9, 2008, pp. 1501-1515. doi:10.1021/ct8001738
  34. A. Hager, “Ausbildung von Maxima im Absorptionsspektrum von Carotinoiden im Bereich um 370 nm; Folgen für die Interpretation Bestimmter Wirkungsspektren,” Planta, Vol. 91, No. 1, 1970, pp. 38-53. doi:10.1007/BF00390164
  35. A. V. Ruban, P. Horton, and A. J. Young, “Aggregation of Higher Plant Xanthophylls: Differences in Absorption Spectra and in the Dependency on Solvent Polarity,” Journal of Photochemistry and Photobiology B, Vol. 21, No. 2-3, 1993, pp. 229-234. doi:10.1016/1011-1344(93)80188-F
  36. S. K. Chattopadhyay, P. K. Das, and G. L. Hug, “Photoprocesses in Diphenylpolyenes. Oxygen and Heavy-Atom Enhancement of Triplet Yields,” Journal of the American Chemical Society, Vol. 104, No. 17, 1982, pp. 4507-4514. doi:10.1021/ja00381a001
  37. Z. Wang and W. G. McGimpsey, “Time-Resolved Evidence for Isomerization of Diphenylpolyene Cation Radicals in Solution,” The Journal of Physical Chemistry, Vol. 97, No. 13, 1993, pp. 3324-3327. doi:10.1021/j100115a038
  38. J. Saltiel and B. W. Atwater, “Spin-Statistical Factors in Diffusion-Controlled Reactions”, In: D. H. Volman, G.S. Hammond and K. Gollnick, Eds., Advances in Photochemistry, John Wiley & Sons, Inc., New York 1988, pp. 63-76.
  39. J. Saltiel, J. M. Crowder and S. Wang, “Mapping the Potential Energy Surfaces of the 1,6-Diphenyl-1,3,5-hexatriene Ground and Triplet States,” Journal of the American Chemical Society, Vol. 121, No. 5, 1999, pp. 895- 902. doi:10.1021/ja982551j
  40. R. Bensasson, et al., “The Triplet State of 1,6-Diphenyl- 1,3,5-hexatriene and 1,8-Diphenyl-1,3,5,7-octatetraene,” Chemical Physics Letters, Vol. 41, No. 2, 1976, pp. 333- 335. doi:10.1016/0009-2614(76)80823-8
  41. M. Klessinger and E. Gunkel, “The Electronic Structure of Polyenes and Unsaturated Carbonyl Compounds,” Tetrahedron, Vol. 34, No. 24, 1978, pp. 3591-3598. doi:10.1016/0040-4020(78)88436-1
  42. K. C. Wu and A. M. Trozzolo, “Production of Singlet Molecular-Oxygen from the Oxygen Quenching of the Lowest Excited Singlet-State of Aromatic Molecules in n-Hexane Solution,” The Journal of Physical Chemistry, Vol. 83, No. 24, 1979, pp. 3180-3183. doi:10.1021/j100487a023
  43. J. T. Brownrigg and J. E. Kenny, “Fluorescence Intensities and Lifetimes of Aromatic Hydrocarbons in Cyclohexane Solution: Evidence of Contact Charge-Transfer Interactions with Oxygen,” The Journal of Physical Chemistry A, Vol. 113, No. 6, 2009, pp. 1049-1059. doi:10.1021/jp807495h
  44. R. Schmidt, “Photosensitized Generation of Singlet Oxygen,” Photochemistry and Photobiology, Vol. 82, No. 5, 2006, pp. 1161-1177. doi:10.1562/2006-03-03-IR-833
  45. C. Schweitzer and R. Schmidt, “Physical Mechanisms of Generation and Deactivation of Singlet Oxygen,” Chem. Rev., Vol. 103, No. 5, 2003, pp. 1685-1757. doi:10.1021/cr010371d
  46. E. A. Gooding, K. R. Serak and P. R. Ogilby, “GroundState Benzene-Oxygen Complex,” The Journal of Physical Chemistry, Vol. 95, No. 20, 1991, pp. 7868-7871. doi:10.1021/j100173a058
  47. K. Kikuchi, et al., “New Aspects on Fluorescence Quenching by Molecular Oxygen,” Journal of the American Chemical Society, Vol. 115, No. 12, 1993, pp. 5180-5184. doi:10.1021/ja00065a033
  48. L. Rodríguez, et al., “Photophysical Study of Naphthalenophanes: Evidence of Adduct Formation with Molecular Oxygen,” The Journal of Physical Chemistry A, Vol. 115, No. 2, 2011, pp. 123-127. doi:10.1021/jp106887c
  49. T. Kamisuki and C. Hirose, “Photoionization Mechanism of α, ω-Diphenylpolyenes in Polar Solvents Investigated by Using Coherent Raman Spectroscopy,” Journal of Photochemistry and Photobiology A, Vol. 99, No. 1, 1996, pp. 13-21. doi:10.1016/1010-6030(96)04384-5
  50. S. Nath, D. K. Palit and A. V. Sapre, “Photoinduced Charge Transfer Interaction Between Fullerene and Diphenylpolyenes in Solution: Evidence for Photocycloaddition Reaction,” Chemical Physics Letters, Vol. 330, No. 3-4, 2000, pp. 255-261. doi:10.1016/S0009-2614(00)01070-8
  51. J. F. Ye, et al., “Excess Polarizabilities upon Excitation from the Ground State to the first Dipole-Allowed Excited State of Diphenylpolyenes,” Int. J. Quant. Chem., Vol. 107, No. 10, 2007, pp. 2006-2014.
  52. J. G. Calvert and J. N. Pitts Jr., “Photochemistry,” 2nd Edition, John Wiley & Sons, Inc., New York, 1966.

Supplementary Material 1

Figure S1: Kinetic curves of DPH (8.0 × 10−6 M in cyclohexane flushed with nitrogen) at 25˚C and 75˚C upon excitation at 355 nm with 1 mJ pulse energy. The emission intensity decreases with increasing temperature, while the shape of the kinetic curves does not depend on the temperature.

Supplementary Material 2

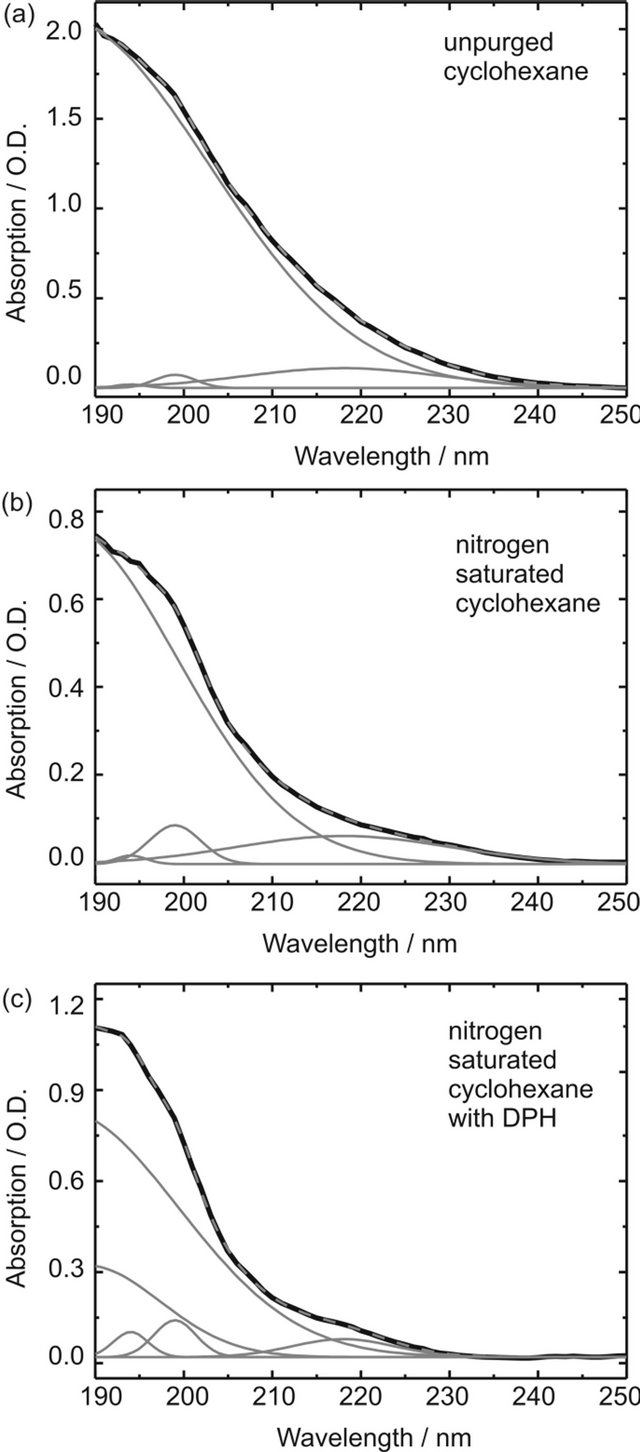
Figure S2. Absorption spectra and Gauss deconvolutions of the O2-CCT complex absorption in (a) unpurged cyclohexane; (b) cyclohexane saturated with nitrogen; (c) DPH in cyclohexane (8.0 × 10-6 M) purged with nitrogen. The experimental absorbance spectrum is depicted in black, the sum of the Gaussian curves in dashed grey (nearly perfect overlap with the black curve) and the individual Gaussian contributions in grey.

The intense curves with maxima <190 nm depend on O2 concentration and can thus be described to absorption of O2-M CCT complexes. In pure cyclohexane, neither purged with nitrogen or oxygen, the CCT absorption band can be emulated by one Gaussian curve with λmax = 186 nm and three distinctly smaller Gaussian curves with maxima at 199 nm, 194 nm and 218 nm. Unfortunately, it is not possible to investigate absorption bands below 190 nm with our UV/Vis spectrometer; hence λmax ≈ 186 nm is merely a guess. The sample was purged with nitrogen for 15 minutes and an absorption spectrum was measured every minute. Only the intensity of the Gaussian curve with λmax ≈ 186 nm had to be adjusted to emulate the spectra, while all other contributing curves remained unchanged. Therefore we assign this band to the O2-cyclohexane CCT complex absorption. The other bands are due to cyclohexane absorption and will be disregarded when calculating the contact complex concentration. Obviously the oscillator strengths of the CCT complex bands are much higher than those of uncomplexed cyclohexane in the displayed spectral range.

After seven minutes the sample was saturated with nitrogen and no changes could be observed in the absorption spectra any more. The measured CCT-absorption of the sample purged with oxygen for 15 minutes at 210 nm lies well beyond 1 O.D. where the Lambert-Beer law is not valid any more. For this sample no concentration could be determined. The concentration was calculated using the CCT extinction coefficients determined by Brownrigg and Kenny in the region of the red flank of the 186 nm band: ε210nm = 250 L∙mol−1∙cm−2, ε220nm = 120 L∙mol−1∙cm−2 and ε230nm =40 L∙mol−1∙cm−2 and the corresponding intensities obtained by our deconvolution. The concentrations given in table 1 in the article are obtained by averaging over the values for the different wavelengths.

The same analysis was performed for an 8.0 × 10−6 M DPH solution in cyclohexane. In this case not only the oxygen saturated but also the unpurged solution features an absorption band with intensities above 1 O.D. For the nitrogen saturated solution an additional Gaussian band with λmax = 189 nm was needed to emulate the CCT complex absorption, which may be due to formation of the O2-DPH CCT complex. Therefore, the summarized intensities of the Gaussian curves with λmax = 186 nm and λmax = 189 nm were used to calculate the combined contact complex concentration. It was assumed that the different CCT complexes exhibit comparable extinction coefficients.

NOTES

*Corresponding author.

Journal Menu >>