Open Journal of Discrete Mathematics
Vol.3 No.3(2013), Article ID:34513,4 pages DOI:10.4236/ojdm.2013.33027
Counting the Number of Squares Reachable in k Knight’s Moves
School of Mathematical Sciences, Rochester Institute of Technology, Rochester, USA
Email: amm2838@alum.rit.edu, DLFSMA@rit.edu
Copyright © 2013 Amanda M. Miller, David L. Farnsworth. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 30, 2013; revised May 31, 2013; accepted June 15, 2013
Keywords: Counting; Knight’s Moves; Infinite Chessboard; Geometric Argument
ABSTRACT
Using geometric techniques, formulas for the number of squares that require k moves in order to be reached by a sole knight from its initial position on an infinite chessboard are derived. The number of squares reachable in exactly k moves are 1, 8, 32, 68, and 96 for k = 0, 1, 2, 3, and 4, respectively, and 28k – 20 for k ≥ 5. The cumulative number of squares reachable in k or fever moves are 1, 9, 41, and 109 for k = 0, 1, 2, and 3, respectively, and 14k2 – 6k + 5 for k ≥ 4. Although these formulas are known, the proofs that are presented are new and more mathematically accessible then preceding proofs.
1. Introduction
Besides the game of chess, applications of knight’s moves include creating magic squares [1,2, pp. 53-63], recognizing patterns [3], identifying chemically similar elements in the periodic table [4,5, pp. 272-275, 325], and digital distance measurement [3,6,7].
We obtain formulas for the number of squares reachable by a knight on an infinite chessboard in a minimum of k moves and for the cumulative number of squares that the knight can reach in k moves. Our arguments are mainly geometric and have the advantage of being relatively elementary. These formulas are known, but our proofs are new and more mathematically accessible then currently available proofs, which are referenced in Section 3.
The knight moves in a way that is much different from the other chess pieces. A valid move is two squares left, right, up, or down, followed by one square in a direction perpendicular to the two squares. The eight squares that are available in one move to the knight K are indicated with 1s in Figure 1. Coordinates can be imposed on the infinite chessboard. Let r be the row coordinate and c be the column coordinate of the squares. The coordinates are integers. Each knight’s move consists of adding or subtracting 2 from one coordinate and adding or subtracting 1 from the other coordinate. The knight is initially at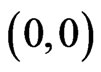 .
.
By coloring the squares alternatively white and black, starting with black in , parity arguments can be made, since a knight always moves to a square of a color different from the color of the square upon which it resides. For a knight initially at
, parity arguments can be made, since a knight always moves to a square of a color different from the color of the square upon which it resides. For a knight initially at , if r + c is even, then the square is black and the square’s value of k is even. If r + c is odd, then the square is white and the square’s value of k is odd.
, if r + c is even, then the square is black and the square’s value of k is even. If r + c is odd, then the square is white and the square’s value of k is odd.
Figure 2 contains rows and columns –12 to 12 of the infinite chessboard. The entries are the minimum number of knight’s moves that are required by the knight K to reach each square. The numbers were obtained by counting and are easily checked. In addition to the symmetries with respect to row 0 and to column 0, the two main diagonals are lines of symmetry on the whole board. The shading of the squares in Figure 2 is used in Section 2.
2. Number of Squares Requiring k Moves
We prove the following theorem.

Figure 1. A 9 ´ 9 portion of a chessboard, showing the location of a knight, K, and the eight squares that K can reach in one move.
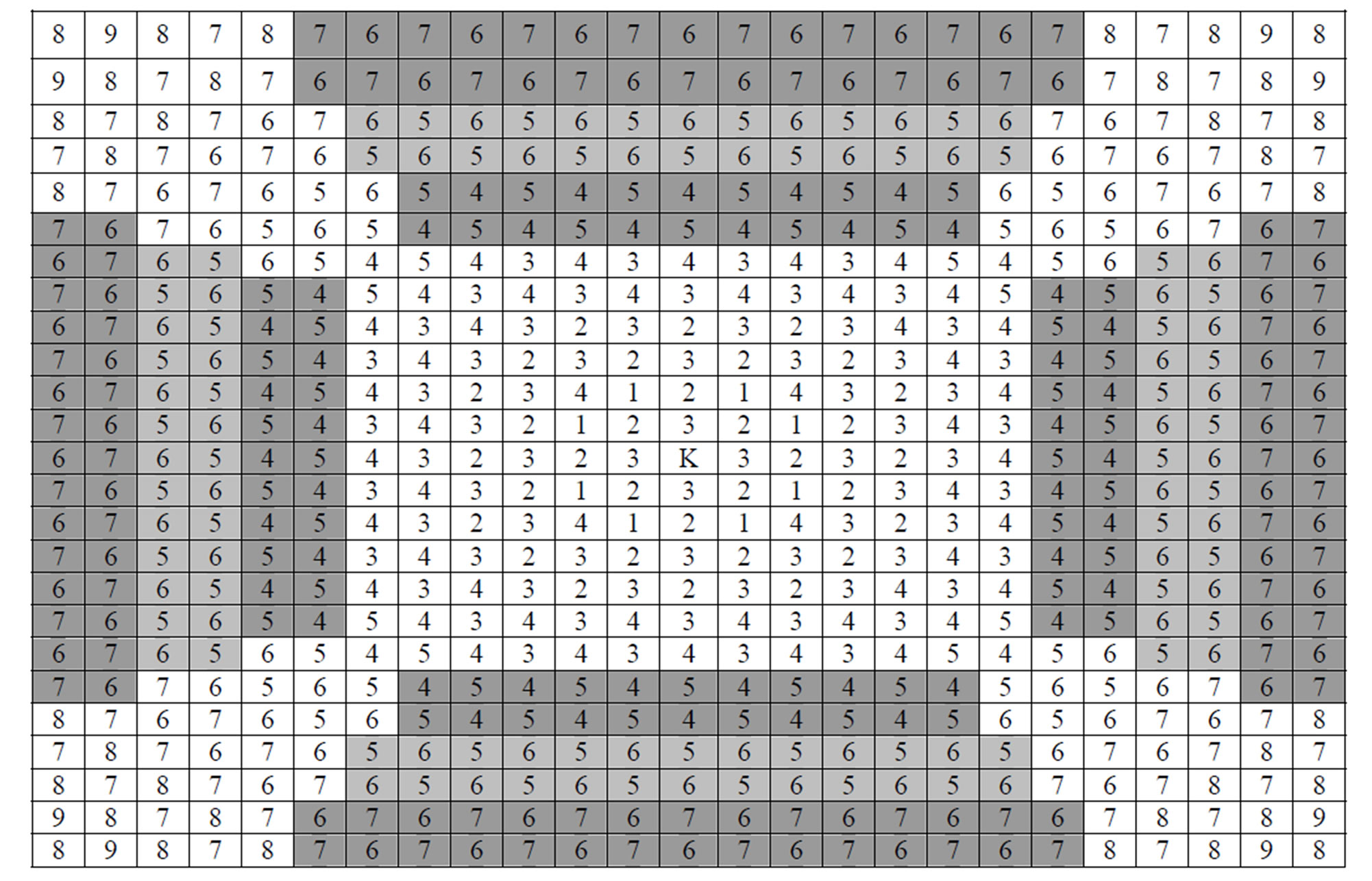
Figure 2. Rows and columns −12 to 12 of the infinite chessboard with the number of moves required in order to reach each square.
Theorem: The number of squares that require exactly k moves in order to be reached by a sole knight from its initial position on an infinite chessboard are 1, 8, 32, 68, and 96 for k = 0, 1, 2, 3, and 4, respectively, and 28k – 20 for k ≥ 5.
Proof: For k = 0, 1, 2, 3, 4, and 5, the number of squares requiring k knight’s moves from square 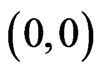 are 1, 8, 32, 68, 96, and 120, respectively. The initial 1 is for no move, so that the knight remains at (0,0). These numbers can be obtained by counting (see Figure 2).
are 1, 8, 32, 68, 96, and 120, respectively. The initial 1 is for no move, so that the knight remains at (0,0). These numbers can be obtained by counting (see Figure 2).
In order to count the number of squares for k ≥ 6, our strategy is to begin with the squares that are five moves from 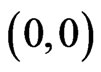 and determine which squares require six moves. The squares that require seven moves, then eight moves, and so forth can be determined similarly.
and determine which squares require six moves. The squares that require seven moves, then eight moves, and so forth can be determined similarly.
We take advantage of another symmetry, which is apparent from Figure 2. For k ≥ 5, the plane can be decomposed into eight regions of two types, I and II, using lines with slopes approximately ±2 and ±1/2. These slopes reflect the knight’s move of two squares followed by one square in the same general direction, such as, for example, always going first two east, then one north or south. These lines are used solely for reference. For simplicity, the nomenclature of compass directions is used.
The four Type I regions are to the north, west, south, and east of 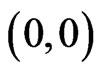 and consist of rectangles, which are two rows or two columns wide. In one move, a knight can land on only a square in an adjacent rectangle. The four Type I regions are the same up to rotations of 90˚. Figure 3 shows a portion of the eastern Type I region.
and consist of rectangles, which are two rows or two columns wide. In one move, a knight can land on only a square in an adjacent rectangle. The four Type I regions are the same up to rotations of 90˚. Figure 3 shows a portion of the eastern Type I region.
The four Type II regions are to the northeast, northwest, southwest, and southeast of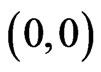 . The four Type II regions are the same up to rotations of 90˚. Figure 4 shows a portion of the northeastern Type II region. In one move, a knight can land on only a square in an adjacent shaded section.
. The four Type II regions are the same up to rotations of 90˚. Figure 4 shows a portion of the northeastern Type II region. In one move, a knight can land on only a square in an adjacent shaded section.
Consider the eastern Type I region. Consulting Figure 3, the 5 s appear in two of the rectangles’ four columns. Columns 7 and 8 have only k = 4 and k = 5, and columns 9 and 10 have only k = 5 and k = 6. There are 13 squares with k = 6 in columns 9 and 10 that are reachable in one knight’s move from the 11 squares with k = 5 in columns 7 and 8. Similarly, there are 15 squares with k = 6 in columns 11 and 12 that are reachable in one knight’s move from the 13 squares with k = 5 in columns 9 and 10. These 11 + 13 = 24 squares have 13 + 15 = 28 successor squares with k = 6. Because the rectangles increase in size by four squares and half of the additional squares are white and half are black, the 28 squares labeled 6 have 15 + 17 = 32 successor squares with k = 7 in four columns, and so forth. Since increasing k by 1 increases the count of reachable squares by 4 and the count for k = 5 is 24, the number of squares in this region that are k moves from 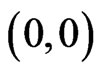 is 24 + 4(k – 5) = 4k + 4 for k ≥ 5 by an easy induction.
is 24 + 4(k – 5) = 4k + 4 for k ≥ 5 by an easy induction.
Consider the northeastern Type II region. The pattern is made more evident by turning Figure 4 clockwise 45˚, so that the squares appear to be in columns. Beginning with the six squares labeled k = 5 in three columns, there are (3) (3) = 9 successor squares with k = 6 in three col-
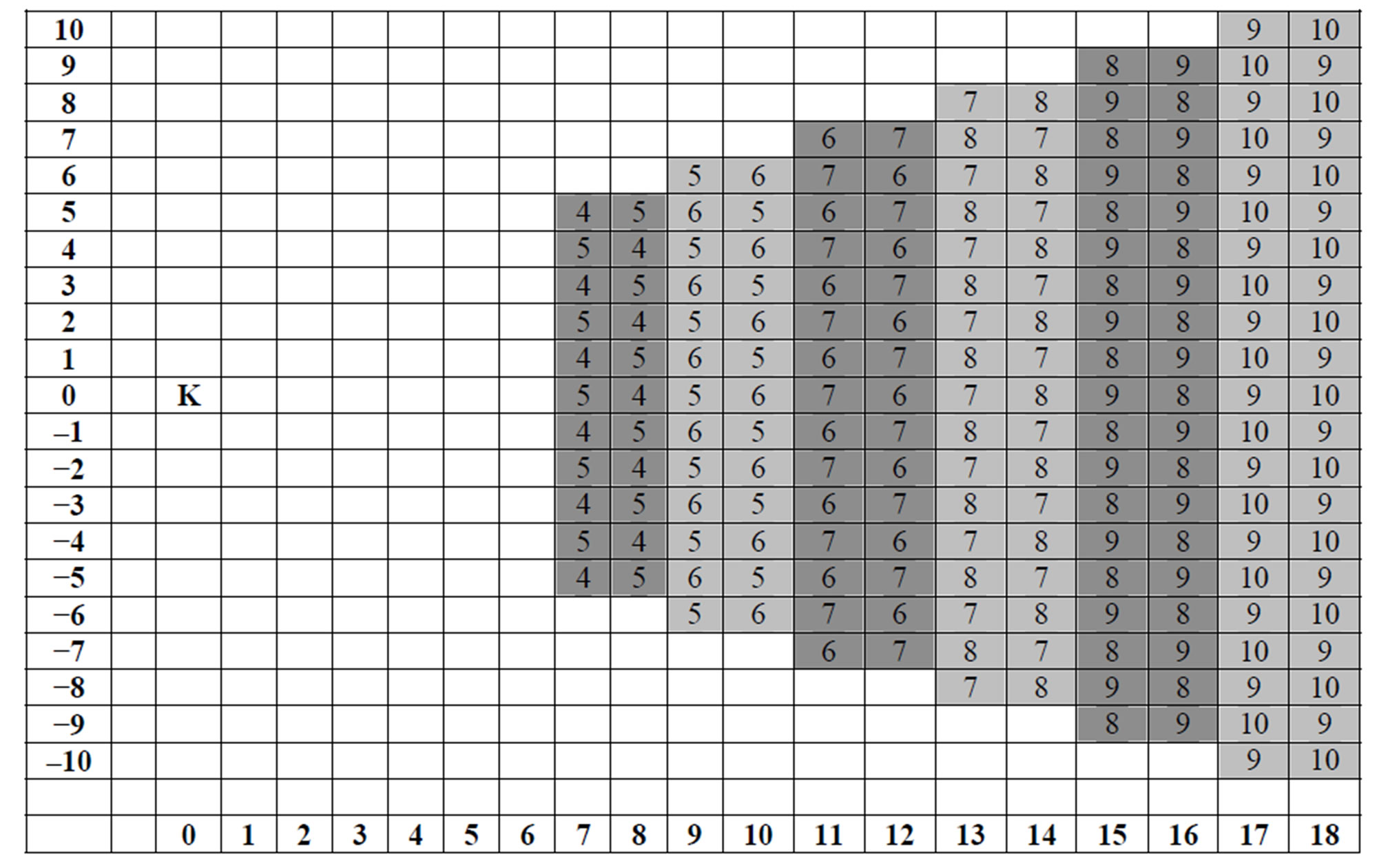
Figure 3. The first six rectangular sections of the eastern region of Type I with required counts in the squares.
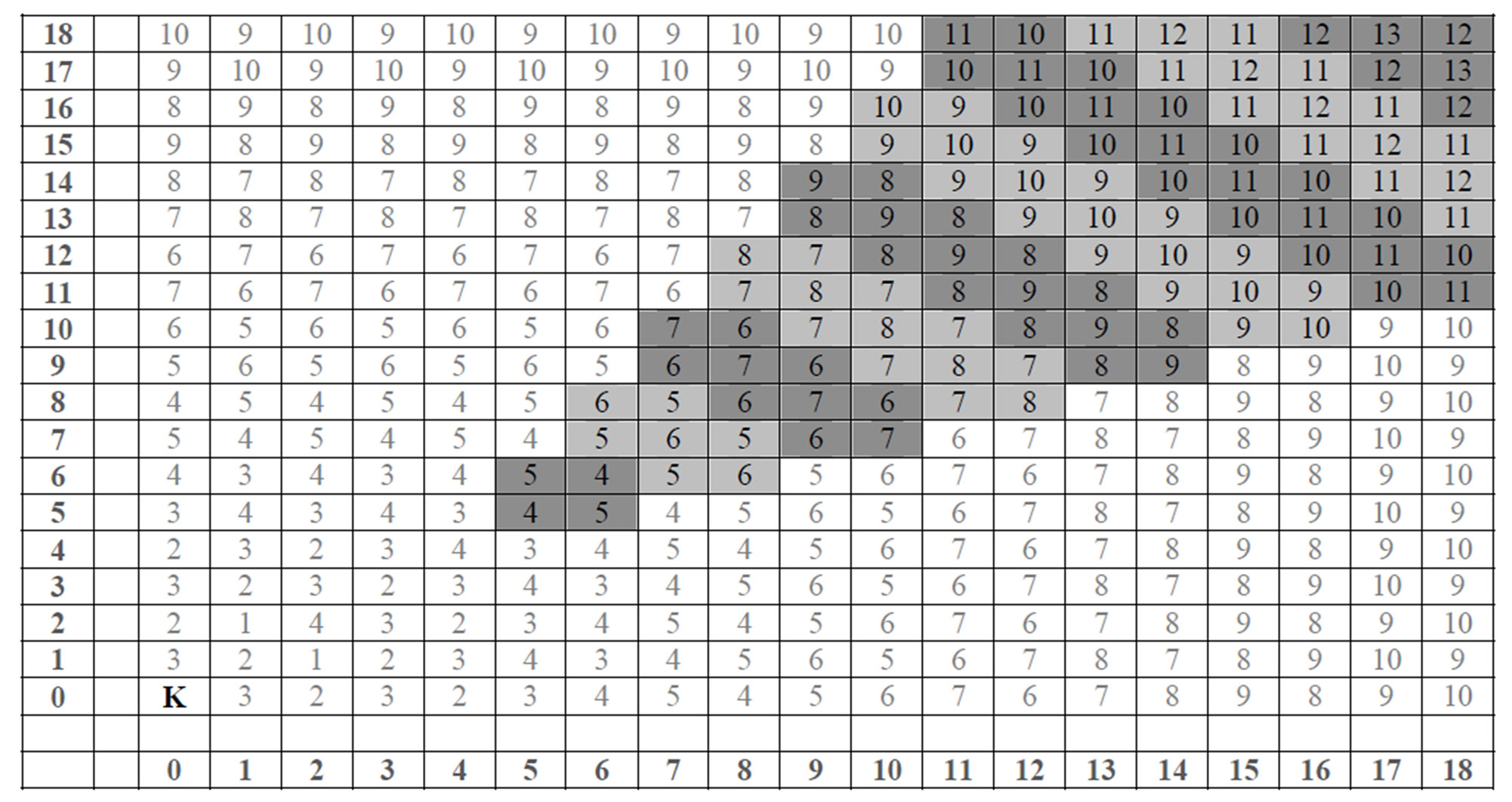
Figure 4. The northeastern region of Type II.
umns, and then there are (3) (4) = 12 successor squares with k = 7 in three columns. Since the size of each of the three columns increases by 1 in each subsequent shaded sector, there are 3(k – 3) squares that would be labeled k.
Since there are four regions of each type, the total number of squares that are a minimum of exactly k moves from 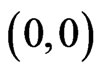 is
is 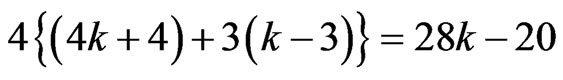 for k ≥ 5. □
for k ≥ 5. □
Simple algebra gives the following corollary.
Corollary: The cumulative number of squares reachable in k or fewer moves by a sole knight from its initial position on an infinite chessboard are 1, 9, 41, and 109, for k = 0, 1, 2, and 3, respectively, and 14k2 – 6k + 5, for k ≥ 4.
3. Other Approaches
Katzman [8] finds these formulas using Hilbert functions to count sets of monomials. Das and Chatterji [3] show that knight’s moves create a metric and subsequently give these counts. The sequence 1, 8, 32, 68, 96, 120, 148, 176, ···, which is the number of squares reachable in 0, 1, 2, ··· moves is number A018842 of the Online Encyclopedia of Integer Sequences [9]. OEIS’s sequence A018836 is the partial sums of sequence A018842. OEIS references some of Katzman’s work as its source. A simulation or computer code can be implemented to solve this and similar problems.
REFERENCES
- B. A. Balof and J. J. Watkins, “Knight’s Tours and Magic Squares,” Congressus Numerantium, Vol. 120, No. 1, 1996, pp. 23-32.
- J. J. Watkins, “Across the Board: The Mathematics of Chessboard Problems,” Princeton University Press, Princeton, 2004.
- P. P. Das and B. N. Chatterji, “Knight’s Distance in Digital Geometry,” Pattern Recognition Letters, Vol. 7, No. 4, 1988, pp. 215-226. doi:10.1016/0167-8655(88)90105-5
- W. M. Hexana and N. J. Coville, “Indium as a Chemical Promoter in Fe-Based Fischer-Tropsch Synthesis,” Applied Catalysis A: General, Vol. 377, No. 1, 2010, pp. 150- 157. doi:10.1016/j.apcata.2010.01.031
- E. R. Scerri, “The Periodic Table: Its Story and Its Significance,” Oxford University Press, Oxford, 2007.
- P. P. Das, “An Algorithm for Computing the Number of the Minimal Paths in Digital Images,” Pattern Recognition Letters, Vol. 9, No. 2, 1989, pp. 107-116. doi:10.1016/0167-8655(89)90043-3
- J. Mukherjee, P. P. Das, M. Aswatha Kumar and B. N. Chatterji, “On Approximating Euclidean Metrics by Digital Distances in 2D and 3D,” Pattern Recognition Letters, Vol. 21, No. 6-7, 2000, pp. 573-582. doi:10.1016/S0167-8655(00)00022-2
- M. Katzman, “Counting Monomials,” Journal Algebraic Combinatorics, Vol. 22, No. 3, 2005, pp. 331-341. doi:10.1007/s10801-005-4531-6
- N. J. A. Sloane, “On-Line Encyclopedia of Integer Sequences,” 2013. http://www.oeis.org

