Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27383,4 pages DOI:10.4236/ojdm.2013.31008
On Cubic Nonsymmetric Cayley Graphs*
1School of Mathematics and Statistics, Yunnan University, Kunming, China
2School of Mathematics and Information Sciences, Guangxi University, Nanning, China
Email: #lijjhx@163.com
Received October 8, 2012; revised November 8, 2012; accepted November 20, 2012
Keywords: Cubic Cayley Graph; Nonsymmetric; Non-Normal
ABSTRACT
Let  be a connected Cayley graph of group G, then Γ is called normal if the right regular representation of G is a normal subgroup of
be a connected Cayley graph of group G, then Γ is called normal if the right regular representation of G is a normal subgroup of , the full automorphism group of Γ. For the case where G is a finite nonabelian simple group and Γ is symmetric cubic Cayley graph, Caiheng Li and Shangjin Xu proved that Γ is normal with only two exceptions. Since then, the normality of nonsymmetric cubic Cayley graph of nonabelian simple group aroused strong interest of people. So far such graphs which have been known are all normal. Then people conjecture that all of such graphs are either normal or the Cayley subset consists of involutions. In this paper we give an negative answer by two counterexamples. As far as we know these are the first examples for the non-normal cubic nonsymmetric Cayley graphs of finite nonabelian simple groups.
, the full automorphism group of Γ. For the case where G is a finite nonabelian simple group and Γ is symmetric cubic Cayley graph, Caiheng Li and Shangjin Xu proved that Γ is normal with only two exceptions. Since then, the normality of nonsymmetric cubic Cayley graph of nonabelian simple group aroused strong interest of people. So far such graphs which have been known are all normal. Then people conjecture that all of such graphs are either normal or the Cayley subset consists of involutions. In this paper we give an negative answer by two counterexamples. As far as we know these are the first examples for the non-normal cubic nonsymmetric Cayley graphs of finite nonabelian simple groups.
1. Introduction
All graphs in this paper are assumed to be finite, simple, connected and undirected.
Let 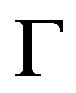 be a graph and denote
be a graph and denote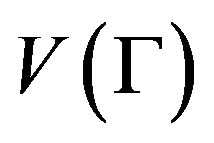 ,
, 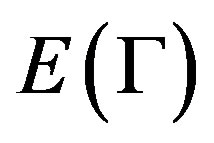 ,
,  and
and  the vertex set, edge set, arc set and full automorphism group respectively. Denote
the vertex set, edge set, arc set and full automorphism group respectively. Denote 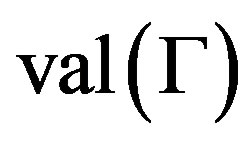 the valency of
the valency of . Then
. Then 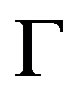 is said to be X-vertex-transitive, Xedge-transitive and X-arc-transitive if
is said to be X-vertex-transitive, Xedge-transitive and X-arc-transitive if 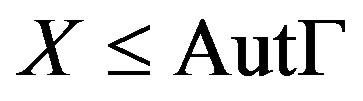 acts transitively on
acts transitively on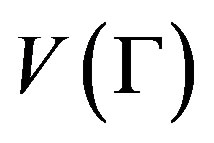 ,
, 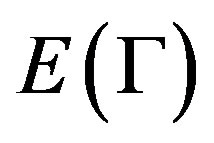 , and
, and 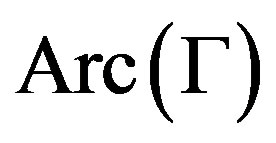 respectively. And further
respectively. And further  is simply called vertex-transitive, edgetransitive and arc-transitive when
is simply called vertex-transitive, edgetransitive and arc-transitive when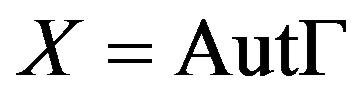 . Sometimes arc-transitive graph is simply called symmetric graph.
. Sometimes arc-transitive graph is simply called symmetric graph.
A graph 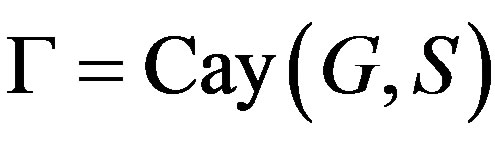 is a Cayley graph of a group
is a Cayley graph of a group  if there is a subset
if there is a subset 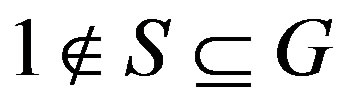 with
with
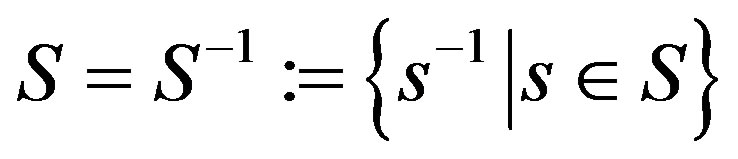 such that
such that 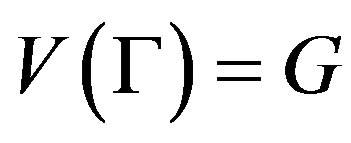 and
and
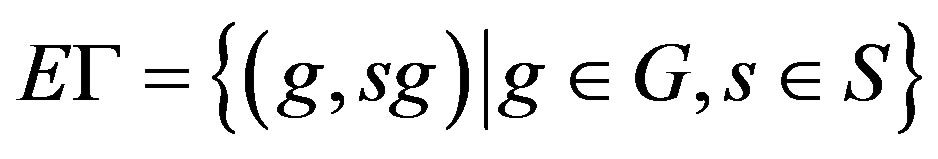 .
.
Bydefinition,  has valency
has valency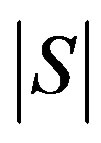 , and it is connected if and only if
, and it is connected if and only if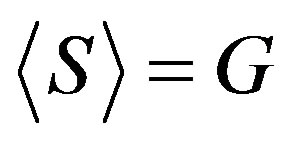 . Moreover,
. Moreover, 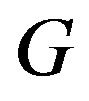 can be viewed as a regular subgroup of
can be viewed as a regular subgroup of  by right multiplication action on V(G). For convenience, we still denote this regular subgroup by G. Then a Cayley graph is vertextransitive. On the contrary a vertex-transitive graph
by right multiplication action on V(G). For convenience, we still denote this regular subgroup by G. Then a Cayley graph is vertextransitive. On the contrary a vertex-transitive graph 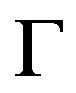 is a Cayley graph of a group G if and only if
is a Cayley graph of a group G if and only if  contains a subgroup that is regular on
contains a subgroup that is regular on 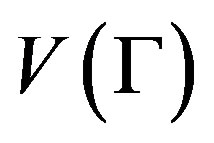 and isomorphic to G (see [1, Proposition 16.3]). If G is a normal subgroup of
and isomorphic to G (see [1, Proposition 16.3]). If G is a normal subgroup of , then
, then  is called a normal Cayley graph of G. The
is called a normal Cayley graph of G. The 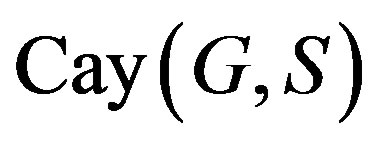 is said to be core-free (with respect to G) if G is core-free in some
is said to be core-free (with respect to G) if G is core-free in some
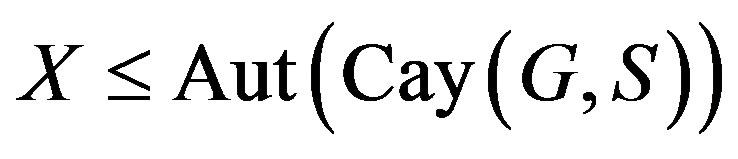 that is,
that is,
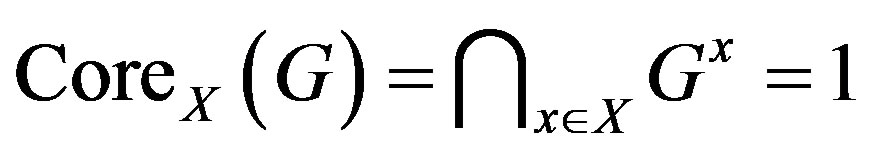 .
.
Let X be an arbitrary finite group with a core-free subgroup H and let D be a union of several double cosets of  satisfying
satisfying . The coset graph
. The coset graph  is the graph with vertex set
is the graph with vertex set
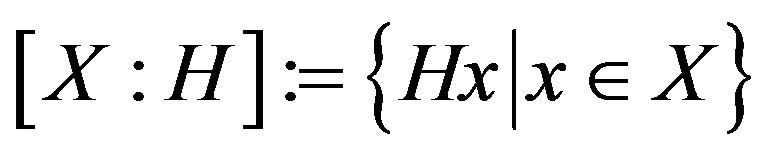
such that 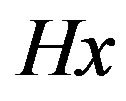 and
and 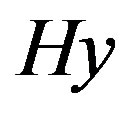 are adjacent if and only if
are adjacent if and only if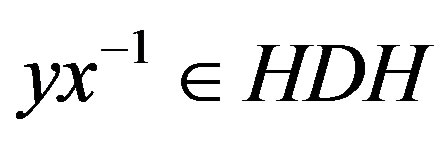 . Consider the action of X on
. Consider the action of X on 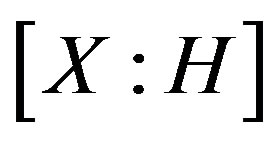 by right multiplication on right cosets. Note this action is faithful and preserves the adjacency of the coset graph, thus we identify X with a subgroup of
by right multiplication on right cosets. Note this action is faithful and preserves the adjacency of the coset graph, thus we identify X with a subgroup of . Obviously,
. Obviously, 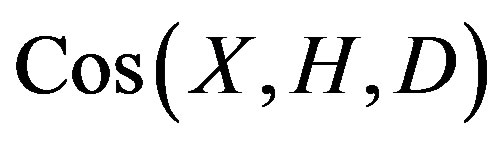 is connected if and only if
is connected if and only if . The valency of
. The valency of 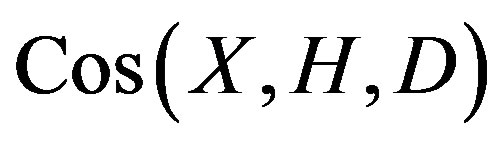 is
is . Let
. Let 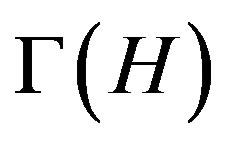 be the set of vertices of
be the set of vertices of , which are adjacent with H. It is easy to check that H has n orbits on
, which are adjacent with H. It is easy to check that H has n orbits on 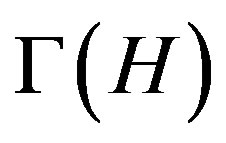 if and only if D is the union of n double cosets of H. Further, the properties stated in the following lemma are well-known, its proof can be found in [2-4].
if and only if D is the union of n double cosets of H. Further, the properties stated in the following lemma are well-known, its proof can be found in [2-4].
Proposition 1.1 Let 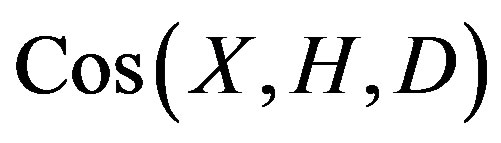 be defined as above.
be defined as above.
1) If 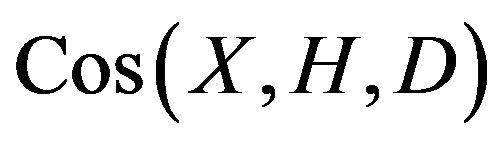 is a X-symmetric graph of valency at least 3, then there exists an element
is a X-symmetric graph of valency at least 3, then there exists an element 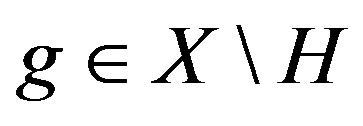 satisfying
satisfying 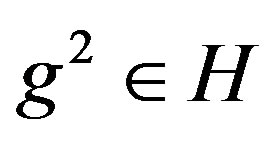 and
and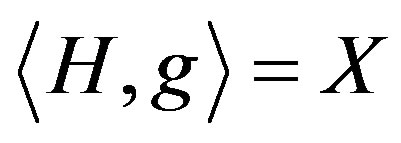 . Furthermore, we may choose g to be a 2-element;
. Furthermore, we may choose g to be a 2-element;
2) Let 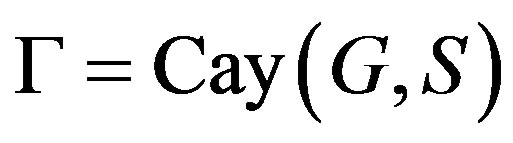 be a Cayley graph and
be a Cayley graph and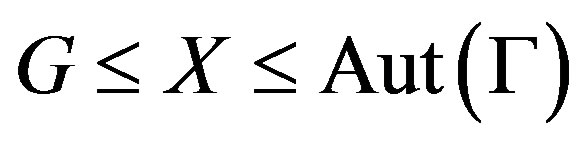 . Let
. Let 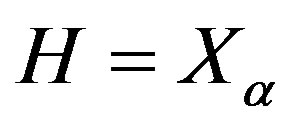 be the stabilizer of
be the stabilizer of 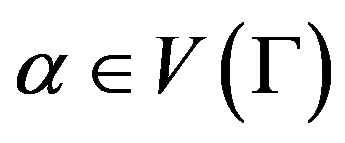 in X. We have
in X. We have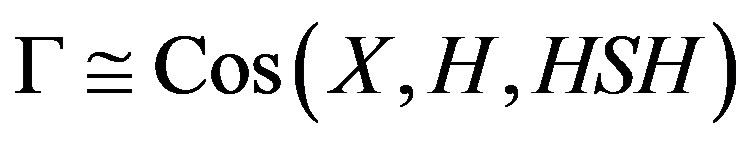 ;
;
3) Let 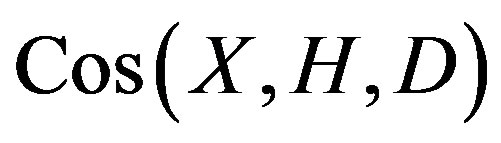 be a coset graph and G be a complement of H in X. Denote
be a coset graph and G be a complement of H in X. Denote . Then the Cayley graph
. Then the Cayley graph 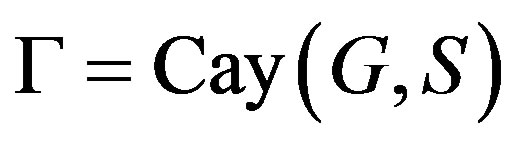 is isomorphic to
is isomorphic to
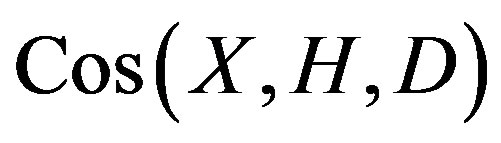 , and hence
, and hence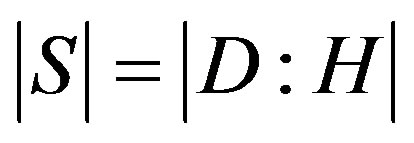 . In particular, S contains an involution of G if the valency of
. In particular, S contains an involution of G if the valency of  is odd.
is odd.
Tutte [5,6] proved that every finite connected cubic symmetric graph is 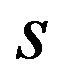 -regular for some
-regular for some . Since Tutte’s seminal work, the study of s-arc-transitive graphs, aiming at constructing and characterizing such graphs, has received considerable attention in the literature, see [7-12] for example, and now there is an extensive body of knowledge on such graphs. Fang, Li, Wang and Xu [13] proved that for most finite nonabelian simple groups, the corresponding connected cubic Cayley graphs are normal. Caiheng Li [14] and Shangjin Xu [15] proved that every cubic symmetric Cayley graph of finite nonabelian simple group is normal except two 5-arc transitive graphs of the alternating group
. Since Tutte’s seminal work, the study of s-arc-transitive graphs, aiming at constructing and characterizing such graphs, has received considerable attention in the literature, see [7-12] for example, and now there is an extensive body of knowledge on such graphs. Fang, Li, Wang and Xu [13] proved that for most finite nonabelian simple groups, the corresponding connected cubic Cayley graphs are normal. Caiheng Li [14] and Shangjin Xu [15] proved that every cubic symmetric Cayley graph of finite nonabelian simple group is normal except two 5-arc transitive graphs of the alternating group 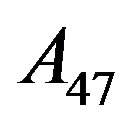 (up to isomorphic). Then it arises a natural problem: whether each of the cubic non-symmetric Cayley graph of finite nonabelian simple group is normal? This problem has become the topics of greatest concern after the results of Li and Xu. Based on past experience, people conjure that if there exist some normal graphs, then the Cayley subsets of them must be consist of involutions. However, there have no any answer to the problem until now.
(up to isomorphic). Then it arises a natural problem: whether each of the cubic non-symmetric Cayley graph of finite nonabelian simple group is normal? This problem has become the topics of greatest concern after the results of Li and Xu. Based on past experience, people conjure that if there exist some normal graphs, then the Cayley subsets of them must be consist of involutions. However, there have no any answer to the problem until now.
To answer this problem, by studying cubic nonsymmetric Cayley graphs, we give a negative answer. In the present paper, we give two non-normal examples which subsets are not consist of involutions. It’s worth noting that these are the first examples for the non-normal cubic nonsymmetric Cayley graphs of finite nonabelian simple groups.
In the rest of this section, we assume that
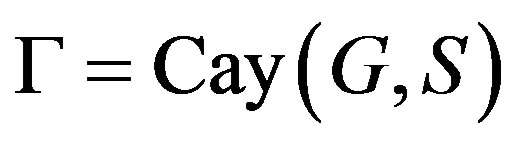 is a cubic nonsymmetric Cayley graph with
is a cubic nonsymmetric Cayley graph with . Denote H the vertex stabilizer of X on
. Denote H the vertex stabilizer of X on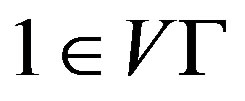 . Note
. Note 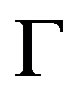 is cubic nonsymmetric, then H must be 2-group. Let N be the maximal one among normal subgroups of X contained in G, that is,
is cubic nonsymmetric, then H must be 2-group. Let N be the maximal one among normal subgroups of X contained in G, that is, 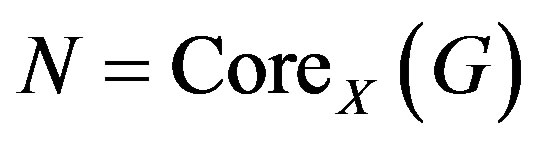 is the core of G in X.
is the core of G in X.
2. Main Results
In this section, we construct some examples of cubic nonnormal nonsymmetric Cayley graphs on finite nonableian simple groups.
Example 2.1 Let  be the alternating group A15 and set
be the alternating group A15 and set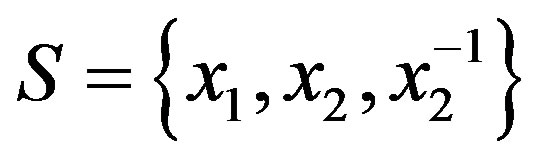 , where
, where
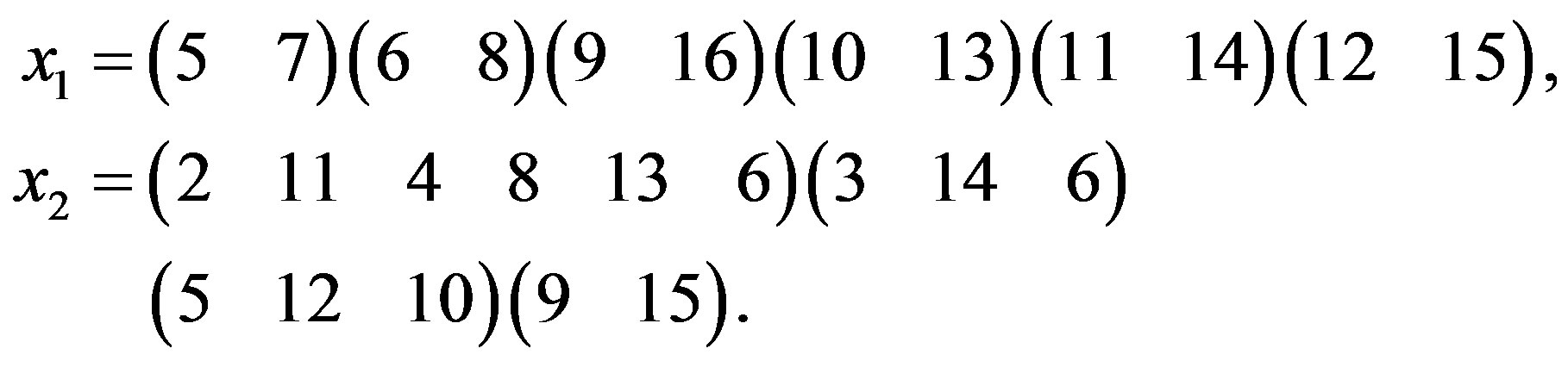
Let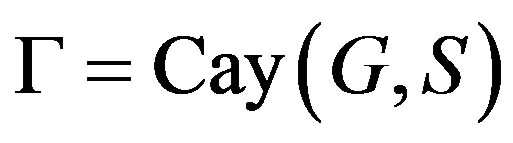 , then
, then 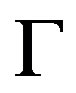 is cubic nonsymmetric connected Cayley graph, which is not normal.
is cubic nonsymmetric connected Cayley graph, which is not normal.
Let 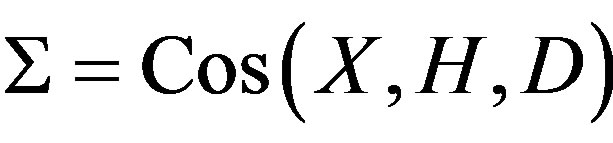 be a connected graph, where
be a connected graph, where
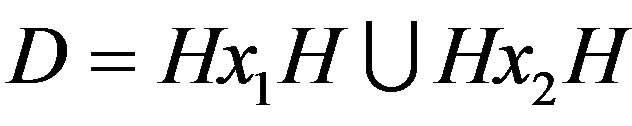 and
and 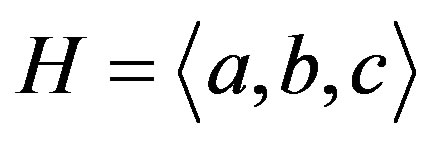 with
with

It is easy to see 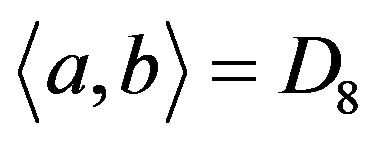 with 1 and 5 being in different orbits, which follows
with 1 and 5 being in different orbits, which follows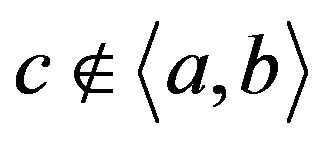 . On the other hand,
. On the other hand, 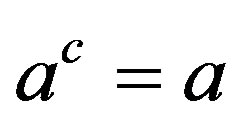 and
and 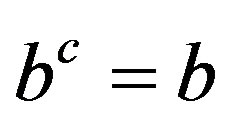 lead to
lead to
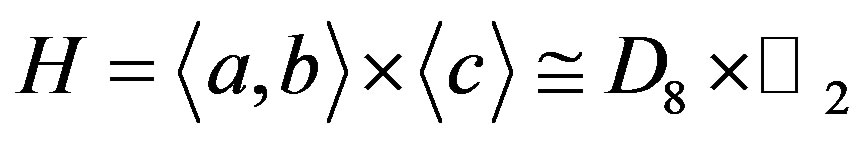 .
.
Simple computation shows  and
and  , i.e.,
, i.e., . Then the valency of
. Then the valency of 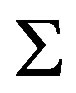 is
is , and moreover
, and moreover 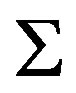 is nonsymmetric since
is nonsymmetric since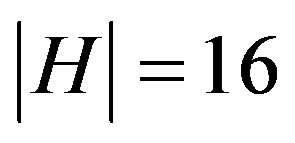 . Since
. Since 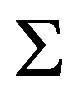 is connected, so
is connected, so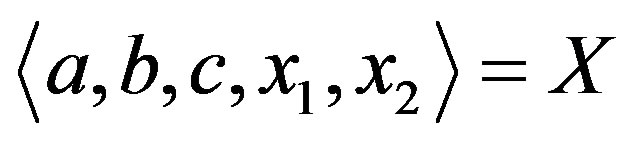 .
.
Let . Clearly
. Clearly 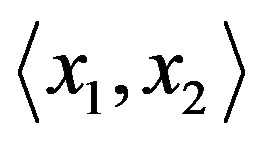 acts transitively on
acts transitively on , which follows X acts 2-transitively on
, which follows X acts 2-transitively on and hence primitively, on
and hence primitively, on . Let
. Let . Then
. Then
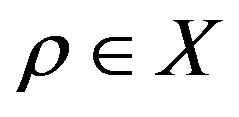 and X contains a 5-cycle
and X contains a 5-cycle
 . Noting that every generator of X is even permutation,
. Noting that every generator of X is even permutation, 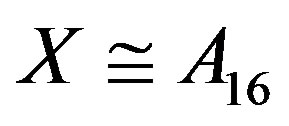 by [16, Theorem 3.3E]. Then the stabilizer
by [16, Theorem 3.3E]. Then the stabilizer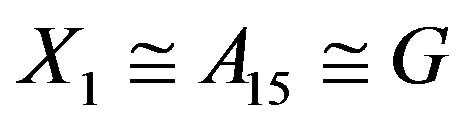 . On the other hand H acts regularly on
. On the other hand H acts regularly on  leads to that
leads to that 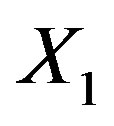 acts regularly on
acts regularly on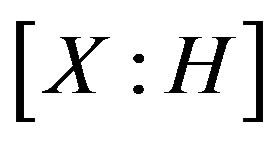 . Simple computation shows
. Simple computation shows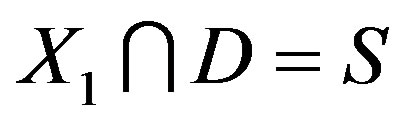 . Hence
. Hence 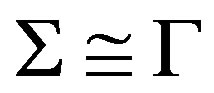 by Proposition 1.1, and furthermore
by Proposition 1.1, and furthermore 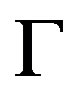 is connected by the connectivity of
is connected by the connectivity of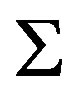 . Namely
. Namely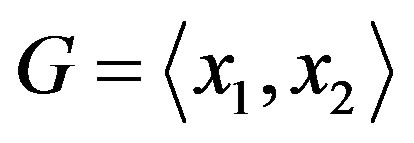 , which leads to
, which leads to . However
. However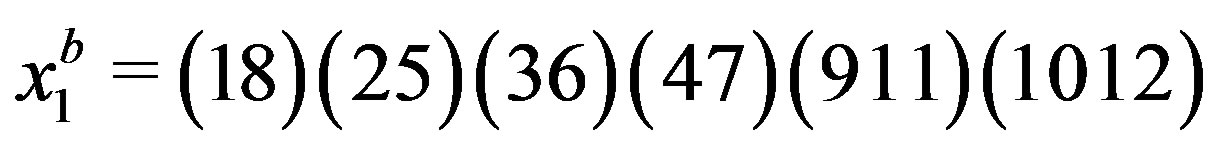 , which changes 1. Thus
, which changes 1. Thus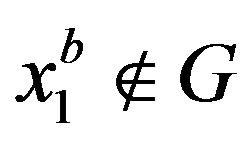 , i.e., G is not normal in X.
, i.e., G is not normal in X.
Example 2.2 Let G be the alternating group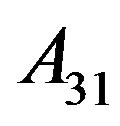 .
.
Set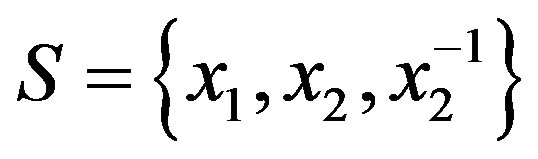 , where
, where

Let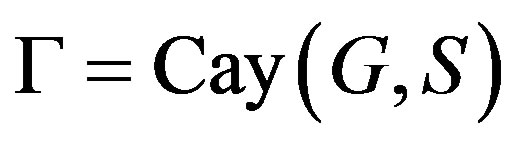 , then
, then 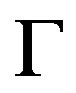 is cubic nonsymmetric connected Cayley graph, which is not normal.
is cubic nonsymmetric connected Cayley graph, which is not normal.
Let 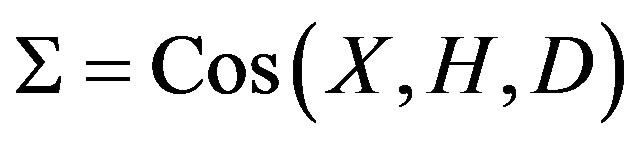 be a connect vertex-transitive graph, where
be a connect vertex-transitive graph, where 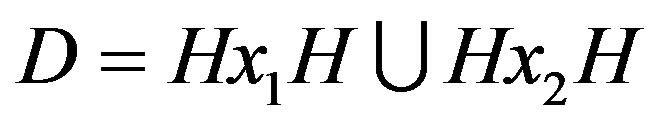 and
and 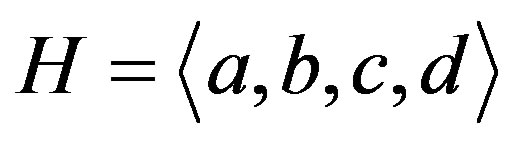 with
with

It is trivial for us to get  with 1, 5 and 9 being in different orbits, then
with 1, 5 and 9 being in different orbits, then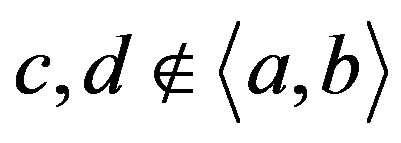 . By simple checking, we find
. By simple checking, we find  and
and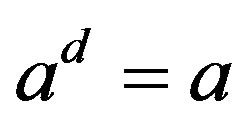 . It follows
. It follows
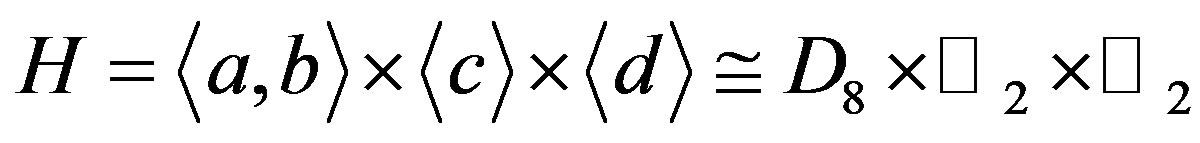 .
.
Note that 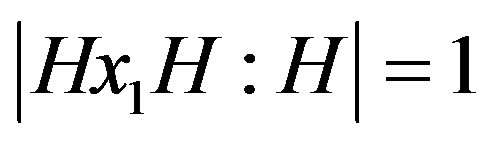 and
and , then
, then
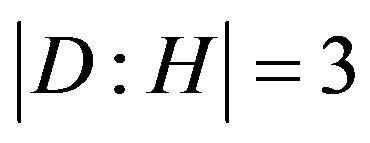 . Namely the valency of
. Namely the valency of  is
is . However
. However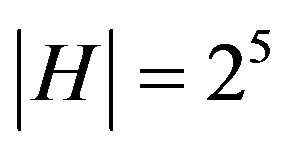 , thus
, thus  is nonsymmetric. Notice that
is nonsymmetric. Notice that  is connected, i.e.,
is connected, i.e.,
 .
.
Set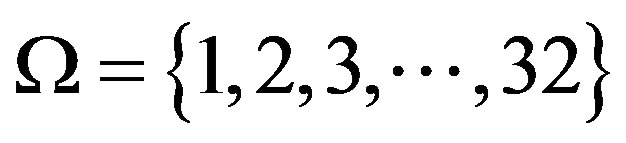 . Clearly
. Clearly 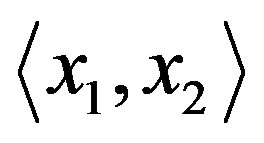 acts transitively on
acts transitively on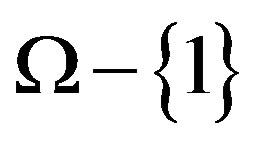 , and then X acts 2-transitively on
, and then X acts 2-transitively on
 , and hence primitively, on
, and hence primitively, on . Let
. Let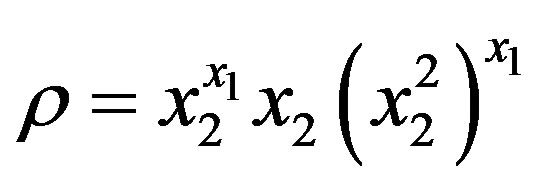 .
.
Then 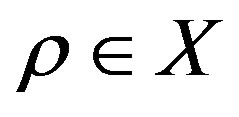 and X contains a 17-cycle
and X contains a 17-cycle
 .
.
Note that all generators of X are even permutations, then 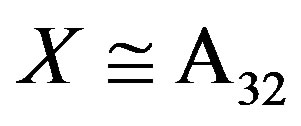 by [16, Theorem 3.3E]. Then the stabilizer
by [16, Theorem 3.3E]. Then the stabilizer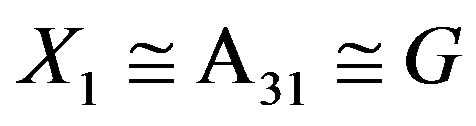 . Noting H acts regularly on
. Noting H acts regularly on ,
,
 acts regularly on
acts regularly on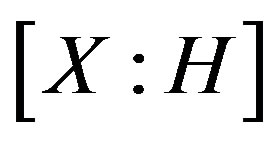 . It is shown, by computing, that
. It is shown, by computing, that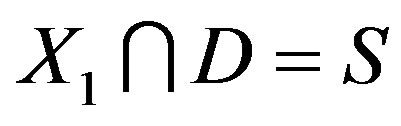 . That is
. That is 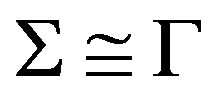 by Proposition 1.1. And moreover the connectivity of
by Proposition 1.1. And moreover the connectivity of 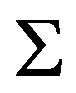 leads to
leads to  is also connected. Hence
is also connected. Hence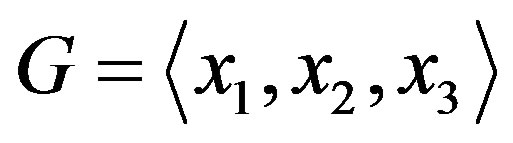 , i.e.,
, i.e.,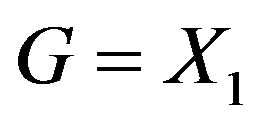 . However
. However
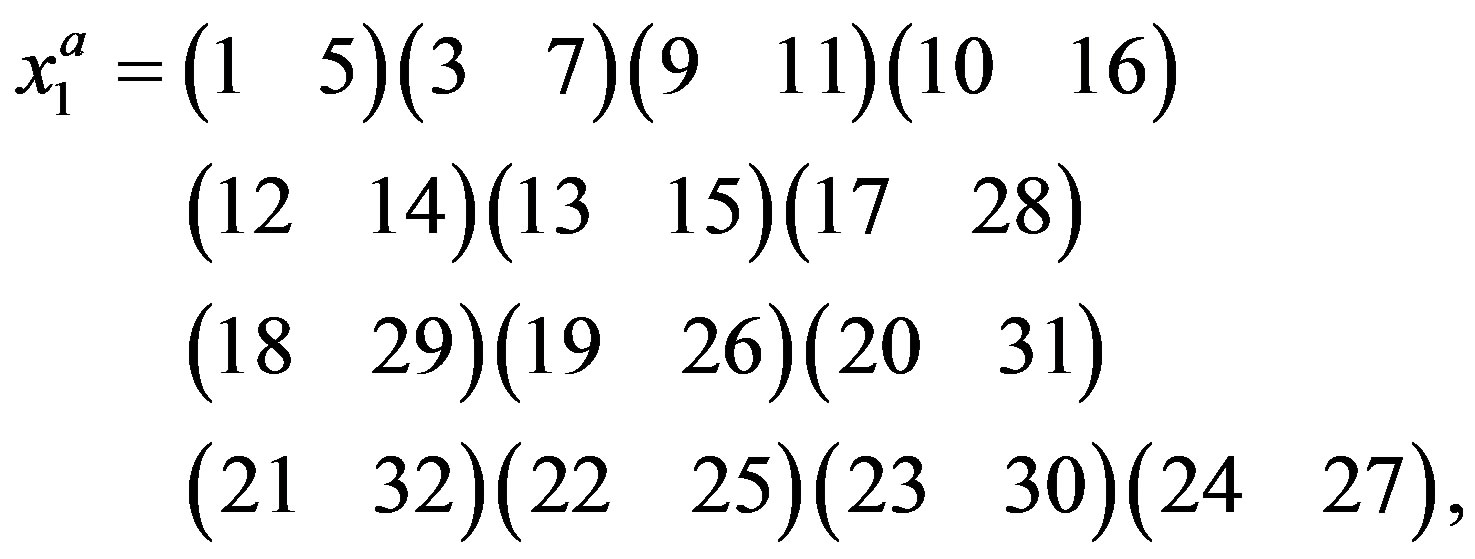
which changes 1. Thus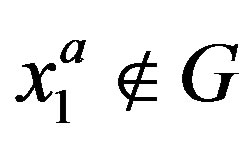 , i.e.,
, i.e., 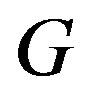 is not normal in X.
is not normal in X.
REFERENCES
- N. Biggs, “Algebraic Graph Theory,” 2nd Edition, Cambridge University Press, New York, 1992.
- J. J. Li and Z. P. Lu, “Cubic s-Transitive Cayley Graphs,” Discrete Mathematics, Vol. 309, No. 28, 2009, pp. 6014-6025. doi:10.1016/j.disc.2009.05.002
- P. Lorimer, “Vertex-Transitive Graphs: Symmetric Graphs of Prime Valency,” Journal of Graph Theory, Vol. 8, No. 1, 1984, pp. 55-68. doi:10.1002/jgt.3190080107
- G. O. Sabidussi, “Vertex-Transitive Graphs,” Monatshefte für Mathematik, Vol. 68, No. 5, 1964, pp. 426-438. doi:10.1007/BF01304186
- W. T. Tutte, “A Family of Cubical Graphs,” Proceedings of the Cambridge Philosophical Society, Vol. 43, No. 4, 1947, pp. 459-474. doi:10.1017/S0305004100023720
- W. T. Tutte, “On the Symmetry of Cubic Graphs,” Canadian Journal of Mathematics, Vol. 11, No. 3, 1959, pp. 621-624. doi:10.4153/CJM-1959-057-2
- D. Ž. Djokovic, “On Regular Graphs, II,” Journal of Combinatorial Theory, Series B, Vol. 12, No. 3, 1972, pp. 252-259. doi:10.1016/0095-8956(72)90039-1
- A. Gardiner, “Doubly-Primitive Vertex Stabilisers in Graphs,” Mathematische Zeitschrift, Vol. 135, No. 3, 1974, pp. 257-266. doi:10.1007/BF01215029
- A. Gardiner, “Arc-Transitivity in Graphs. II,” Quarterly Journal of Mathematics Oxford Series, Vol. 25, No. 2, 1974, pp. 163-167. doi:10.1093/qmath/25.1.163
- A. Gardiner, “Arc-Transitivity in Graphs. III,” Quarterly Journal of Mathematics Oxford Series, Vol. 27, No. 1, 1976, pp. 313-323. doi:10.1093/qmath/27.3.313
- D. Ž. Djokovic and G. L. Miller, “Regular Graphs of Automorphisms of Cubic Graphs,” Journal of Combinatorial Theory, Series B, Vol. 29, No. 1, 1980, pp. 195-230. doi:10.1016/0095-8956(80)90081-7
- R. Weiss, “S-Transitive Graphs,” Algebraic Methods in Graph Theory, Vol. 25, No. 1, 1981, pp. 827-847.
- X. G. Fang, C. H. Li, J. Wang and M. Y. Xu, “On Cubic Normal Cayley Graphs of Finite Simple Groups,” Discrete Mathematics, Vol. 244, No. 1, 2002, pp. 67-75. doi:10.1016/S0012-365X(01)00075-9
- C. H. Li, “Isomorphisms of Finite Cayley Graphs,” Ph.D. Dissertation, Department of Mathematics of University of Western Australia, 1996.
- S. J. Xu, X. G. Fang, J. Wang and M. Y. Xu, “5-Arc Transitive Cubic Cayley Graphs on Finite Simple Groups,” European Journal of Combinatorics, Vol. 28, No. 3, 2007, pp. 1023-1036. doi:10.1016/j.ejc.2005.07.020
- J. D. Dixon and B. Mortimer, “Permutation Groups,” Springer-Verlag Press, New York, 1996.
NOTES
*The project sponsored by the scientific research foundation of Guangxi University (Grant No. XBZ110328), the fund of Yunnan University (No. 2012CG015), the National Natural Science Foundation of China (No. 11126343) and (No. 11171292), and NSF of Guangxi (No. 2012- GXNSFBA053010).
#Corresponding author.

