Optics and Photonics Journal
Vol.2 No.3(2012), Article ID:22489,4 pages DOI:10.4236/opj.2012.23026
Schrödinger Equation with a Cubic Nonlinearity Sech-Shaped Soliton Solutions
Institut Henri Poincaré, Le Vésinet, France
Email: pierre.hillion@wanadoo.fr
Received June 3, 2012; revised July 1, 2012; accepted July 12, 2012
Keywords: Soliton; Schrödinger Equation; Cubic Nonlinearity
ABSTRACT
We first analyze the sech-shaped soliton solutions, either spatial or temporal of the 1D-Schrödinger equation with a cubic nonlinearity. Afterwards, these solutions are generalized to the 2D-Schrödinger equation in the same configuration and new soliton solutions are obtained. It is shown that working with dimensionless equations makes easy this generalization. The impact of solitons on modern technology is then stressed.
1. Introduction
The one dimensional Schrödinger equation with a cubic nonlinearity has been known for a long time as well as its analytical solutions in terms of sech-shaped functions.Till recently, the situation was different for the two dimensional Schrödinger equation that we shall discuss here.
Using general equations, we start with the spatial and temporal sech-shaped soliton solutions of the 1DSchrödinger equation with a cubic nonlinearity and it is shown that working with dimensionless equations leads to further types of solitons. Then, the same process with gene-ral and dimensionless equations is applied to the 2D-nonlinear Schrödinger equation which has sech-shaped soliton solutions generalizing 1D-solitons. Finally, because the nonlinear Schrödinger equation is a universal model that describes many physical non linear systems, the importance of solitons in modern technology is stressed. Nonlinear Schrödinger equations in (3D) and in cylindrical coordinates are succinctly discussed in Section 4.
2. One Dimensional Sech-Shaped Solitons
2.1. General Equations
The one-dimensional, cubic, nonlinear Schrödinger Equation [1] intervenes in different physical settings to describe wave propagation in fluids, plasmas… nonlinear optics [2-6] in one of the three forms (c is the light velocity, k the wave number of propagating waves, c is a positive dimensionless parameter characterizing the medium in which this propagation takes place).
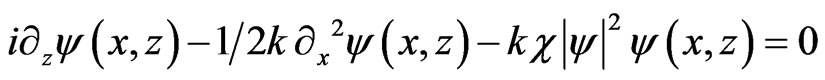 (1a)
(1a)
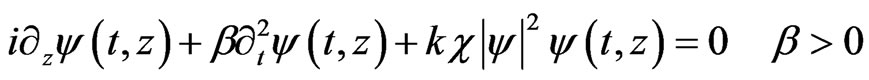 (1b)
(1b)
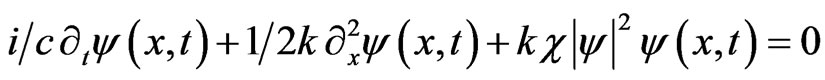 (1c)
(1c)
It is known to be one of the simplest partial differential equations with complete integrability, admetting in particular Nth order solitons as solutions and called spatial and temporal when they are solutions of (1a) or (1b). Changing the sign of the last term on the left hand side of Equations (1a)-(1c) gives a second set of cubic nonlinear Schrödinger equations with quasi periodic but no soliton sech-shaped solutions.
It is easy to prove that the first order soliton solution of Equation (1a) with amplitude A is [6]
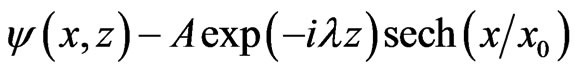 (2)
(2)
with
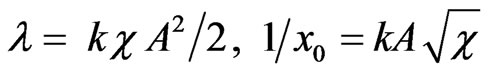 (2a)
(2a)
Indeed:
 (3a)
(3a)
while
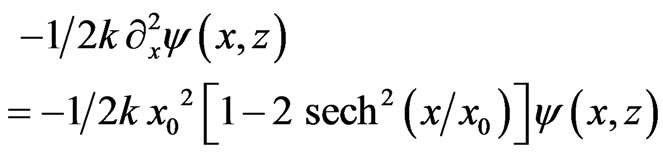 (3b)
(3b)
 (3c)
(3c)
Substituting (3a) and (3c) into (1a) proves the result and, changing z, k into ct, -k in (2) gives the first order soliton solution of Equation (1c) while the solution of (1b) is [6] easy to check
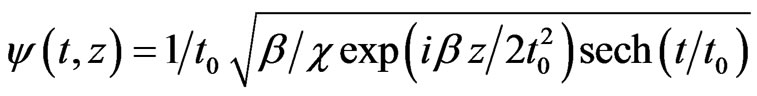 (4)
(4)
These solutions have the remarkable feature that their profile does not evolve during propagation.
2.2. Dimensionless Equations
Using the dimensionless coordinates z = kz, 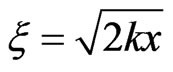 , t = kct the Equations (1a) and (1c) take the simple form (5a) and (5c)
, t = kct the Equations (1a) and (1c) take the simple form (5a) and (5c)
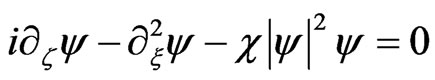 (5a)
(5a)
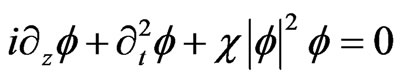 (5b)
(5b)
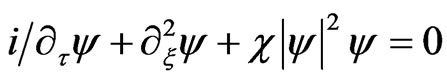 (5c)
(5c)
while the Equation (5b) is obtained with [7]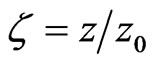 ,
, 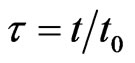 ,
, 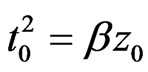 ,
,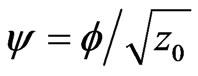 .
.
But, there exist more general expressions of the first order solitons for instance, for the Equation (5c) rewritten with the coordinates x, z, t, we have
 (6)
(6)
in which A, B, C1, C2 are arbitrary real constant with in particular [7]
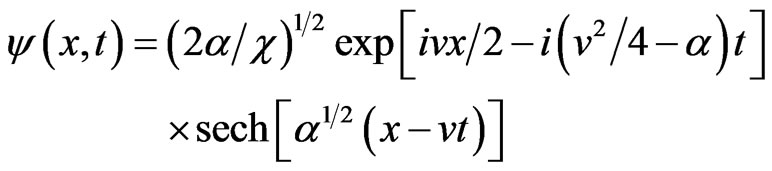 (6a)
(6a)
Similarly, with Equation (5a) also rewritten with x, z, we get as solution in which β is a dimension-less parameter
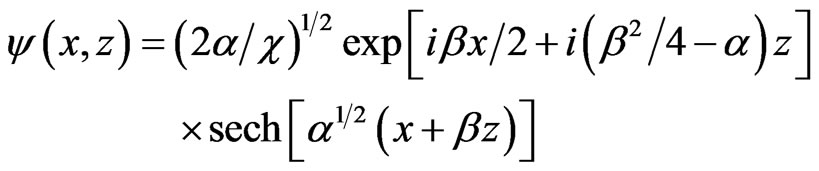 (7)
(7)
The higher order soliton solutions have more intricate expressions [8] and their profile is no more constant, the solutions being rather periodic than stationary. The profile of a N = 2 soliton is pictured in [3].
The Equation (5b) has the simple solution [6]
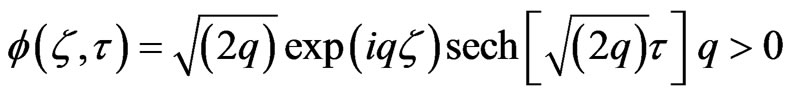 but, the comparison of (5b) and (5c) shows that changing x, t, y into t, z, f in (6a) gives another solution of (5b)
but, the comparison of (5b) and (5c) shows that changing x, t, y into t, z, f in (6a) gives another solution of (5b)
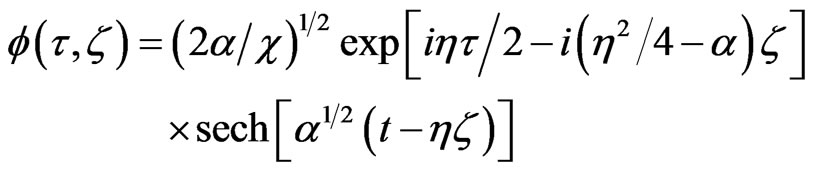 (8)
(8)
where to avoid confusion h has ben used instead of v.
3. Two Dimensional Sech-Shaped Solitons
3.1. General Equations
The situation is somewhat different for the two dimensional cubic nonlinear Schrödinger equations (cylindrical coordinates are used in (9b))
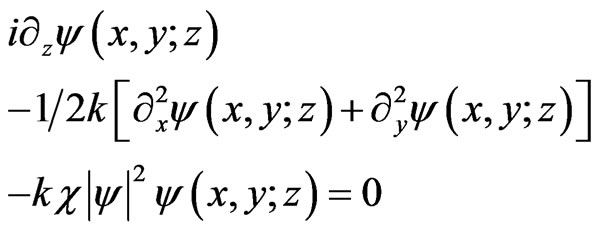 (9a)
(9a)
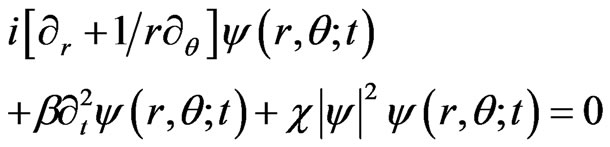 (9b)
(9b)
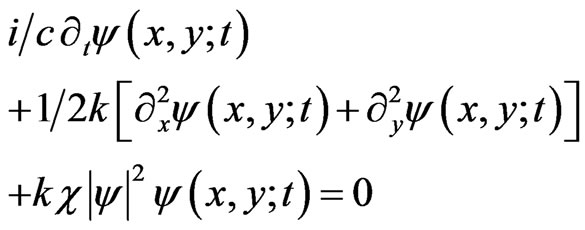 (9c)
(9c)
They where devoted to some domains, mainly hydrodynamics and mechanics [9-11] till that recently nonlinearities became an important topic, specially in optics and photonics, with as consequence to boost works on the analysis of Equations (9).
We prove here that Equation (9a) have soliton-shaped solutions generalizing (2)
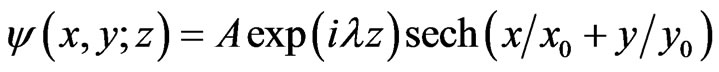 (10)
(10)
with
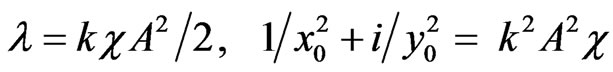 (10a)
(10a)
We first have
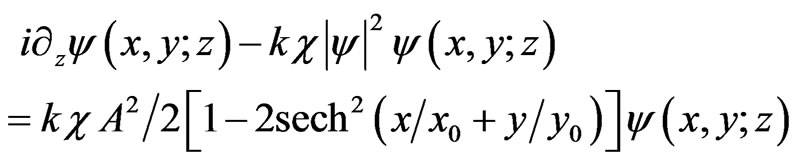 (11a)
(11a)
and according to (3b) together with the second relation (10a)
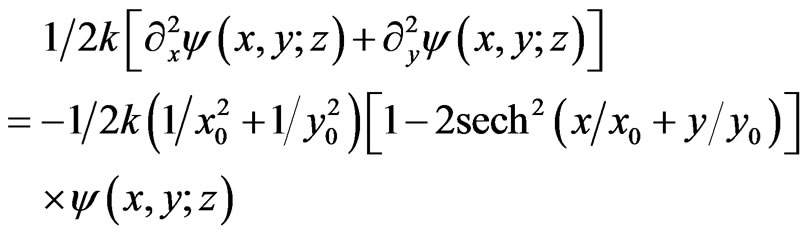 (11b)
(11b)
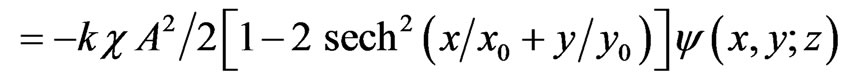 (11c)
(11c)
Substituting (11a) and (11c) into (9a) achieves the proof. Changing z, k into ct, −k in (10) gives the soliton-shaped solution  of Equation (9c).
of Equation (9c).
3.2. Dimensionless Equations
The two dimensional generalization of Equation (5c), that is (9c) with dimensionless coordinates, is
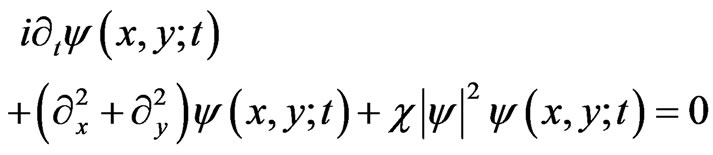 (12)
(12)
We look for the solutions of this equation in the form
 (13)
(13)
in which  while a, r, s are real parameters and, to symplify we write exp(.) the exponential factor. Then, a simple calculation gives
while a, r, s are real parameters and, to symplify we write exp(.) the exponential factor. Then, a simple calculation gives
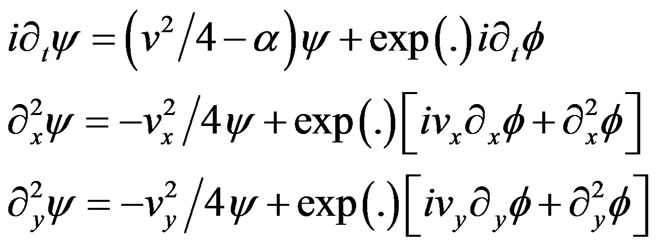 (14)
(14)
Substituting (13) into (12) gives the equation satisfied by f with 
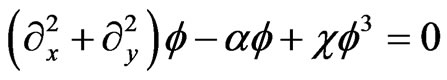 (15)
(15)
and we look for the solutions of (15) in the form
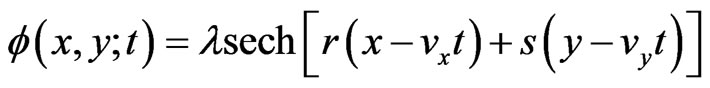 (16)
(16)
in which l, r, s are real parameters to be determined. Writing to simplify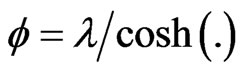 , we get
, we get
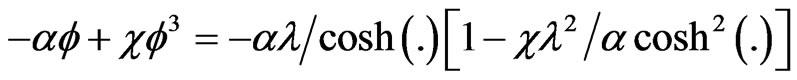 (17)
(17)
and
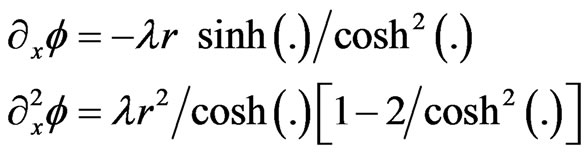 (18a)
(18a)
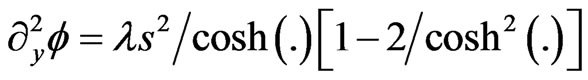 (18b)
(18b)
substituting (17) and (18a,b) into (15) gives
 (19)
(19)
implying
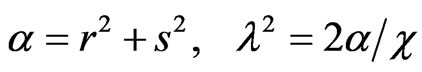 (19a)
(19a)
so that the solution (16) becomes with 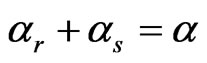
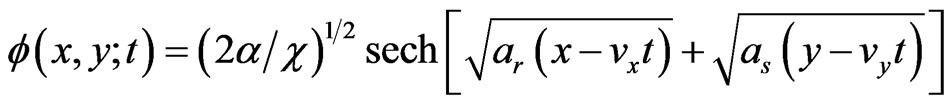 (20)
(20)
to be compared with (6a).
Similarly the two dimensional generalization of (5a), that is (9a) with dimensionless coordinates, is
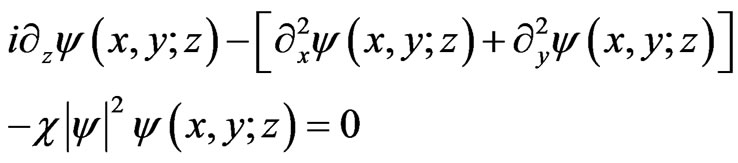 (21)
(21)
with the solutions in which  and
and 
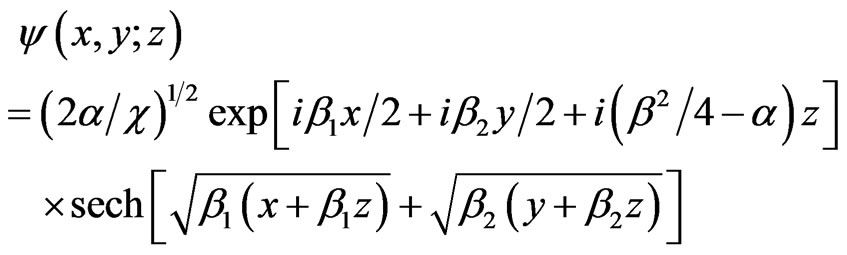 (22)
(22)
We are left with Equation (9b). Then, using the dimensionless coordinates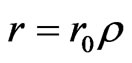 ,
, 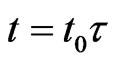 ,
, 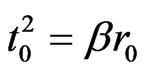 ,
, 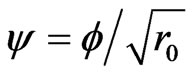 in which r and r0 positive. we get
in which r and r0 positive. we get
 (23)
(23)
We look for the solution of this equation in the form
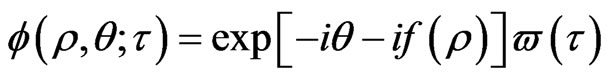 (24)
(24)
with 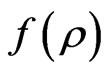 satisfying the equation
satisfying the equation
 (24a)
(24a)
Substituting (24) into (23) and taking into account (24a) give
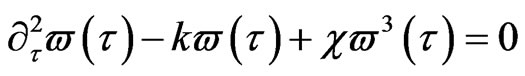 (25)
(25)
with the solution [7]
 (25a)
(25a)
while the solution of (24a) is
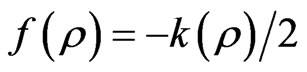 (26)
(26)
substituting (25a) and (26) into (24) we get finally
 (27)
(27)
in which v is an arbitrary real parameter. It does not seem that the sech-shaped soliton (27) is known. But, substituting the dimensionless coordinate  to
to 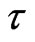 into (27) gives the sech-shaped pulse
into (27) gives the sech-shaped pulse
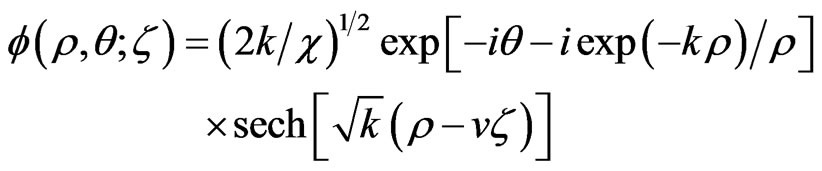 (28)
(28)
4. Two Generalizations
4.1. 3D-Schrödinger Equation
Using the index 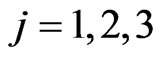 for the dimensionless coordinates x,y,z together with the sum-mation convention on the repeated indices and
for the dimensionless coordinates x,y,z together with the sum-mation convention on the repeated indices and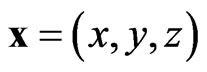 , the tridimensional cubic nonlinear Schrödinger equation is
, the tridimensional cubic nonlinear Schrödinger equation is
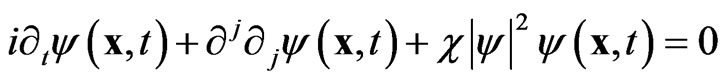 (29)
(29)
We look for the solution of this equation in the form 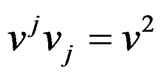
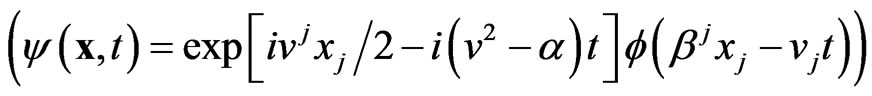 (30)
(30)
the exponential term is written exp(.) to simplify and a simple calculation gives
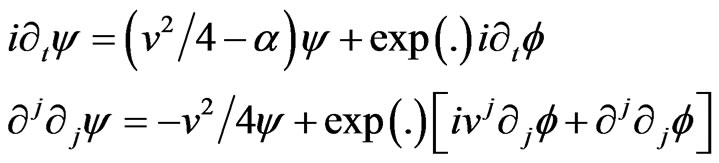 (31)
(31)
Since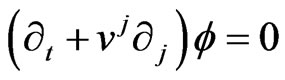 , substituting (31) into (30) gives the equation satisfied by f
, substituting (31) into (30) gives the equation satisfied by f
 (32)
(32)
We look for its solutions in the form with the real parameters l, 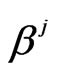 to be determined
to be determined
 (33)
(33)
and writing 1/cosh(.) for , we get
, we get
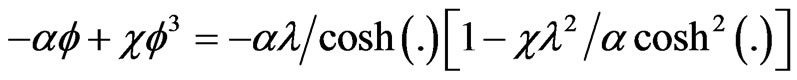 (34a)
(34a)
and 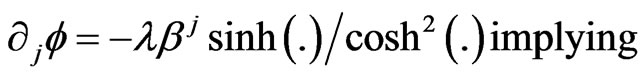
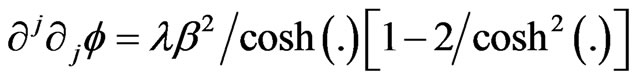 (34b)
(34b)
Substituting (34) into (32) gives
 (35)
(35)
implying
 (36)
(36)
which achieves to determine (33) and consequently the solution (30) of the three dimensional cubic nonlinear Schrödinger equation
4.2. Schrödinger Equation in Cylindrical Coordinates
Using the dimensionless coordinates r, θ, f, the Schrödinger equation with a cubic non linelarity is
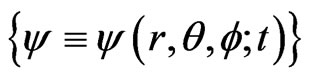
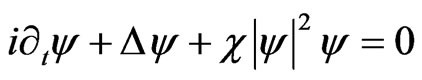 (37)
(37)
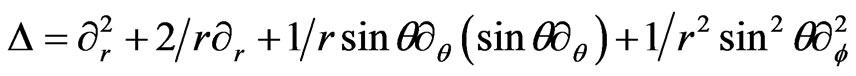 (37a)
(37a)
For fields that do not depend on q, f, this equation reduces to
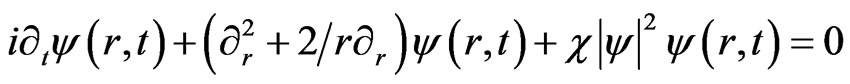 (38)
(38)
and assuming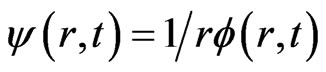 , we get
, we get
 (39)
(39)
so that
 (40)
(40)
and Equation (38) becomes
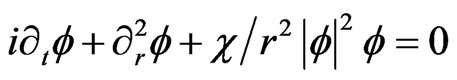 (41)
(41)
We look for the solutions of this equation in the form
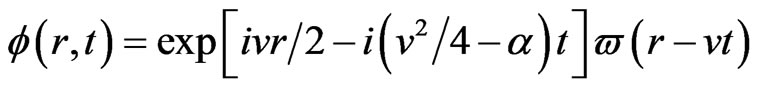 (42)
(42)
and a simple calculation gives, exp(.) representing the exponential term.
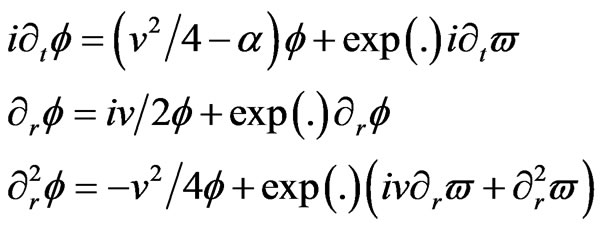 (43)
(43)
Substituting (42) into (41) and taking into account (43), we get since 
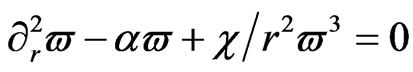 (44)
(44)
We look for the solutions of this equation in the form with the real parameters β, l to be de-termined
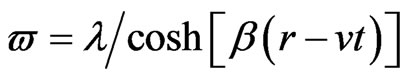 (45)
(45)
Writing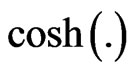 ,
, 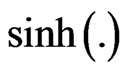 for hyperbolic functions, a simple calculation gives
for hyperbolic functions, a simple calculation gives
 (46)
(46)
Substituting (45) and (46) into (44) gives
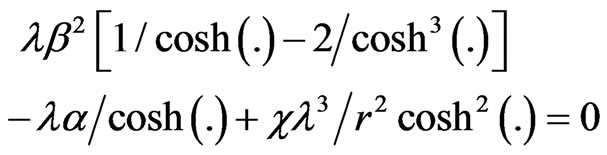 (47)
(47)
that is
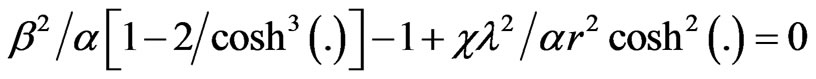 (48)
(48)
We consider an asymptotic approximation of this equation for 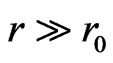 with
with 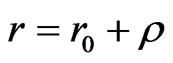 so that to the order
so that to the order 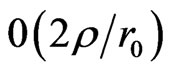 Equation (48) becomes
Equation (48) becomes
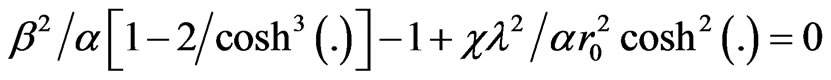 (48a)
(48a)
with the solution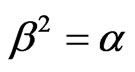 ,
,  which achieves to determine the spherical solution of the cubic nonlinear Schrödinger equation.
which achieves to determine the spherical solution of the cubic nonlinear Schrödinger equation.
5. Conclusions
The nonlinear Schrödinger equation describes physical processes in which nonlinearity and dispersion cancel giving birth to solitons. This equation [9-11] can be applied to hydrodynamics (rogue waves), nonlinear optics (optical solitons in Kerr media), nonlinear aoustics (blood circulation), quantum condensates (Bose-Einstein), heath waves… All these processes lead to the generation of solitons along pulse propagation: An example is supplied by the optical solitons that travel without distortion justifying their importance [12-15] for laser pulse propagation in optical fibers.
Two dimensional solitons present a great interest since they propagate in lattices [16,17] as well as surface waves [18-21]. Some works were recently devoted to the 2Doptical solitons [22,23] and the sech-shaped solutions (20), (21) of Equations (9a) and (9c) are a particular case of the spatial temporal solutions discussed in [23].
No doubt that some of the 2D sech-shaped solitons discussed here will find practical applications in a near future.
REFERENCES
- T. Oh and C. Sulem, “On One Dimensional Cubic Nonlinear Schrödinger Equation,” arXiv: 10072018, 2010.
- N. N. Akhmediev, “Spatial Solitons in Kerr and KerrLike Media,” Optical and Quantum Electronics, Vol. 30, No. 7-10, 1998, pp. 535-569. doi:10.1023/A:1006902715737
- J. G. New, “Introduction to Nonlinear Optics,” Cambridge University Press, Cambridge, 2011. doi:10.1017/CBO9780511975851
- G. Gryndberg, A. Aspect and Cl. Fabre, “Introduction to Quantum Optics,” Cambridge University Press, Cambridge, 2010.
- C. Q. Dai, Z. Q. Qin and C. L. Zheng, “Multisoliton Solutions of the Modified Nonlinear Schrö-Dinger Equation,” Physica Scripta, Vol. 85, No. 4, 2012, Article ID: 045007. doi:10.1088/0031-8949/85/04/045007
- C. J. Brenton, “Solitons and Nonlinear Optics in SiliconOn Insulator Photonics Wires,” Thesis, 2009.
- G. B. Whitham, “Linear and Nonlinear Wave Equations,” Wiley, New York, 1974.
- Eq. World (Google), “Shrödinger Equation with a Cubic Nonlinearity,”
- J. Bourgain, “Nonlinear Schrödinger Equation,” Parc City Lectures, 1995.
- R. Killip, T. Tao and M. Visam, “The Cubic Nonlinear Schrödinger Equation in Two Dimen-Sions with Radial Data,” Journal of the European Mathematical Society, Vol. 11, No. 6, 2009, pp. 1203-1258. doi:10.4171/JEMS/180
- A. R. Seadway, “Exact Solutions of a Two Dimensional Nonlinear Schrödinger Equation,” Applied Mathematics Letters, Vol. 25, 2012, pp. 687-691.
- J. C. Bronski, M. Segev and M. Weinstein, “Mathematical Frontiers in Optical Solitons,” Proceedings of the National Academy of Sciences, Vol. 98, No. 23, 2001, pp. 12872-12873.
- Z. H. Muslinami, K. G. Makris, R. EL-Ganaini and D. N. Christodoulides, “Optical Solitons in PT Periodic Potentials,” Physical Review Letters, Vol. 100, 2006, Article ID: 030402.
- Y. V. Kartshov, “Optical Lattice Solitons: Guiding and Routing Light at Will,” OSA Optics and Photonics Focus, 2009.
- F. I. Khatri, “Optical Soliton Propagation and Control,” MIT Thesis, Massachusetts Institute of Technology, Cambridge, 1996.
- Y. V. Kartshov, J. A. Malomed, V. A. Vysloukh and L. Torner, “Two Dimensional Solitons in Nonlinear Lattices,” Optics Letters, Vol. 34, No. 6, 2009, pp. 770-777. doi:10.1364/OL.34.000770
- M. J. Ablowitz, B. Ilan, E. Schonbrun and R. Piestun, “Two Dimensional Solitons in Irregular Lattices,” Theoretical and Mathematical Physics, Vol. 151, No. 3, 2007, pp. 723-734. doi:10.1007/s11232-007-0058-4
- G. Maugin, “Nonlinear Surface Wave and Solitons,” The European Physical Journal, Vol. 147, No. 1, 2007, pp. 209-230.
- X. Wang, A. Bezryadina, Z. ChenK, G. Magris, D. N. Christodoulides and G. I. Stegman, “Observation of a Two Dimensional Surface Soliton,” Physical Review, Vol. 98, 2007, Article ID: 123903.
- Y. Kominis, A. Papadopoulos and K. Hizanidis, “Surface Solitons in Wave Guide Arrays; Analytical Solutions,” Optics Express, Vol. 15, No. 16, 2007, pp. 10041-10051. doi:10.1364/OE.15.010041
- Y. V. Kartshov, V. A. Vysloukh and L. Torner, “Generation of Surface Soliton Arrays,” Optics Letters, Vol. 31, No. 15, 2006, pp. 2329-2331. doi:10.1364/OL.31.002329
- N. K. Efremides, J. Hudlock, D. N. Christodoulides, J. W. Fleischer, D. Cohen and M. Segev, “Two Dimensional Optical Lattice Solitons,” Physical Review Letters, Vol. 91, No. 21, 2003, pp. 1-4.
- B. A. Malomed, D. Mialache, F. Wise and L. Torner, “Spatial Temporel Solitons,” Journal of Optics B: Quantum and Semiclassical Optics, Vol. 7, No. 5, 2005, pp. R53-R72. doi:10.1088/1464-4266/7/5/R02

