American Journal of Computational Mathematics
Vol.05 No.02(2015), Article ID:57024,7 pages
10.4236/ajcm.2015.52011
First Integral Method: A General Formula for Nonlinear Fractional Klein-Gordon Equation Using Advanced Computing Language
Mohamed A. Abdoon
Mathematics Department, Sudan University of Science and Technology, Khartoum, Sudan
Email: moh.abdoon@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 March 2015; accepted 5 June 2015; published 10 June 2015
ABSTRACT
In this article, a general formula of the first integral method has been extended to celebrate the exact solution of nonlinear time-space differential equations of fractional orders. The proposed method is easy, direct and concise as compared with other existent methods.
Keywords:
First Integral Method, Exact Solution, Fractional Klein-Gordon Equation

1. Introduction
Partial differential equations arise frequently in the formulation of fundamental laws of nature and in the mathematical analysis of a wide variety of problems in applied mathematics, mathematical physics, and engineering science. This subject plays a central role in modern mathematical sciences. In recent years, it has turned out that many phenomena in fluid mechanics, viscoelasticity, biology, physics, engineering and other areas of science can be successfully modeled by the use of fractional derivatives and integrals [1] [2] . In this article, we study fractional differential equations associated with derivatives. Such a kind of equation appears in many problems. In particular, we have found fractional differential equations related to the classical Klein-Gordon equation [3] .
2. Preliminaries and Basic Definitions and First Integral Method
The Jumarie’s modified Riemann-Lionvile derivative, of order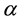 , can be defined by the following expression
, can be defined by the following expression
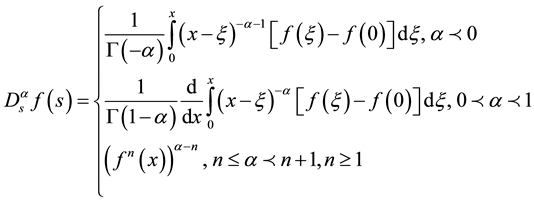 (1)
(1)
Moreover, some properties for the modified Riemann-Liouville derivative can be given as follows:
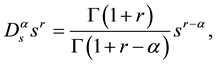 (2)
(2)
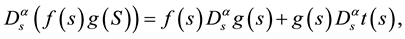 (3)
(3)
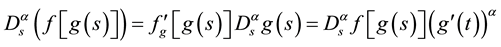 (4)
(4)
Consider the time fractional differential equation with independent variables 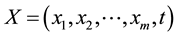 and a dependent variable
and a dependent variable ,
,
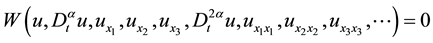 (5)
(5)
Using the variable transformation
 (6)
(6)
where 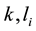 and
and  are constants to be determined later. The fractional differential Equation (5) is reduced to a nonlinear ordinary differential equation
are constants to be determined later. The fractional differential Equation (5) is reduced to a nonlinear ordinary differential equation
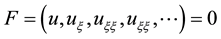 (7)
(7)
We assume that Equation (7) has a solution in the form
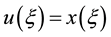 (8)
(8)
and introduce a new independent variable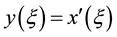 ,which leads to a new system of ordinary differential equations
,which leads to a new system of ordinary differential equations
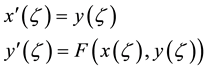 (9)
(9)
By using the division theorem for two variables in complex domain  which is based on the Hilbert- Nullstellensatz theorem [4] , we can obtain a first integral to Equation (9) which can applied to Equation (7) to obtain a first-order ordinary differential equation. An exact solution to Equation (5) is then obtained by solving the equations that are obtained from applying Equation (9) into Equation (7). Now, we wish to quickly recall the division theory.
which is based on the Hilbert- Nullstellensatz theorem [4] , we can obtain a first integral to Equation (9) which can applied to Equation (7) to obtain a first-order ordinary differential equation. An exact solution to Equation (5) is then obtained by solving the equations that are obtained from applying Equation (9) into Equation (7). Now, we wish to quickly recall the division theory.
Theorem 2.1 [The Division Theorem]
Suppose that 











3. The First Integral Method: A General Formula
We discuss the problem by using the first integral method and consider the general formula [5] :

where 
Substituting Equation (7) in Equation (6), we get the system

Now, we apply the division theorem. Suppose that 


which is an irreducible Polynomial in the complex domain






which can be written as

by comparing the coefficients of 




from (12a), we deduce that 




Case (1)
When



Since 

For simplicity, we take


Suppose that


where 


Substituting Equation (16) in Equation (10), we obtain

By combining Equation (20) with Equation (11), we find the exact solution of Equation (11).
Case (2)
When M = 2, in Equation (15), then the Equation (16) became




Since 

For simplicity, we take



Suppose that


where 
By substituting 

Using Equation (23) in Equation (12), we obtain two equal roots for Y.
Note that

Combining Equation (24) with Equation (11), we find the exact solution of Equation (11).
Case 3
When M = 3, in Equation (15), then the Equation (16) become





Since 

For simplicity, we take


Suppose that




where 
Substituting 

Substituting Equation (23) in Equation (12), we obtain three equal roots for Y
Note that

then
Combining Equation (24) with Equation (11), we find the exact solution of Equation (11).
By the integrating Equations (20), (25) and (30), we can find different solutions of Equation (10), and the exact solution of the general formula in Equation (10) are given by combining Equations (20), (24), (30), with (11) and integrating respect with respect to
We can apply Theorem 3.1 to studying some time fractional differential equations.
4. Applications
The Space-Time Fractional Klein-Gordon Equation [6] :
Consider the nonlinear fractional Klein-Gordon equation,

For our purpose, we introduce the following transformations

where 
Substituting Equation (33) in Equation (32)

which is the same as in the form of Equation (10) where



Integrating with respect to 




where
where 
Consider the initial condition (32), we can see that the generalized the nonlinear fractional Klein-Gordon Equation (32) have the exact solution
Comparing our results with that of resalts [6] , shows the novelty of our solution. See Appendix A Figure 1.
5. Conclusion
A general formula of the first integral method is used successfully to solve systems of nonlinear fractional differential equations. The performance of this method is reliable, effective and gives more solutions. We have extended the general formula to solve other fractional differential equations.
References
- Feng, Z. (2004) Exact Solutions for the Lienard Equation and Its Applications. Chaos, Soliton & Fractals, 21, 343-348. http://dx.doi.org/10.1016/j.chaos.2003.10.025
- Golmankhaneh, A.K. and Baleanu, D. (2011) On Wave Nonlinear Fractional Klein-Gordon Equation. Signal Process- ing, 91, 446-451. http://dx.doi.org/10.1016/j.sigpro.2010.04.016
- Feng, Z.S. (2002) The First Integer Method to Study the Burgers-Korteweg-de Vries Equation. Journal of Physics A, 35, 343. http://dx.doi.org/10.1088/0305-4470/35/2/312
- Zhou, Y.B., Wang M.L. and Wang, Y.M. (2003) Periodic Wave Solution to a Coupled Kdv Equation with Variable Coefficients. Physics Letters A, 308, 31-36.
- Abdoon, M. (2015) Programming First Integral Method General Formula for the Solving Linear and Nonlinear Equations. Applied Mathematics, 6, 568-575. http://dx.doi.org/10.4236/am.2015.63051
- Ahmed Ali, A. H. and Raslan, K. (2007) New Solutions for Some Important Partial Differential Equations. International Journal of Nonlinear Science, 4, 109-117.
Appendix A Figure1
Figure 1. Graph of the solution u (x, t) corresponding to the values of α, λ, L and b as shown in the caption.












