American Journal of Computational Mathematics
Vol.04 No.04(2014), Article ID:50195,8 pages
10.4236/ajcm.2014.44030
Effect of Variable Viscosity, Dufour, Soret and Thermal Conductivity on Free Convective Heat and Mass Transfer of Non-Darcian Flow past Porous Flat Surface
Isaac L. Animasaun1, Anselm O. Oyem2
1Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria
2Department of Mathematics, Federal University Lokoja, Lokoja, Nigeria
Email: Onyekachukwu.oyem@fulokoja.edu.ng, reallityo@yahoo.co.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 August 2014; revised 2 September 2014; accepted 10 September 2014
ABSTRACT
The motion of incompressible fluid of a variable fluid viscosity and variable thermal conductivity with thermal radiation, Dufour, Soret with heat and mass transfer over a linearly moving porous vertical semi-infinite plate with suction is investigated. The governing equations are transformed into a system of coupled nonlinear ordinary differential equations using similarity transformations with dimensionless variables and solved numerically using shooting method with Runge- Kutta fourth-order method and Newton-Raphson’s interpolation scheme implemented in MATLAB. The result showed that with increase in Dufour and Soret parameter, fluid velocity increases and temperature increases with increase in variation of Dufour while, temperature decreases with increase in Soret. The effects of variable fluid viscosity, variable thermal conductivity, thermal radiation, Soret, Dufour, Prandtl and Schmidt parameters on the dimensionless velocity, temperature and concentration profiles are shown graphically.
Keywords:
Variable Viscosity, Variable Thermal Conductivity, Non-Darcian Flow, Free Convection, Dufour, Soret, Porous Flat Surface

1. Introduction
Fluid flow problems of free convective, heat and mass transfer through a porous medium had been given attention due to its applications in many engineering problems such as nuclear reactor design, geothermal systems, petroleum engineering applications, evaporation at the surface of a water body, control of pollutants in ground water, energy transfer in a wet cooling tower, food processing cooler [1] [2] , and the problem of heat and mass transfer flow of a laminar boundary layer over a stretching sheet in a saturated porous medium has an important application in the metallurgy and chemical engineering fields. Layek et al. [3] considered the effects of thermal radiation and variable fluid viscosity on free convective flow and heat transfer past a porous stretching surface while, Alharbi et al. [4] investigated the heat and mass transfer of MHD viscoelastic fluid flow through a porous medium over a stretching sheet with chemical reactions, due to the importance of Soret (Thermal-diffusion) and Dufour (Diffusion-thermo) effects on the fluids with very light molecular weight as well as medium molecular weight. Darcy’s empirical flow model represents a simple linear relationship between flow rate and pressure drop in a porous media; any deviation from the Darcy flow scenario is termed non-Darcy flow. Forchheimer [5] carried out a research on flowing of gas through coal beds and his report showed that the relationship between flow rate and potential gradient was non-linear at sufficiently high velocity and this non-linearity increased with flow rate. He added a second order velocity term to represent the microscopic inertial effect, and modified the Darcy equation into the Forchheimer equation, which was widely considered to describe the inertial effects due to additional friction observed for high velocity flow, Darcy [6] . Alam, et al. [7] , studied the effects of Dufour and Soret on a two-dimensional steady MHD free convective and mass transfer flow past a semi-infinite vertical porous plate in a porous medium numerically. Alam, et al. [8] furthered the research using Local similarity solution given by Scatter et al. [9] and Hashimoto [10] to transform the nonlinear partial equations governing the problem to lower order of coupled ordinary differential equation.
In all of the above mentioned studies, fluid viscosity and fluid thermal conductivity were assumed to be constant throughout the boundary layer. However, it is known that the physical properties of the fluid may change significantly with temperature. For lubricating fluids, heat generated by the internal friction and the corresponding rise in temperature affects the viscosity of the fluid and so the fluid viscosity can no longer be assumed constant. The increase of temperature leads to a local increase in the transport phenomena by reducing the viscosity across the momentum boundary layer and so the heat transfer rate at the wall is also affected greatly. External heating such as the ambient temperature and high shear rates can lead to a high temperature being generated within the fluid. This may have a significant effect on the fluid properties. It is a well known fact in fluid dynamics, that the property which is most sensitive to temperature rise is viscosity and thermal conductivity, Anyakoha, [11] . For instance, the viscosity of water decreases about 240% when the temperature increases from 10˚C to 50˚C. The viscosity of air is 0.6924 × 10−5 at 1000 K, 1.3289 at 2000 K, 2.286 at 4000 K and 3.625 at 8000 K as reported by Cebeci, et al. [12] . Mukhopadhyay [13] adopted Batchelor’s model of temperature dependent fluid viscosity when he studied the effect of radiation and variable fluid viscosity on flow and heat transfer along a symmetric wedge assuming constant thermal conductivity. Salem, et al. [14] investigated the effects of variable properties on MHD heat and mass transfer flow near a stagnation point towards a stretching sheet in a porous medium with thermal radiation and adopted the model of Prasad, et al. [15] for temperature dependent viscosity and thermal conductivity and also incorporated the stagnation point velocity into their momentum equation.
In this paper, we want to study the effects of variable fluid viscosity, variable thermal conductivity, Dufour and Soret on free convective heat and mass transfer of non-Darcian flow past a porous flat surface taking into account radiation effects using Rosseland approximation in modeling the radiative heat transfer.
2. Mathematical Formulation
A steady two-dimensional laminar free convection flow of viscous incompressible variable viscosity and variable thermal conductivity fluid along a porous vertical surface in the presence of suction and heat generation and absorption is considered. The governing mass, momentum, energy and concentration equations takes the form of [16]
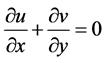 (1)
(1)
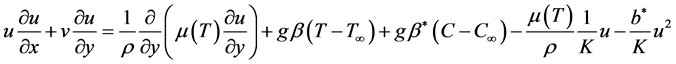 (2)
(2)
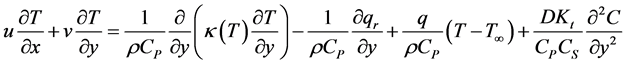 (3)
(3)
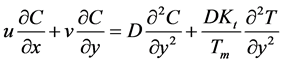 (4)
(4)
subject to the boundary conditions:
 (5)
(5)
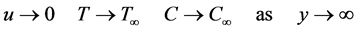 (6)
(6)
where x and y represents coordinate axes along the continuous surface in the direction of motion and perpendicular to it and  and v are the Darcian velocity components along x- and y-axis respectively,
and v are the Darcian velocity components along x- and y-axis respectively, 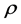 is the density, g is the force of gravity,
is the density, g is the force of gravity, 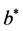 is the empirical constant,
is the empirical constant, 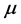 is the viscosity,
is the viscosity, 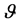 is the kinematic viscosity, BT is the coefficients of thermal expansion,
is the kinematic viscosity, BT is the coefficients of thermal expansion,  is the coefficient of volumetric expansion, K is the permeability of the porous medium,
is the coefficient of volumetric expansion, K is the permeability of the porous medium, 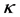 is the thermal conductivity, Cp is the specific heat at constant pressure, q is the dimensional heat absorption coefficient, C is the concentration,
is the thermal conductivity, Cp is the specific heat at constant pressure, q is the dimensional heat absorption coefficient, C is the concentration,  is the ambient concentration, Cp is the specific heat at constant pressure, Kt is the thermal diffusion ratio, Tm is the mean fluid temperature and Vw is the suction velocity across the stretching sheet. In this research, we consider variable viscosity, where the fluid viscosity
is the ambient concentration, Cp is the specific heat at constant pressure, Kt is the thermal diffusion ratio, Tm is the mean fluid temperature and Vw is the suction velocity across the stretching sheet. In this research, we consider variable viscosity, where the fluid viscosity 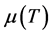 is assumed to vary as a linear function of temperature [16] and
is assumed to vary as a linear function of temperature [16] and 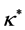 is the constant value of the coefficient of thermal conductivity far from the sheet and
is the constant value of the coefficient of thermal conductivity far from the sheet and 



Using Rosseland approximation for radiation

where σ is the Stefan-Boltzmann constant and 


Introducing stream functions,

Equations (2), (4), (5), (6) and (9) becomes



subject to


Introducing the following dimensionless variables,

Equations (10)-(14) reduce to a system of coupled nonlinear ordinary differential equations



subject to


3. Numerical Solution
The set of coupled ordinary differential Equations (16)-(18), subject to (19) and (20) was solved numerically using Runge-Kutta fourth order technique along with shooting method was implemented using MATLAB. The resultant initial value problem is solved by employing Runge-Kutta fourth order technique. The step size 



4. Results and Discussion
Figure 1 shows the velocity profiles for several values of 














5. Conclusion
In this paper, the effect of variable viscosity, thermal conductivity Dufour and Soret of non-Darcian flow on
Table 1. Effects of variation of ξ and ε.







Table 2. Effects of variation of FS.








Table 3. Effects of variation of Da.








Figure 1. Velocity profiles for several values of ξ and ε.
Figure 2. Temperature profiles for several values of ξ and ε.
Figure 3. Concentration profiles for several values of ξ and ε.
Figure 4. Velocity profiles for several values of Fs.
Figure 5. Temperature profiles for several values of Fs.
Figure 6. Concentration profiles for several values of Fs.
Figure 7. Velocity profiles for several values of local Darcy Da.
Figure 8. Temperature profiles for several values of local Darcy Da.
Figure 9. Concentration profiles for several values of local Darcy Da.
free convective heat and mass transfer past a porous flat plate was investigated using Runge-Kutta method with shooting method and Newton-Raphson technique. The procedure reveals accurately their effects and various solution branches. It is observed that with an increase in temperature-dependent fluid viscosity and thermal conductivity parameter, velocity increases, temperature decreases and concentration decreases across the flow region. Increasing Prandtl number as well as radiation parameter on the velocity boundary layer, reduces the velocity field, and decreases temperature with increasing value of thermal radiation, thereby causing concentration and Dufour to increase together with decrease in Soret parameter and slightly increases velocity. Our results and procedures can be used as an effective tool to investigate nonlinear boundary-problems in science and engineering.
Acknowledgements
Authors are thankful to the referee(s) for the valuable comments on the earlier draft of the paper.
References
- Ingham, D.B. and Pop, I. (2005) Transport Phenomena in Porous Medium III. Elsevier, Oxford.
- Vafai, K. (2005) Handbook of Porous Media. 2nd Edition, Taylor and Francis, New York.
- Layek, G.C. and Mukhopadhyay, S. (2008) Effects of Thermal Radiation and Variable Fluid Viscosity on Free Convective Flow and Heat Transfer past a Porous Stretching Surface. International Journal of Heat and Mass Transfer, 51, 2167-2178. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.11.038
- Alharbi-Saleh, M., Mohamed, A.A. and Mahmoud, S.E. (2010) Heat and Mass Transfer in MHD Visco-Elastic Fluid Flow through a Porous Medium over a Stretching Sheet with Chemical Reaction. Scientific Research, Applied Mathematics, 1, 446-445.
- Forchheimer, P.Z. (1901) Wasserbewegungdurch Boden. Zeitschrift des Vereins Deutscher Ingenieure, 45, 1781-1788.
- Darcy, H. (1856) Les fontainerpubligues de la ville de Dijoin. Dalmont.
- Alam, M.S. and Rahman, M.M. (2005) Dufour and Sorets on MHD Free Convective Heat and Mass Transfer Flow past a Vertical Flat Plate Embedded in a Porous Medium. Journal of Naval Architecture and Marine Engineering, 2, 55-65.
- Alam, M.S., Rahman, M.M. and Samad, M.A. (2006) Dufour and Soret Effects on Unsteady MHD Free Convective and Mass Transfer Flow past a Vertical Porous Plate in a Porous Medium. Nonlinear Analysis:Modeling and Control, 11, 217-226.
- Scatter, M.A. and Hossain, M.M. (1992) Unsteady Hydromagnetic Free Convection Flow with Hall Current and Mass Transfer along an Accelerated Porous Plate with Time-Dependent Temperature and Concentration. Canadian Journal of Physics, 70, 369-374. http://dx.doi.org/10.1139/p92-061
- Hashimoto, H. (1957) Boundary Layer Growth on a Flat Plate with Suction or Injection. Journal of the Physical Society of Japan, 12, 68-72. http://dx.doi.org/10.1143/JPSJ.12.68
- Anyakoha, M.W. (2010) New School Physics. 3rd Edition, Africana First Publisher, Enugu, 36-51.
- Cebeci, T. and Bradshaw, P. (1984) Physical and Computational Aspects of Convective Heat Transfer. Springer, New York. http://dx.doi.org/10.1007/978-3-662-02411-9
- Mukhopadhyay, S. (2009) Effects of Radiation and Variable Fluid Viscosity on Flow and Heat Transfer along a Symmetric Wedge. Journal of Applied Fluid Mechanics, 2, 29-34.
- Salem, A.M. and Fathy, R. (2012) Effects of Variable Properties on MHD Heat and Mass Transfer Flow near a Stagnation Point towards a Stretching Sheet in a Porous Medium with Thermal Radiation. Chinese Physics B, 21, Article ID: 054701.
- Prasad, K.V., Vajravelu, K. and Datti, P.S. (2010) The Effects of Variable Fluid Properties on the Hydromagnetic Flow and Heat Transfer over a Non-Linearly Stretching Sheet. International Journal of Thermal Sciences, 49, 603-610. http://dx.doi.org/10.1016/j.ijthermalsci.2009.08.005
- Batchelor, G.K. (1987) An Introduction to Fluid Dynamics. Cambridge University Press, London.
- Loganathan, P. and Arasu, P.P. (2010) Lie Group Analysis for the Effects of Variable Fluid Viscosity and Thermal Radiation on Free Convective Heat and Mass Transfer with Variable Stream Condition. Scientific Research Journal, 2, 625-634. http://dx.doi.org/10.4236/eng.2010.28080











