American Journal of Computational Mathematics
Vol.2 No.3(2012), Article ID:23200,5 pages DOI:10.4236/ajcm.2012.23029
Plane Stagnation Double-Diffusive MHD Convective Flow with Convective Boundary Condition in a Porous Media
1Department of Mathematical Sciences, Ondo State University of Science and Technology, Okitipupa, Nigeria
2Department of Mathematics, Statistics and Computer Science, Kaduna Polytechnic, Kaduna, Nigeria
Email: okedayo@yahoo.com
Received May 9, 2012; revised June 27, 2012; accepted July 5, 2012
Keywords: Plane Stagnation; Double-Diffusive; MHD Convective Flow and Porous Media
ABSTRACT
A numerical analysis has been carried out to study the problem of plane stagnation double-diffusive MHD convective flow with convective boundary condition in a porous media. The governing nonlinear partial differential equations have been reduced to systems of nonlinear ordinary differential equations by the similarity transformations. The transformed equations are solved numerically by using the classical fourth order Runge-Kutta method together with the shooting technique implemented on a computer program. The effects of the physical parameters are examined on the velocity, temperature and concentration profiles. Numerical data for the skin-friction coefficients, Nusselt and Sherwood numbers have been tabulated for various parametric conditions and are also shown graphically and discussed.
1. Introduction
The effect of free convection on the flow of a viscous incompressible fluid past a plane stagnation point on an infinite vertical plate has many important scientific and technological applications in the astrophysical, geophysical and engineering problems. The heating of rooms and buildings by the use of radiators is a familiar example of heat transfer by convection. Heat and mass transfer play an important role in manufacturing industries for the design of fins, steel rolling, nuclear power plants, gas turbines and various propulsion device for aircraft, combustion and furnace design, materials processing, energy utilization, temperature measurements. Most studies have been concerned with constant surface velocity and temperature, but for many practical applications the surface undergoes convective cooling or heating.
The growing interest in the field of flow through porous media stems from the fact that heat and mass transfer through porous media occurs in many engineering, geophysical and biological applications. Convection flows in porous media are particularly important in environmental studies involving air and water pollution. In order to assess the impact of an emission source, it is necessary to predict both the trajectory and the diffusion of the plum or jet at several distances away from the source. In practice, most emissions of a buoyant effluent are accompanied by a discharge momentum flux, hence the need to study the combined effect of heat and mass transfer in a buoyant driven flow.
The subject of Magneto hydrodynamics has attracted the attention of a large number of scientists due to its diverse application. In astrophysics and geophysics, it is applied to study the stellar and solar structures, interstellar matter and radio propagation through the ionosphere. In engineering, it finds its application in MHD pumps and MHD bearing. The study of effects of magnetic field on free convection flow is important in liquid metals, electrolytes, and ionized gases. At the high temperature attained in some engineering devices, gas, for example, can become ionized and so becomes an electrical conductor. The ionized gas or plasma can be made to interact with the magnetic field and alter heat transfer and friction characteristic. Recently, it is of great interest to study the effect of magnetic field on the temperature distribution and heat transfer when the fluid is not only an electrical conductor but also when it is capable of emitting and absorbing thermal radiation.
Heat transfer characteristics in stagnation point flow has also been studied by several authors, for example Hiemenz [1] studied the two dimensional flow of an incompressible viscous fluid, Attia [2] studied the MHD stagnation point flow with heat transfer over a permeable surface, Massoudi and Ramezan [3] carried out an analysis of the boundary layers heat transfer of a viscoelastic fluid at a stagnation point. While Chiam [4] studied the heat transfer with variable conductivity in a stagnation point flow towards a stretching sheet. On the MHD stagnation point flow, several works has been published which include the papers of Ariel [5], Chamkha [6] and Attia [7].
Heat and mass transfer play an important role in manufacturing industries for the design of fins, steel rolling, nuclear power plants, gas turbines and various propulsion device for aircraft, combustion and furnace design, materials processing, energy utilization, temperature measurements. Most studies have been concerned with constant surface velocity and temperature, but for many practical applications the surface undergoes stretching and cooling or heating that cause surface velocity and temperature variations. Crane [8], Velggaar [9], and Gupta [10] have analyzed the stretching problem with a constant surface temperature, while Soundalgekar and Ramana [11] have investigated the constant surface velocity case with a power-law temperature variation. Grubka and Bobba [12] have analyzed the stretching problem for a surface moving with a linear velocity and with a variable surface temperature.
The problem of plane stagnation double diffusive convective flow with convective boundary conditions in a porous media has receive little or no attention by researchers hence the motivation for this study.
2. Mathematical Formulations
A two-dimensional body is placed in a stream of quiescent fluid. We consider heat transfer near the upstream stagnation line, where the flow is assumed to be laminar. The problem is restricted to the case of a plane plate perpendicular to the stream. It is assumed that the fluid properties are constant except for the fluid viscosity which vary as an inverse linear function of temperature as follows.
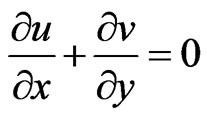 (1)
(1)
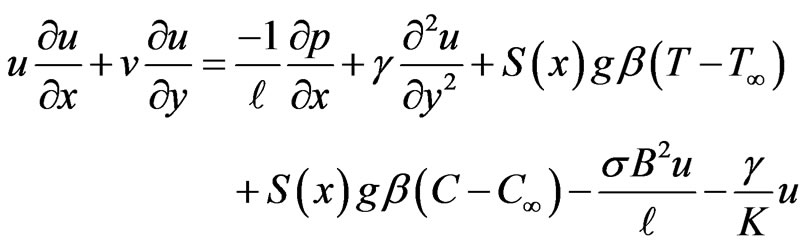 (2)
(2)
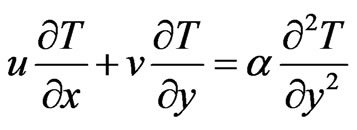 (3)
(3)
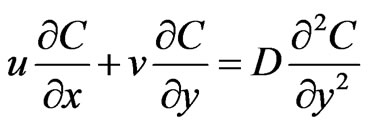 (4)
(4)
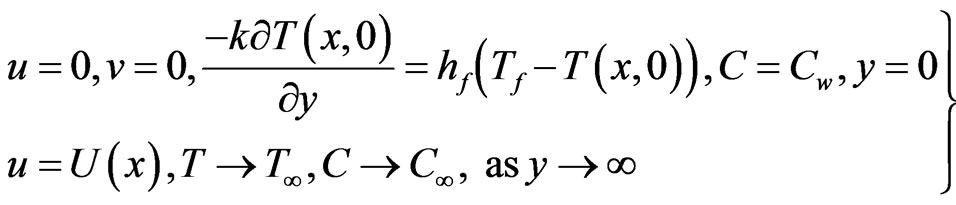 (5)
(5)
where u and v are the velocity components in the x and y directions respectively, T is the temperature, 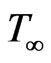 is the free stream temperature,
is the free stream temperature, 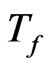 is the reference temperature,
is the reference temperature, 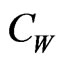 is the reference concentration and
is the reference concentration and 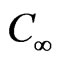 is the free stream concentration. g is the acceleration due to gravity,
is the free stream concentration. g is the acceleration due to gravity, 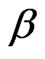 is the coefficient of expansivity, D is the molecular diffusion coefficient, C is the mass concentration, is the free stream temperature, is the free stream concentration, U(x) is the free stream velocity and S(x) is the body force, K is the permeability, p is the pressure, B is the magnetic field,
is the coefficient of expansivity, D is the molecular diffusion coefficient, C is the mass concentration, is the free stream temperature, is the free stream concentration, U(x) is the free stream velocity and S(x) is the body force, K is the permeability, p is the pressure, B is the magnetic field, 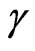 is the kinematic viscosity,
is the kinematic viscosity, 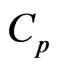 is the specific heat capacity,
is the specific heat capacity, 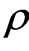 is the fluid density,
is the fluid density,  is the electrical conductivity,
is the electrical conductivity, 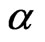 is the thermal diffusivity.
is the thermal diffusivity.
In order to solve Equations (1)-(5) above we introduce the following dimensionless quantities.
 (4a)
(4a)
Substituting the above variables in Equation (4a) into Equations (1)-(4), we obtain
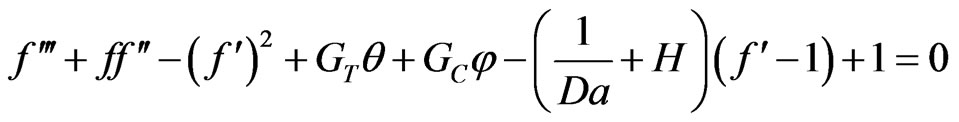 (5)
(5)
 (6)
(6)
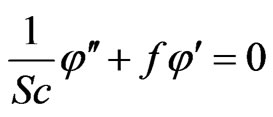 (7)
(7)
Subject to
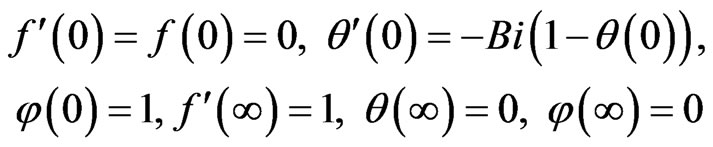 (8)
(8)
where GT is the Grashof number, GC is the solutal Grashof number, Sc is the Schmidt number, Pr is the Prandtl number, H is the magnetic parameter, Da is the Darcy number, and Bi is the Biot number. And prime denote differentiation with respect to η.
3. Numerical Results and Discussion
The formulation of the problem that account for, the plane stagnation double diffusive convective flow with convective boundary conditions in a porous media was accomplished. The nonlinear Equations (5)-(8) are solved numerically using the classical fourth order Runge-Kutta method together with the shooting technique implemented on a computer program written in Maple (14). A convenient step size was chosen to obtain the desired accuracy. The values for the velocity, temperature, concentration profiles and the skin-friction coefficients, Nusselt and Sherwood numbers have been obtain and tabulated for various parametric conditions, as presented in Table 1.
In Figure 1, the typical velocity profiles in the boundary layer for various values of the thermal Grashof number Gt, was shown. It is observed that the more the thermal Grashof number Gt, it ieads to rise in the velocity because of enhancement in the buoyancy force. It was also noticed that the velocity increases rapidly near the wall of the porous plate as the Grashof number increases and then decreases to the free stream velocity.
Different values of the Solutal Grashof number, velocity profiles in the boundary layer are shown in Figure 2. The velocity distribution attains a peak value in the vicinity of the plate and then decreases to approach a free stream value. The fluid velocity increases and the peak value becomes more distinctive due to increase in the buoyancy force represented by the Solutal Grashof number.
Figure 3 illustrates the influence of the Darcy number on the velocity profiles. It indicates the velocity profiles showing the effect of Darcy number. It can be seen that velocity profiles increase with the increase of Darcy number. Hence, as Darcy number increases the velocity increases.
The effect of Hartmann number on the velocity profiles is shown in Figure 4. It is observed that an increase in the Hartmann number results in a decrease of the average velocity within the boundary layer.
The temperature profile for different values of the Prandtl number is shown in Figure 5. It is observed that an increase in the Prandtl number, results a decrease of the temperature within the boundary layer.
The Temperature profiles for various values of the Biot number is depicted in Figure 6. It is clearly seen that the temperature increases with the increase of the Biot number.
Figure 7 shows the effect of different values of the Schmidt number on Concentration profiles. As the
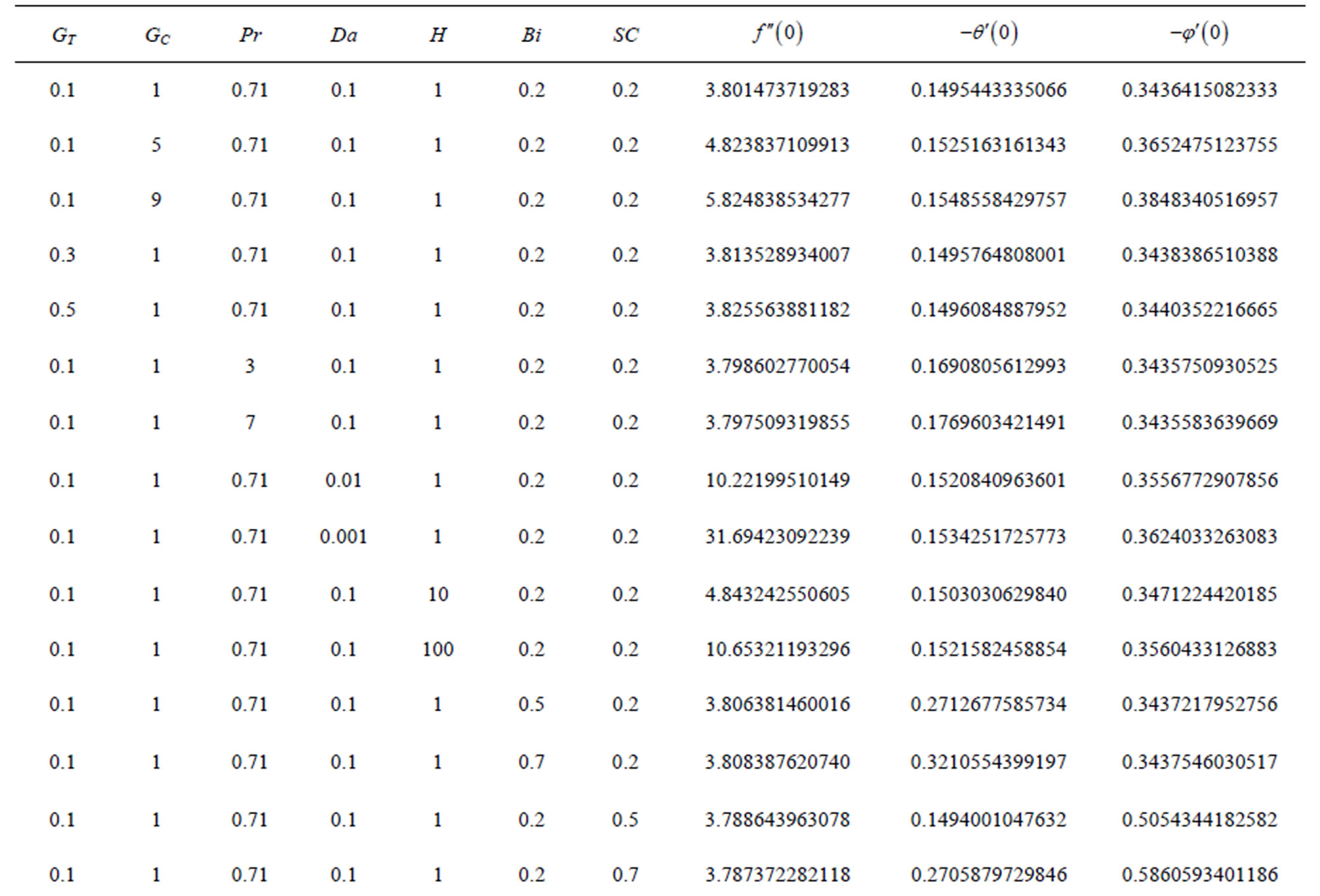
Table 1. Skin friction coefficient, Nusselt and Sherwood numbers for the various thermo-physical parameters.
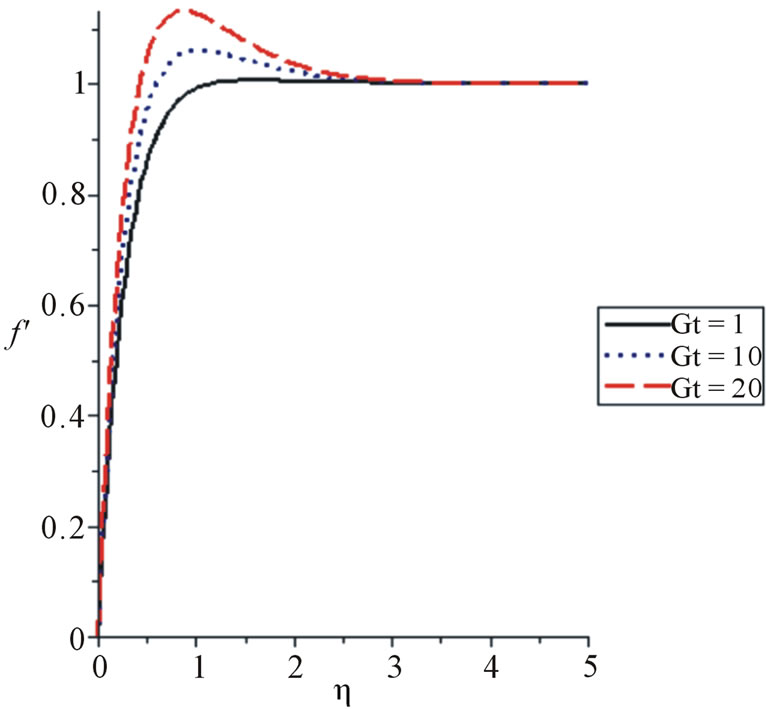
Figure 1. Velocity profile for various values of the thermal Grashof number for Gc = 0.1, Da = 0.1, H = 1, Pr = 0.71, Bi = 0.2, Sc = 0.2.

Figure 2. Velocity profile for various values of the solutal Grashof number for Gt = 0.1, Da = 0.1, H = 1, Pr = 0.71, Bi = 0.2, Sc = 0.2.
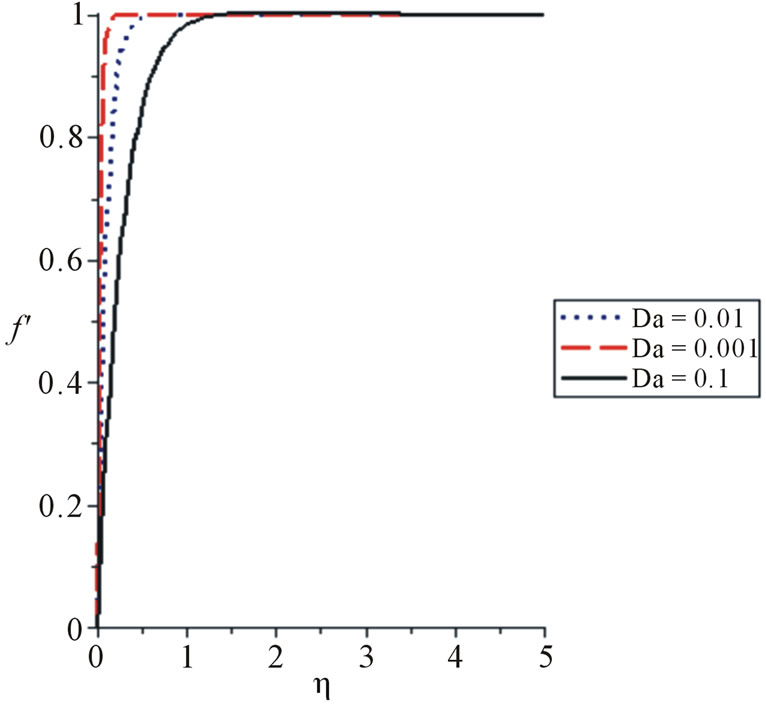
Figure 3. Velocity profile for various values of the Darcy number for Gt = 0.1, Gc = 0.1, H = 1, Pr = 0.71, Bi = 0.2, Sc = 0.2.
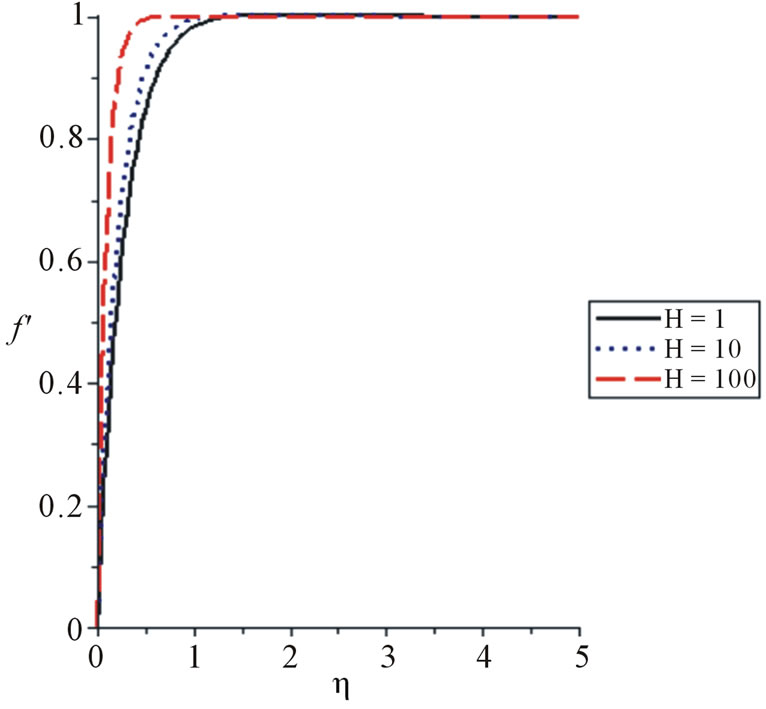
Figure 4. Velocity profile for various values of the Hartmann number for Gt = 0.1, Da = 0.1, Gc = 0.1, Pr = 0.71, Bi = 0.2, Sc = 0.2.

Figure 5. Temperature profile for various values of the Prandtl number for Gt = 0.1, Da = 0.1, H = 1, Gc = 0.1, Bi = 0.2, Sc = 0.2.

Figure 6. Temperature profile for various values of the Biot number for Gt = 0.1, Da = 0.1, H = 1, Pr = 0.71, Gc = 0.1, Sc = 0.2.
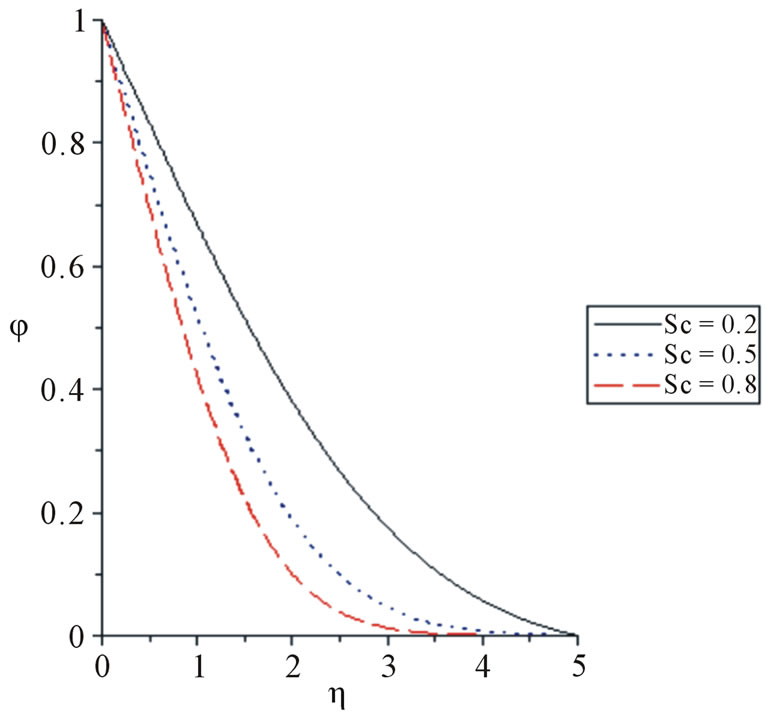
Figure 7. Concentration profile for various values of the Schmidt number for Gt = 0.1, Da = 0.1, H = 1, Pr = 0.71, Bi = 0.2, Sc = 0.2, Gc = 0.1.
Schmidt number increases the concentration decreases, which makes the concentration buoyancy effects to decrease resulting into a reduction in the fluid velocity.
REFERENCES
- K. Hiemenz, “The Boundary Layer on a Circular Cylinder in Uniform Flow (in German),” Dingl. Polytec. J., Vol. 326, 1911, pp. 321-328.
- H. A. Attia, “Hydrodynamic Stagnation Point Flow with Heat Transfer over a Permeable Surface,” Arabian Journal for Science and Engineering, Vol. 28, 2003, pp. 107- 112.
- M. Massoudi and M. Ramezan, “Boundary Layers Heat Transfer Analysis of a Viscoelastic Fluid at a Stagnation Point,” Proceedings of the ASME Heat Transfer Division, Vol. 130, 1990, pp. 81-86.
- T. C. Chiam, “Magnetohydrodynamic Heat Transfer over a Non-Isothermal Stretching Sheet,” Acta Mecanica, Vol. 122, No. 1-4, 1997, pp. 169-179.
- P. D. Ariel, “Hiemenz Flow in Hydromagnetics,” Acta Mechanica, Vol. 103, No. 1-4, 1994, pp. 31-43. doi:10.1007/BF01180216
- A. J. Chamkha, “Hydromagnetic Plane and Axisymmetric Flow near a Stagnation Point with Heat Transfer,” International Communications in Heat and Mass Transfer, Vol. 25, No. 2, 1998, pp. 269-278. doi:10.1016/S0735-1933(98)00014-1
- H. A. Attia, “Hydrodynamic Stagnation Point Flow with Heat Transfer over a Permeable Surface,” Arabian Journal for Science and Engineering, Vo. 28, 2003, pp. 107- 112.
- L. J. Crane, “Flow Past a Stretching Plate,” Zeitschrift Für Angewandte Mathematik Und Physik (Zamp), Vol. 21, No. 4, 1970, pp. 645-647.
- J. Vleggaar, “Laminar Boundary-Layer Behavior on Continuous, Accelerating Surfaces,” Chemical Engineering Science, Vol. 32, No. 12, pp. 1517-1525. doi:10.1016/0009-2509(77)80249-2
- P. S. Gupta and A. S. Gupta, “Heat and Mass Transfer on a Stretching Sheet with Suction or Blowing,” The Canadian Journal of Chemical Engineering, Vol. 55, No. 6, 1977, pp. 744-746.
- V. M. Soundalgekar and T. V. Ramana Murty, “Heat Transfer Past a Continuous Moving Plate with Variable Temperature,” Heat and Mass Transfer, Vol. 14, No. 2, 1980, pp. 91-93. doi:10.1007/BF01806474
- L. J. Grubka and K. M. Bobba, “Heat Transfer Characteristics of a Continuous, Stretching Surface with Variable Temperature,” Journal of Heat Transfer, Vol. 107, No. 1, 1985, pp. 248-250. doi:10.1115/1.3247387

