American Journal of Computational Mathematics
Vol.2 No.2(2012), Article ID:20093,7 pages DOI:10.4236/ajcm.2012.22016
One Approach to Construction of Bilateral Approximations Methods for Solution of Nonlinear Eigenvalue Problems
Institute of Applied Problems of Mechanics & Mathematics, National Academy of Sciences of Ukraine, Lviv, Ukraine
Email: podlev@iapmm.lviv.ua
Received December 28, 2011; revised February 8, 2012; accepted February 15, 2012
Keywords: Nonlinear Eigenvalue Problem; Derivatives of Matrix Determinant; Numerical Algorithm of Alternate Approximations
ABSTRACT
In this paper a new approach to construction of iterative methods of bilateral approximations of eigenvalue is proposed and investigated. The conditions on initial approximation, which ensure the convergence of iterative processes, are obtained.
1. Introduction
Many theoretical and applied problems of mathematical physics, mechanics and engineering sciences lead to eigenvalue problems. The class of self-adjoint eigenvalue problems, perhaps the most important class of problems because numerous problems that occur in practice belong to this class. However, the eigenvalue problems that are important in practice, very rarely can be solved in a closed form, as a rule one must use numerical methods to solve them. Most numerical methods simply provide approximations to eigenvalues, but they do not make it possible to state how far the calculated eigenvalue is from the true one. Since the self-adjoint eigenvalue problem can have only real eigenvalues, the problem of obtaining approximations and corresponding error estimations of approximation accuracy is equivalent to the determination of upper and lower bounds for the eigenvalues.
Large interest in the eigenvalue bounds, take not only mathematicians, but also physicists, chemists, and engineers and it has many reasons. We name at least two of them here:
1) Lower bounds for eigenvalues are necessary in order to compare predictions of physical theories with experimental results; fine structure corrections in quantum mechanical problems.
2) The knowledge of boundaries for eigenvalues makes it possible in many cases to estimate the reliability of iterative approximation, that is at every step of iterative process to obtain the comfortable a posteriori estimate of error calculations.
For a large class of problems, good upper bounds for positive eigenvalues can be determined relatively easy by means of the Rayleigh-Ritz procedure. To estimate the accuracy of approximations, which are obtained by the Rayleigh-Ritz method, it is important to know at least rough approximations from below. Basically, there are three classes of methods for calculation the lower bounds for eigenvalues (disregarding the methods with a very limited scope of application):
1) The methods based on inclusion theorem.
2) The method of intermediate problems.
3) The Fichera method.
The methods based on inclusion theorems go back to G. Temple [1], L. Collatz [2], and N.J. Lehmann [3,4]. For these methods we need of rough a priori information on the localization of one of the eigenvalues, for example, we need to know: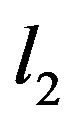 —the lower bound of
—the lower bound of  and
and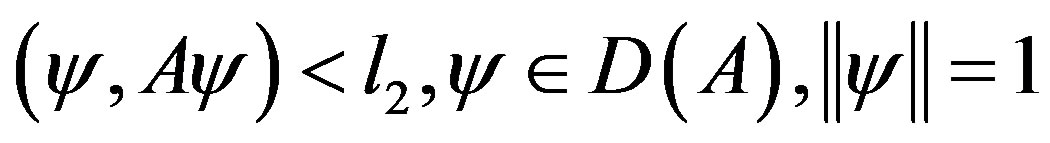 , then
, then
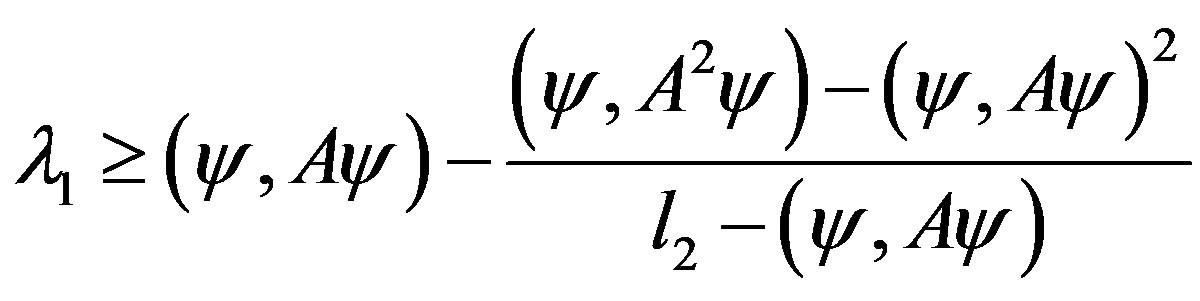 .
.
In this direction we should note the work of A. V. Knyazev [5,6], B. N. Parlett [7], Behnke H. [8,9], Marmorino M.G. [10].
The method of intermediate problems was proposed by A. Weinstein [11]. Later on the method has been refined by N. Bazly, D. W. Fox, C. Beattie, and others (see [12- 14] and the bibliography in [10,14,15]). For this method one needs the eigenvectors of a neighbouring eigenvalue problem in a closed form. The essence of the method of intermediate problems is as follows: along with the selfadjoint operator  whose eigenvalues are sought, the operator
whose eigenvalues are sought, the operator 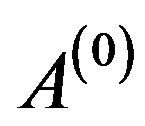 with known eigenvalues and eigenvectors, and such that the operator
with known eigenvalues and eigenvectors, and such that the operator 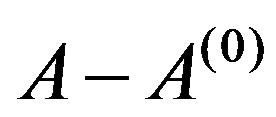 is positive, is considered.
is positive, is considered. 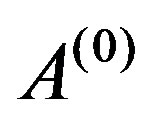 is called a basic operator. Its range probably lies below the spectrum of the operator
is called a basic operator. Its range probably lies below the spectrum of the operator . Once the basic operator is selected, by means of the finite perturbation
. Once the basic operator is selected, by means of the finite perturbation  a monotonous sequence of intermediate operators
a monotonous sequence of intermediate operators 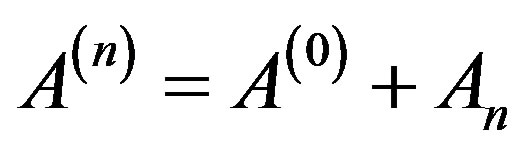 spectra of which approximate the spectrum of operator
spectra of which approximate the spectrum of operator  from below is constructed.
from below is constructed.
The method, different from the method of intermediate problems was proposed by G. Fichera [16]. This method does not require constructing a base operator with a known spectrum, but has a narrower scope of application. It is applied to the operator , the inverse to which is a compact operator, and the problem
, the inverse to which is a compact operator, and the problem , where
, where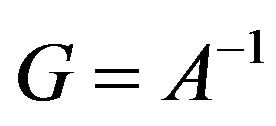 ,
, 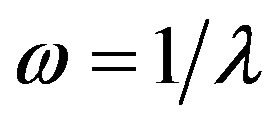 , is solved. Then
, is solved. Then
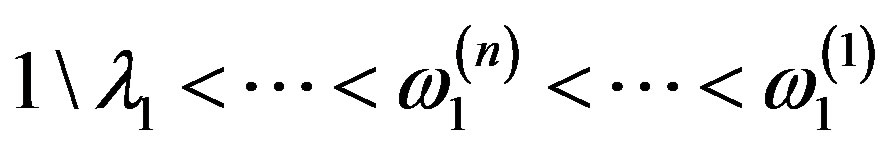 .
.
This paper presents a new approach to construction the methods and algorithms of bilateral approximations of eigenvalues for nonlinear (with respect to spectral parameter) eigenvalue problems, wich have supra-linear speed of convergence. This approach does not use the concepts and apparatus of interval analysis (see, e.g. [20, 21]).
The idea of the approach proposed is that for a continuous monotone in a neighborhood of simple zero  function
function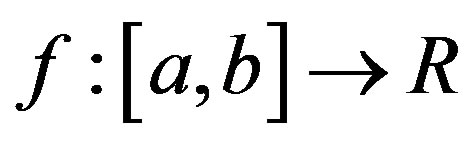 , which describes the nonlinear equation some auxiliary function
, which describes the nonlinear equation some auxiliary function 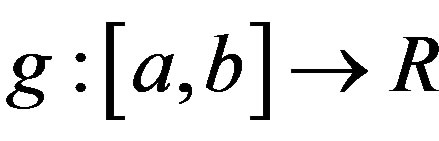 that has the same zero as the function
that has the same zero as the function 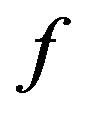 and such necessary properties that allow one to build the iterative processes which give monotonous bilateral (alternating or including) approximations to the root of a nonlinear equation [17-19] is constructed and investigated.
and such necessary properties that allow one to build the iterative processes which give monotonous bilateral (alternating or including) approximations to the root of a nonlinear equation [17-19] is constructed and investigated.
Within this approach, the algorithms of bilateral analogues of Newton’s method for finding the eigenvalues of nonlinear spectral problems are constructed and justified. The conditions on the initial approximations which provide the alternate approximations to the eigenvalue from two sides and ensure the convergence of iterative process, are obtained.
2. Statement of the Problem and Some Preliminary Results
We consider the nonlinear eigenvalue problem
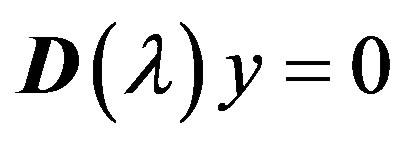 , (1)
, (1)
where 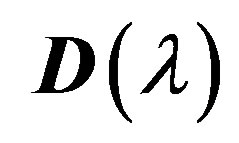 is a square matrix of order
is a square matrix of order , all elements of which are sufficiently smooth (at least twice continuously differentiable) functions of the parameter
, all elements of which are sufficiently smooth (at least twice continuously differentiable) functions of the parameter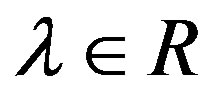 ,
,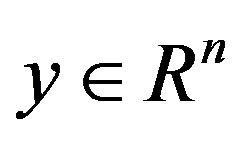 . Eigenvalues sought for solutions of the determinant equation
. Eigenvalues sought for solutions of the determinant equation
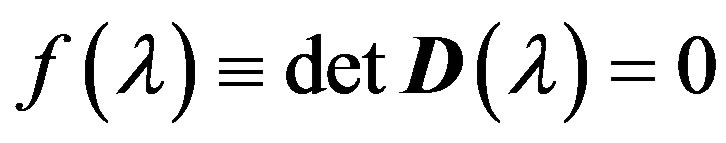 . (2)
. (2)
To determine the isolated eigenvalue of matrix we propose and justify the Newton-type iterative processes that give the alternate approximations to the root of the Equation (2), i.e.
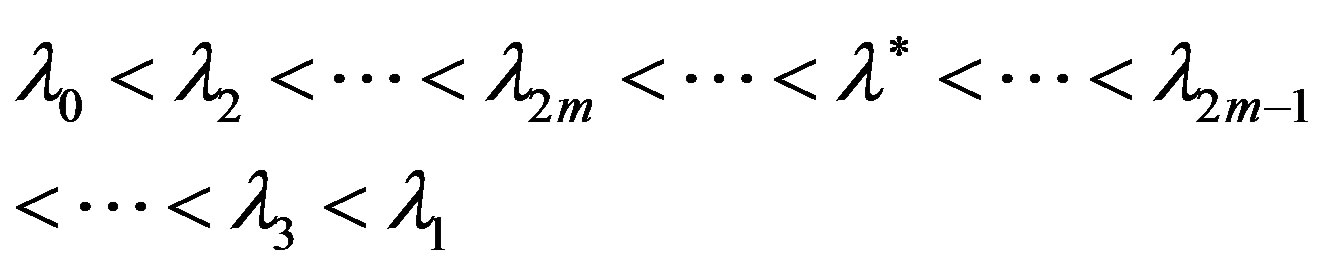 (3)
(3)
or

and the including monotonous bilateral approximations to the root, i.e.
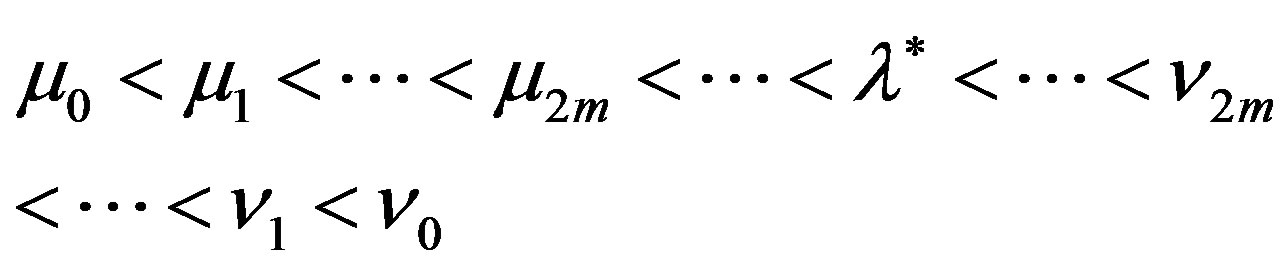 (4)
(4)
without revealing in so doing the determinant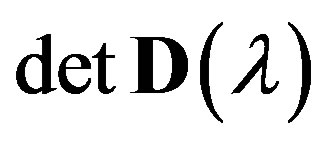 . This means that the left hand side of equation (2) in explicit form is not set, but the algorithm of finding the functions
. This means that the left hand side of equation (2) in explicit form is not set, but the algorithm of finding the functions  and thein derivatives
and thein derivatives 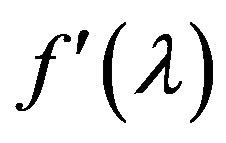 and
and 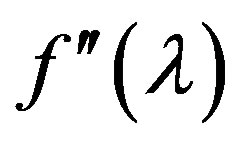 at a fixed value of the parameter
at a fixed value of the parameter , using the LU-decomposition of the matrix
, using the LU-decomposition of the matrix 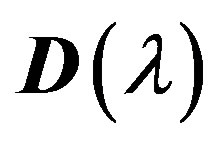 is proposed. This algorithm is based on the fact that the matrix
is proposed. This algorithm is based on the fact that the matrix 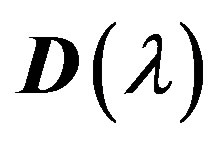 of the order
of the order , in which at any given value
, in which at any given value  the principal minors of all orders from 1 to
the principal minors of all orders from 1 to  differ from zero, by LU-decomposition can be written as
differ from zero, by LU-decomposition can be written as
 where
where 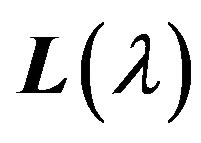 is the lower triangular matrix with single diagonal elements, and
is the lower triangular matrix with single diagonal elements, and 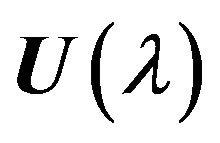 is the upper triangular matrix. Then
is the upper triangular matrix. Then
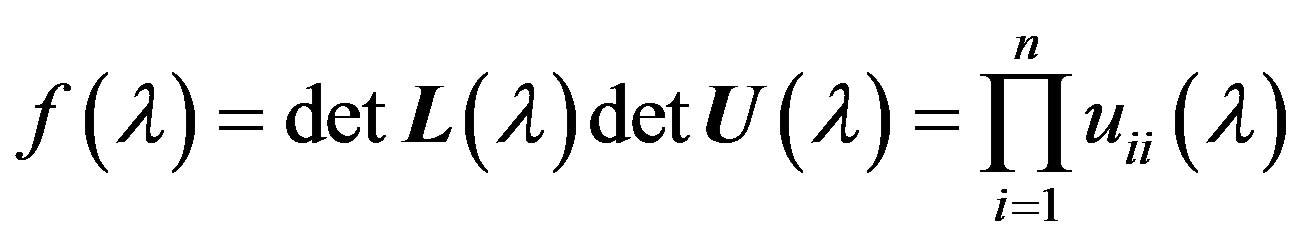
Since the elements of a square matrix 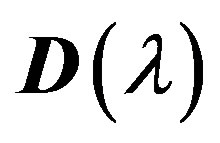 (and, therefore, the matrix
(and, therefore, the matrix ) are differentiable function, with respect to
) are differentiable function, with respect to , then for any
, then for any  we obtain that
we obtain that
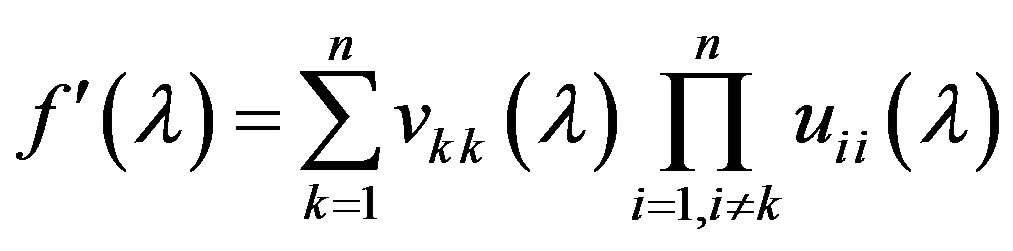 ,
,
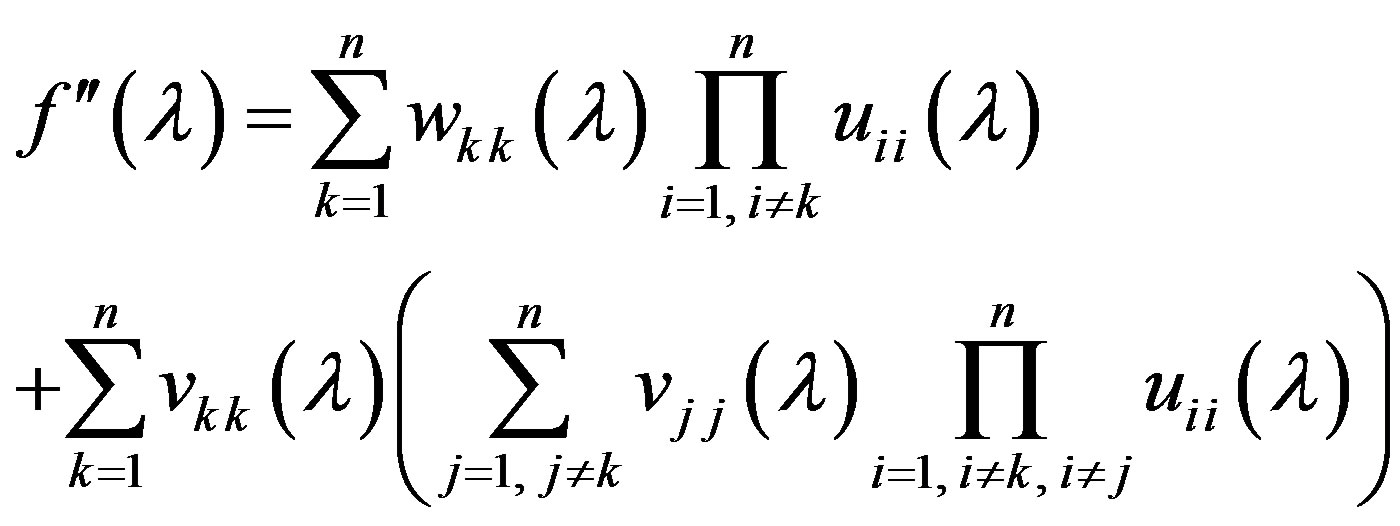
where 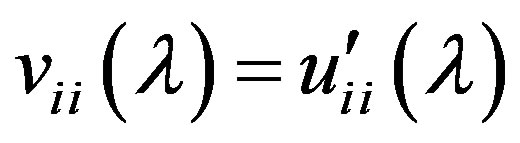 and
and 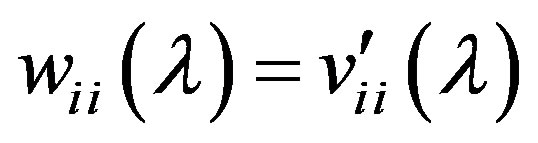 are the elements of matrices
are the elements of matrices 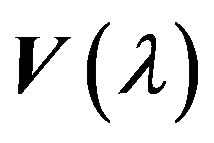 and
and 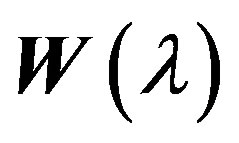 in such decompositions
in such decompositions
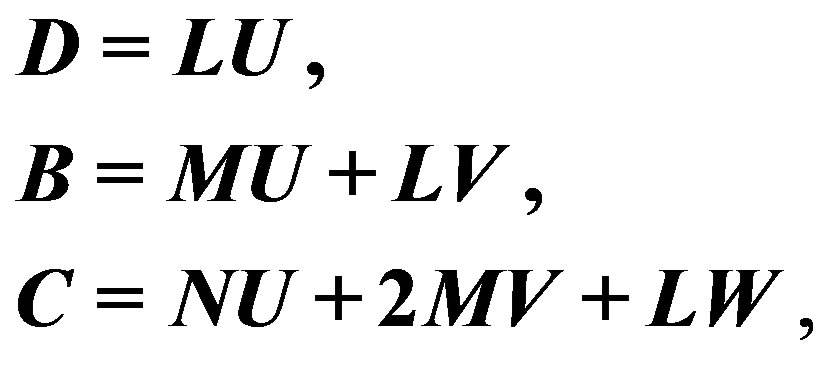 (5)
(5)
whence we obtain
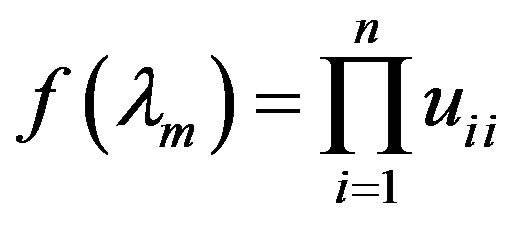 ,
, 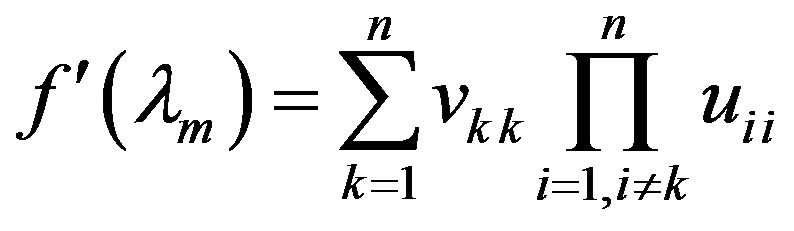 ,
,
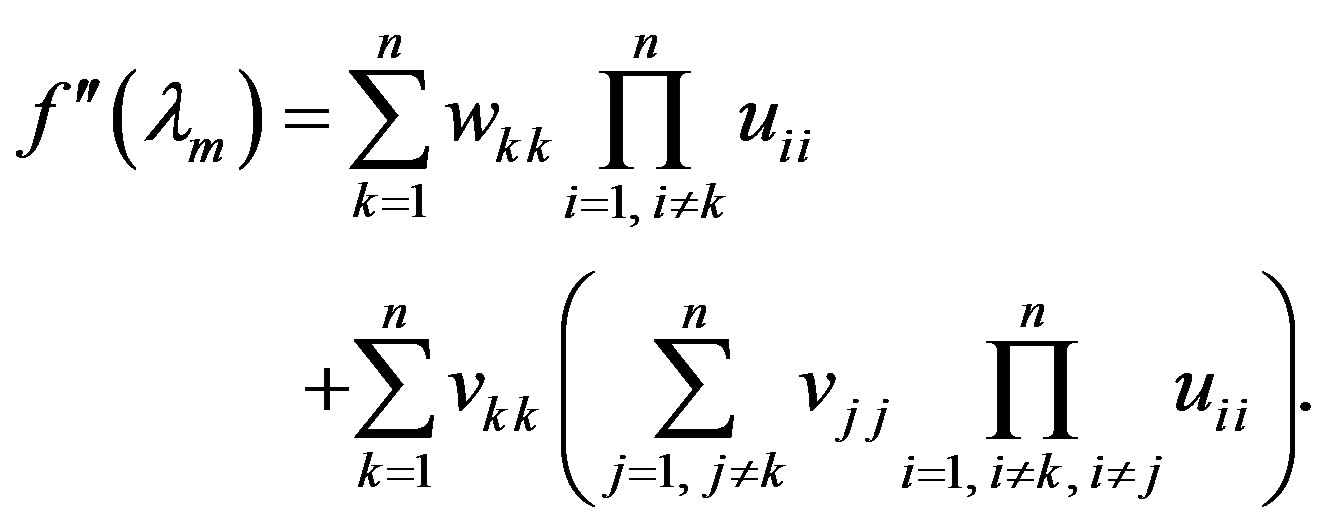 (6)
(6)
The elements of matrices in the decompositions (5) can be calculated using the corresponding recurrent relations written out in [22] (see also [23,24]).
So, not knowing the explicit dependence 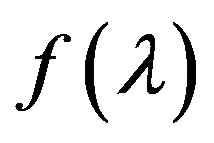 on
on , for any fixed
, for any fixed  we can find the value of
we can find the value of 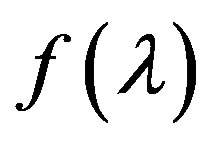 and its derivatives. Therefore, for solving (2) we can use the methods that apply the derivatives, in particular, to construct the Newton-type methods, which give the bilateral approximation to the solution. This requires further study of the function
and its derivatives. Therefore, for solving (2) we can use the methods that apply the derivatives, in particular, to construct the Newton-type methods, which give the bilateral approximation to the solution. This requires further study of the function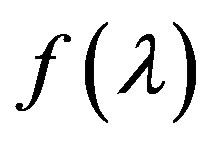 , which are realized later in the work.
, which are realized later in the work.
Further, we demand 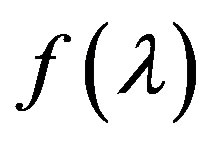 to be a three times continuously differentiable function of real variable. By
to be a three times continuously differentiable function of real variable. By 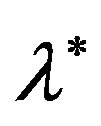 we denote an accurate simple root of equation (2) (
we denote an accurate simple root of equation (2) ( =0), in some neighborhood of which such behavior of function
=0), in some neighborhood of which such behavior of function 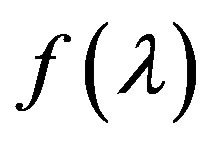 is possible.
is possible.
1). Function  is convex (
is convex (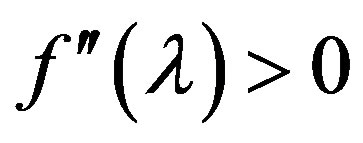 ) and its derivative is
) and its derivative is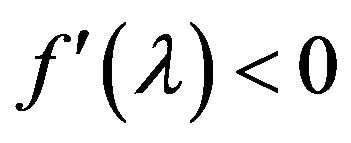 .
.
2). Function  is concave (
is concave (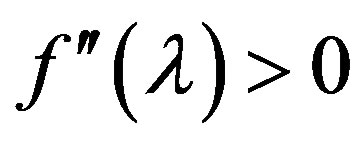 ) and its derivative is
) and its derivative is .
.
3). Function 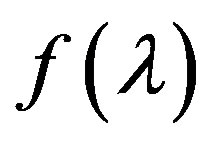 is convex (
is convex (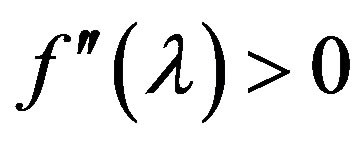 ) and its derivative is
) and its derivative is .
.
4). Function 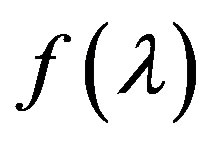 is concave (
is concave (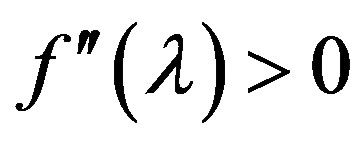 ) and its derivative is
) and its derivative is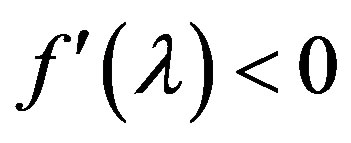 .
.
3. Auxiliary Function and Its Properties
Along with  we consider also a function
we consider also a function
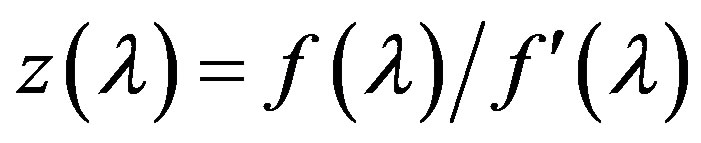 which obviously has the same zeros as the function
which obviously has the same zeros as the function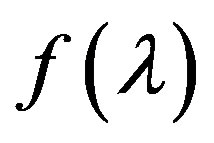 . It is easy to verify that
. It is easy to verify that  is twice constinuously differentiable at the point of
is twice constinuously differentiable at the point of  for which the relation
for which the relation
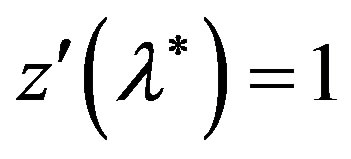 ,
, 
is satisfied and which has the following properties.
Theorem 3.1. Let 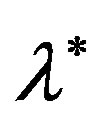 be a simple real root of Equation (2) in some neighborhood
be a simple real root of Equation (2) in some neighborhood  of which for the function
of which for the function 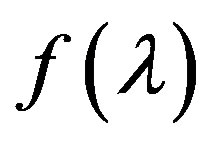 one of the conditions (A)-(D) is satisfied. Then there is a neighborhood of the root
one of the conditions (A)-(D) is satisfied. Then there is a neighborhood of the root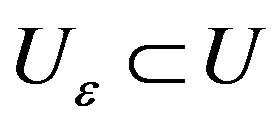 , in which:
, in which:
1) when the condition (A) or (D) is satisfied, the function 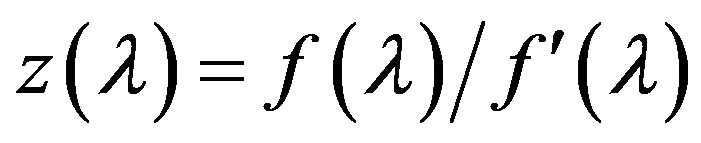 is a convex and monotonically increasing function, its derivative
is a convex and monotonically increasing function, its derivative 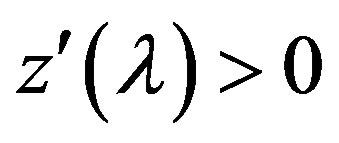 and it increases monotonically;
and it increases monotonically;
2) when the condition (B) or (C) is satisfied, the function 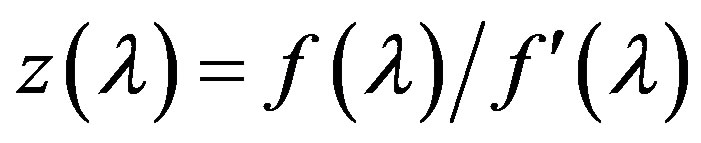 is a concave and monotonically increasing function, its derivative
is a concave and monotonically increasing function, its derivative 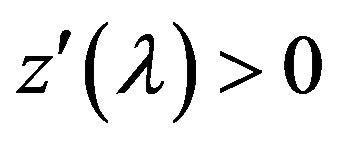 and it monotonically decreases.
and it monotonically decreases.
Proof. Let  be a decreasing and convex with respect to
be a decreasing and convex with respect to  on U function, that is,
on U function, that is, 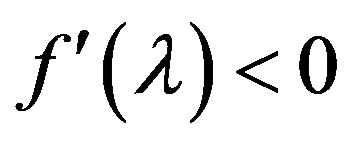 and
and 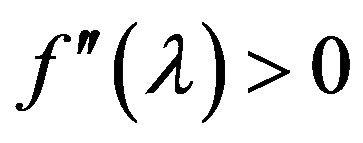 (the case (A)).
(the case (A)).
Since the function
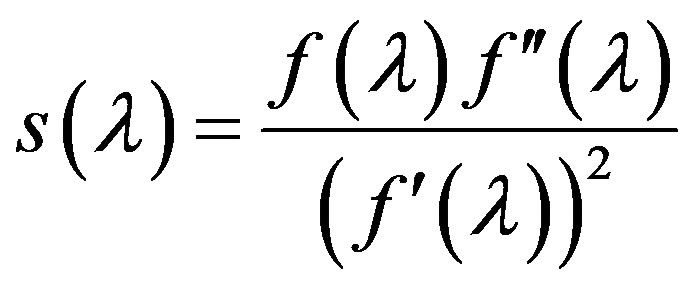
at the point 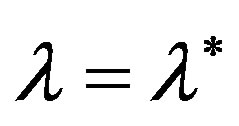 is equal to zero, then because of continuity of
is equal to zero, then because of continuity of 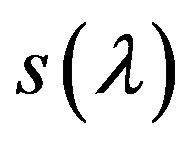 there is such neighborhood of the root
there is such neighborhood of the root
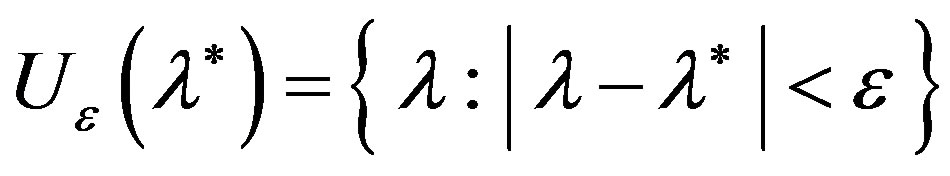 in which
in which
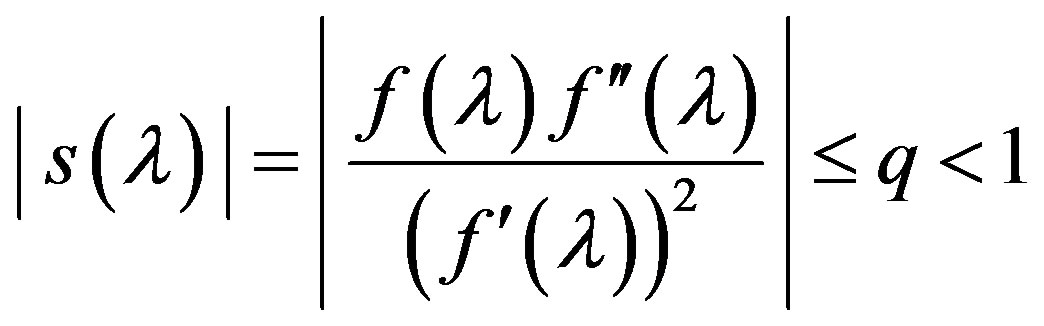 .
.
It follows that in the neighborhood 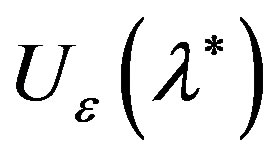 the function is
the function is , since
, since
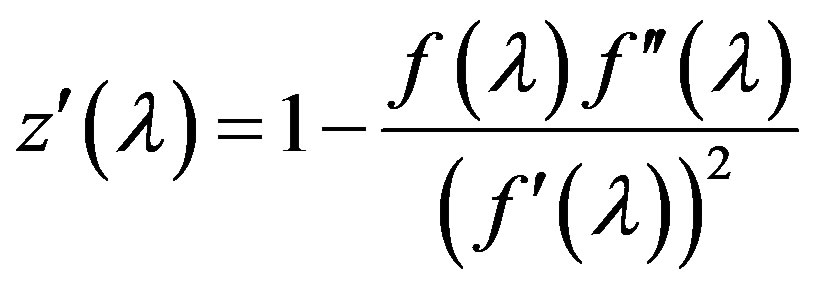 . (7)
. (7)
Now from the mean value theorem, applied to differentiable functions 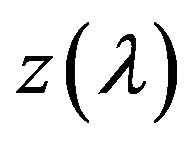 on the interval
on the interval 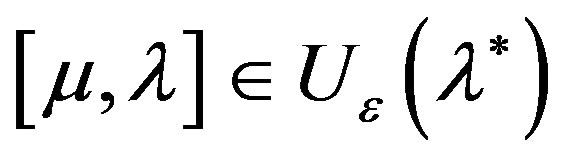 we obtain
we obtain
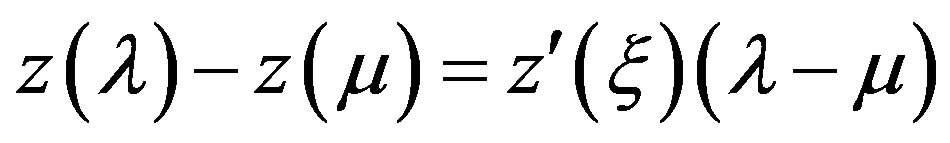 ,
,  whence it follows that the function
whence it follows that the function 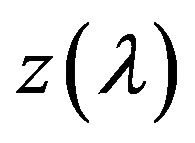 is an increasing one.
is an increasing one.
Consider now the behavior of function  in the neighborhood
in the neighborhood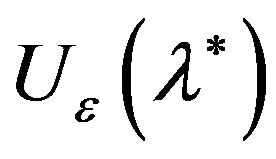 , taking into account its image (7). For any
, taking into account its image (7). For any 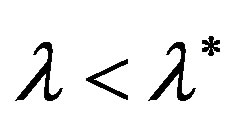 and
and 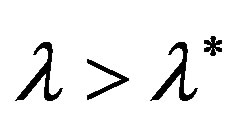 we obtain, respectively, the inequalities
we obtain, respectively, the inequalities
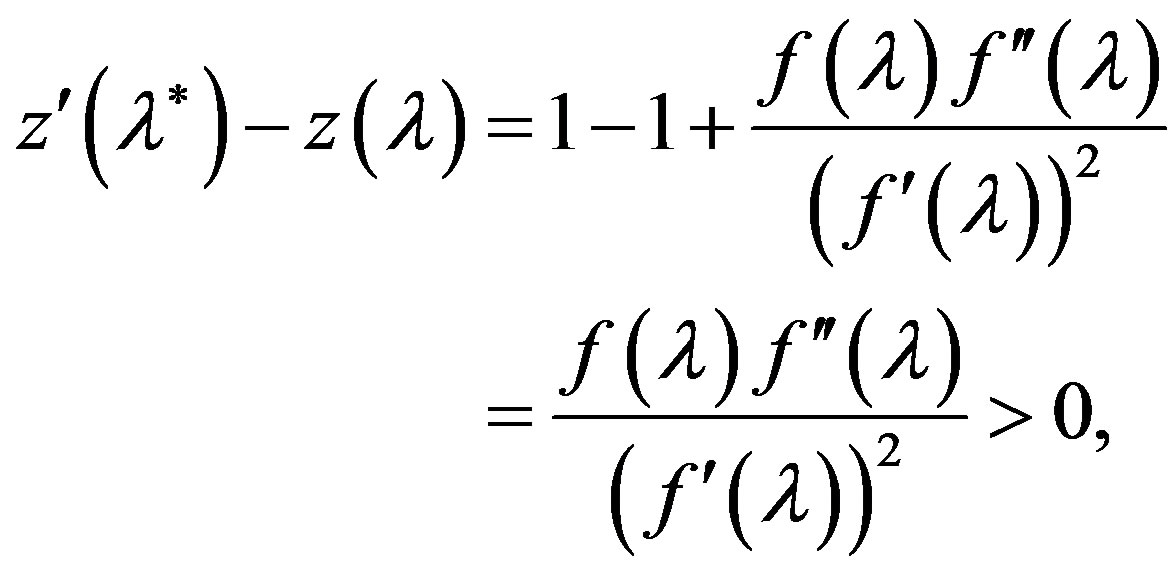 (8)
(8)
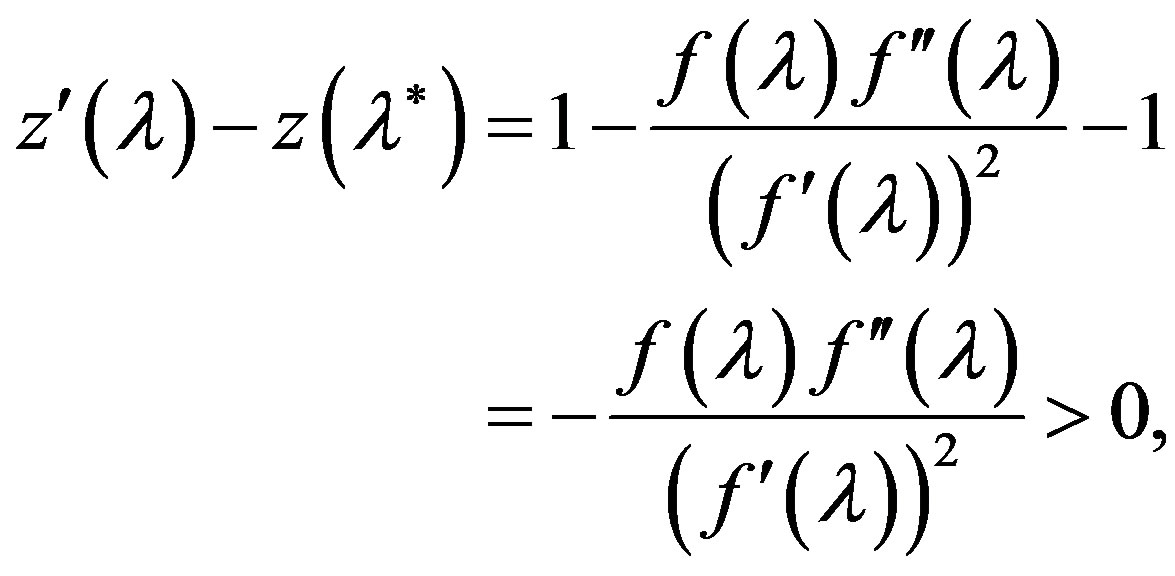
since 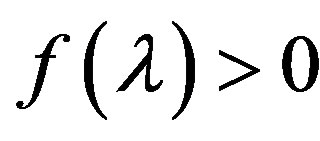 for
for 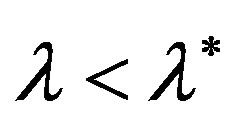 and for
and for 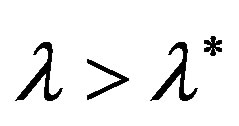
 . From the inequalities (8) it follows that in the neighborhood
. From the inequalities (8) it follows that in the neighborhood  the derivative
the derivative 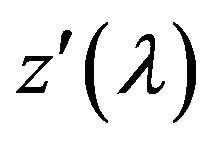 is increasing, and, consequently, the function
is increasing, and, consequently, the function 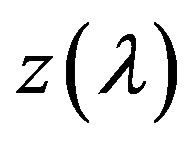 is convex in this neighborhood of the root.
is convex in this neighborhood of the root.
Similar statements about the function 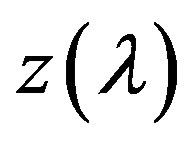 and its derivatives we obtain also for the cases (B), (C) and (D). But unlike the cases (A) and (D), in the cases (B) and (C) the function
and its derivatives we obtain also for the cases (B), (C) and (D). But unlike the cases (A) and (D), in the cases (B) and (C) the function 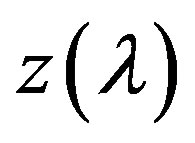 is concave. The theorem is proved.
is concave. The theorem is proved.
Thus, Theorem 3.1 determines the properties of function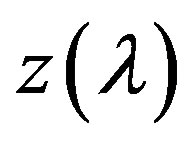 , and Figure 1 illustrates its behavior depends on the properties of function
, and Figure 1 illustrates its behavior depends on the properties of function  in some neighborhood of the root
in some neighborhood of the root .
.
4. Bilateral Analogues of Newton Method
Using the properties of functions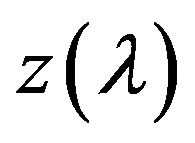 , we construct the sequence
, we construct the sequence 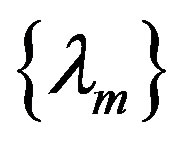 which has the property (3).
which has the property (3).
For the cases (A) and (D) iterative process can be rewritten in the form
 (9)
(9)
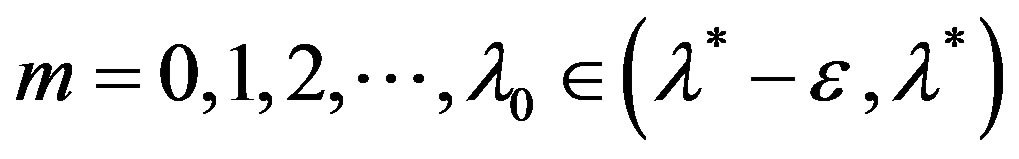 and for the cases (B) and (C) as
and for the cases (B) and (C) as
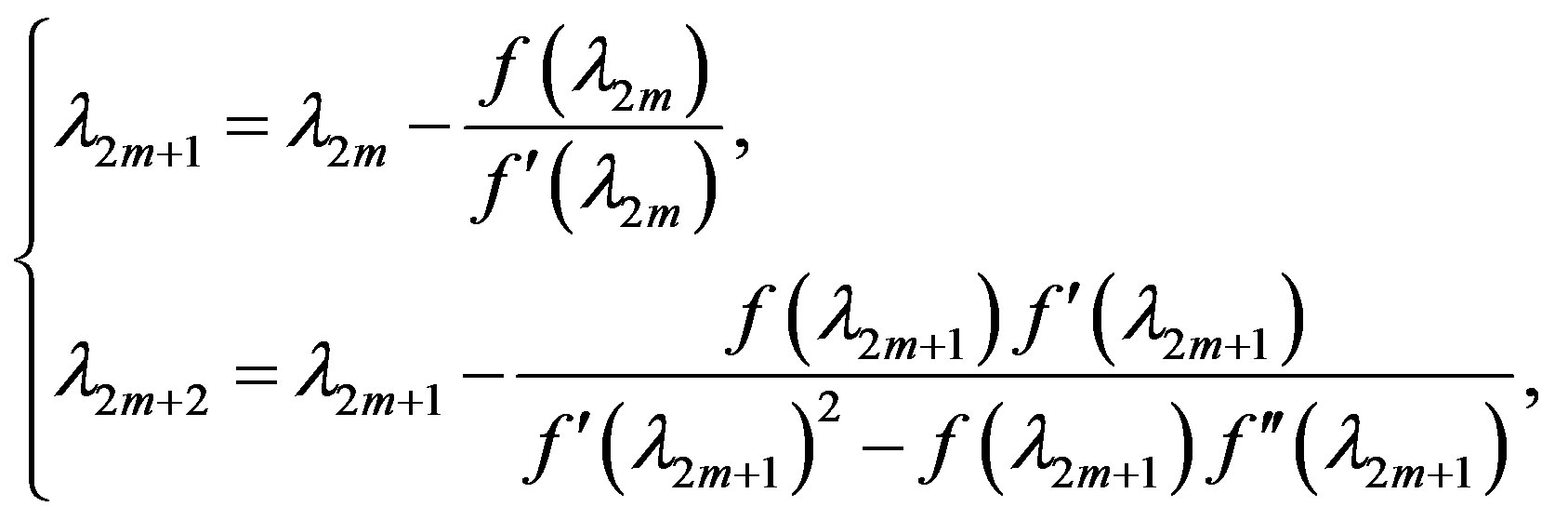 (10)
(10)
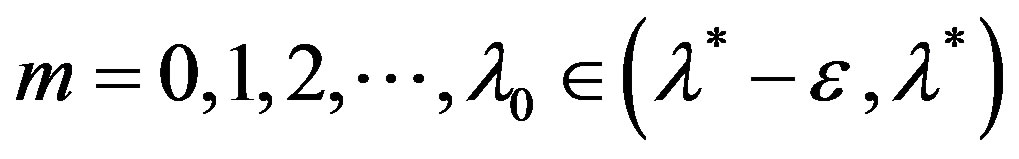 .
.
Justification of bilateral convergence of iterative processes provide the following theorems.
Theorem 4.1. Let  be a simple real root of equation (2) and let in some neighborhood of the root
be a simple real root of equation (2) and let in some neighborhood of the root
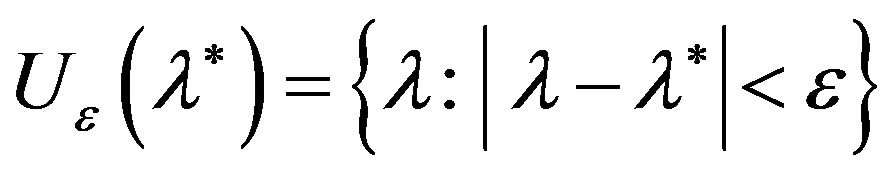 ,
,

Figure 1. Behavior of the functions f(λ) and z(λ) in the neighborhood of a simple real root λ* of functions f(λ).
in which
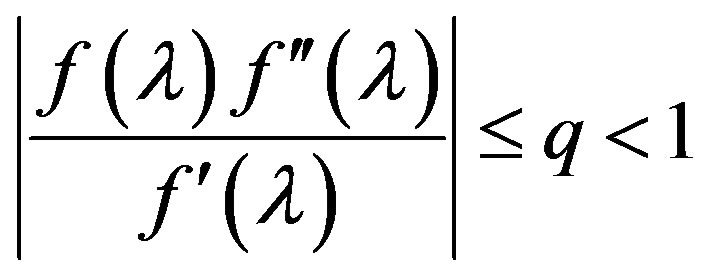
for three times continuously differentiable function 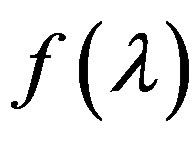 that describes the equation (2.2), the condition (A) or (D) be satisfied, and for the function
that describes the equation (2.2), the condition (A) or (D) be satisfied, and for the function 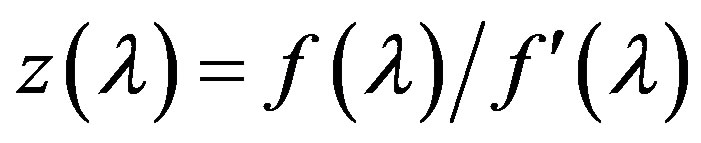 the inequalities
the inequalities
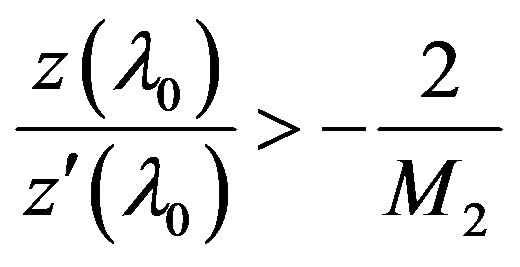 for
for ,
,
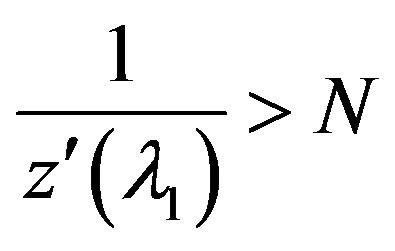 for
for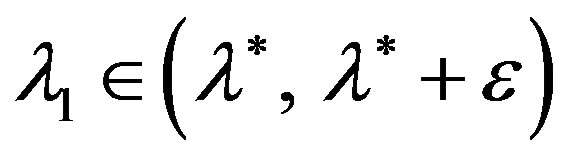 be satisfied, where
be satisfied, where
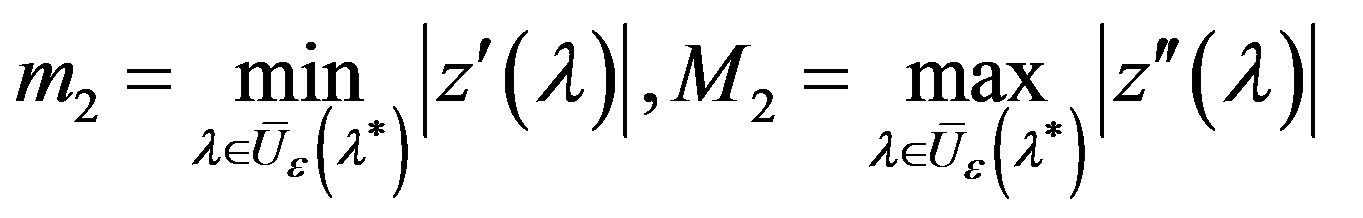 ,
,
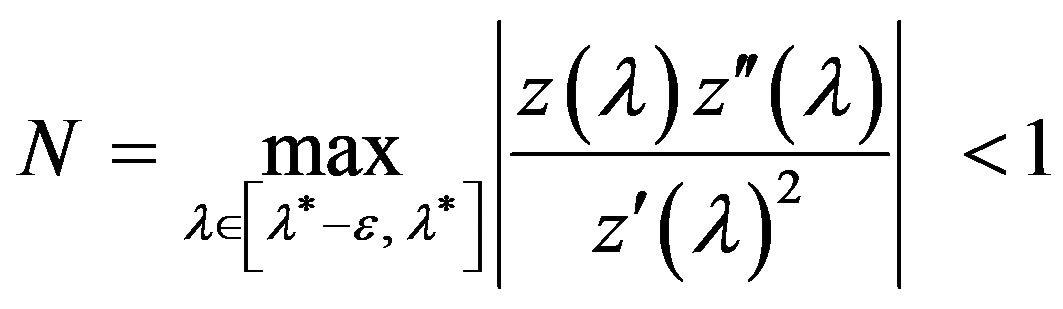
In addition, let the conditions
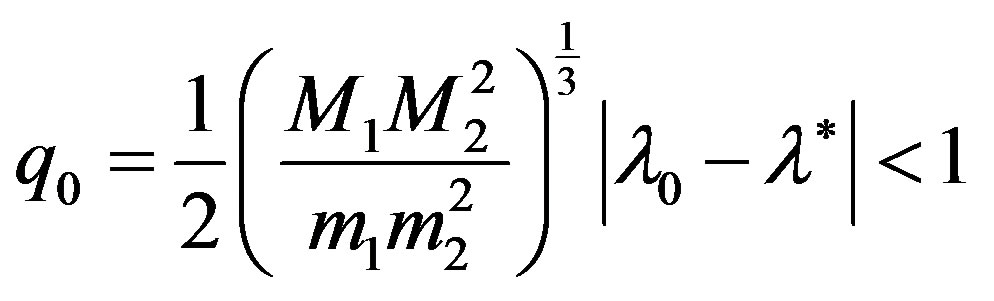 ,
,
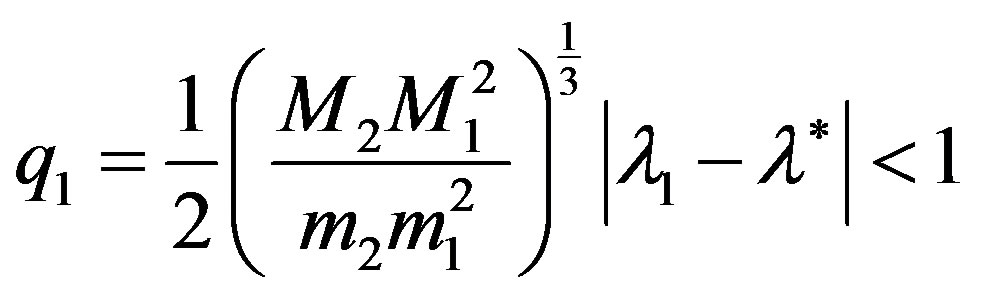
be satisfied, where
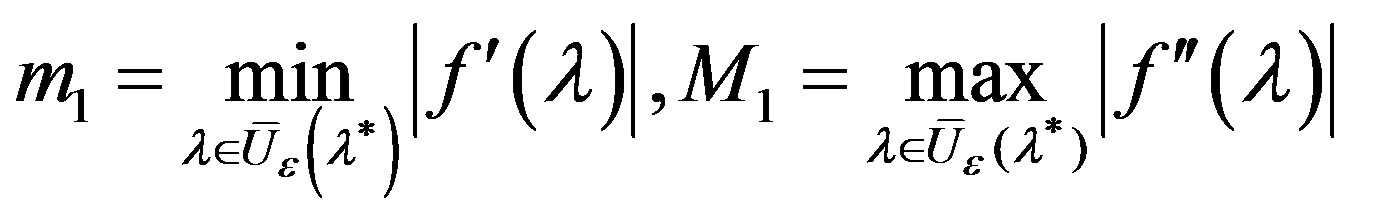 .
.
Then the iterative process (9), beginning with
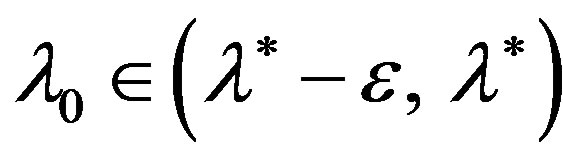 , convergence to solution
, convergence to solution 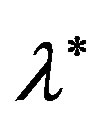 from both sides
from both sides
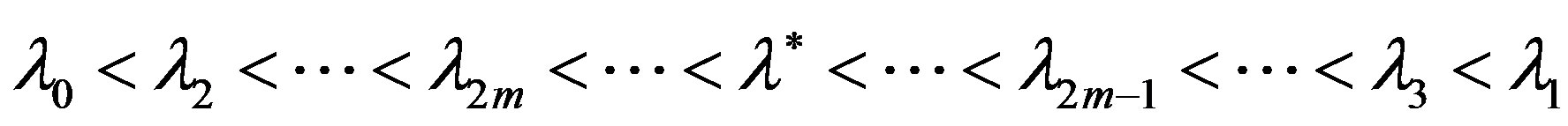 and for the errors from the left and from the right the estimations
and for the errors from the left and from the right the estimations
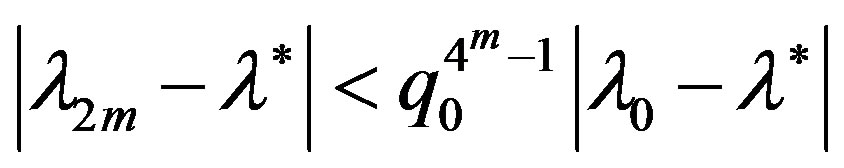 ,
,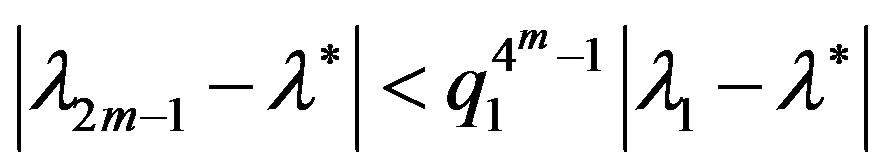 .
.
are fulfilled, respectively.
Theorem 4.2. Let 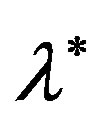 be a simple real root of equation (2) and let in some neighborhood of the root
be a simple real root of equation (2) and let in some neighborhood of the root
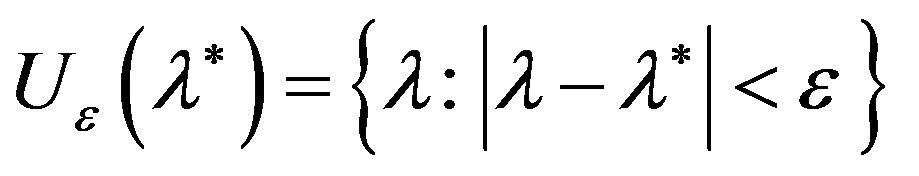 in which
in which
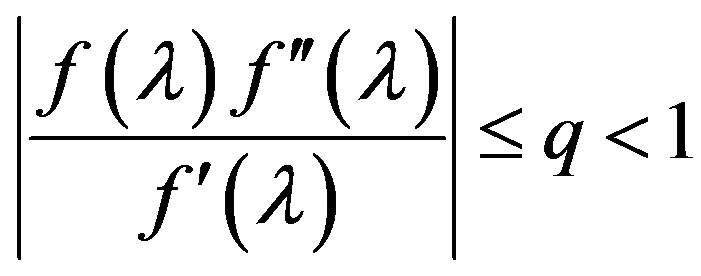
for three times continuously differentiable function 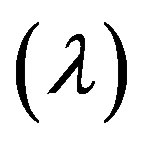 that describes the Equation (2), the condition (B) or (C) to be satisfied, and for the function
that describes the Equation (2), the condition (B) or (C) to be satisfied, and for the function 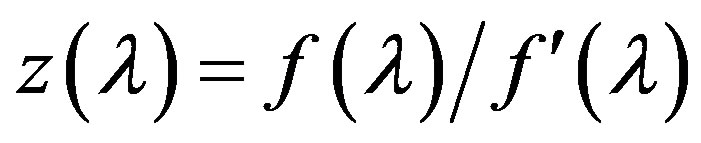 the inequalities
the inequalities
 for
for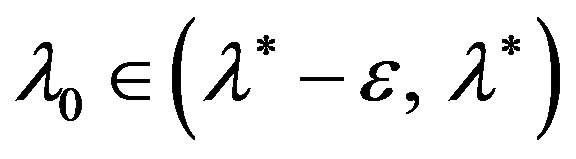 ,
,
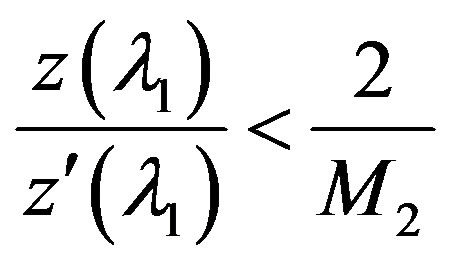 for
for 
be satisfied, where
 ,
,
 .
.
In addition, let the conditions
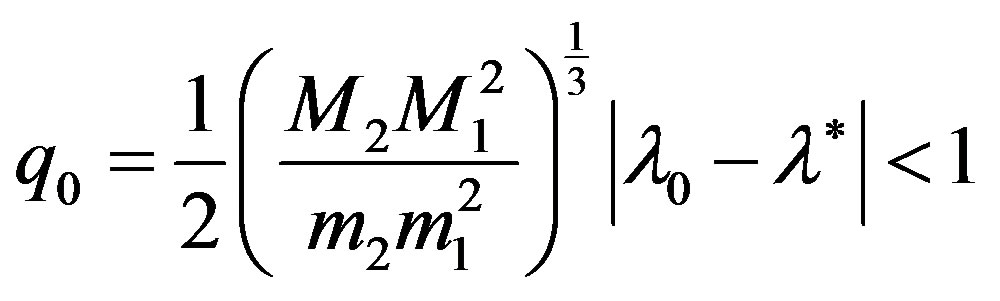 ,
,
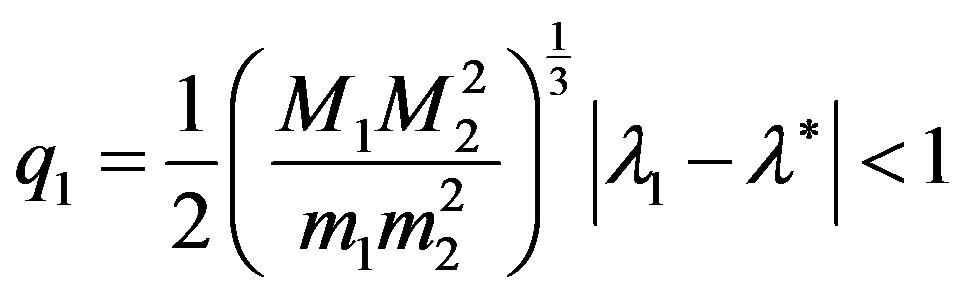
be satisfied, where
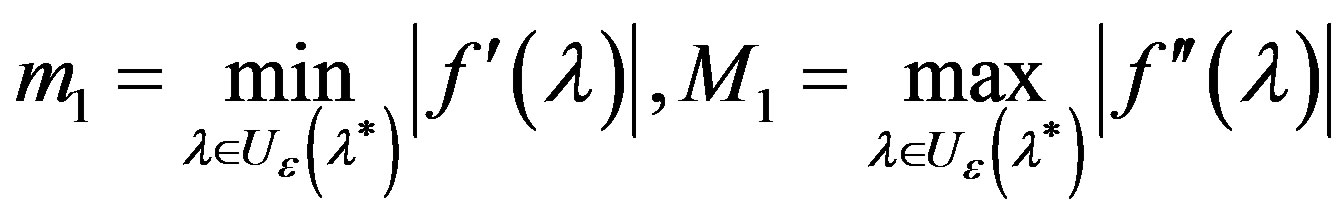
Then the iterative process (10), beginning with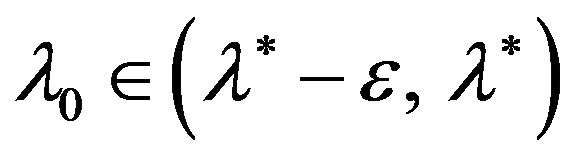 , convergence to the solution
, convergence to the solution 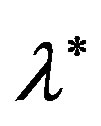 from both sides
from both sides
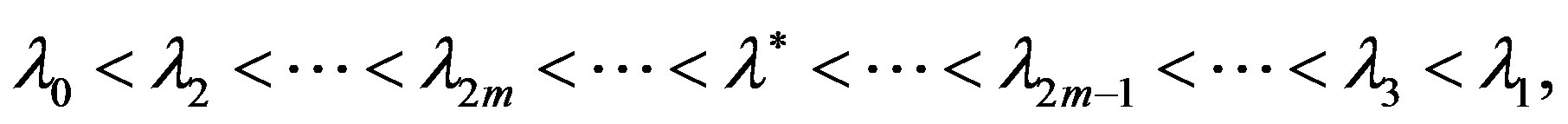
and for the errors from the left hand and from the right hand the estimation
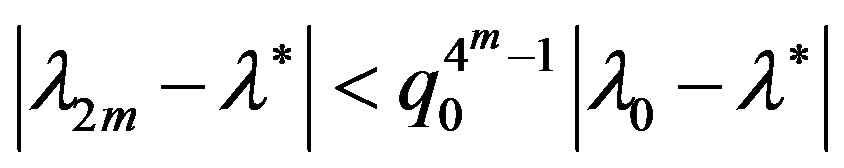 ,
,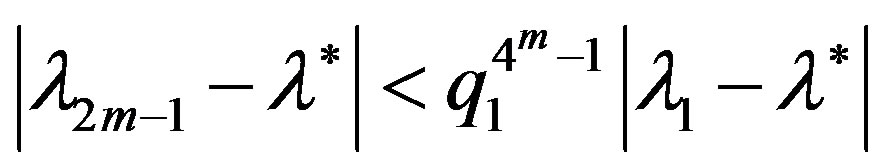 .
.
are fulfilled, respectively.
Remark. Two different iterative processes (9) and (10) were used above to justify the alternate approximation in the ideal case, when the behavior of functions 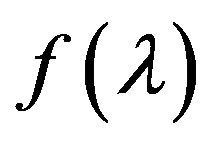 is known or easily investigates. Then alternate approximations come from
is known or easily investigates. Then alternate approximations come from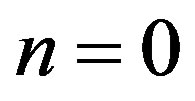 .
.
In practice, you can use any one of them for all cases (A)-(D) and regardless of which side (left or right from the root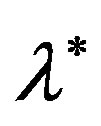 ) the initial approximation
) the initial approximation 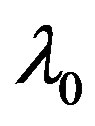 is and the algorithm adapts itself to bilateral approximations but then alternate approximations appear at least with
is and the algorithm adapts itself to bilateral approximations but then alternate approximations appear at least with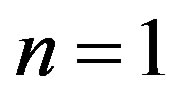 .
.
5. Algorithm of Alternate Approximations and Numerical Results
To test the proposed iterative processes consider the model eigenvalue problem with quadratic dependence on the parameter
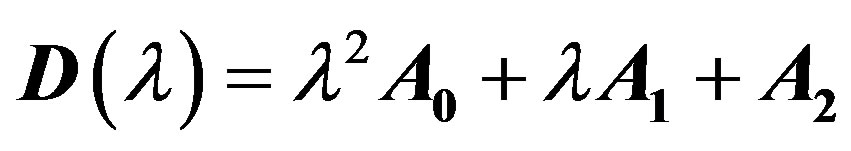 , (11)
, (11)
where
 ,
,
 ,
,
 .
.
The eigenvalues will be found as solutions of the determinant equation
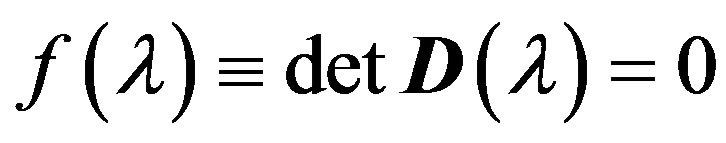 .
.
To this end we use the iterative process of alternate approximations (9), which is represented in equivalent form by replacing the function value and its derivatives at the required points by relations (6), which are obtained as a result of LU-decomposition of the matrix  (5). As a result, the iterative process (9) takes the form
(5). As a result, the iterative process (9) takes the form
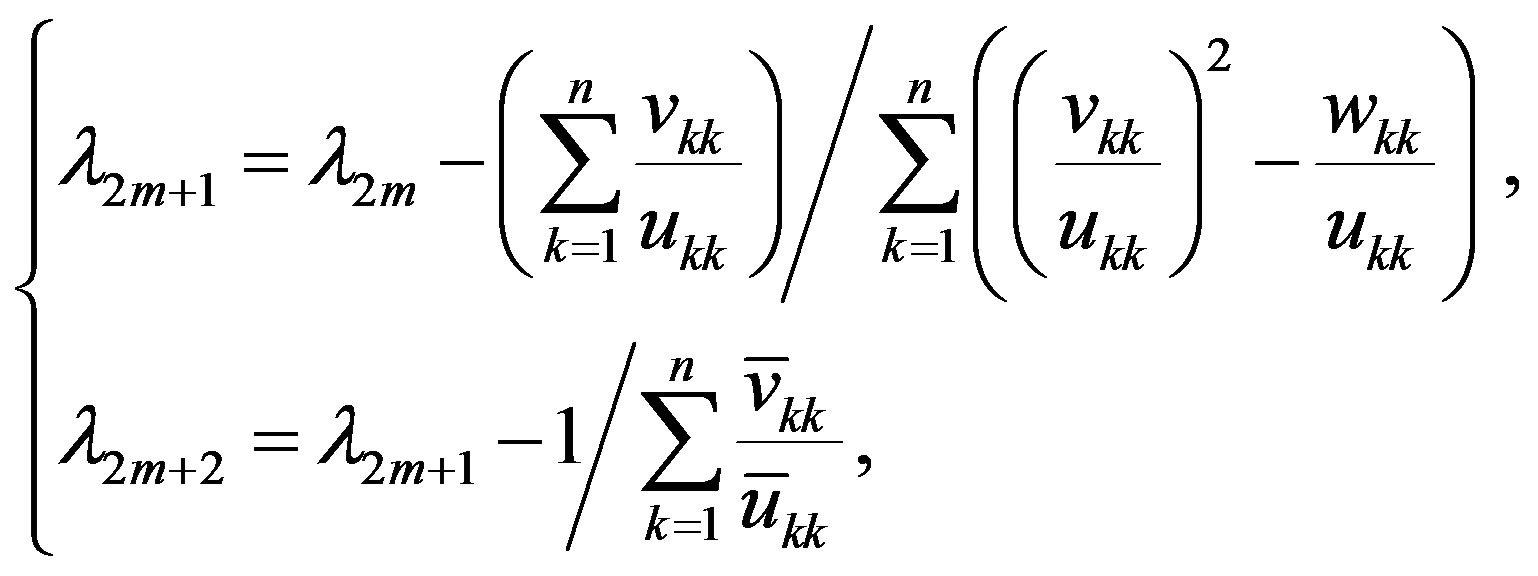 (12)
(12)
 where
where 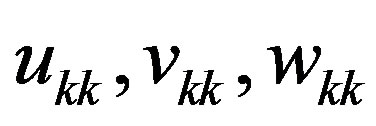 are the elements of matrix
are the elements of matrix 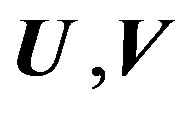 and
and 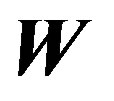 in the decompositions (5) at the fixed
in the decompositions (5) at the fixed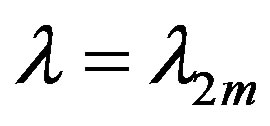 , and
, and 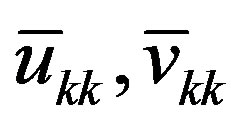 are the elements of matrix
are the elements of matrix 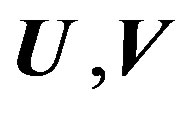 in this decompositions (5) at the fixed
in this decompositions (5) at the fixed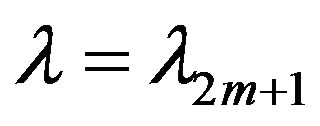 .
.
Thus, the algorithm can be written in the following.
Algorithm.
Step 1. Set the initial approximation  to the
to the 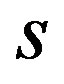 -th eigenvalue of the problem (2.15).
-th eigenvalue of the problem (2.15).
Step 2. for m = 0,1,2, ··· to achieve the accuracy do Step 3. if m is even.
Step 4. Compute the values 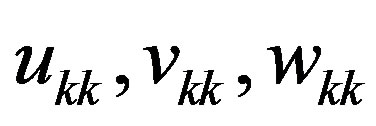 from the decompositions (5) at
from the decompositions (5) at .
.
Step 5. Compute the approximation to the eigenvalue  by (12).
by (12).
Step 6. go to step 10.
Step 7. if m is odd.
Step 8. Compute the values 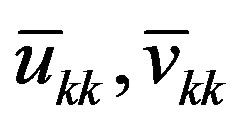 from the decompositions (5) at
from the decompositions (5) at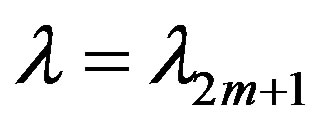 .
.
Step 9. Compute the approximation to the eigenvalue 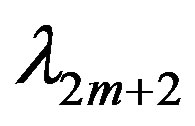 by (12).
by (12).
Step 10. end for m.
For numerous initial approximations all the eigenvalues of problem (11) were calculated. They fully coincide with the eigenvalues obtained by the usual Newton’s method. But the advantage of the algorithm is, in particular, that they give the bilateral approximations. It can be seen, having considered the Table 1 which shows the results of calculations for four eigenvalues. The first column shows the number of eigenvalue, the second shows the number of iterations, the third and fifth the obtained approximations are indicated, respectively, of the left hand and of the right hand, to the 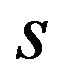 -th eigenvalue at each iteration, including the initial approximation. The value of the s-th eigenvalue is given in the fourth column. Calculations were carried out to within
-th eigenvalue at each iteration, including the initial approximation. The value of the s-th eigenvalue is given in the fourth column. Calculations were carried out to within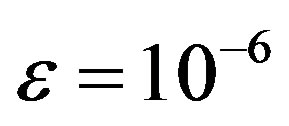 .
.
The table shows that for the 1st and 2nd eigenvalues for the iterative process we obtain bilateral alternating approximations of the form
 and for the 7th eigenvalue of the form
and for the 7th eigenvalue of the form
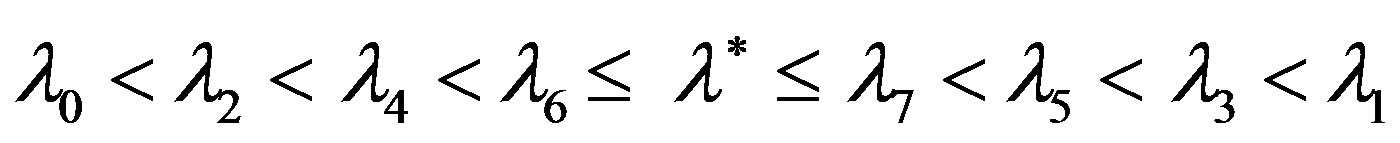 beginning with
beginning with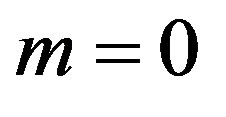 . For the 8th eigenvalue we have obtained the also bilateral approximations similar as for the 7th one, but the alternating approximations come from
. For the 8th eigenvalue we have obtained the also bilateral approximations similar as for the 7th one, but the alternating approximations come from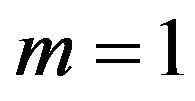 , i.e.
, i.e.
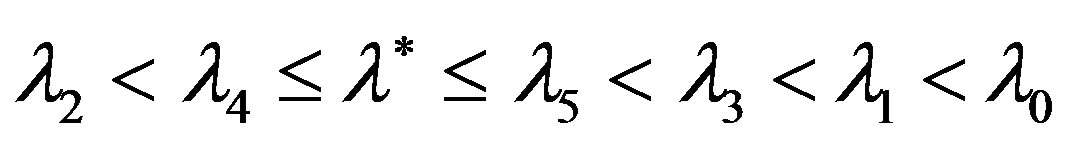 .
.
6. Conclusions
Approbation of constructed algorithms on model problems shows their reliability and efficiency, and also advantages in comparison with the usual Newton’s method in the sense that at every step of iterative process we obtain two-sided estimates of the desired solution, and hence at each step we obtain comfortable a posteriori error estimates .
The proposed approach can be applied to the linear eigenvalue problems with respect to the spectral parameter, moreover if it is compared with existing approaches for obtaining lower bounds of eigenvalues of self-adjoint spectral problems, the approach in contrast to:
Ÿ the methods based on inclusion theorems (Temple, Krylov-Bogolyubov), does not require knowledge of the lower border of the following eigenvalue (assuming that the eigenvalues are arranged in ascending order)Ÿ the method of intermediate problems and its various modifications does not require construction of a basic operator with known eigenvalues so that the differ-

Table 1. Bilateral approximations of the eigenvalues of the problem (11).
ence between self-adjoint operator of the original problem and the base one was a positive operator, and constraction of finite-dimentional perturbation of basic operator Ÿ Fikera method and its modifications, does not require that the inverse to the original operator was compact operator and its construction.
REFERENCES
- G. Temple, “The theory of Rayleigh’s principle as applied to Continuous Systems,” Proceedings of the Royal Society A, Vol. 119, No. 782, 1928, pp. 276-293. doi:10.1098/rspa.1928.0098
- L. Collatz, “Eigenwertaufgaben mit technischen Anwendungen,” Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig, 1963.
- N. J. Lehmann, “Beitrage zur Losung linearer Eigenwertpromleme I,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 29, 1949, pp. 341-356.
- N. J. Lehmann, “Beitrage zur Losung linearer Eigenwertpromleme II,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 30, No. 1-2, 1950, pp. 1-16. doi:10.1002/zamm.19500300101
- A. V. Knyazev, “A Block Algorithm for the Kato-Temple estimates for the Eigenvalues: Rationale and application,” In: V. V. Voevodin, Ed., Adjoint equations and perturbation theory in Mathematical Physics, in Russian, DCM AS USSR, Moscow, 1985, pp. 127-135.
- A. V. Knyazev, V. I. Lebedev and A. L. Skorokhodov, “Temple-Lehmann methods in Iterative Algorithms,” in Russian, DCM AS USSR, Moscow, 1985.
- B. N. Parlett, “The Symmetric Eignvalue Problem,” Prentice Hall, Englewood Clifs, 1980.
- H. Behnke and F. Goerisch, “Inclusions for eigenvalues of Selfadjoint Problems,” In: J. Herzberger, Ed., Topics in Validated Computations, Elsevier, Amsterdam, 1994, pp. 277-322.
- H. Behnke, “The calculation of Guarateed Bounds for Eigenvalues Using Complementary Variational Principles,” Computing, Vol. 47, No. 1, 1991, pp. 11-27. doi:10.1007/BF02242019
- M. G. Marmorino and R. W. Bauernfeind, “Approximate Lower Bound of the Weinstein and Temple variety,” International Journal of Quantum Chemistry, Vol. 107, No. 6, 2007, pp. 1405-1414. doi:10.1002/qua.21268
- A. Weinstein and W. Stenger, “Methods of Intermediate Problems for eigenvalues. Theory and ramifications,” Academic Press, New York, 1972.
- N. W. Bazley and D. W. Fox, “Truncations in the method of Intermediate Problems for Lower Bounds to eigenvalues,” Journal of Research of the National Bureau of Standards Section B, Vol. 65, No. 2, 1961, pp. 105-111.
- C. A. Beattie, “An extension of Aronszajn’s rule; slicing the spectrum for Intermediate Problems,” SIAM Journal on Numerical Analysis, Vol. 24, No. 4, 1987, pp. 828-843. doi:10.1137/0724053
- C. A. Beattie and W. M. Greenlee, “Convergence theorems for Intermediate Problems. II,” Proceedings of the Royal Society of Edinburgh: Section A, Vol. 132, No. 5, 2002, pp. 1057-1072.
- S. H. Gould, “Variational Methods for Eigenvalue Problems,” Oxford University Press, London, 1966.
- G. Fichera, “Numerical and Quantitative Analysis,” Pitnam Press, London, 1978.
- B. M. Podlevskyi, “On One Approach to Building Bilateral Iterative Methods for Solving Nonlinear Equations,” in Ukraine, Report NAS of Ukraine, No. 5, 1998, pp. 37-41.
- B. M. Podlevskyi, “About One Way to Build Bilateral Iterative Methods for Solving Nonlinear Equations,” in Ukraine, Physicomechanical Fields, Vol. 42, No. 2, 1999, pp. 17-25.
- B. M. Podlevskyi, “One approach to the construction of the Bilateral Approximations Methods for the solution of Nonlinear Equations,” In: G. S. Ladde, N. G. Madhin and M. Sambandham, Eds., Proceeding of Dynamic Systems & Applications IV, Dynamic Publishers Inc., Atlanta, 2004, pp. 542-547.
- G. Alefeld and J. Herzberger, “Introduction to Interval Computations,” Academic Press, New York, 1983.
- A. Neumaier, “Interval methods for systems of equations,” Cambridge University Press, Cambridge, 1990.
- B. M. Podlevskyi, “Numerical methods and algorithms for Solving Generalized Spectral Problems,” Ph.D. Thesis, Institute of Mathematics of NASU, Kyiv, 2011.
- B. M. Podlevskyi, “On Certain Two-Sided Analogues of Newton’s Method for Solving Nonlinear Eigenvalue Problems,” Computational Mathematics and Mathematical Physics, Vol. 47, No. 11, 2007, pp. 1745-1755. doi:10.1134/S0965542507110024
- Z. Bohte, “Numerical solution of Some Two-Parameter Eigenvalue Problems,” In: P. Gosar and L. Suklje, Eds., Spominski Zbornik Antona Kuhlja, Slovenian Academy of Science and Art, Ljubljana, 1982, pp. 17-28.

