American Journal of Computational Mathematics
Vol.2 No.1(2012), Article ID:17969,4 pages DOI:10.4236/ajcm.2012.21008
Examination of a Special Function Defined by an Integral
Department of Mechanical Engineering, Yildiz Technical University, Istanbul, Turkey
Email: hversoy@yildiz.edu.tr
Received September 14, 2011; revised October 3, 2011; accepted October 15, 2011
Keywords: Special Function; Complementary Error Function; Gamma Function
ABSTRACT
The aim of this short note is to examine the properties of a special function defined by an integral which was appeared in a paper by Ersoy. It is revealed that the function 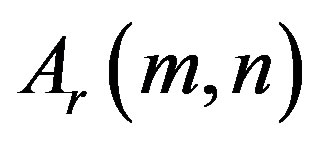 for
for  is expressed in terms of the gamma function and it varies linearly with
is expressed in terms of the gamma function and it varies linearly with 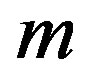 for
for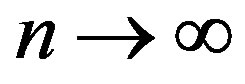 . Its appropriate graphs are plotted and its pertinent values are tabulated.
. Its appropriate graphs are plotted and its pertinent values are tabulated.
1. Introduction
Ersoy [1] obtained a series solution which is rapidly convergent at small times while he investigated an expression for velocity field of an unsteady flow between eccentric rotating disks. In this short note, the properties of the special function used in the series solution are presented.
2. Definition of the Function 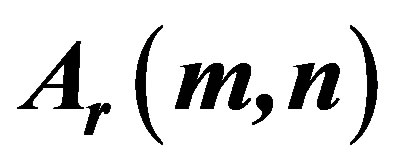
The function  is defined as follows:
is defined as follows:
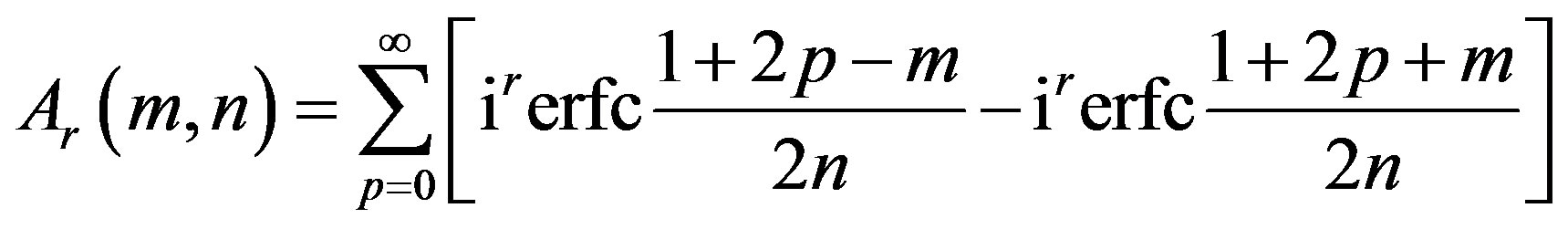 (1)
(1)
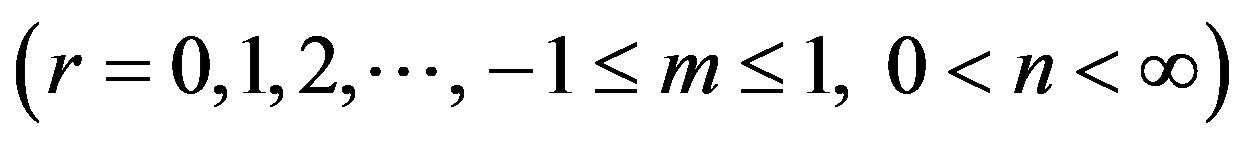
where
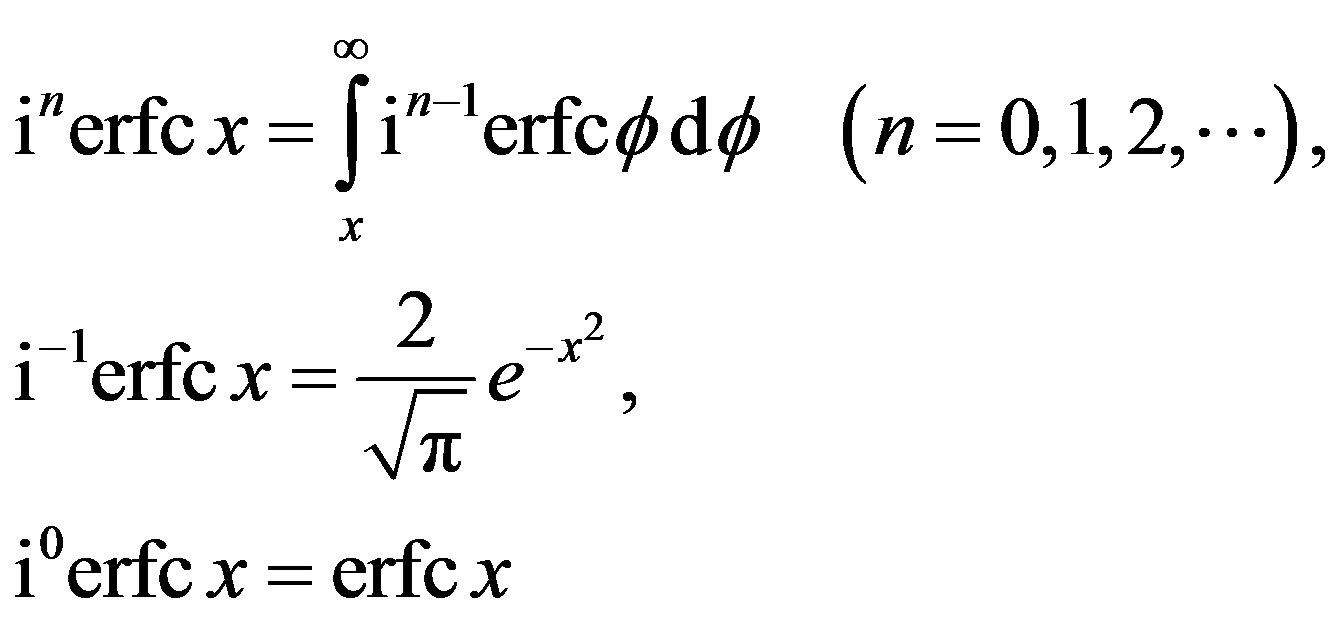 (2)
(2)
 and
and  denote the complementary error function and the repeated integrals of the complementary error function, respectively [2].
denote the complementary error function and the repeated integrals of the complementary error function, respectively [2].
3. Main Results
In order to acquire the properties of the function , computer-assisted research is done. Furthermore, the illustrative graphs are shown in Figures 1-6 and the elucidative values are provided in Tables 1-7. The results are noted as follows:
, computer-assisted research is done. Furthermore, the illustrative graphs are shown in Figures 1-6 and the elucidative values are provided in Tables 1-7. The results are noted as follows:
Ÿ The function 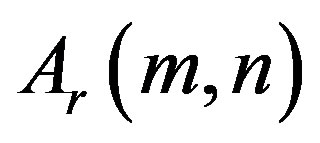 that is a continuous function is an odd function of
that is a continuous function is an odd function of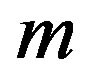 , i.e.,
, i.e.,
 .
.
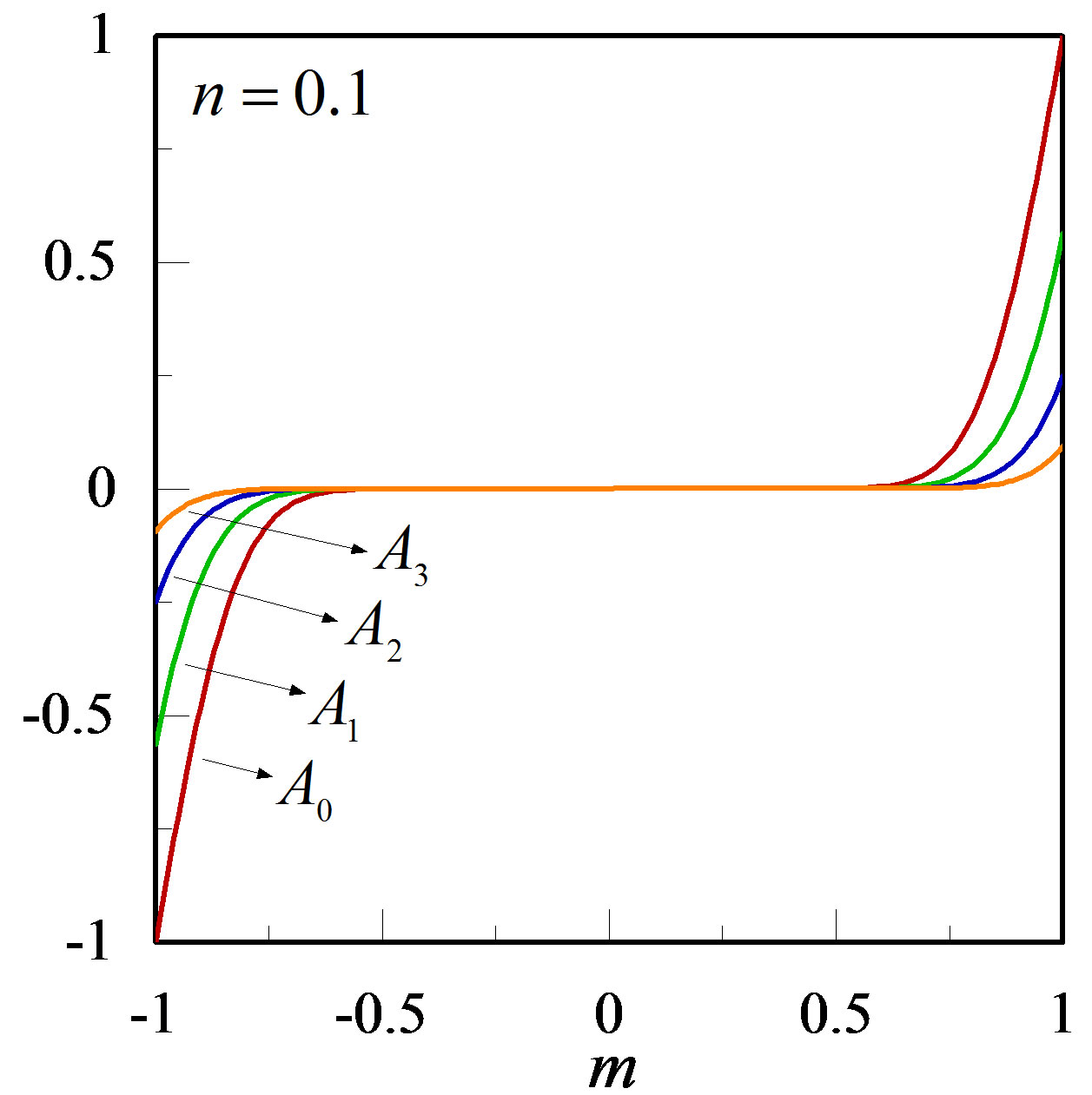
Figure 1. Variation of  with m (n = 0.1, r = 0, 1, 2, 3).
with m (n = 0.1, r = 0, 1, 2, 3).

Figure 2. Variation of  with m (n = 0.1, r = 4, 5, 6).
with m (n = 0.1, r = 4, 5, 6).
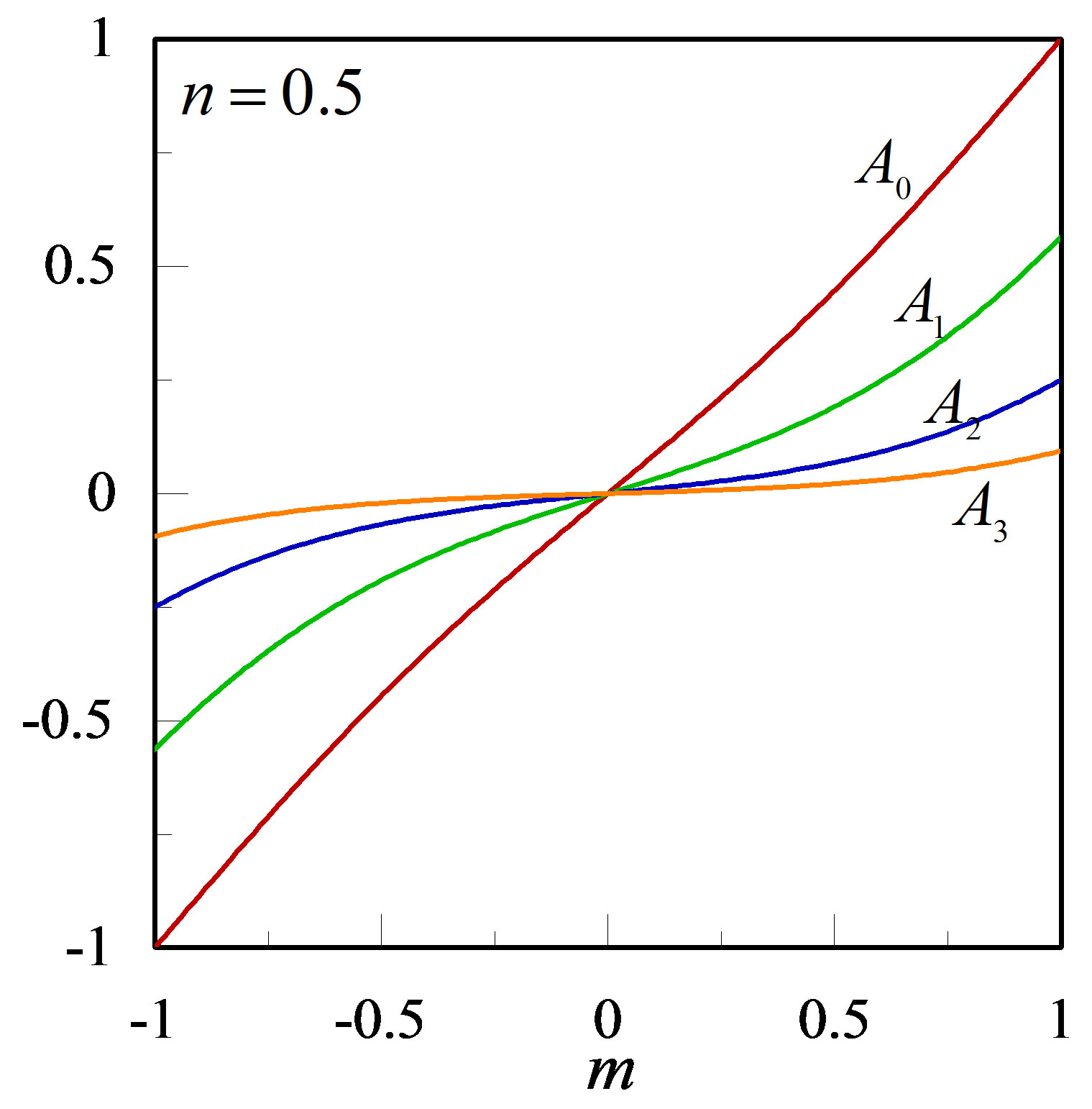
Figure 3. Variation of 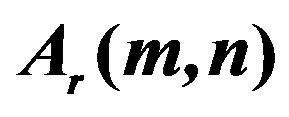 with m (n = 0.5, r = 0, 1, 2, 3).
with m (n = 0.5, r = 0, 1, 2, 3).

Figure 4. Variation of  with m (n = 0.5, r = 4, 5, 6).
with m (n = 0.5, r = 4, 5, 6).

Figure 5. Variation of 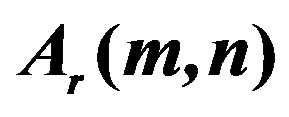 with m (n = 1, r = 0, 1, 2, 3).
with m (n = 1, r = 0, 1, 2, 3).

Figure 6. Variation of 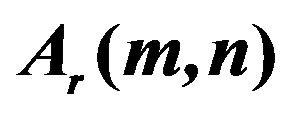 with m (n = 1, r = 4, 5, 6).
with m (n = 1, r = 4, 5, 6).

Table 1. Some pertinent values of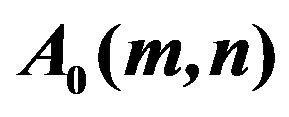 .
.
It becomes zero for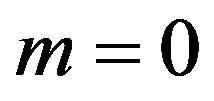 , i.e.,
, i.e.,
 .
.
Ÿ The function 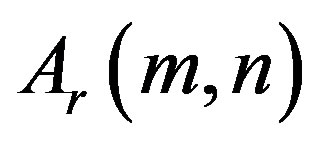 has the following relation for fixed
has the following relation for fixed  and
and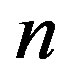 :
:
Ÿ 
Ÿ The function 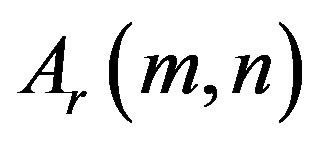 increases with
increases with  for fixed
for fixed

Table 2. Some pertinent values of .
.

Table 3. Some pertinent values of .
.
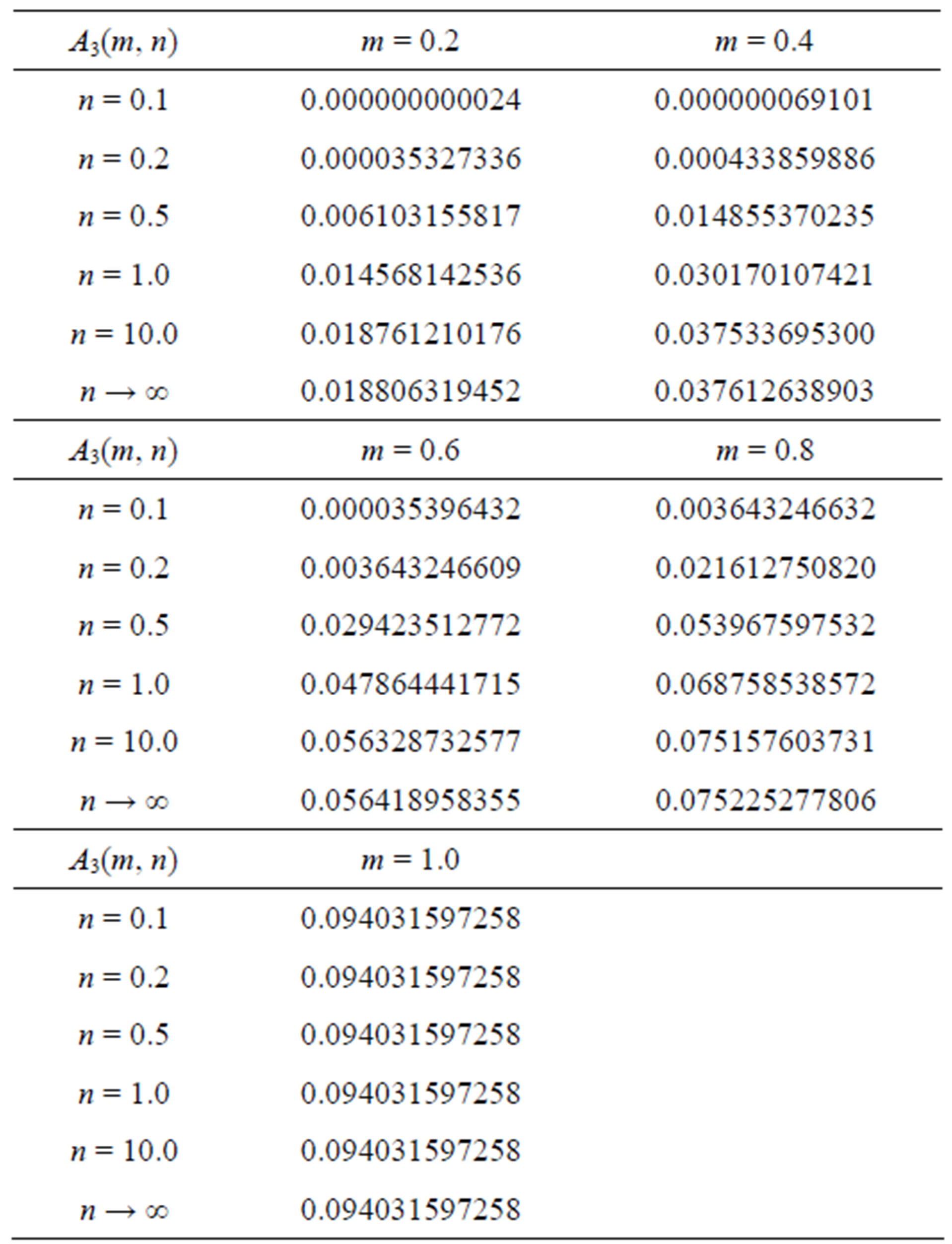
Table 4. Some pertinent values of .
.
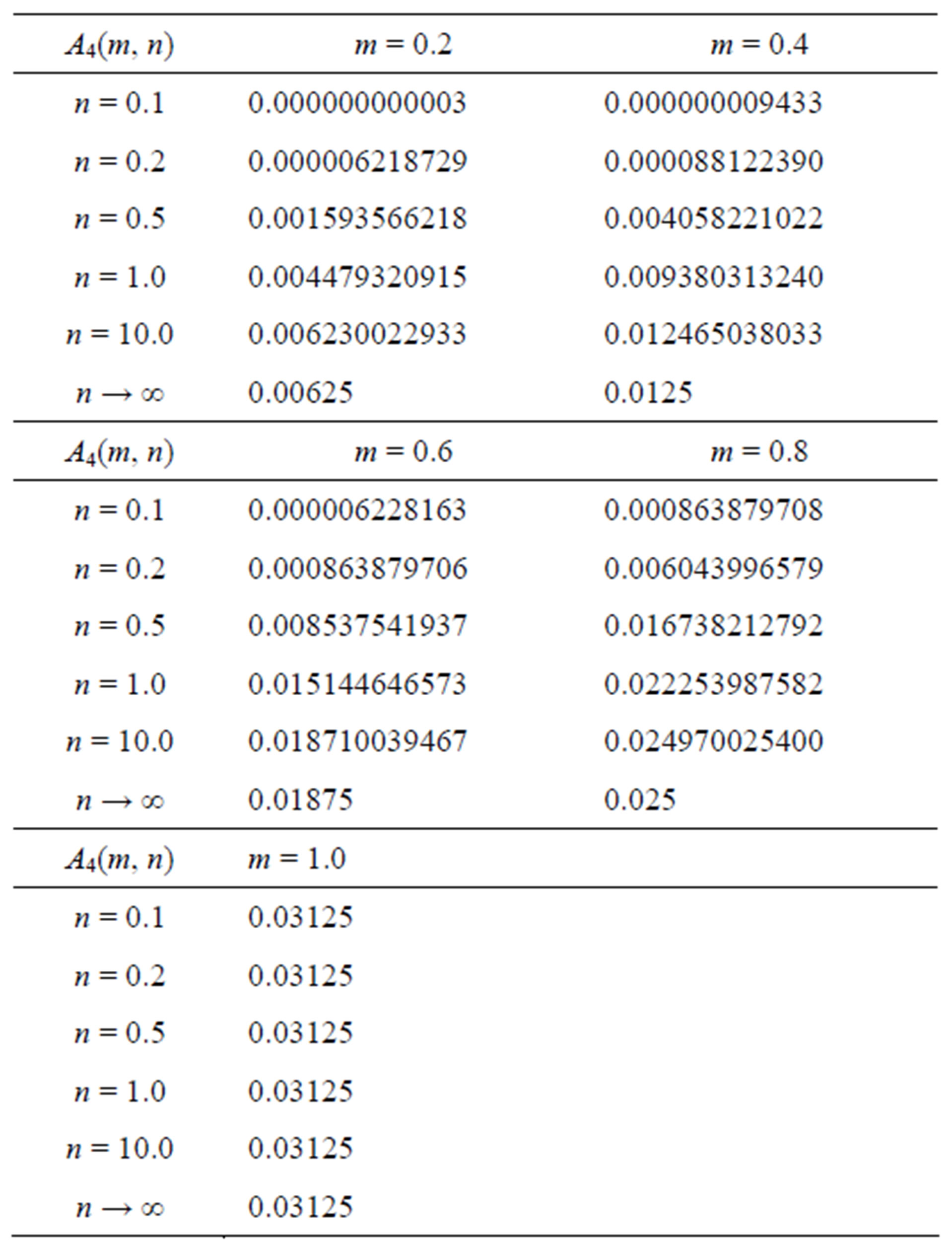
Table 5. Some pertinent values of .
.
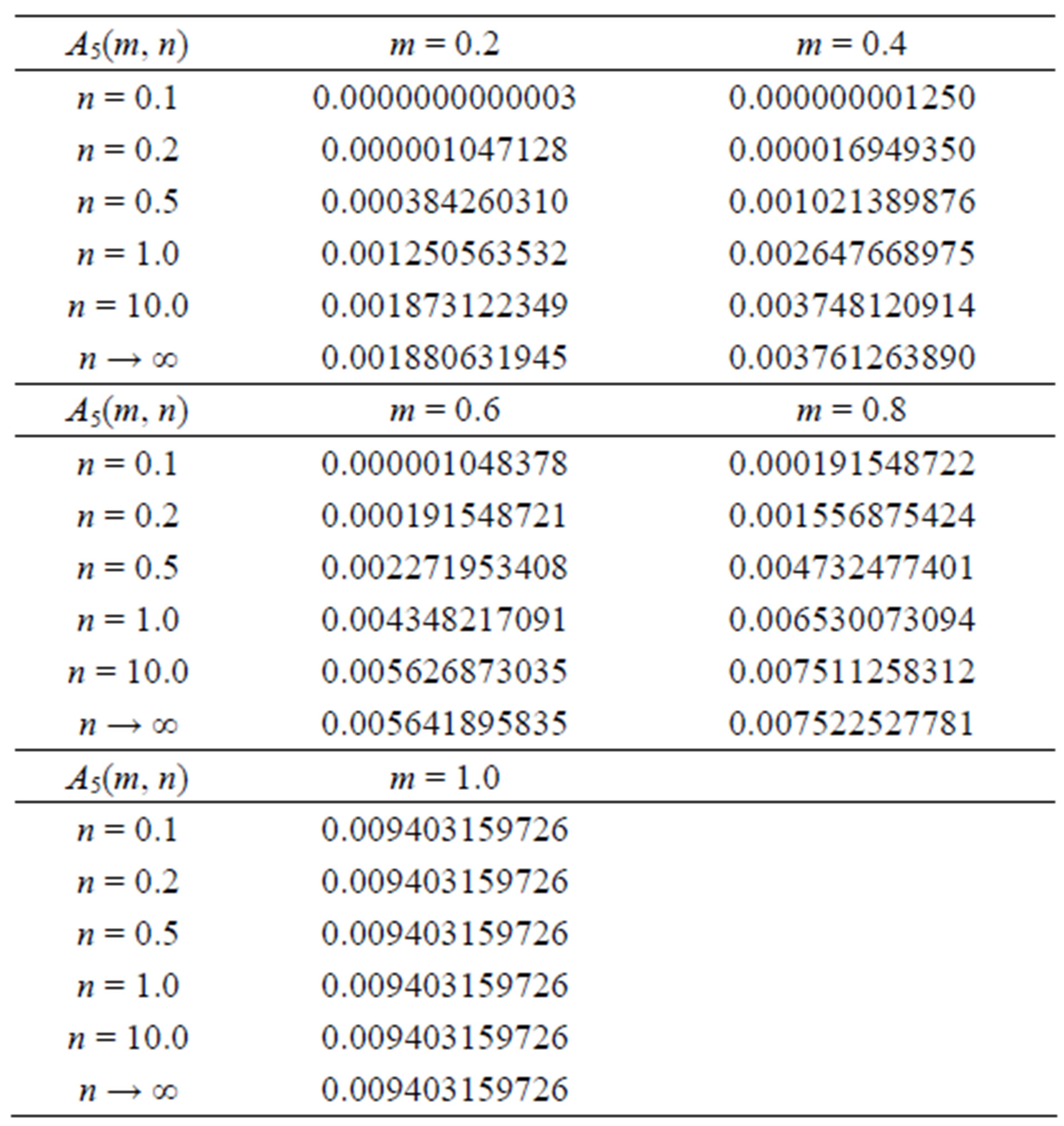
Table 6. Some pertinent values of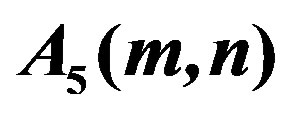 .
.
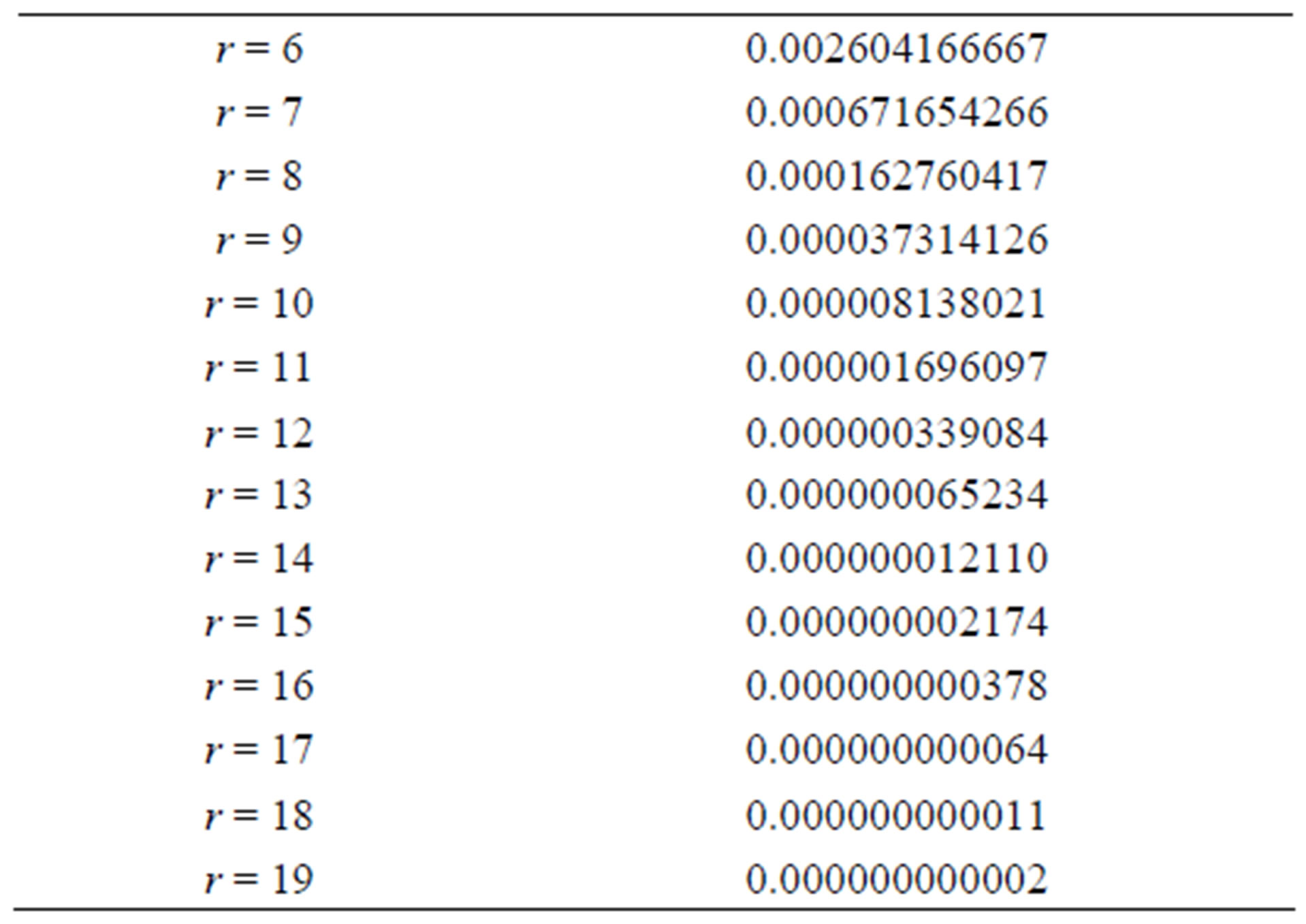
Table 7. Values of Ar(1, n) for r = 6 - 19.
n, i.e.Ÿ 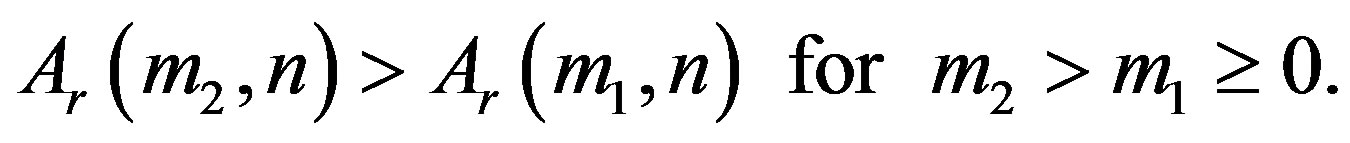
Ÿ The functions have maximum values for . Moreover, they have the same values for
. Moreover, they have the same values for  and any value of
and any value of . These values are as follows:
. These values are as follows:

or
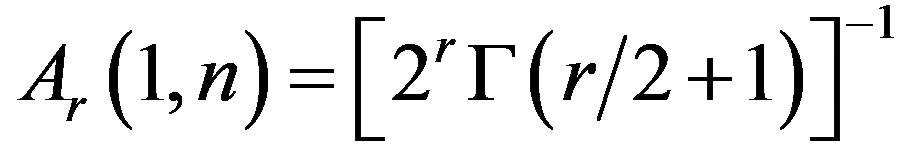
where 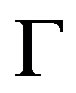 is the gamma function.
is the gamma function.
Ÿ When 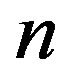 is larger, the function
is larger, the function  is also larger for any fixed value of
is also larger for any fixed value of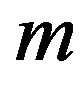 , i.e.,
, i.e.,
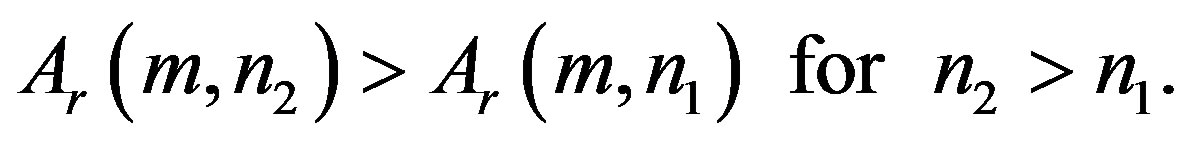
For large values of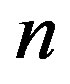 , it approximately varies linearly with
, it approximately varies linearly with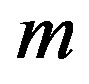 , i.e.,
, i.e.,
 .
.
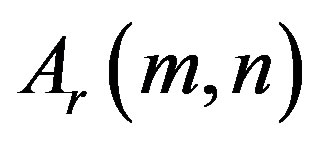 is more linear than
is more linear than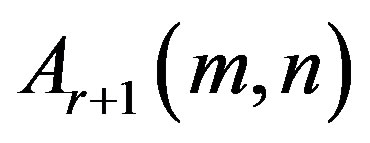 .
.
Ÿ For , it is a linear function of
, it is a linear function of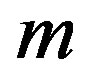 , i.e.,
, i.e.,
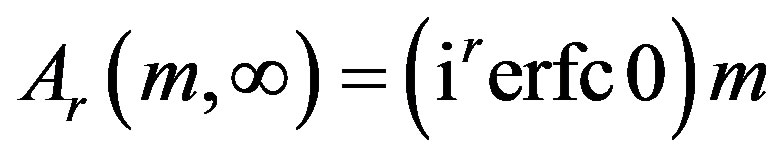 .
.
REFERENCES
- H. V. Ersoy, “Unsteady Flow Due to a Sudden Pull of Eccentric Rotating Disks,” International Journal of Engineering Science, Vol. 39, No. 3, 2001, pp. 343-354. doi:10.1016/S0020-7225(00)00040-9
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions,” Dover Publications, New York, 1972.

